人们每天都在行走，排除以运动健身为目的的走路方式，而仅仅考虑距离固定，以节省体力为最终目的的行走，那么选择多大的步长才最省力？

人在走路时所做的功等于抬高人体重心所需的势能与两腿运动所需的动能之和。在给定速度时，可以以单位时间内做功最小，即消耗能量最小为目标建立优化模型，并且确定出最优的走路步长。

人体分为躯体和下肢两部分，假设躯体以匀速前进，而把下肢看作长度固定的刚体棒。

Δ：人每走一步时，躯体重心移动的垂直距离。

θ：两脚着地时与竖直方向的夹角。

m：人体的质量，常量。

m'：人行走时产生动能的“折合质量”，常量。

s：人行走时的固定步长。

n：人在单位时间内行走的步数。

v：人走路的速度（匀速），常量。

l：人的腿长，常量。

Ep：表示单位时间内消耗的势能。

Ek：表示单位时间内消耗的动能。

g：表示重力加速度，常量。 

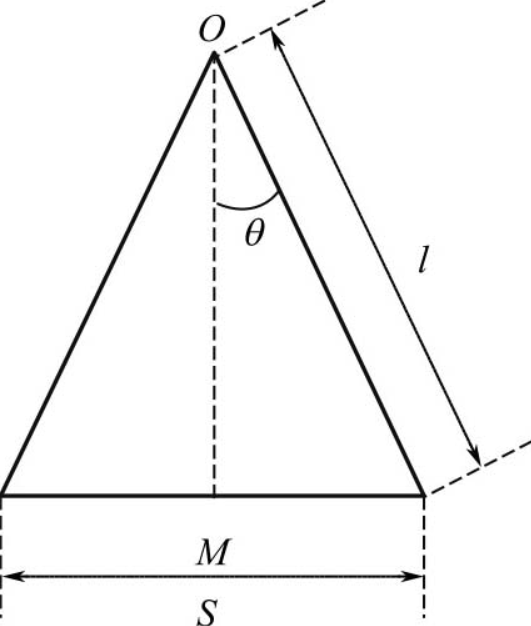
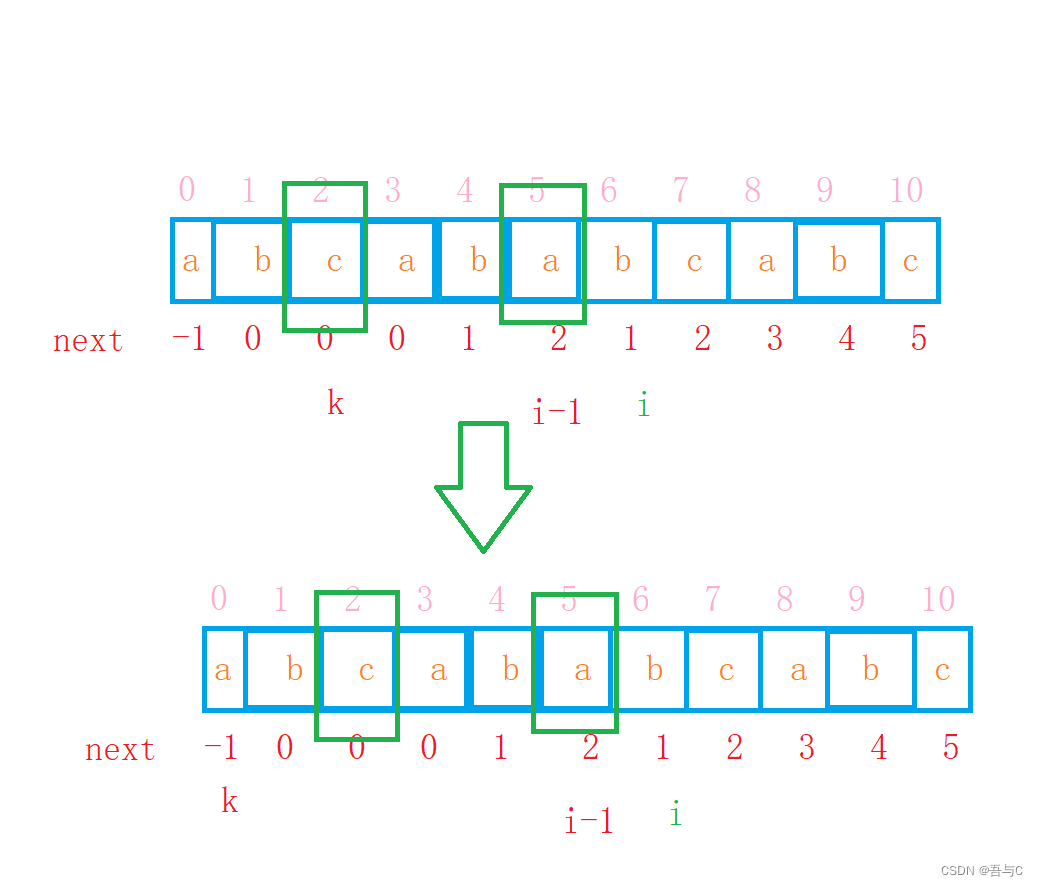
 如图所示，可知给定l和θ后，一个人每走一步其躯体重心移动的垂直距离为

Δ=l-OM=l-lcosθ=l（1-cosθ）

而人行走时的固定步长s=2lsinθ，故可得人行走的速度为v=ns。

而人行走时的固定步长s=2lsinθ，故可得人行走的速度为v=ns。

另一方面，人在走路时，腿的速度不断变化，动能消耗应与v2成正比，所以总的动能消耗为

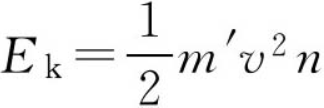
 其中折合质量m'的数值可以通过实验测出，在实际应用时可以近似成每条腿的质量。将前面结果代入后有

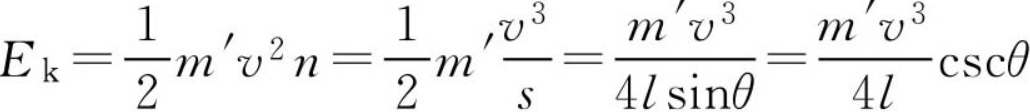
则

 求导

化简

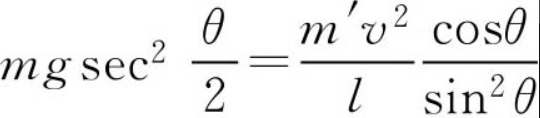
根据三角公式

得

故可得人行走时的最优步长为 

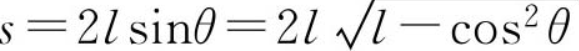
假设某人质量为m=65kg，腿长为l=1m，一条腿的质量为m'=12kg，走路的速度v=1.5m/s，运用上述模型则有

此时的最优行走步长为 

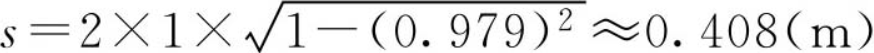
一秒钟内行走的步数为 

 

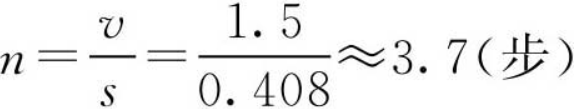
 可以看出所得结果基本上是符合实际情况的。