文章目录
- 静态的玫瑰
敲了这么多年代码,每年都得画一些心啊花啊什么的,所以现在常规的已经有些倦怠了,至少也得来个三维图形才看着比较合理,而且光是三维的也没啥意思,最好再加上能动起来。
静态的玫瑰
网上有很多生成玫瑰花的代码,比如下面这个
from matplotlib import cm
import matplotlib.pyplot as plt
import numpy as np
[x,t]=np.meshgrid(np.arange(25)/24.0,
np.arange(0,575.5,0.5)/575*17*np.pi-2*np.pi)
p=(np.pi/2)*np.exp(-t/(8*np.pi))
u=1-(1-np.mod(3.6*t,2*np.pi)/np.pi)**4/2
y=2*(x**2-x)**2*np.sin(p)
r=u*(x*np.sin(p)+y*np.cos(p))
X,Y = r*np.cos(t), r*np.sin(t)
Z = u*(x*np.cos(p)-y*np.sin(p))
ax=plt.subplot(projection='3d')
ax.plot_surface(X, Y, Z, lw=0, rstride=1,
cstride=1,cmap=cm.gist_rainbow_r)
plt.axis('off')
plt.show()
效果如下

其公式为
p = π 2 exp ( − t 8 π ) u = 1 − 1 2 ( 1 − mod ( 3.6 t , 2 π ) π ) 4 y = 2 ( x 2 − x ) 2 sin p r = u ( x sin p + y cos p ) X = r cos t Y = r sin t Z = u ( x cos p − y sin p ) \begin{aligned} p &= \frac{\pi}{2}\exp(-\frac{t}{8\pi})\\ u &= 1-\frac{1}{2}(1-\frac{\operatorname{mod}(3.6t, 2\pi)}{\pi})^4\\ y &= 2(x^2-x)^2\sin p\\ r &= u(x\sin p+y\cos p)\\ X &= r\cos t\\ Y &= r\sin t\\ Z &= u(x\cos p-y\sin p) \end{aligned} puyrXYZ=2πexp(−8πt)=1−21(1−πmod(3.6t,2π))4=2(x2−x)2sinp=u(xsinp+ycosp)=rcost=rsint=u(xcosp−ysinp)
旋转的玫瑰
但是,如果只有这一朵花,就算色彩很绚丽,看久了也会感觉枯燥,所以下面来给这张图片加上一点动作,比如让这朵花在空间中旋转,方法非常简单,只要乘上一个旋转矩阵就OK为了书写方便,记 S θ = sin θ , C θ = cos θ S_\theta=\sin\theta, C_\theta=\cos\theta Sθ=sinθ,Cθ=cosθ,可列出下表。
| R x ( θ ) R_x(\theta) Rx(θ) | R x ( θ ) R_x(\theta) Rx(θ) | R x ( θ ) R_x(\theta) Rx(θ) |
|---|---|---|
| [ 1 0 0 0 C θ − S θ 0 S θ C θ ] \begin{bmatrix}1&0&0\\0&C_\theta&-S_\theta\\0&S_\theta&C_\theta\\\end{bmatrix} 1000CθSθ0−SθCθ | [ C θ 0 S θ 0 1 0 − S θ 0 C θ ] \begin{bmatrix}C_\theta&0 &S_\theta\\0&1&0\\-S_\theta&0&C_\theta\\\end{bmatrix} Cθ0−Sθ010Sθ0Cθ | [ C θ S θ 0 − S θ C θ 0 0 0 1 ] \begin{bmatrix}C_\theta &S_\theta&0\\-S_\theta&C_\theta&0\\0&0&1\end{bmatrix} Cθ−Sθ0SθCθ0001 |
下面的代码的含义就是,玫瑰花绕着Z轴旋转。
from matplotlib import animation
import imageio
cos = lambda th : np.cos(np.deg2rad(th))
sin = lambda th : np.sin(np.deg2rad(th))
# 此为旋转矩阵
Rz = lambda th : np.array([
[cos(th) , -sin(th), 0],
[sin(th), cos(th), 0],
[0 , 0, 1]])
xyz = np.array([X,Y,Z]).reshape(3,-1)
gifImgs = []
for n in np.arange(0,30,1):
xd,yd,zd = (Rx(n)@Ry(n)@Rz(n)@xyz).reshape(3,1151,25)
ax = plt.subplot(projection='3d')
ax.plot_surface(xd,yd,zd, lw=0, rstride=1,
cstride=1,cmap=cm.gist_rainbow_r)
plt.axis('off')
plt.savefig("%d.jpg" % n)
gifImgs.append(imageio.imread("%d.jpg" % n))
imageio.mimsave("test.gif",gifImgs,fps=5)
ani = animation.FuncAnimation(fig, animate,
range(0, 360, 2), interval=25, blit=True)
#plt.show()
ani.save("zyx.gif")
但最后的效果不太理想,貌似在抽搐,感觉非常离奇
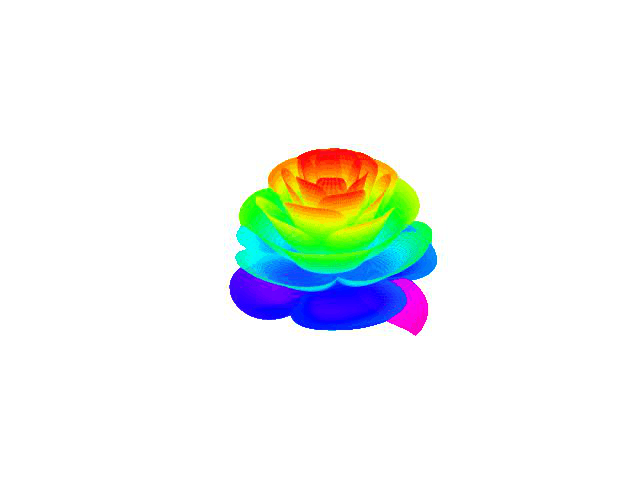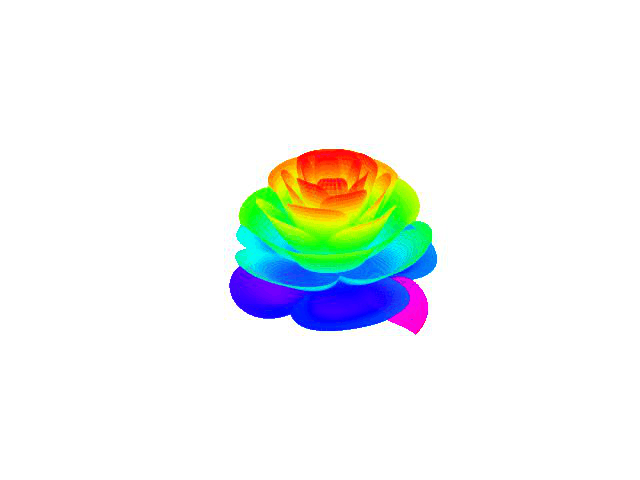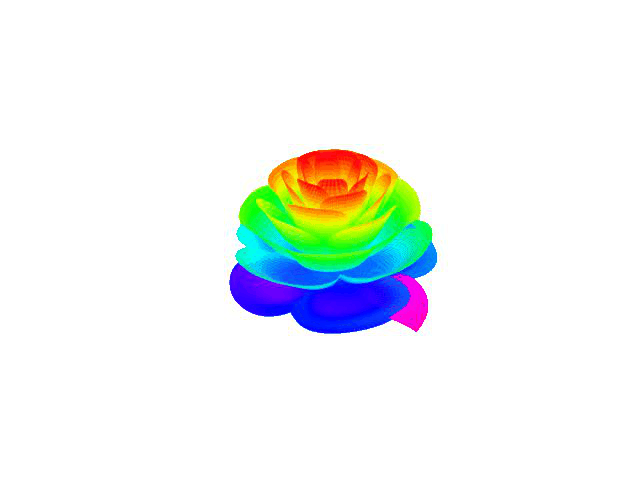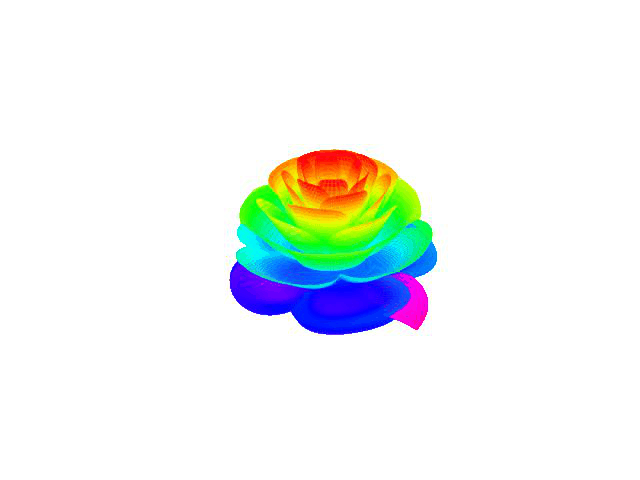

![[CTF/网络安全] 攻防世界 backup 解题详析](https://img-blog.csdnimg.cn/e3f68fb1108e463eb5897599da54893e.png#pic_center)