0.前言
字符串函数
strstr相信大家都不陌生–就是在一个字符串(主串)中找查找另一个字符串(子串),并返回子串在主串中的位置。那么这个函数是怎么实现的呢?这就涉及字符串匹配的问题,本章就让我们一起学习有关串匹配的两个算法–BF算法和KMP算法🐇🐇🐇
1.BF算法
BF算法,即暴力(Brute Force)算法,是普通的模式匹配算法,BF算法的思想就是将目标串S的第一个字符与模式串T的第一个字符进行匹配,若相等,则继续比较S的第二个字符和 T的第二个字符;若不相等,则比较S的第二个字符和T的第一个字符,依次比较下去,直到得出最后的匹配结果。BF算法是一种蛮力算法。这是百度百科对BF算法的简介。
图形理解:
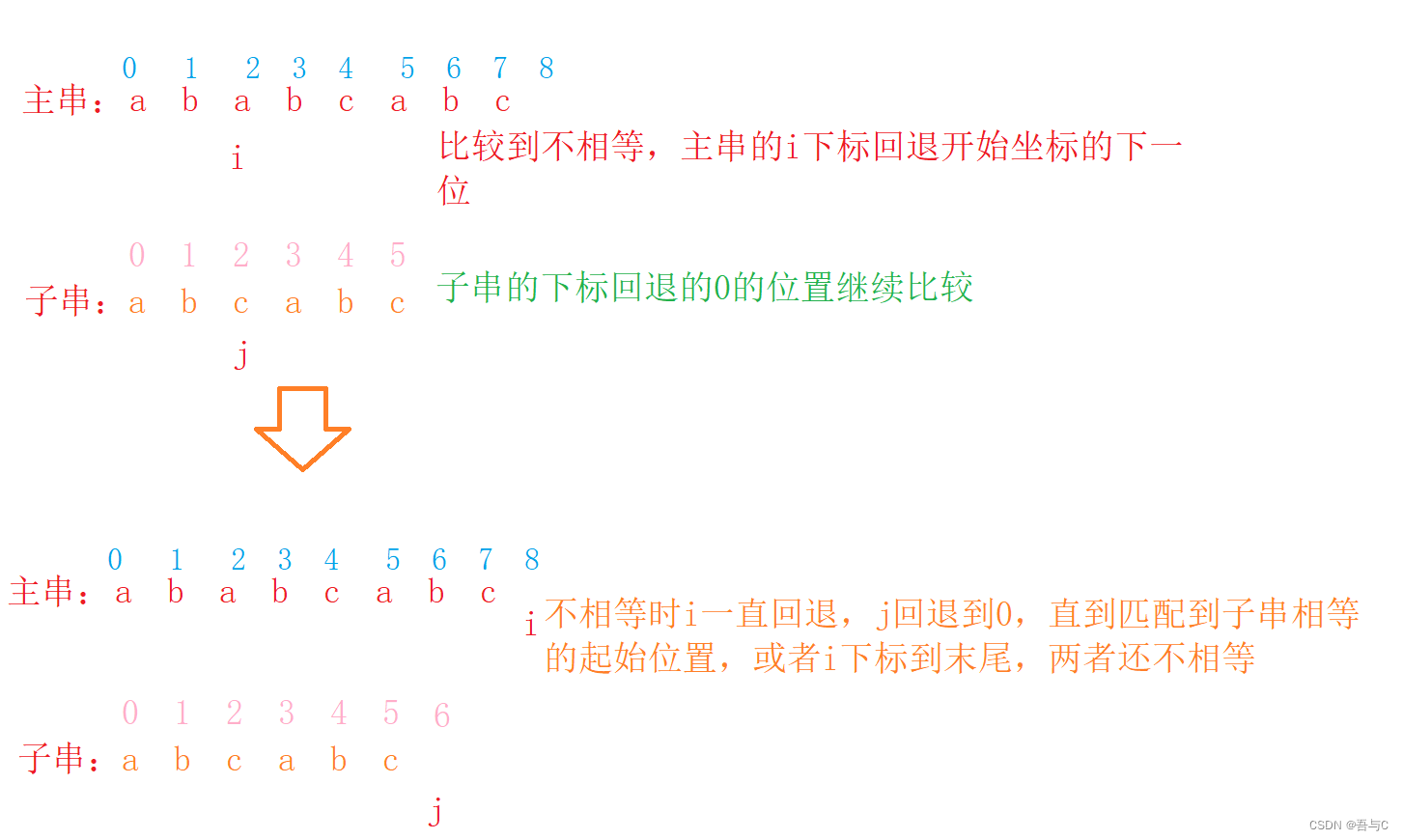
我们假设主串用i下标进行访问,子串用j下标进行访问,刚开始主串i和子串下标j都是从0开始进行两个字符串的匹配。如果匹配到不相等,i下标回到刚刚位置的下一个位置,j下标回到0的位置,直到主串i下标到末尾为止(匹配失败),或子串下标j到达末尾(匹配成功)。
代码实现
#define _CRT_SECURE_NO_WARNINGS 1
#include<stdio.h>
#include<string.h>
#include<assert.h>
//串的匹配算法--BF算法
int BF(const char* str, const char* sub)
{
if (str == NULL || sub == NULL)
{
return -1;
}
int lenstr = strlen(str);
int lensub = strlen(sub);
if (lenstr == 0 || lensub == 0)
{
return -1;
}
int i = 0;//记录主串的位置
int j = 0;//记录子串的位置
while (i < lenstr && j < lensub)
{
if (str[i] == sub[j])
{
i++;
j++;
}
else
{
//i和j是同时走的
i = i - j + 1;//i回到刚才比较的位置的下一个位置
j = 0;//子串回到起始位置
}
}
while (j >= lensub)
{
//返回子串在主串的起始位置
return i - j;
}
return -1;
}
int main()
{
char arr1[] = "ababcabc";
char arr2[] = "abcabc";
printf("%d", BF(arr1, arr2));
return 0;
}
代码运行的结果如下:
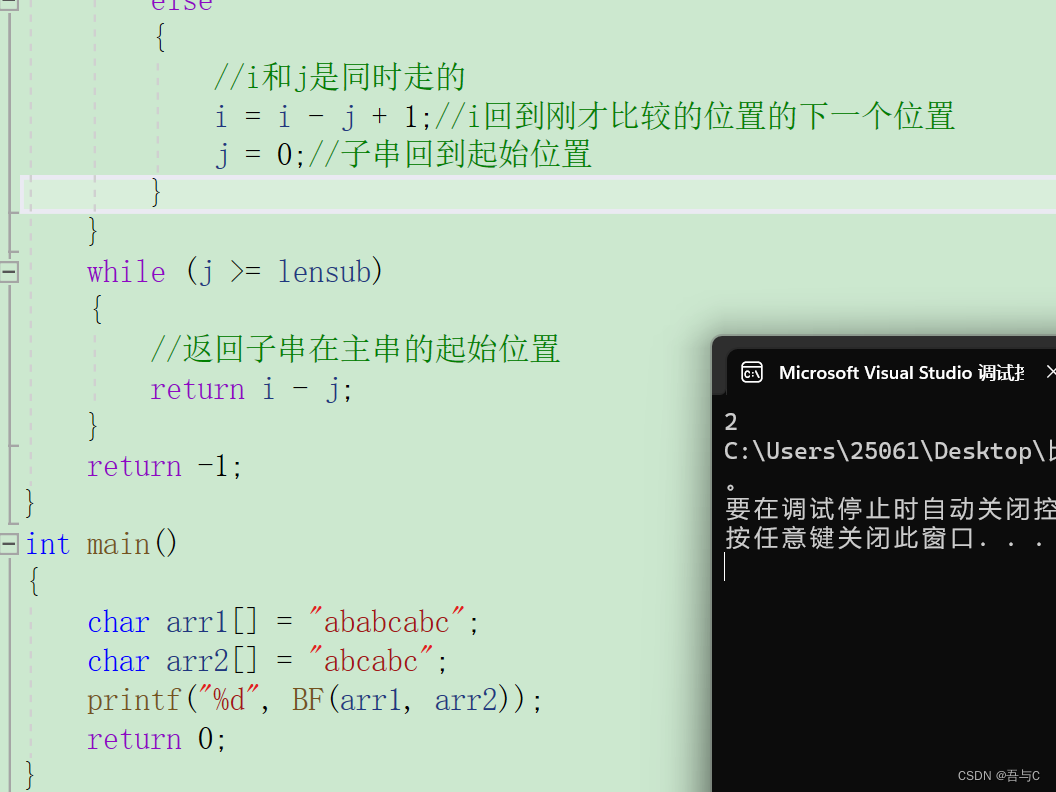
小结: 假设主串长度为M,子串长度为N,所以BF算法的时间复杂度:O(M*N),用BF算法进行字符串的匹配非常“暴力”。😾😾😾
2.KMP算法
KMP算法是一种改进的字符串匹配算法,由D.E.Knuth,J.H.Morris和V.R.Pratt提出的,因此人们称它为克努特—莫里斯—普拉特操作(简称KMP算法)。KMP算法的核心是利用匹配失败后的信息,尽量减少模式串与主串的匹配次数以达到快速匹配的目的。具体实现就是通过一个next()函数实现,函数本身包含了模式串的局部匹配信息。这是百度百科对KMP算法的简介。
最长相等前后缀
在认识KMP算法之前,首先我们需要认识什么是相等前后缀,🦀🦀🦀前缀:从字符串第一个字符开始,不包括最后一个字符的字符串部分;后缀:包含最后一个字符,不包括第一个字符的字符串部分
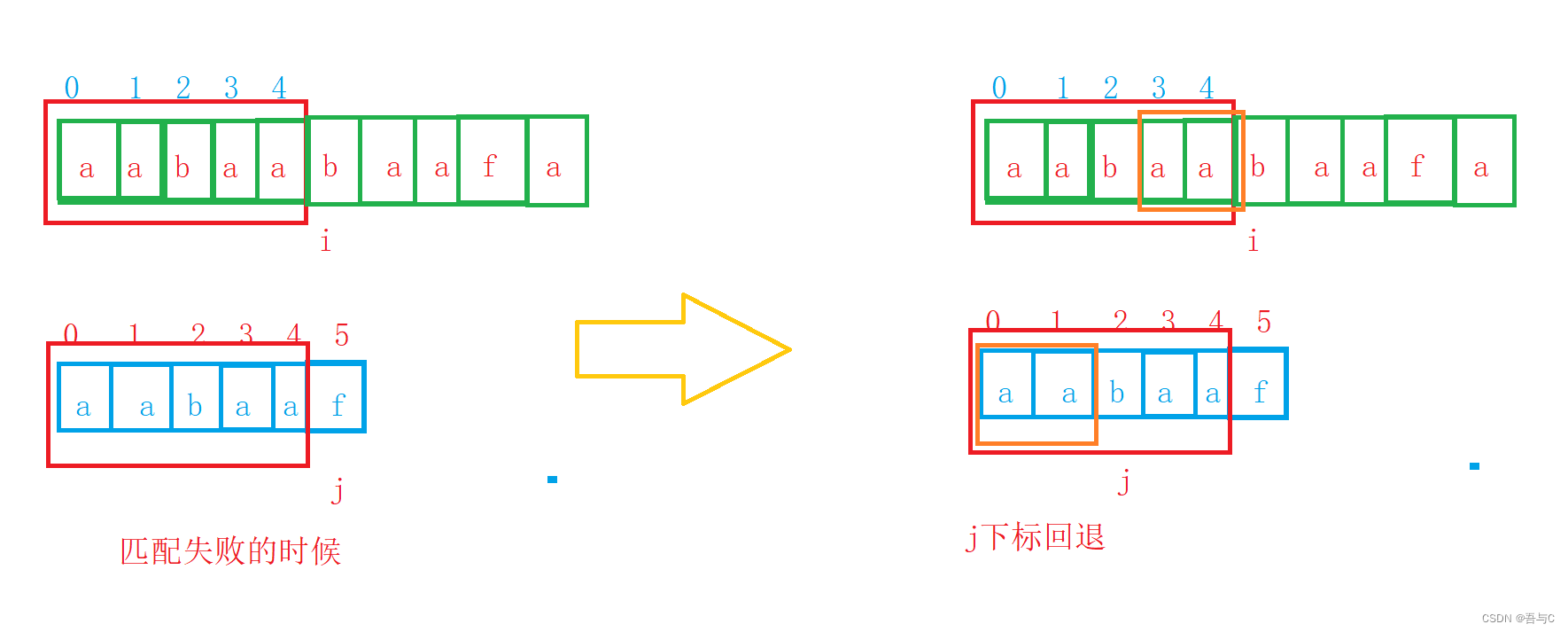
然后我们得知道主串和子串在匹配失败的时候,主串和子串不相等字符的前面的字符串是一样的,这时只需要找到该字符串的最长相等前后缀长度,主串i不用回退,子串下标j回到的位置(即前缀字符的下一个位置)(即刚好为最长相等前后缀的长度)。
通过观察可以发现,只需要从在主串中相同部分字符串后缀的下一个位置,在子串中相同部分字符串前缀的下一个位置开始匹配即可。
next数组
要达到上面主串和子串匹配主串下标i不用回退的,子串下标j回到特定位置的效果,需要在主串和子串匹配不相等时,让最长相等前后缀的长度作为子串下标j回退的位置,这时我们可以用数组进行记录,并把这个数组取名为next(意义是j的下一个位置)。那么我们该怎么实现next数组呢?🐰🐨🐻
KMP算法的精髓就是next[j]=k,不同的j值要用一个K来实现,其中K就是子串下标j回退的位置。
而 K 的值是这样求的:
1、规则:找到匹配成功部分的两个相等的真子串(不包含本身),一个以下标 0 字符开始,另一个以 j-1 下标;
字符结尾。
2、不管什么数据 next[0] = -1;next[1] = 0;在这里,我们以下标来开始,而说到的第几个第几个是从 1 开始;
匹配相等的情况

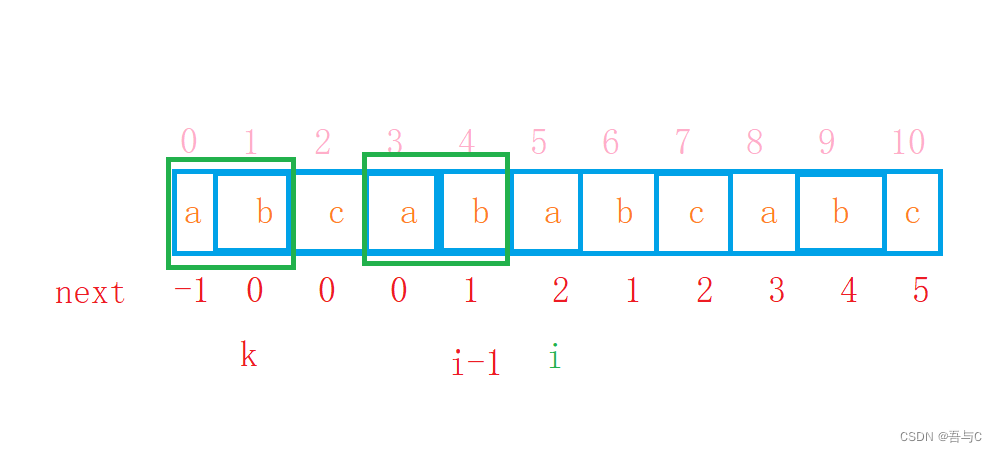
因为已经知道next数组前面两位,我们知道求第i位则就需要判断
sub[i - 1] == sub[k],如果相等,next[i]=k+1
匹配不相等的情况
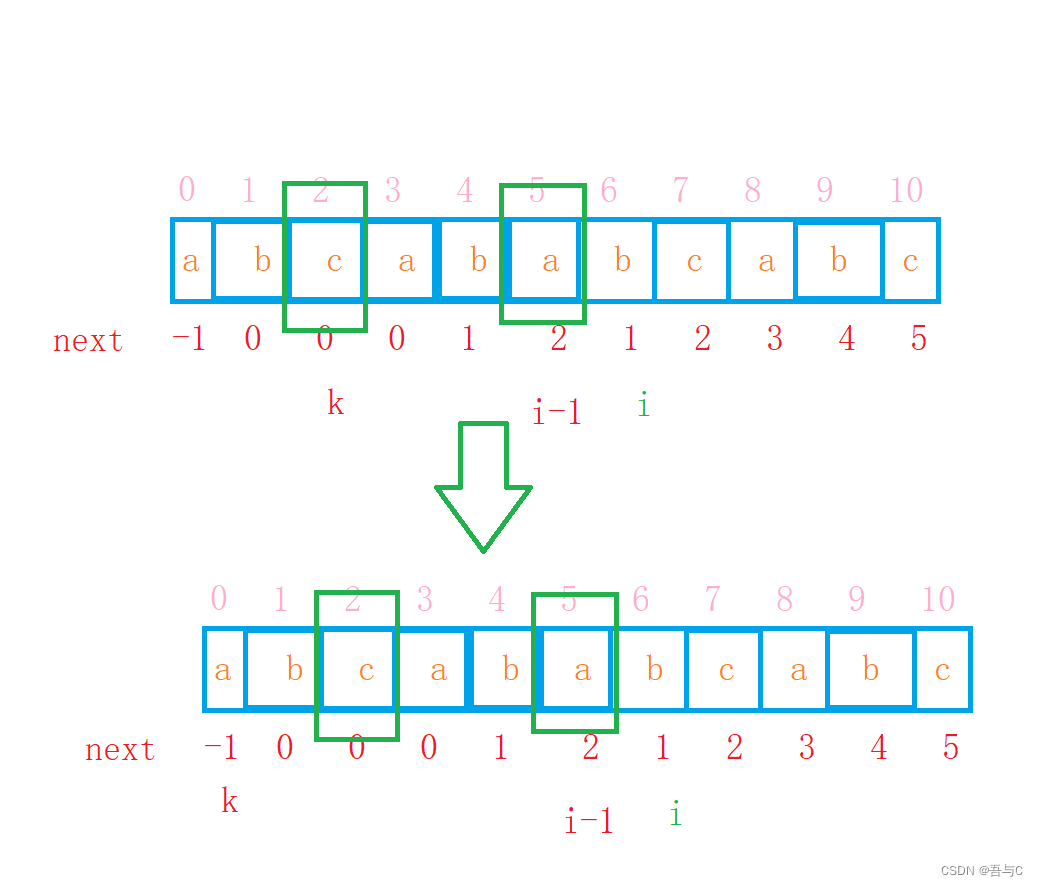
如果遇到不相等的情况,k回退到next[k]的位置继续,再比较继续比较是否相等,直到匹配到
sub[i - 1] == sub[k]相等或者k=-1为止
next数组代码实现:
void Getnext(const char* sub, int* next, int lensub)
{
//默认next前两个数分别为-1,0
next[0] = -1;
next[1] = 0;
int i = 2;//当前下标的位置
int k = 0;//前一项的存放的值(回溯的位置)
while (i < lensub)
{
//子串前缀末尾和后缀末尾字符相等
if (k==-1||sub[i - 1] == sub[k])
{
next[i] = k + 1;
k++;
i++;
}
else
{
k = next[k];
}
}
}
KMP代码实现
#include<stdio.h>
#include<string.h>
#include<assert.h>
void Getnext(const char* sub, int* next, int lensub)
{
//默认next前两个数分别为-1,0
next[0] = -1;
next[1] = 0;
int i = 2;//当前下标的位置
int k = 0;//前一项的存放的值(回溯的位置)
while (i < lensub)
{
//子串前缀末尾和后缀末尾字符相等
if (k==-1||sub[i - 1] == sub[k])
{
next[i] = k + 1;
k++;
i++;
}
else
{
k = next[k];
}
}
}
int KMP(const char* str, const char* sub)
{
if (str == NULL || sub == NULL)
{
return -1;
}
int lenstr = strlen(str);
int lensub = strlen(sub);
if (lenstr == 0 || lensub == 0)
{
return -1;
}
int* next = (int*)malloc(sizeof(int) * lensub);
Getnext(sub, next, lensub);
int i = 0;//记录主串的位置
int j = 0;//记录子串的位置
//假设主串和子串在第i个位置不相等
//那么主串的前i-1个和子串的前i-1个
//在子串最长相等的前缀和后缀
//这时只需要在主串的后缀、子串的前缀开始匹配
//所以主串位置的i不用回退
//若是前i-1的子串最长相等的前缀和后缀的长度为0
//那么子串j回到0位置,同时说明从主串前i-1个位置开始匹配
//都不会和子串匹配,直接从i位置开始匹配
while (i < lenstr && j < lensub)
{
if (j==-1||str[i] == sub[j])
{
i++;
j++;
}
else
{
j = next[j];
}
}
if (j >= lensub)
{
return i - j;
}
return -1;
}
int main()
{
char arr1[] = "aabaabaafa";
char arr2[] = "aabaaf";
printf("%d", KMP(arr1, arr2));
return 0;
}
小结: 假设主串长度为M,子串长度为N,KMP算法的时间复杂度为O(M+N),大大提高字符串匹配的效率,是一个很“友好”的算法。🎉🎉🎉
总结
本章我们一起学习字符串匹配算法–BF算法和KMP算法的实现,希望对大家解决字符串匹配问题有些许帮助!感谢大家阅读,如有不对,欢迎纠正!!!🎠🎠🎠