composition(组成)
k-composition:
20块巧克力分给4个小朋友,有几种分法?
隔板法,19个间隙插入3个板,
推广:n块分给k个
weak k-composition:
20块巧克力分给4个小朋友,每个小朋友至少有一块,有几种分法?
先给4个小朋友每人一块,再用隔板法,
推广:n块分给k个,每个人至少有一个
Set partition(集合划分)

将一个集合划分成含有集合元素的非空集合,并保证所有划分成的子集并集为原集合

把含有n个元素的集合划分成k份的方案数定义为斯特林第二类数,记为S(n,k)

左边:将n个元素划分成k份的方案数S(n,k);
右边:最大元素n若划分时单独成为一个集合,则剩下K-1个集合需要在n-1个数中划分好,若划分时不时单独的集合,则n-1个数划分成k分,最大的数选择其中一份加入其中,选择种数为k种,故右边为S(n-1,k-1)+k*S(n-1,k)
Corolary
The number of all surjective functions 𝑓:[𝑛] → [𝑘] is 𝑘! ⋅ 𝑆 (𝑛, 𝑘) .
符号说明:[n]为1~n的数的集合

Bell number
 Integer partition(整数划分)
Integer partition(整数划分)

注意:1+4和4+1视为同一种

一些定义:p(n)是n的整数划分方案数,
是n的集合划分方案数
Ferrers diagram(菲勒斯图)

上层的格子数不少于下层的格子数
如果我们沿着菲勒斯图的对角线翻转,那么就得到了它的共轭图

可以利用菲勒斯图解释一些公式
1.整数n拆分成最大数为k的拆分数,和数n拆分成k个数的和的拆分数相等
因整数n拆分成k个数的和的拆分可用一k行的图像表示。所得的Ferrers图像的共轭图像最上面一行有k个格子(Flip翻转)
2.将集合划分成奇数份的方案数等于所有总数为n的自共轭图的种数
这个也很好解释,因为自共轭沿着y = -x对称,组成自共轭图的点数一定是奇数个的
整数划分和集合划分之间的关系


为n的整数划分方案数,而
为n的集合划分方案数,显然这两者不等同,因为整数划分时不同元素排序视为同一种方案,例如{1,2,3},{4,5}和{1,2,4},{3,5}是一样的,都视为5 = 3 + 2。
因此,我们需要依次除以每个被划分成的数的阶乘,如划分成了(3,2,1),3个数全排列为3!视为一种方案,除以3!,同理,再除以2!和1!
递推关系


Derangement(错排)
错排问题分析及递推在第一讲中已经写过,这里就跳过了
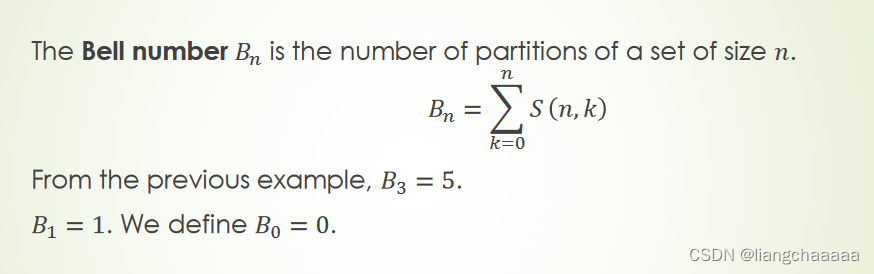
![[创业之路-69]:对管理理念的理解和解读](https://img-blog.csdnimg.cn/img_convert/804116112f6dc8f5e09b1f850127b937.jpeg)