Dijkstra单源最短路径

什么是单源最短路径

描述：给定一个带权有向图G = (V，E)，其中每条边的权时非负数。另外，给定V中的一个顶点，称为源。现在要计算从源到所有其他各顶点的最短路长度。这里路的长度是指路上各边权之和。这个问题通常称为单源最短路径问题。

以下图的题为例，进行分析。

设源点为顶点1，采用Dijkstra算法求下图中源V0为到其余各顶点的最短路径。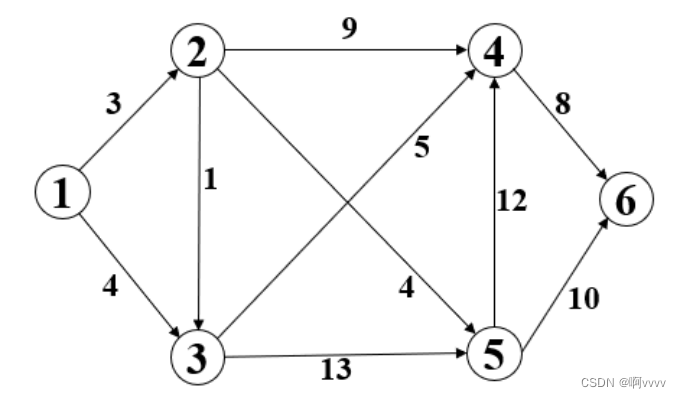

采用Dijkstra算法（本质是贪心算法）

该算法的基本思想是，设置顶点集合S，并且不断地做贪心选择来扩充这个集合。初始时，S中仅含有源点。设U是G的某一个顶点，把源到U且中间只经过S中顶点的路称为从源到u的特殊路径，并用dist记录当前每个顶点所对应的最短特殊路径长度。Dijkstra算法每次从V-S中取出具有最短特殊路上度的顶点U，将U添加到S中，同时对数组dist做必要修改。一旦S包含了所有V中顶点，dist就记录了从源到其他所有顶点的最短路径长度。

所以究竟是怎么个贪心策略？我们把所有过程走一遍

对于源点v1，我们初始化。dist [ i ]源点到i的距离。vis [ i ]当前点i是否已经加入S集合。pre [ i ] 当前点 i 的前一个节点

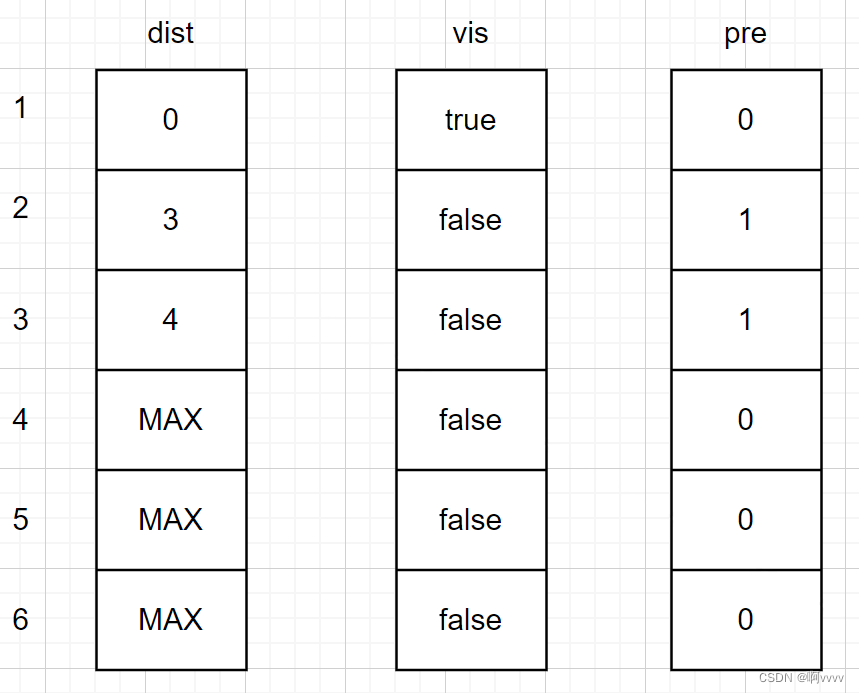
对于下一个点的选择，我们选择距离最短的那个点继续，即v2。

对于v2点，存在三条边：v2 — > v3，v2 — > v4，v2 — > v5。将dist数组进行更新，如果当前点有其它点遍历到了，那么选择最小的距离。

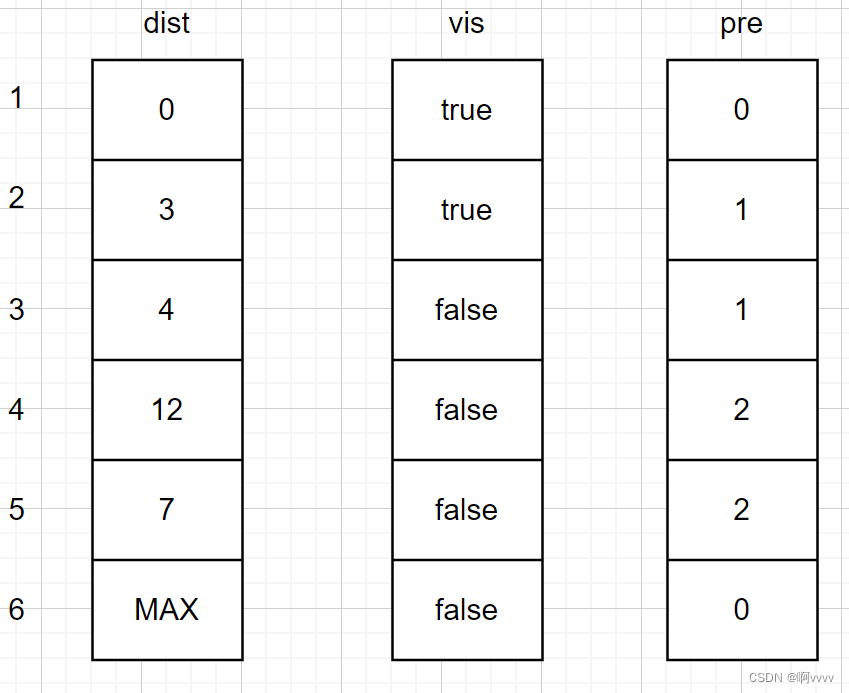
对于下一个点，依旧选择最短的，此时选择从v3出发。此时会有点冲突，v2已经到达了v4了，此时v3也到达了v4，这个时候就要更新dist[4]的值

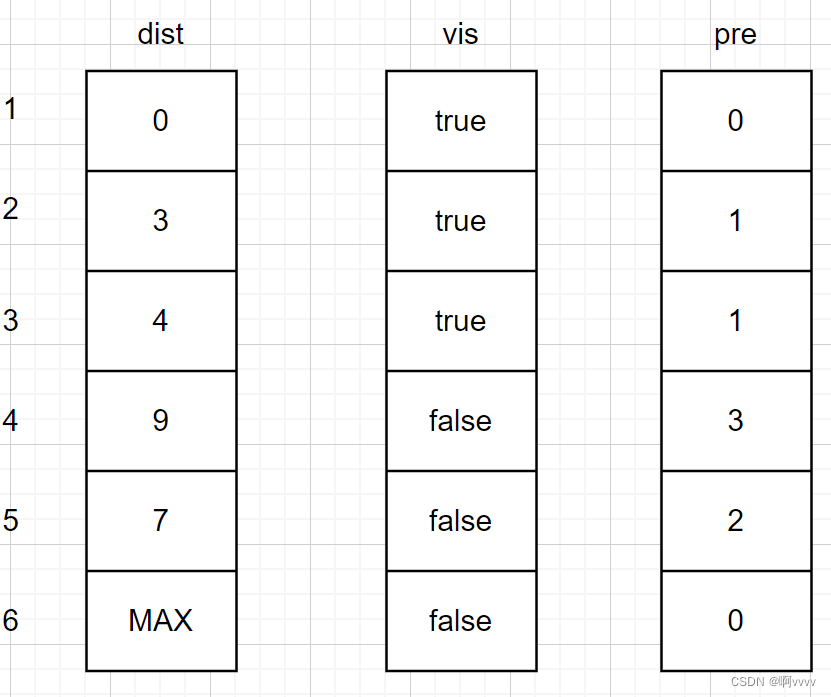
对于下一个点，依旧选择最短的且没有被加入集合S的，v5。

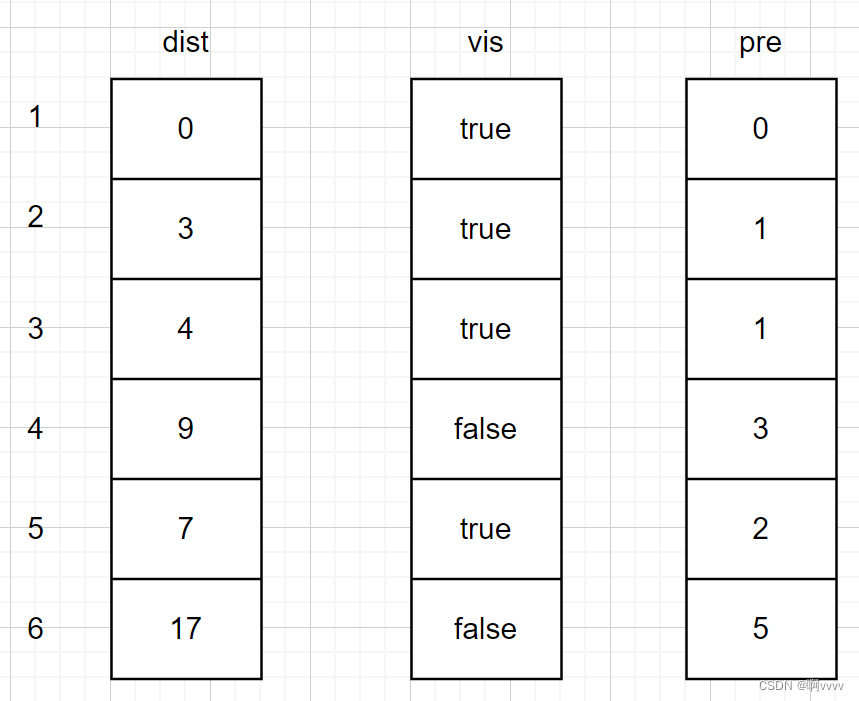
对于下一个点，依旧选择最短的且没有被加入集合S的，v4。

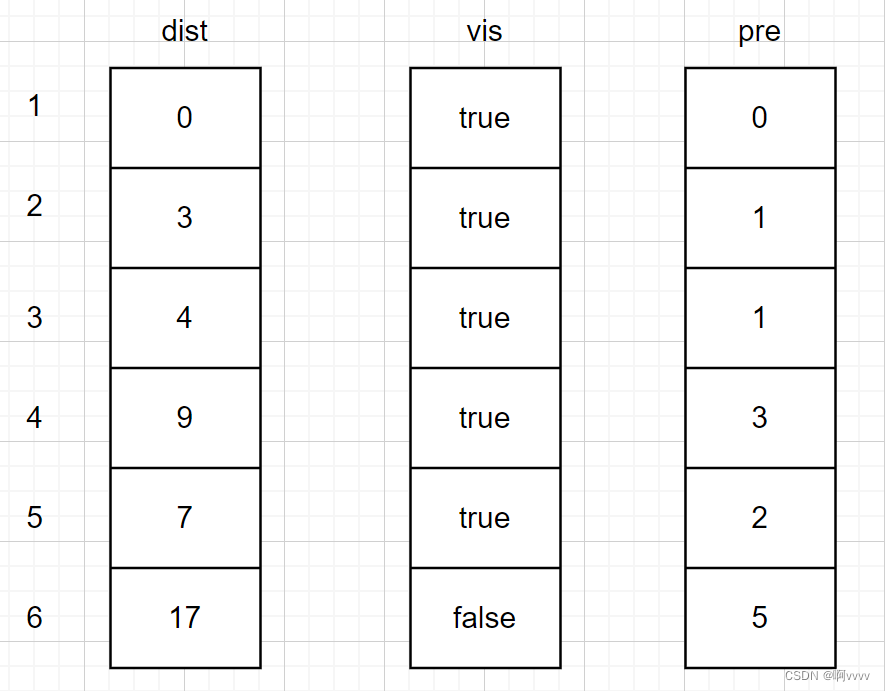
对于下一个点，依旧选择最短的且没有被加入集合S的，v6。

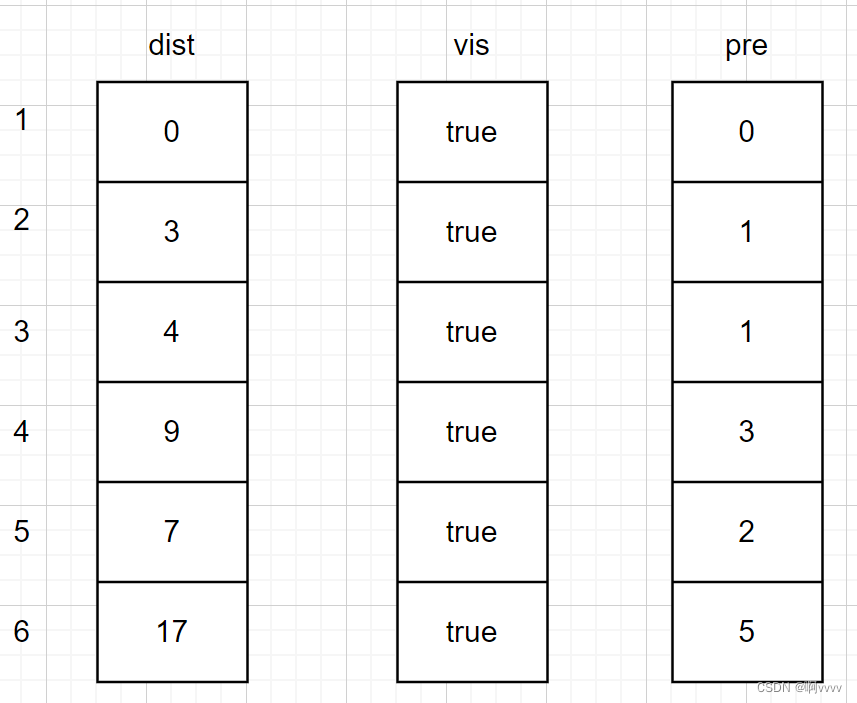
具体Java代码实现

public class TestDijkstra {
    public static void main(String[] args) {
        int[] dist = new int [7]; //原点到各点的距离
        int[] prev = new int[7]; //前一个节点
        int[][] g = new int[7][7]; //邻接矩阵
        for (int i = 0; i < 7; i++) {
            Arrays.fill(g[i],Integer.MAX_VALUE);
        }
        //添加边权
        g[1][2] = 3;
        g[1][3] = 4;
        g[2][3] = 1;
        g[2][4] = 9;
        g[2][5] = 4;
        g[3][4] = 5;
        g[3][5] = 13;
        g[4][6] = 8;
        g[5][4] = 12;
        g[5][6] = 10;
        dijkstra(1,prev,dist,g);
    }
    public static void dijkstra(int v ,int []prev,int [] dist, int [][] g){
        int n = dist.length - 1;
        if(v < 1 || v > n){
            return;
        }
        //当前节点是否被加入到集合
        boolean[] vis = new boolean[n+1];
        //初始化，第一个到自己，最短路为0，其余点都为无穷
        for (int i = 1; i <= n ; i++) {
            dist[i] = g[v][i];
            vis[i] = false;
            if(dist[i] == Integer.MAX_VALUE){
                prev[i] = 0;
            }else {
                prev[i] = v;
            }
        }
        dist[v] = 0;
        vis[v] = true;
        for (int i = 1; i < n; i++) {
            int tmp = Integer.MAX_VALUE;
            int u = v;
            //选则一个可达最短距离点作为下一次的起点
            for(int j = 1; j <= n; j++){
                if( !vis[j]  && (dist[j] < tmp) ){
                    u = j;
                    tmp = dist[j];
                }
            }
            //最短点加入集合
            vis[u] = true;
            
            //更新dist数组，没有点到则写自己的距离，有点到就写自己与已到点距离的最小值
            for(int j = 1; j <= n;j++){
                if(( !vis[j] ) && ( g[u][j] < Integer.MAX_VALUE )){
                    int newDist = dist[u] + g[u][j];
                    if( newDist < dist[j] ){
                        dist[j] = newDist;
                        prev[j] = u;
                    }
                }
            }
            System.out.println(Arrays.toString(dist));
            System.out.println(Arrays.toString(vis));
            System.out.println(Arrays.toString(prev));
        }
    }
}