( 动态规划) 115. 不同的子序列 ——【Leetcode每日一题】

news2024/9/21 10:37:40

❓115. 不同的子序列

难度：困难

给你两个字符串 s 和 t ，统计并返回在 s 的 子序列 中 t 出现的个数。

题目数据保证答案符合 32 位带符号整数范围。

示例 1：

输入：s = “rabbbit”, t = “rabbit”
输出：3
解释：
如下所示, 有 3 种可以从 s 中得到 “rabbit” 的方案。
ra b bbit
rab b bit
rabb b it

示例 2：

输入：s = “babgbag”, t = “bag”
输出：5
解释：
如下所示, 有 5 种可以从 s 中得到 “bag” 的方案。
ba b g bag
ba bgba g
b abgb ag
ba b gb ag
babg bag

提示：

1 <= s.length, t.length <= 1000
s 和 t 由英文字母组成

💡思路：动态规划

本题可以使用动态规划，可以将本题拆分，拆分成若干个子问题，只考虑其中一步；

如比较字符串 s 的第 i 个字符和字符串 t 的第 j 个字符

如果 s[i] 等于 t[j] ， s 的第 i 个字符可取可不取，总个数为两者之和：
1. 若取，s的前i个字符串 的 子序列 中 t的前j个字符串出现的个数等于 s的前i - 1个字符串 的 子序列 中 t的前j - 1个字符串出现的个数；
2. 若不取，s的前i个字符串 的 子序列 中 t的前j个字符串出现的个数等于 s的前i - 1个字符串 的 子序列 中 t的前j个字符串出现的个数；
如果 s[i] 不等于 t[j] ，则 s的前i个字符串 的 子序列 中 t的前j个字符串出现的个数等于 s的前i - 1个字符串 的 子序列 中 t的前j个字符串出现的个数；

定义一个二维 dp 数组，dp[i][j] ，表示s的前i个字符串 的 子序列 中 t的前j个字符串出现的个数。状态转移公式为：

若s[i] == t[j]，则：
$d p [i] [j] = d p [i - 1] [j - 1] + d p [i - 1] [j]$
若s[i] != t[j]，则：
$d p [i] [j] = d p [i - 1] [j]$

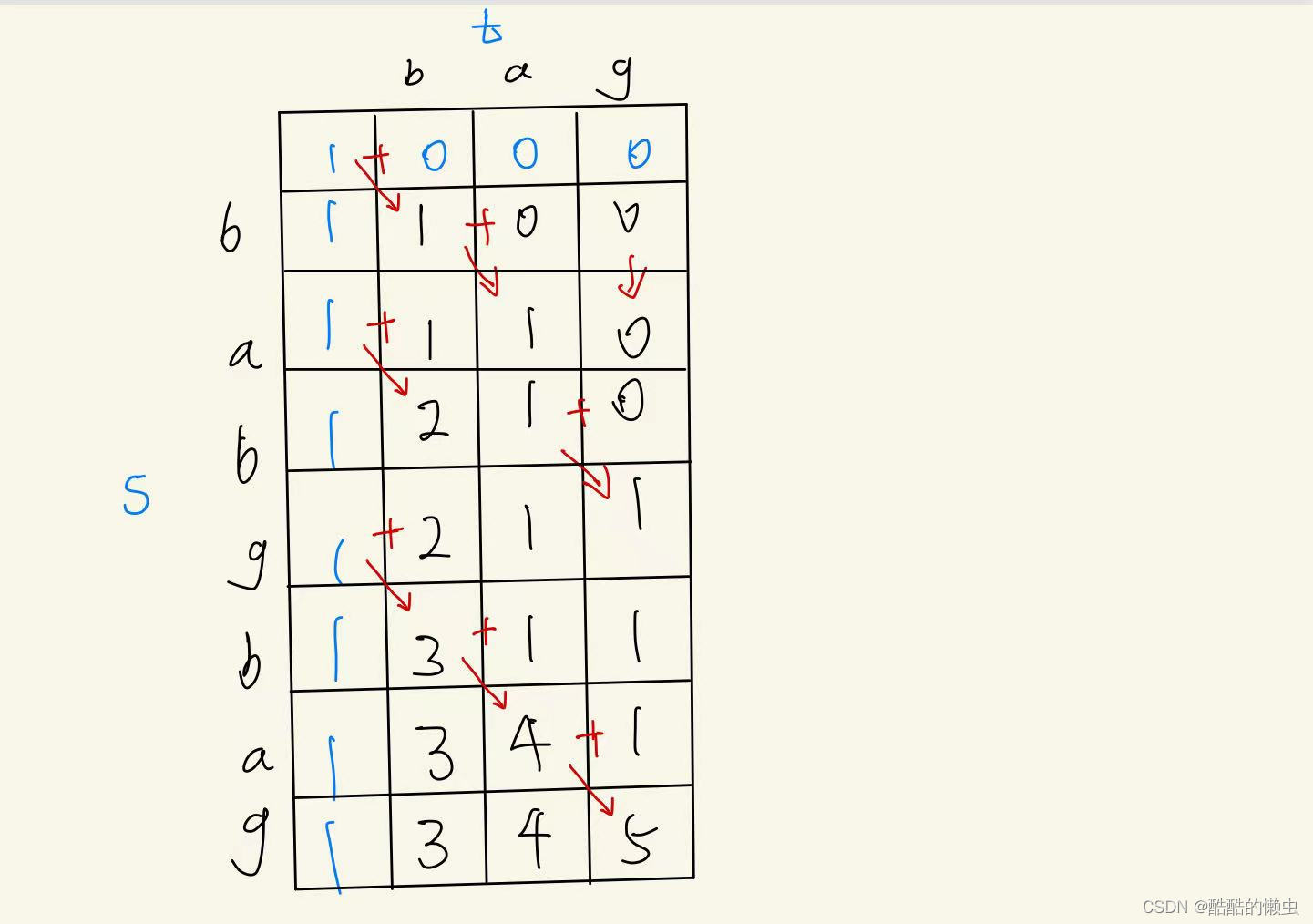
示例2的dp 数组如下：

在这里插入图片描述

⭐️ 空间优化：

由上述状态转移公式可知，dp[i][j] 只与上一行有关，即只需要一维dp数组即可，但是要逆序遍历，此时的状态转移公式:

若s[i] == t[j]，则：
$d p [j] = d p [j - 1] + d p [j]$
若s[i] != t[j]，则：
$d p [j] = d p [j]$

注意：若s 的长度小于t的长度，则一定不存在，返回 0 ；若长度相等，但字符串不等，则也是返回 0。

🍁代码：(Java、C++)

Java

class Solution {
    public int numDistinct(String s, String t) {
        int m = s.length();
        int n = t.length();
        if(m < n || (m == n && !s.equals(t))) return 0;
        int[][] dp= new int[m + 1][n + 1];
        for(int i = 0; i <= m; i++) dp[i][0] = 1;
        for(int i = 1; i <= m; i++){
            for(int j = 1; j <= n; j++){
                if(s.charAt(i - 1) == t.charAt(j - 1)){
                    dp[i][j] = dp[i - 1][j - 1] + dp[i - 1][j];
                }
                else{
                    dp[i][j] = dp[i - 1][j];
                }
            }
        }
        return dp[m][n];
    }
}

C++

class Solution {
public:
    int numDistinct(string s, string t) {
        int m = s.size();
        int n = t.size();
        if(m < n || (m == n && s != t)) return 0;
        vector<vector<unsigned int>> dp(m + 1, vector<unsigned int>(n + 1));
        for(int i = 0; i <= m; i++) dp[i][0] = 1;
        for(int i = 1; i <= m; i++){
            for(int j = 1; j <= n; j++){
                if(s[i - 1] == t[j - 1]){
                    dp[i][j] = dp[i - 1][j - 1] + dp[i - 1][j];
                }
                else{
                    dp[i][j] = dp[i - 1][j];
                }
            }
        }
        return dp[m][n];
    }
};

⭐️ 空间优化：
Java

class Solution {
    public int numDistinct(String s, String t) {
        int m = s.length();
        int n = t.length();
        if(m < n || (m == n && !s.equals(t))) return 0;
        int[] dp= new int[n + 1];
        dp[0] = 1;
        for(int i = 1; i <= m; i++){
            for(int j = n; j > 0; j--){
                if(s.charAt(i - 1) == t.charAt(j - 1)){
                    dp[j] += dp[j - 1];
                }
            }
        }
        return dp[n];
    }
}

C++

class Solution {
public:
    int numDistinct(string s, string t) {
        int m = s.size();
        int n = t.size();
        if(m < n || (m == n && s != t)) return 0;
        vector<unsigned int> dp(n + 1);
        dp[0] = 1;
        for(int i = 1; i <= m; i++){
            for(int j = n; j > 0; j--){
                if(s[i - 1] == t[j - 1]){
                    dp[j] += dp[j - 1];
                }
            }
        }
        return dp[n];
    }
};