- 本章要求
1. 掌握支路电流法、叠加原理和戴维宁定理等电路的基本分析方法;
2. 了解实际电源的两种模型及其等效变换;
3. 了解非线性电阻元件的伏安特性及静态电阻、动态电阻的概念,以及简单非线性电阻电路 的图解分析法。
目录
一、电阻串并联连接的等效变换
1、电阻的串联
2、电阻的并联
3、电桥电路
4、电阻星形联结与三角形联结的等换
二、电源两种模型的等效变换
三、支路电流法
四、结点电压法
五、叠加原理
六、等效电源定理
1、戴维南定理
2、诺顿定理
七、课后习题
1、等效变换问题
2、化简电路问题
3、功率问题
4、电流问题
4.1 涉及支路电流法的求支路电路
4.2 涉及结点电压法的求支路电流
4.3 涉及叠加原理的求支路电流
一、电阻串并联连接的等效变换
- 等效变换是干什么的?
化简电路,降低分析电路的难度
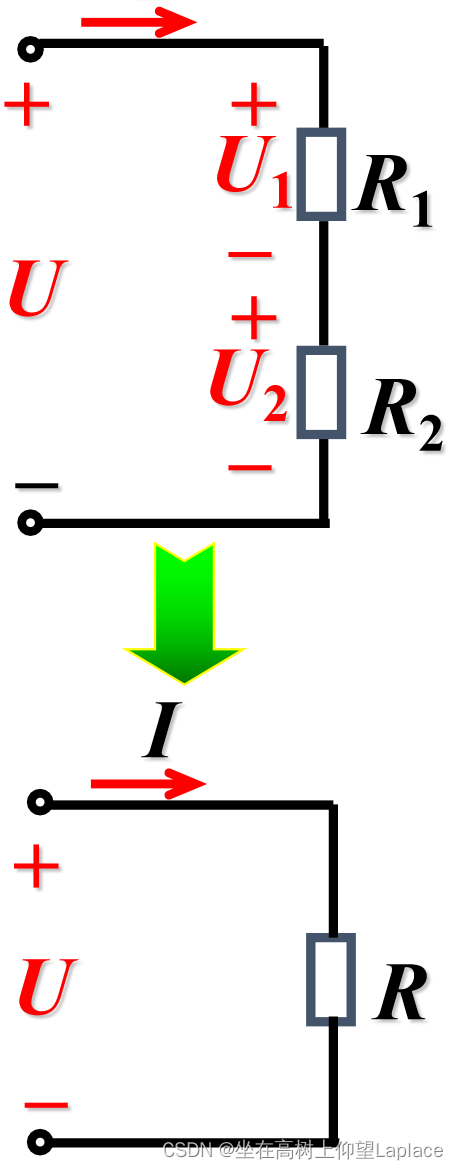
1、电阻的串联
特点
- 各电阻一个接一个地顺序相联
- 各电阻中通过同一电流
- 等效电阻等于各电阻之和:R =R1+R2
- 并联电阻上电流的分配与电阻成反比
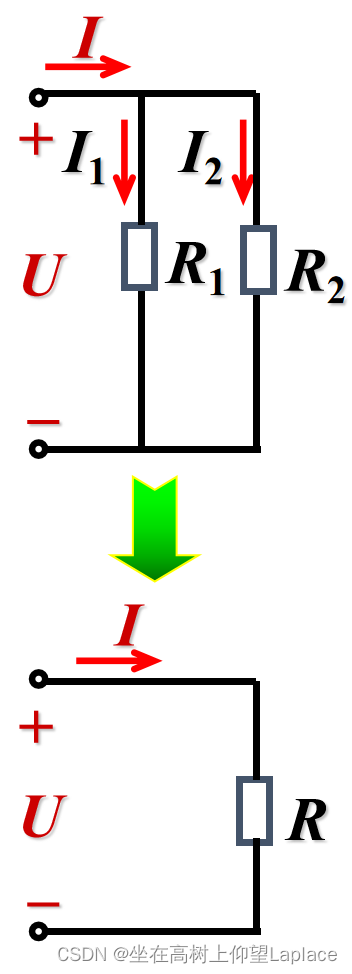
2、电阻的并联
特点
- 各电阻联接在两个公共的结点之间
- 各电阻两端的电压相同
- 等效电阻的倒数等于各电阻倒数之和:
- 并联电阻上电流的分配与电阻成反比
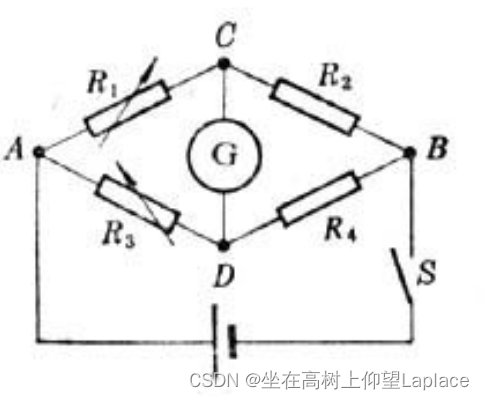
3、电桥电路
一般情况下R1、R3两端的电压不相等,即C、D两点间的电势不等,G中有电流通过。改变R1、R3的大小,可以使UAC=UAD,这时G中无电流通过。当G中无电流时叫做"电桥平衡"。本实验就是研究R1、R2、R3和R4之间满足什么关系时电桥平衡。(当R1XR4 = R2XR3,对角线支路中电流为零,电桥处于平衡状态)
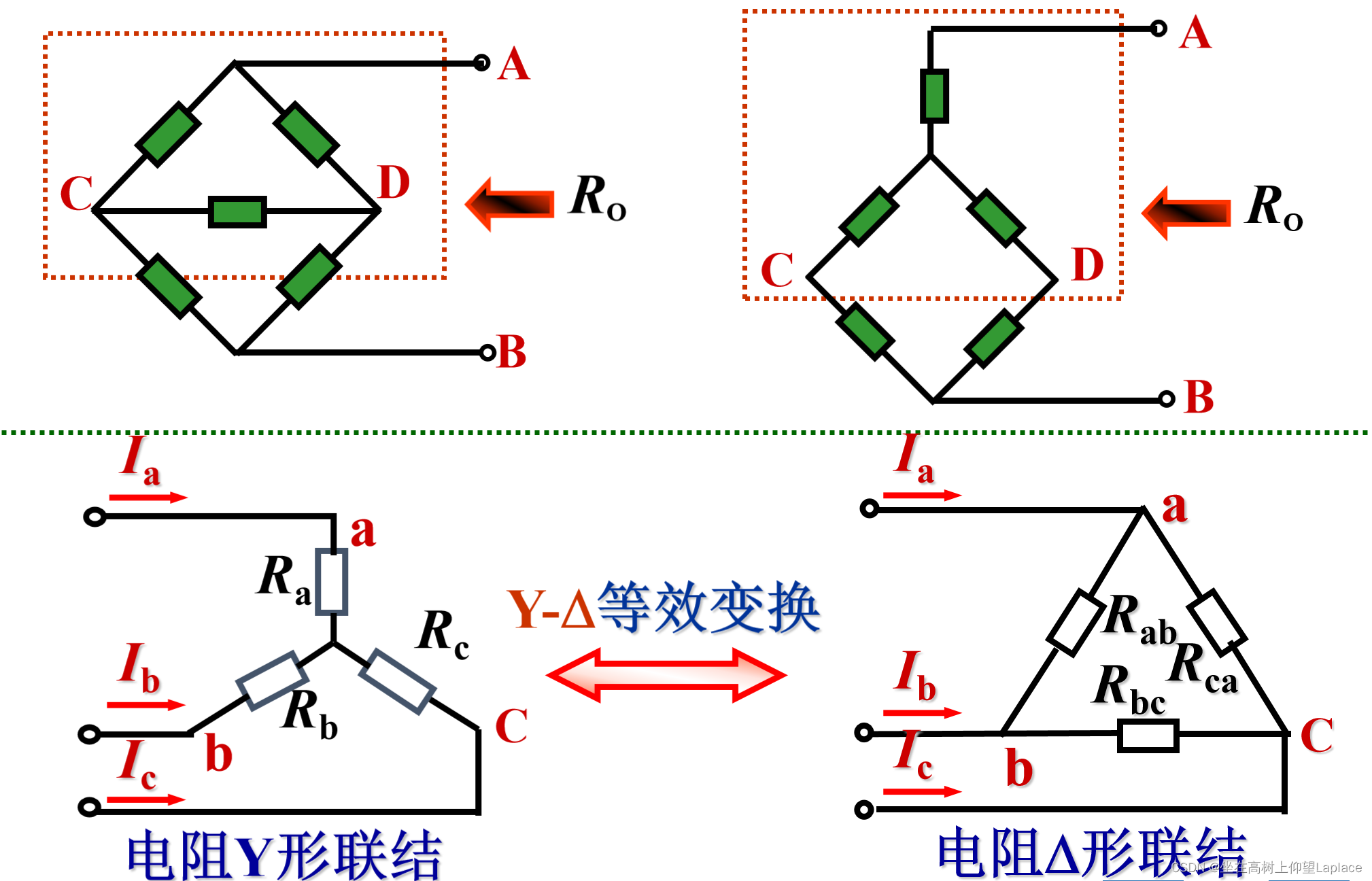
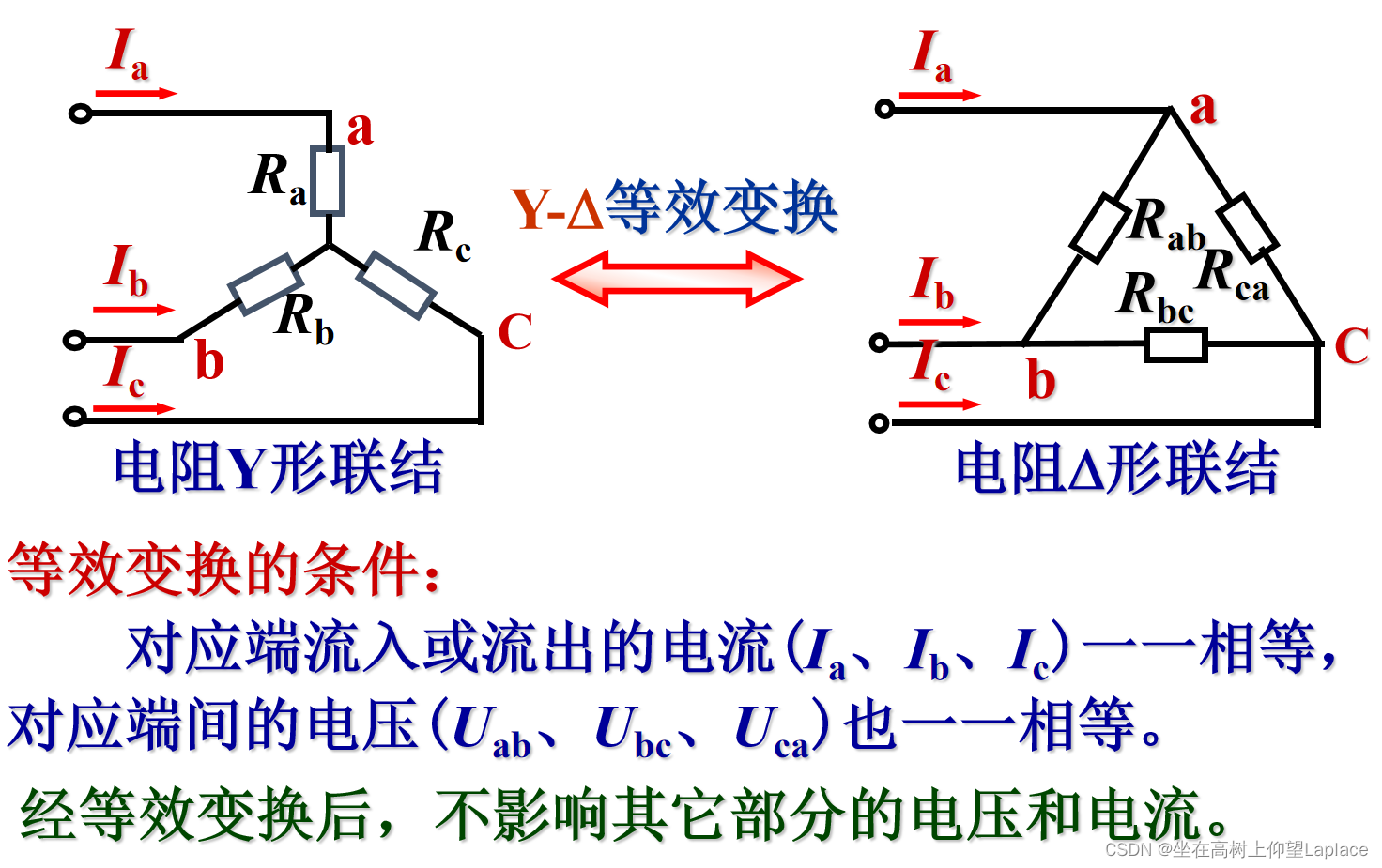
4、电阻星形联结与三角形联结的等换
为什么会有这种变换呢?
- 适用于电桥不平衡的情况
上面公式重点看右边的
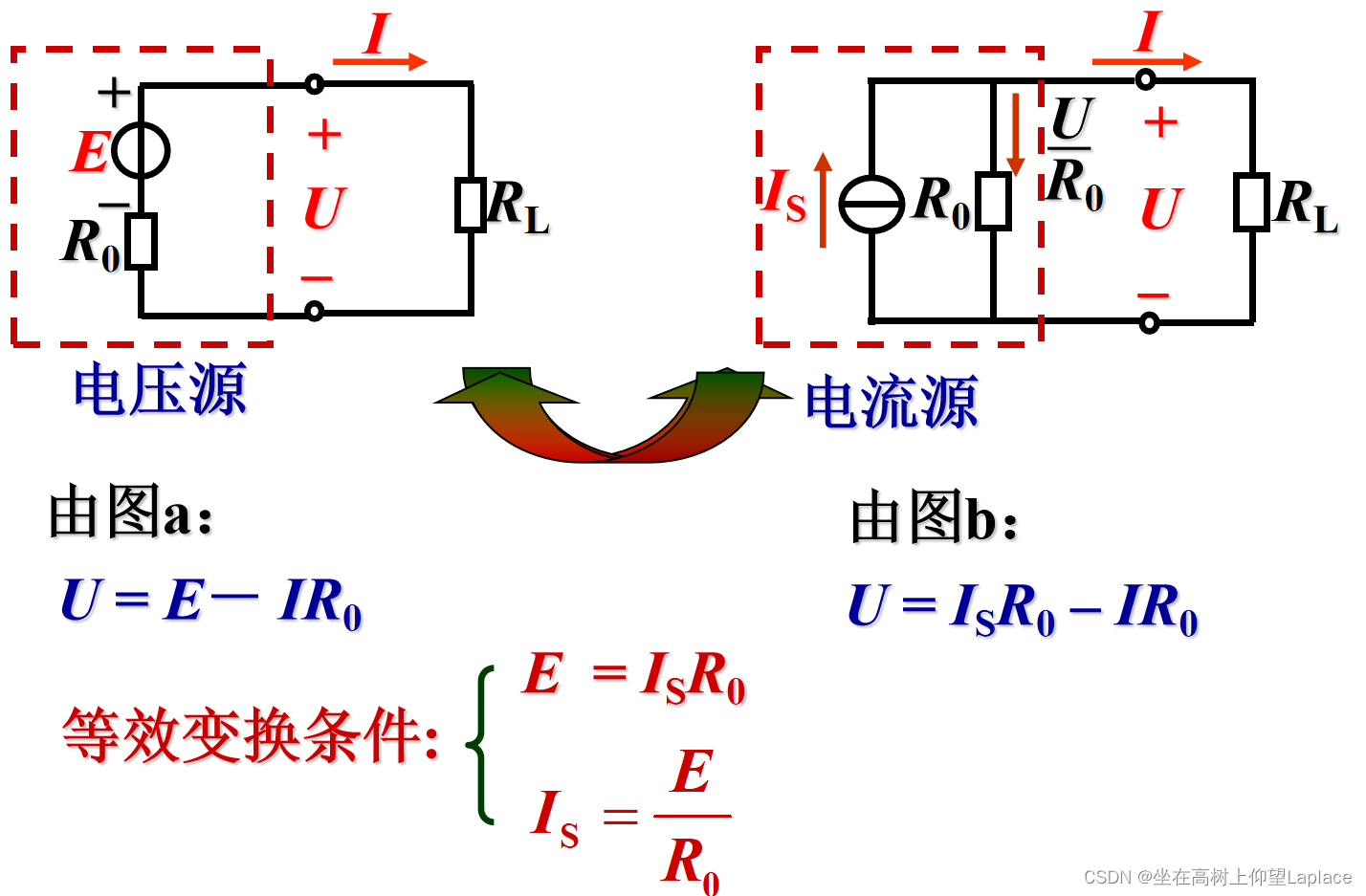
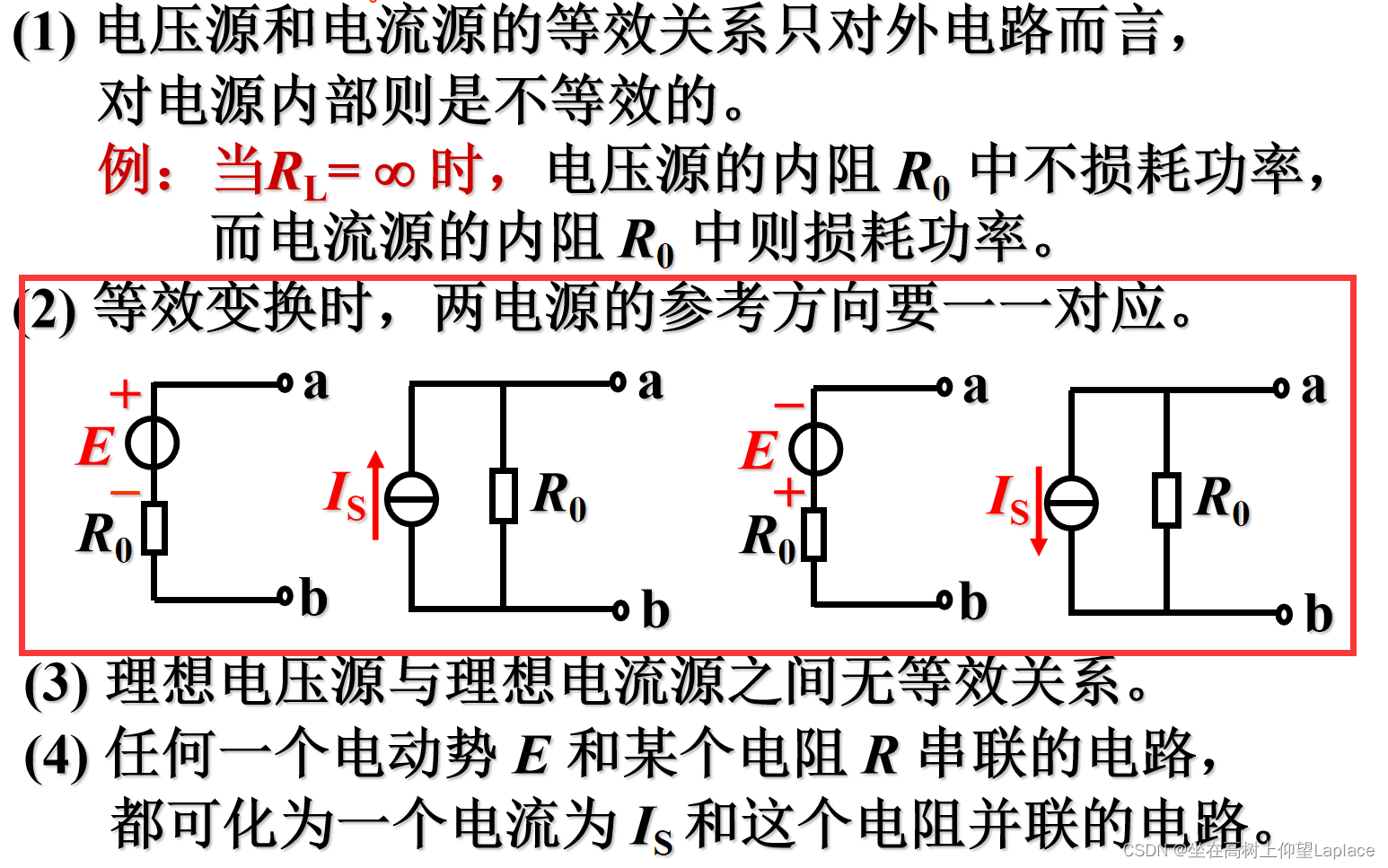
二、电源两种模型的等效变换
将电压源与电流源的外特性曲线拟合,得出等效变换条件。
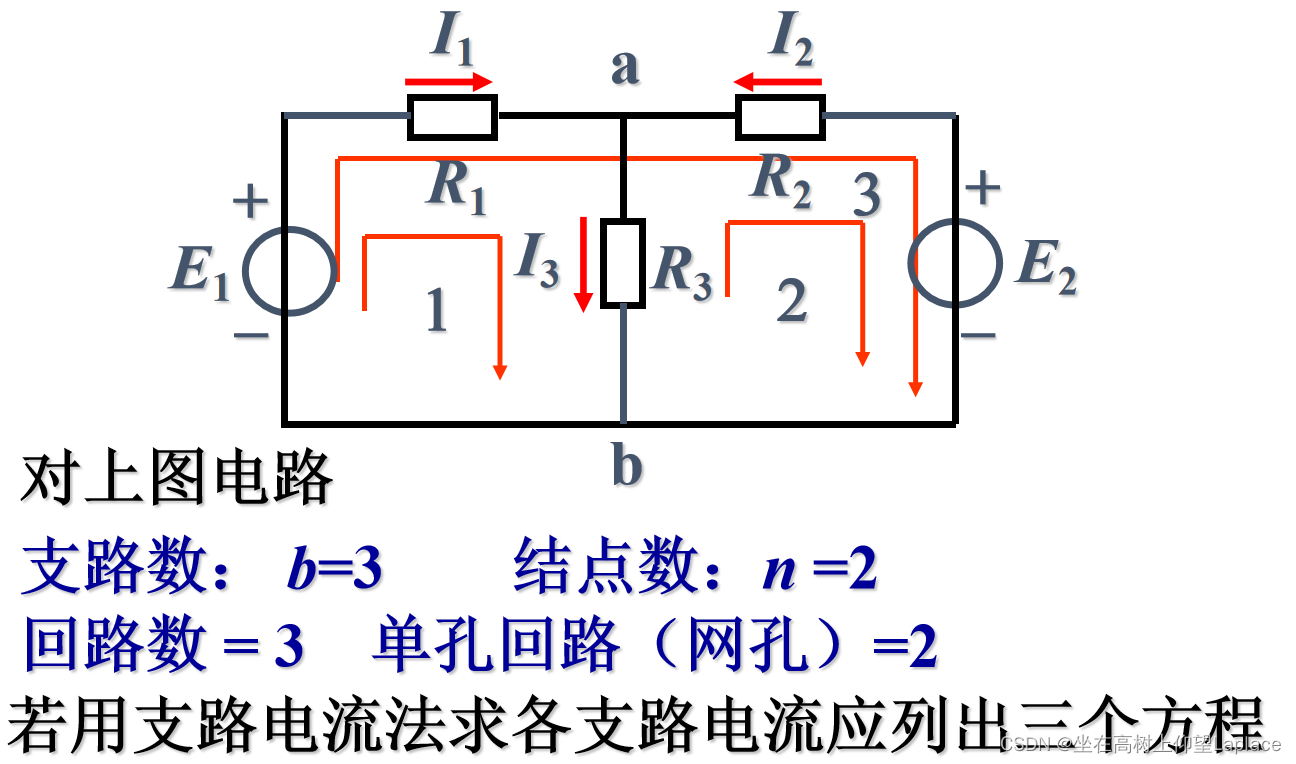
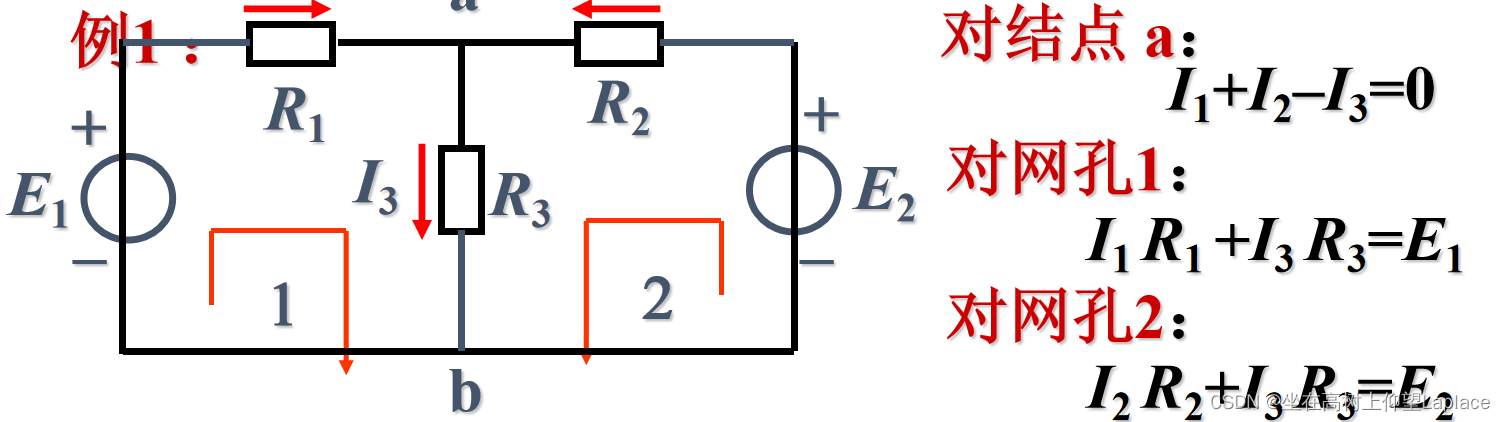
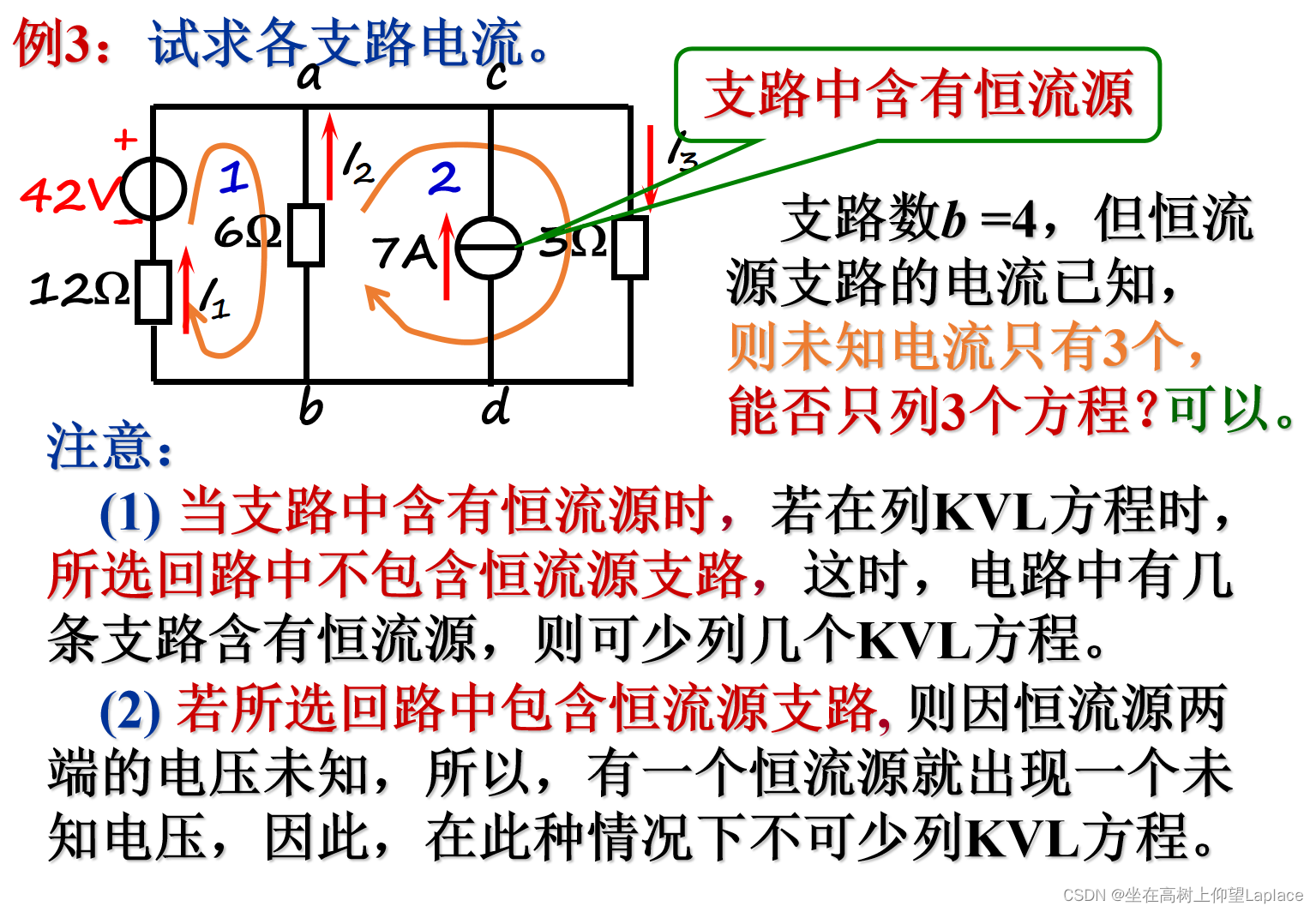
三、支路电流法
支路电流法:以支路电流为未知量、应用基尔霍夫定律(KCL、KVL)列方程组求解。
解题步骤:
- 在图中标出各支路电流的参考方向,对选定的回路,标出回路的循行方向。
- 应用 KCL 对结点列出 ( n-1 )个独立的结点电流方程。
- 应用 KVL 对回路列出 b-( n-1 ) 个独立的回路电压方程(通常可取网孔列出)。
- 联立求解 b 个方程,求出各支路电流。
支路电流法是电路分析中最基本的方法之一,但当支路数较多时,所需方程的个数较多,求解不方便 。
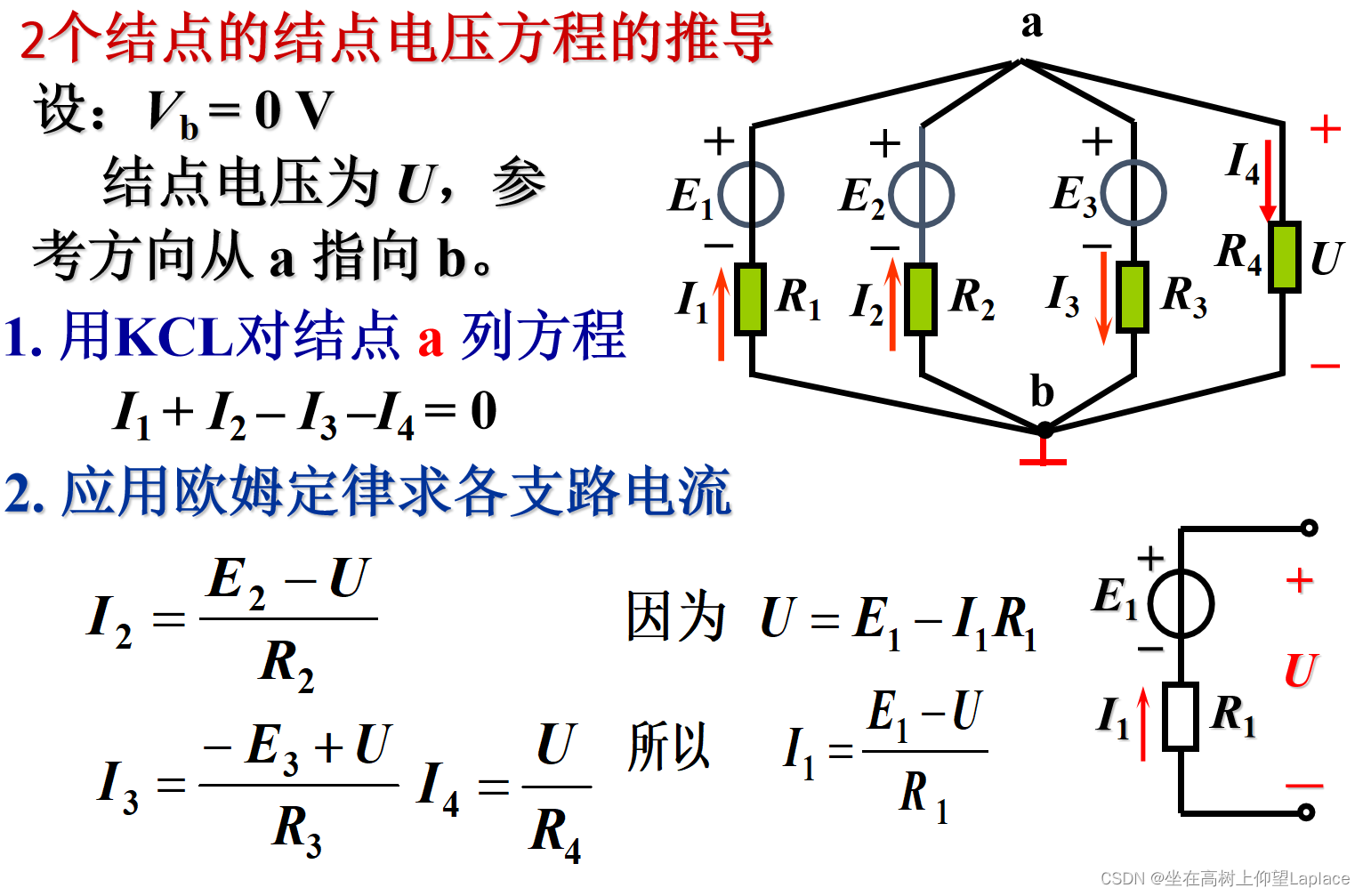
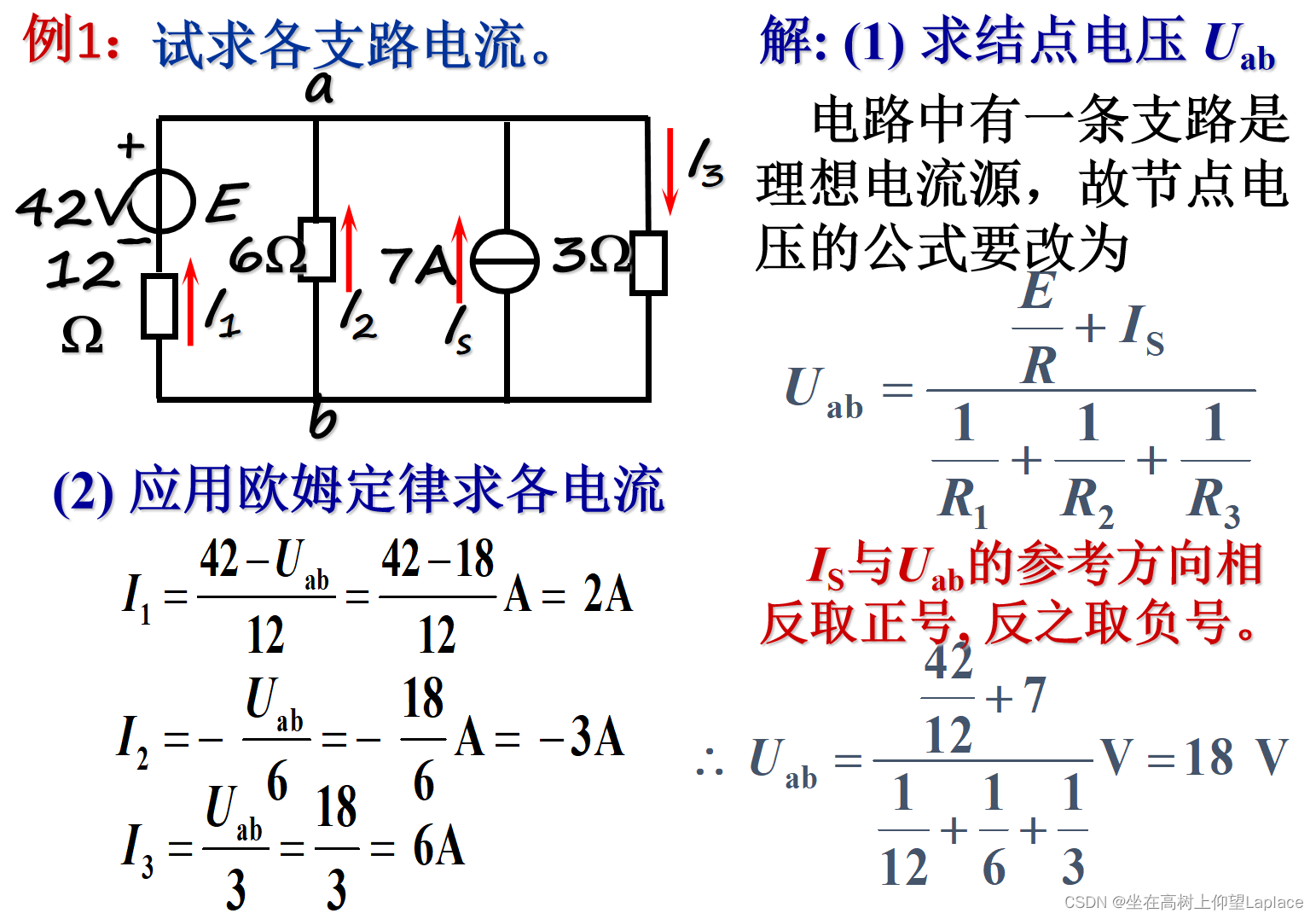
四、结点电压法
- 概念
任选电路中某一结点为零电位参考点(用
表示),其它各结点对参考点的电压,称为结点 电压。
- 方向
结点电压的参考方向从结点指向参考结点
- 求法
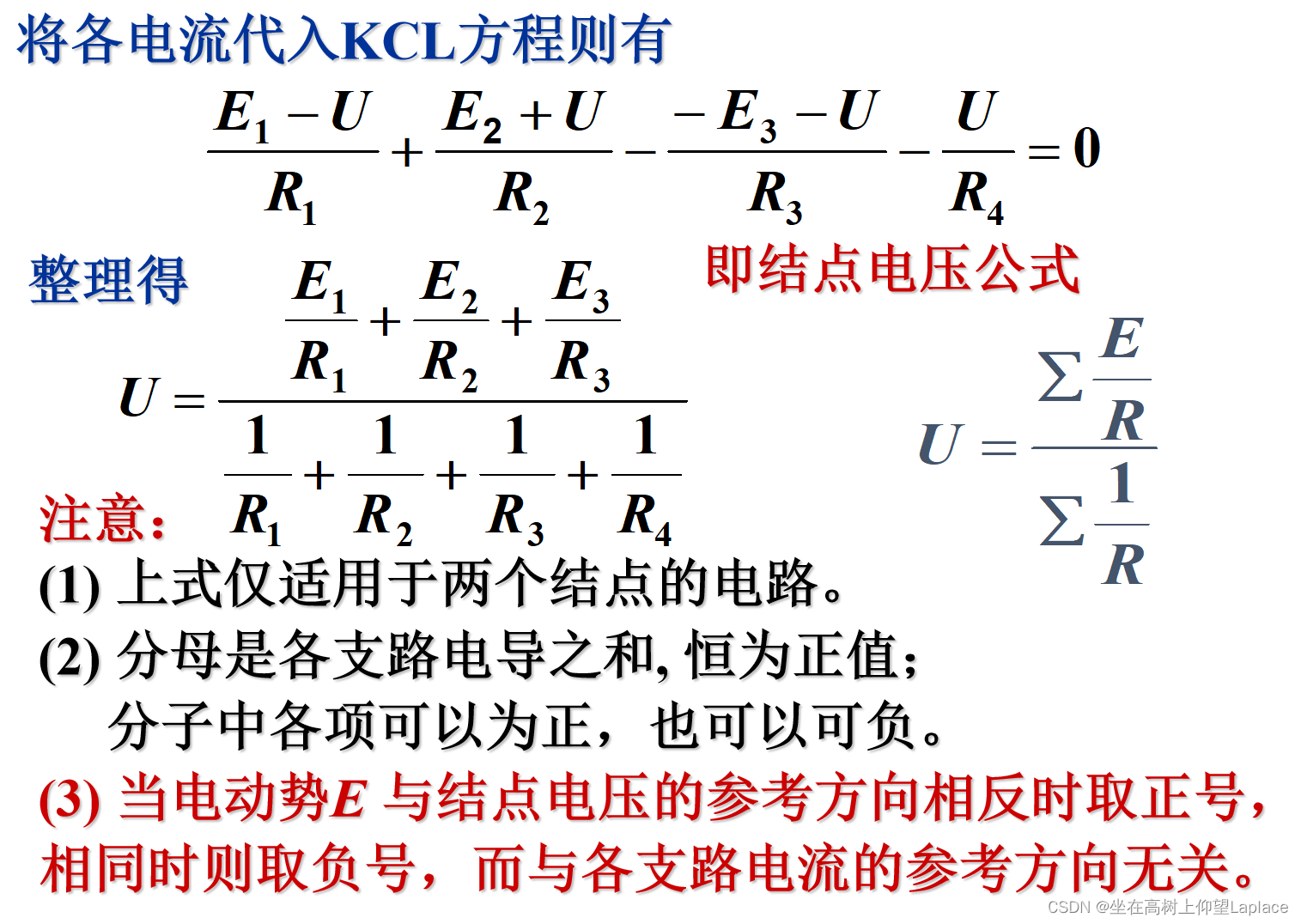
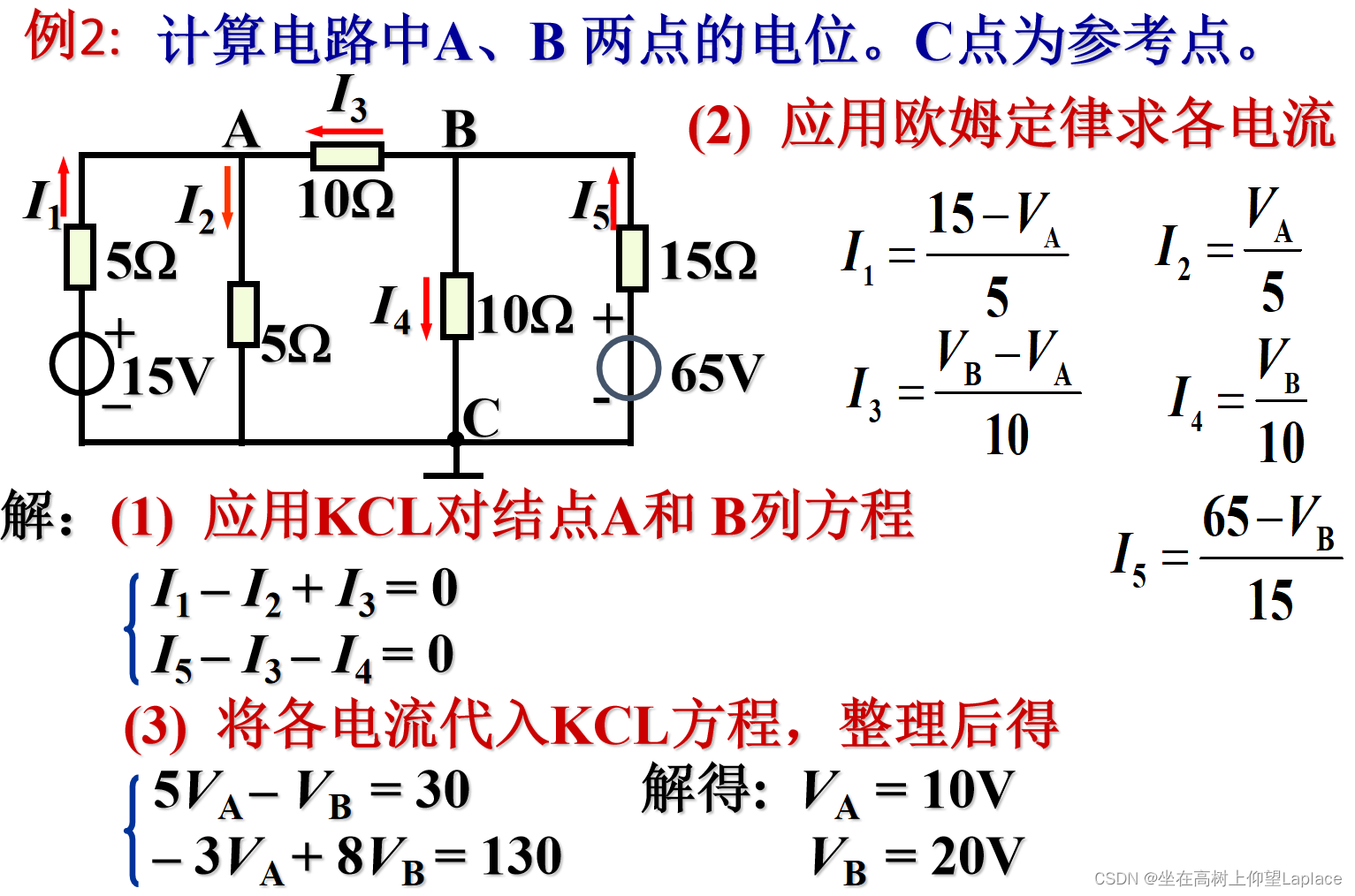
结点电压法:以结点电压为未知量,列方程求解。在求出结点电压后,可应用基尔霍夫 定律或欧姆定律求出各支路的电流或电压。
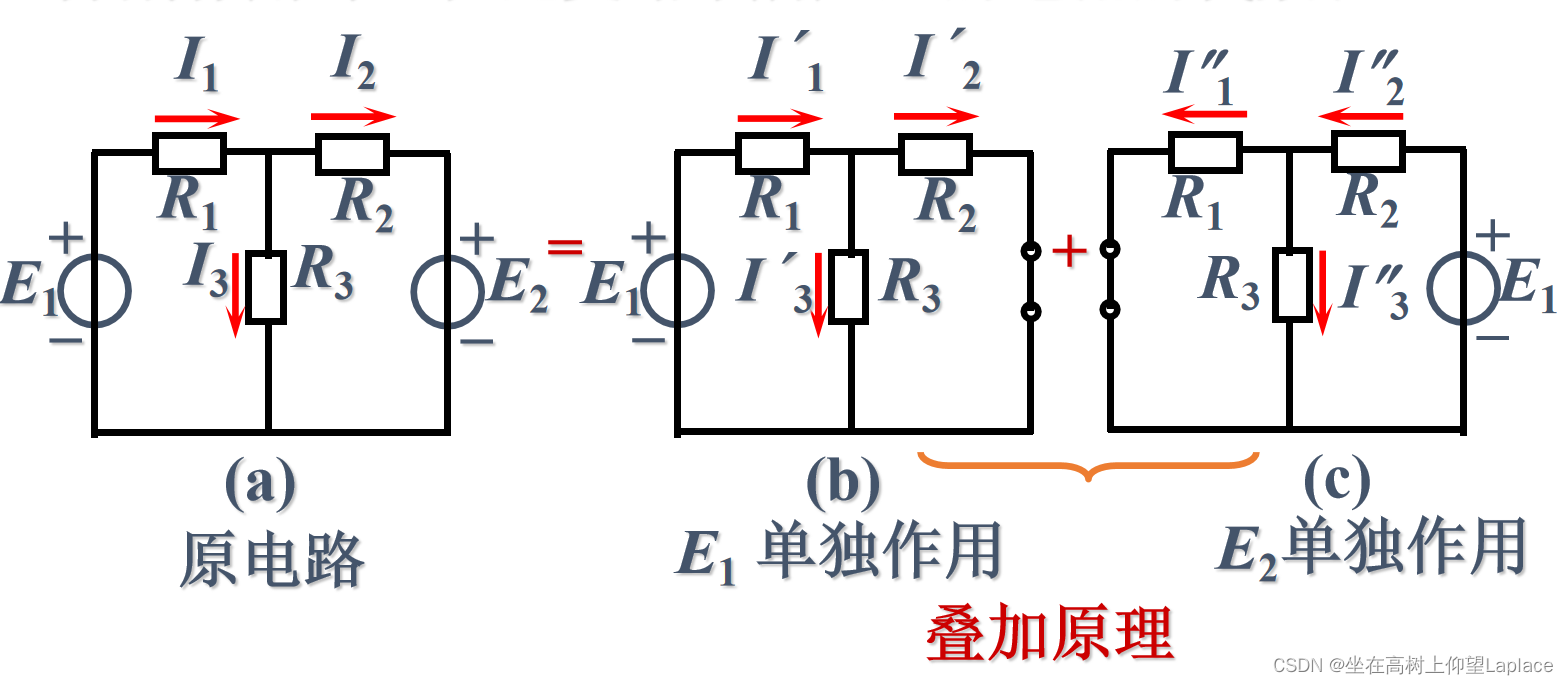
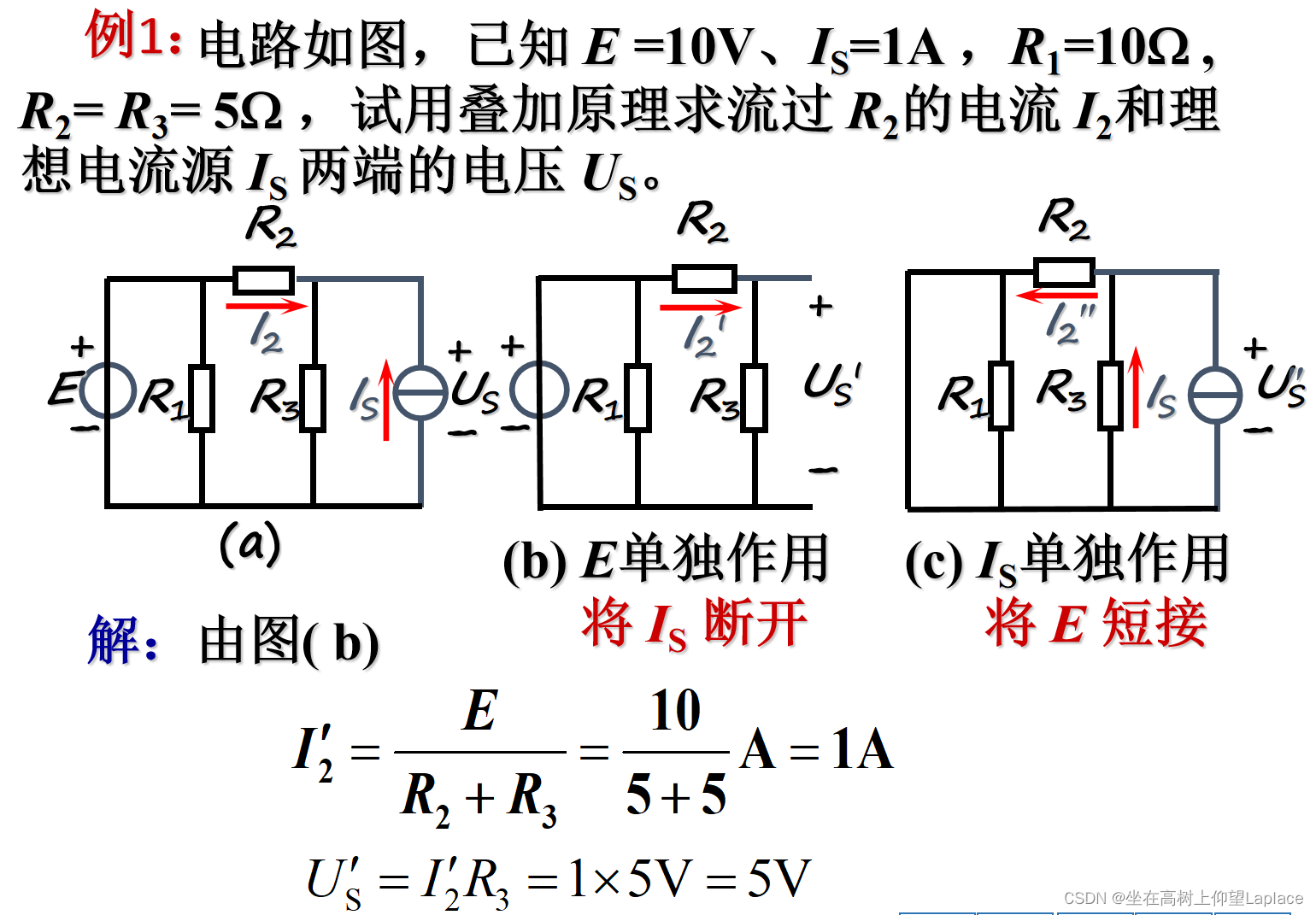
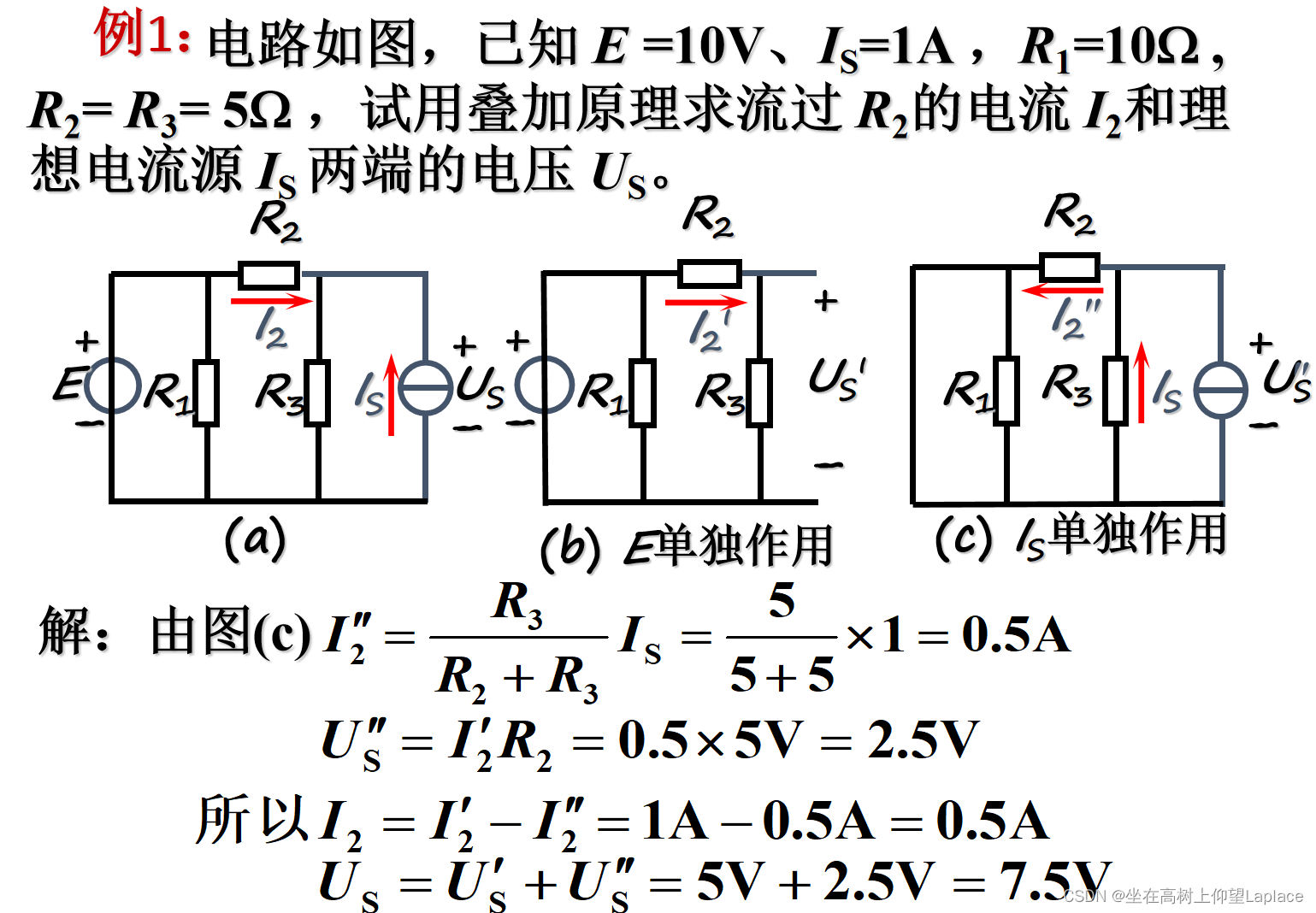
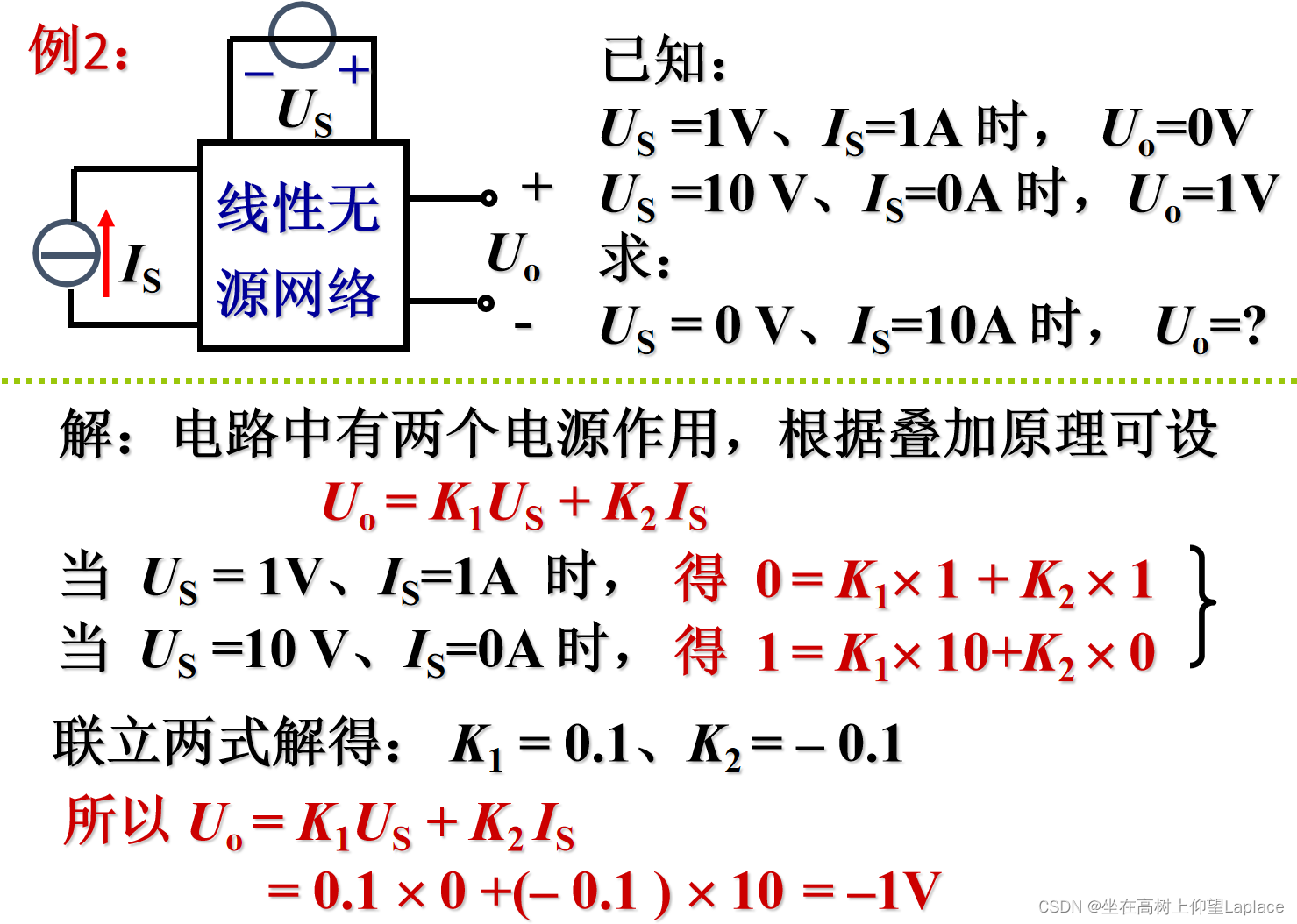
五、叠加原理
- 概念
对于线性电路,任何一条支路的电流,都可以看成是由电路中各个电源(电压源或电流源)分别作用时,在此支路中所产生的电流的代数和。
电压源短路,电流源开路
【补充】齐性定理
只有一个电源作用的线性电路中,各支路的电压或电流和电源成正比
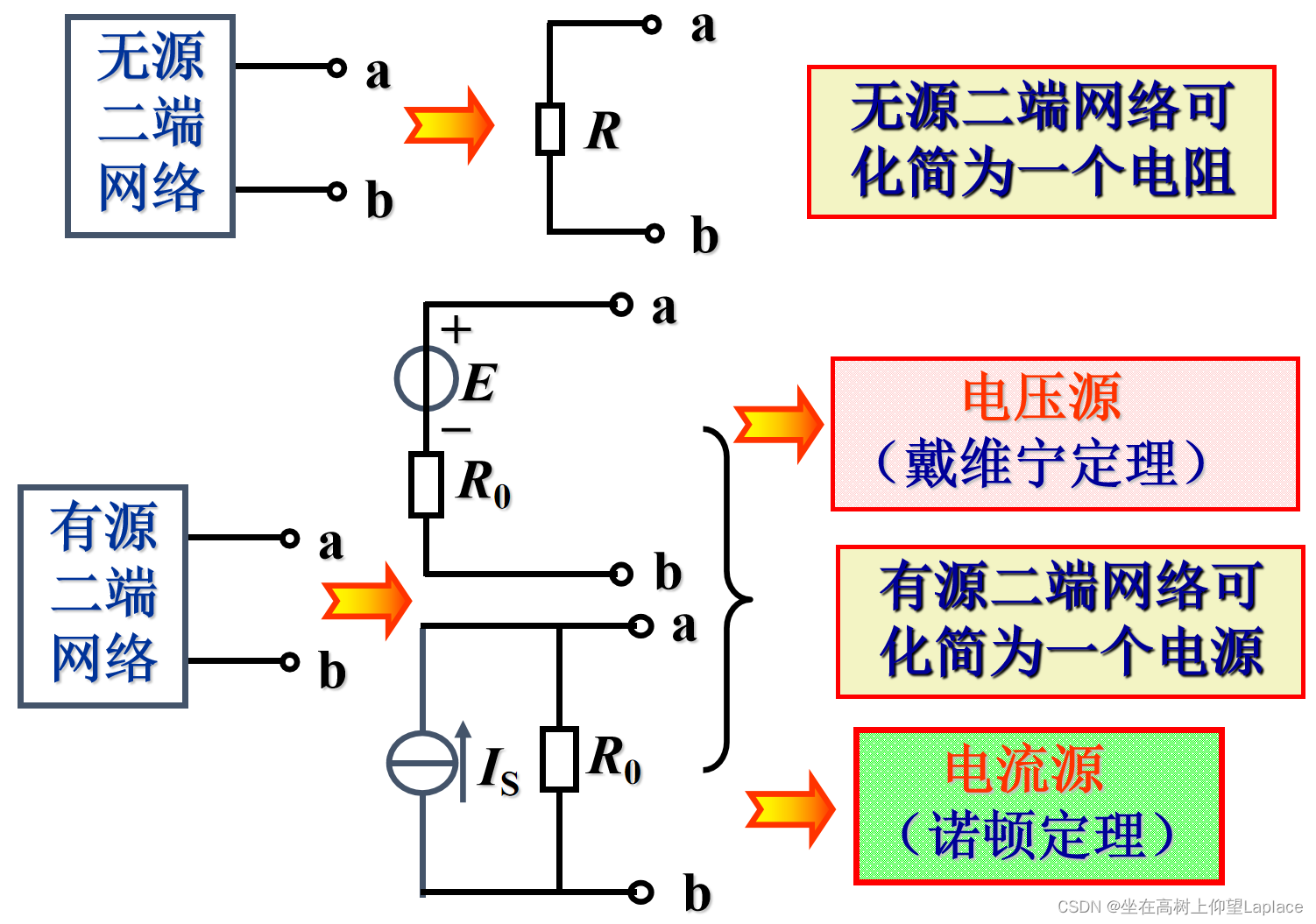
六、等效电源定理
- 有源与无源
1、戴维南定理
- 概念
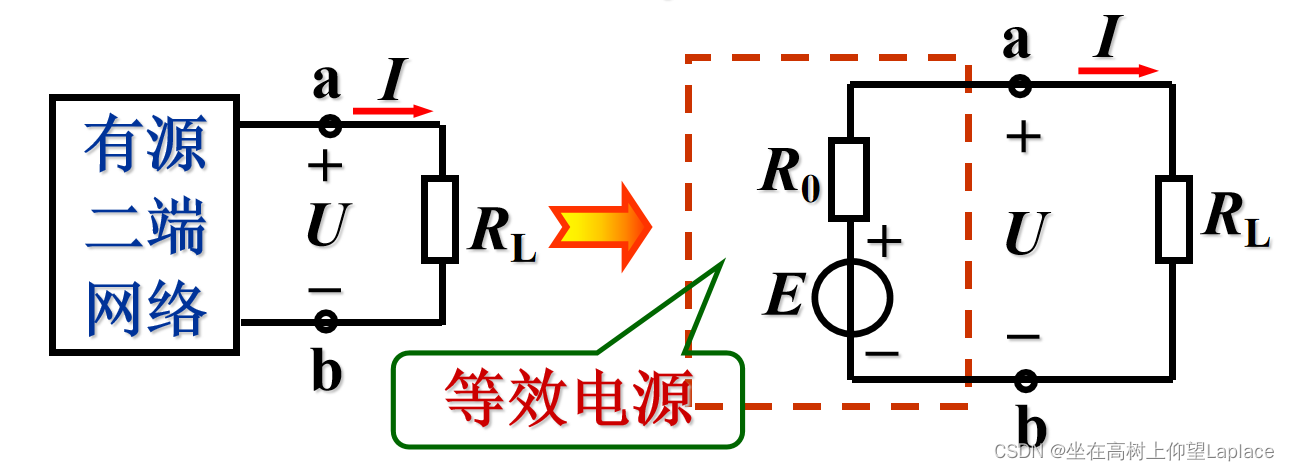
任何一个有源二端线性网络都可以用一个电动势为E的理想电压源和内阻 R0 串联的电源来等效代替
- 内容
等效电源的电动势E 就是有源二端网络的开路电压U0,即将负载断开后 a 、b两端之间的电压。 等效电源的内阻R0等于有源二端网络中所有电源均除去(理想电压源短路,理想电流源开路)后所得到的无源二端网络 a 、b两端之间的等效电阻。
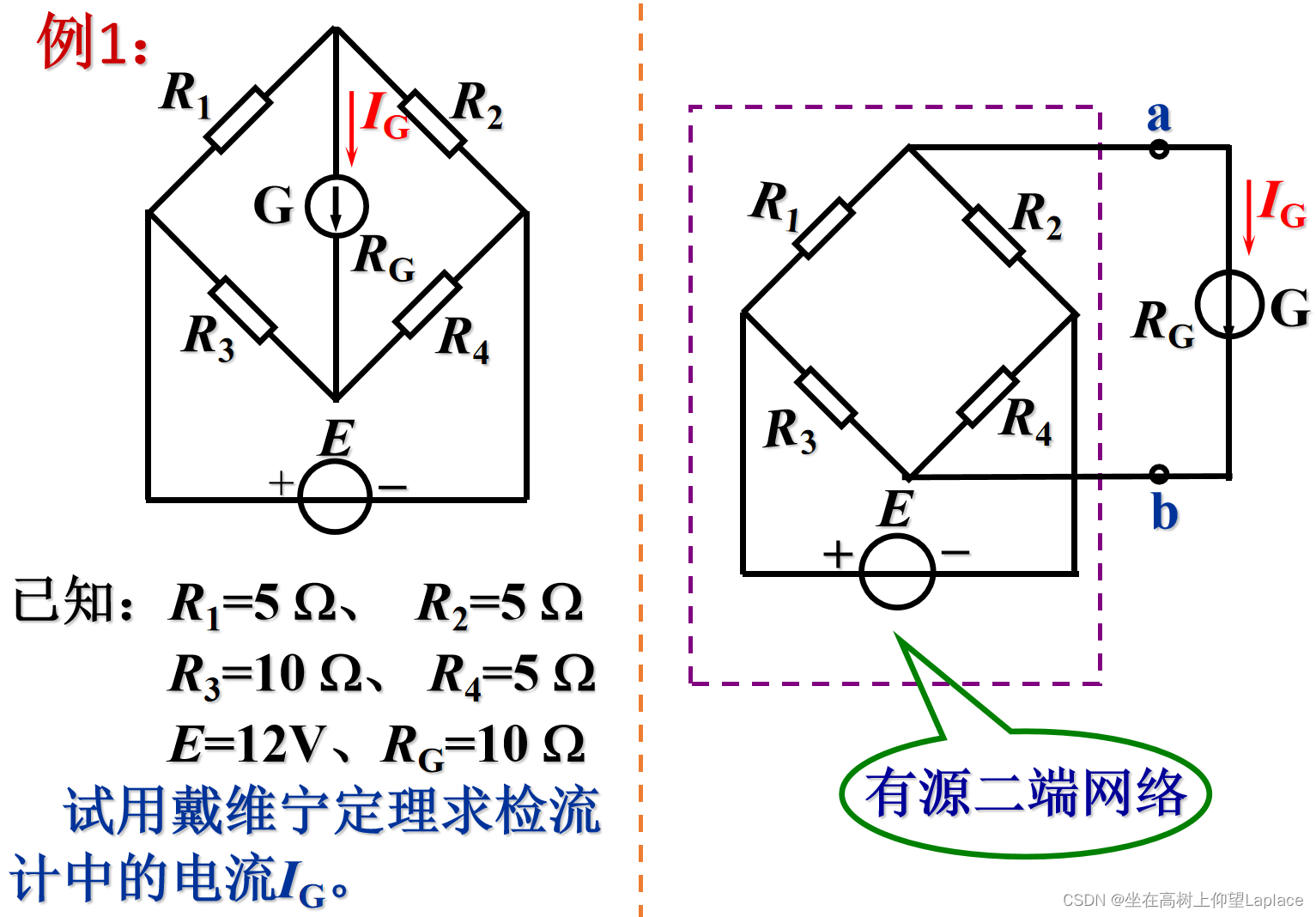
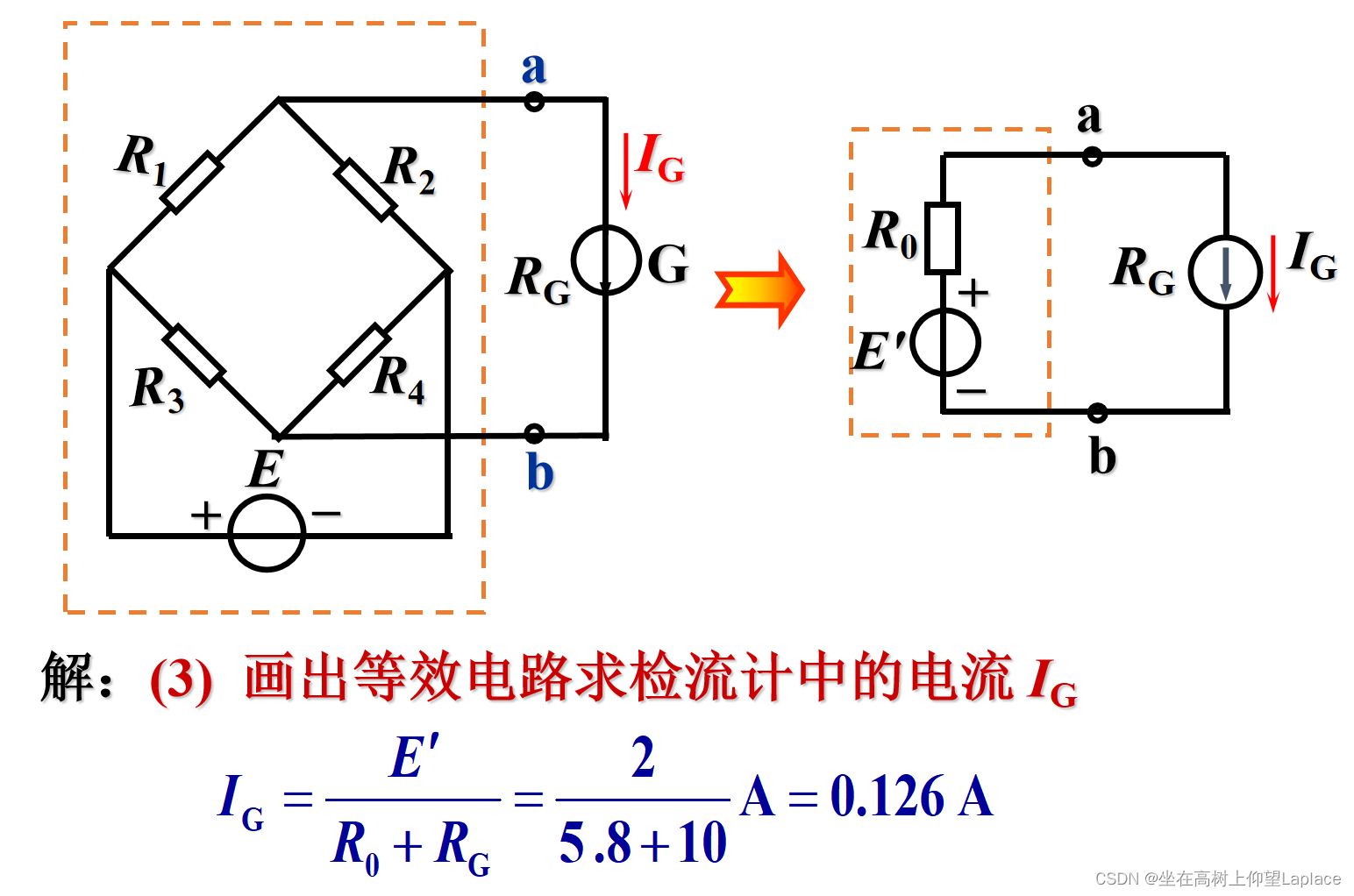
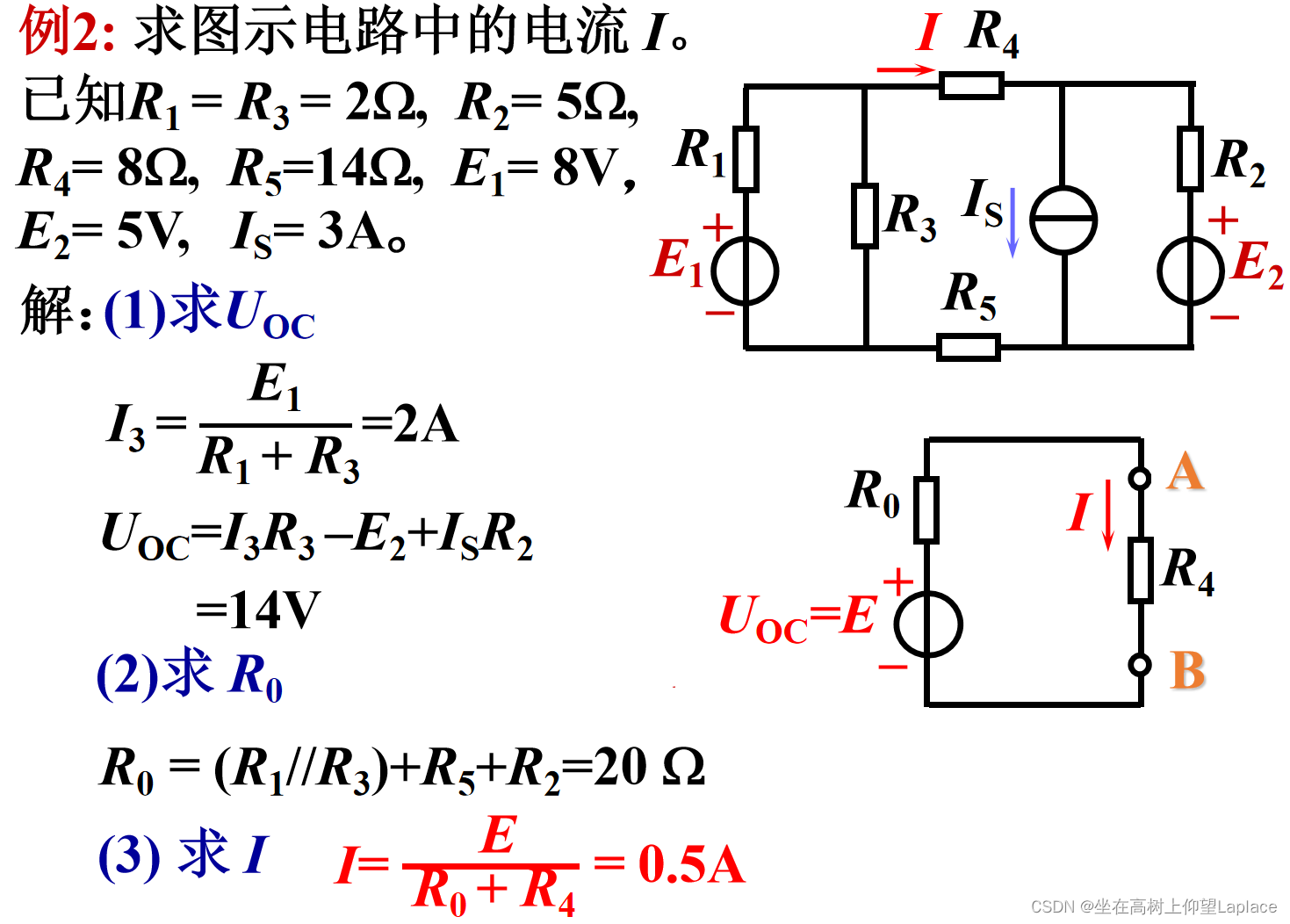
- 练习
2、诺顿定理
- 概念
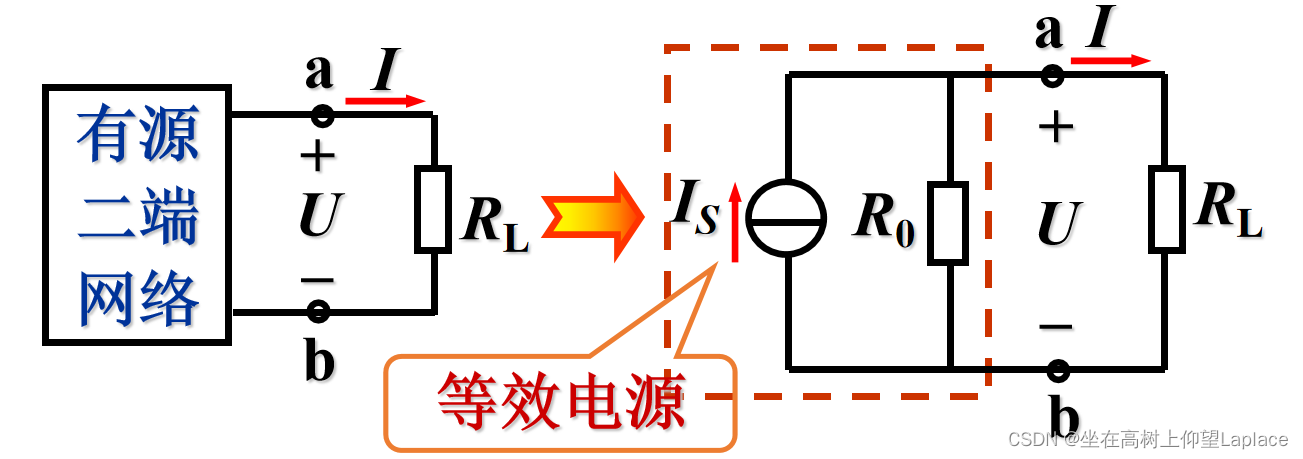
任何一个有源二端线性网络都可以用一个电流为IS的理想电流源和内阻 R0 并联的电源来等效代替
- 内容
等效电源的电流 IS 就是有源二端网络的短路电流,即将 a 、b两端短接后其中的电流。等效电源的内阻R0等于有源二端网络中所有电源均除去(理想电压源短路,理想电流源开路)后所得到的无源二端网络 a 、b两端之间的等效电阻。
七、课后习题
1、等效变换问题
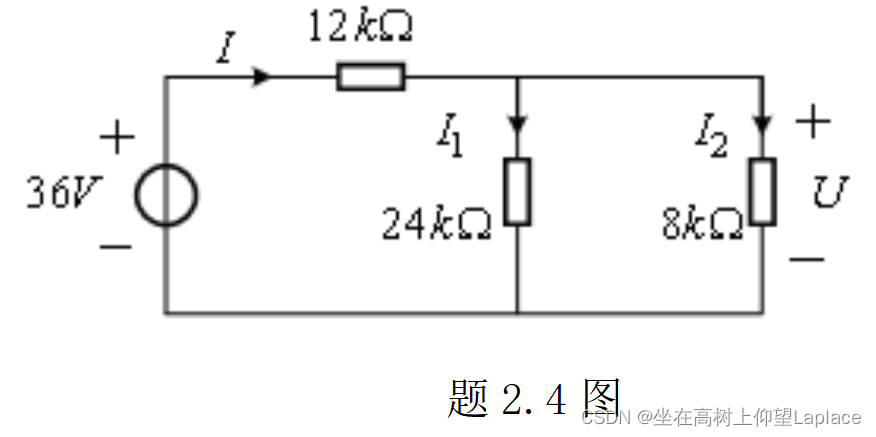
用等效变换的方法计算题2.4图所示电路中的电流
、
、
和电压U
2、化简电路问题
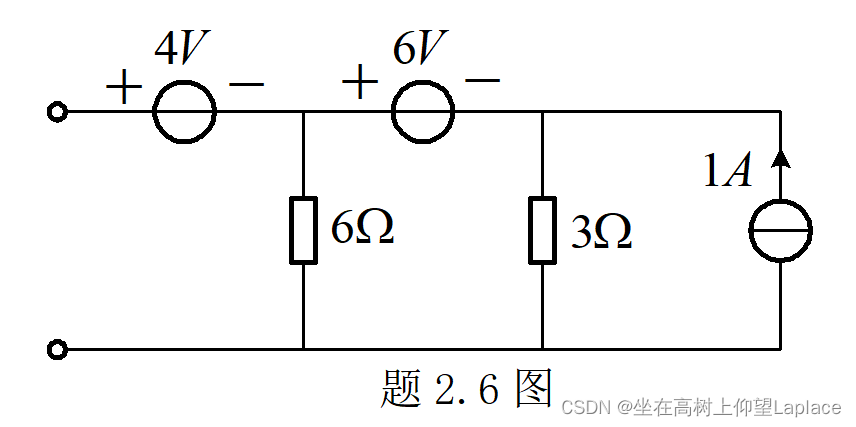
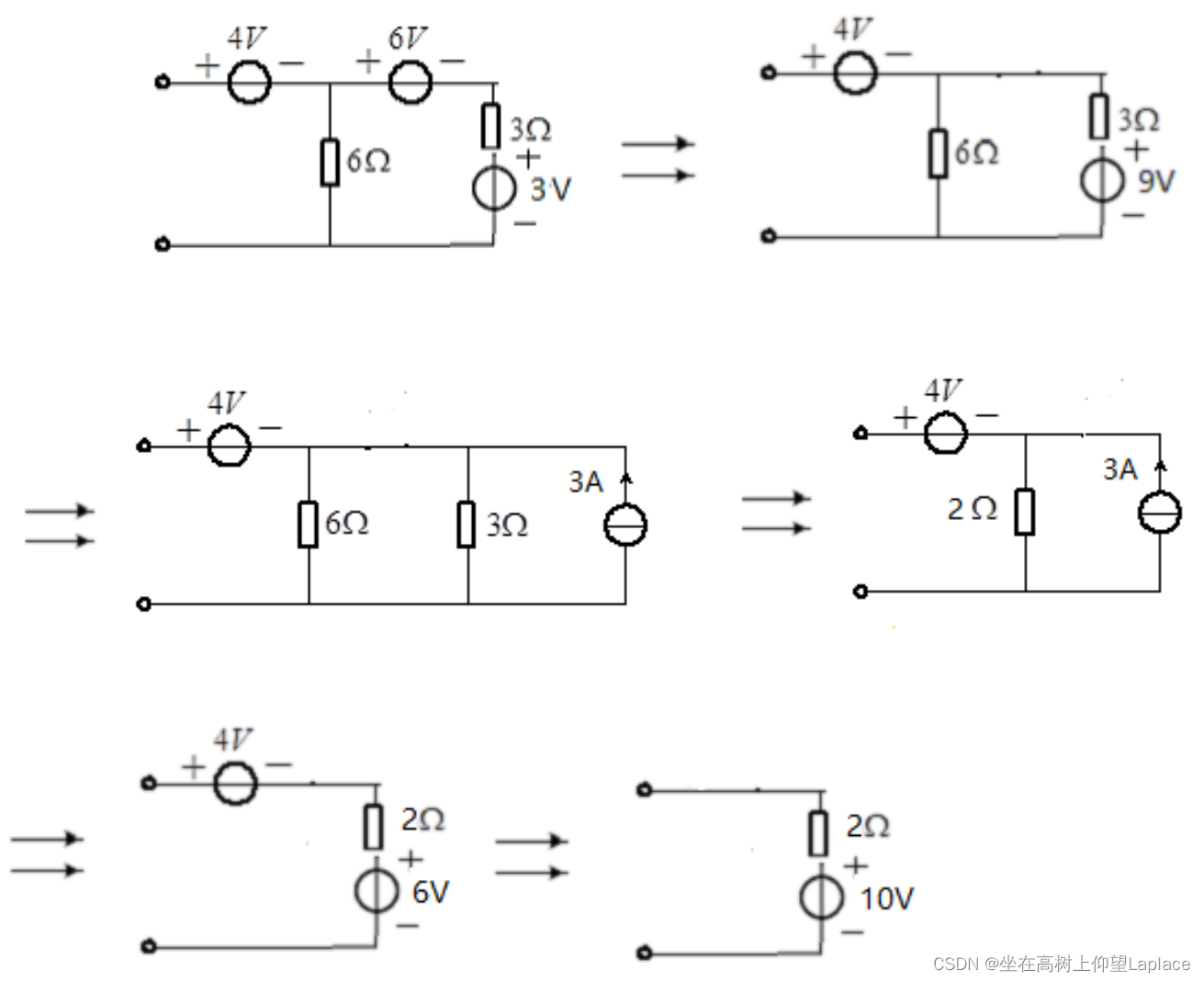
试化简题2.6图所示的有源二端网络
解:
3、功率问题
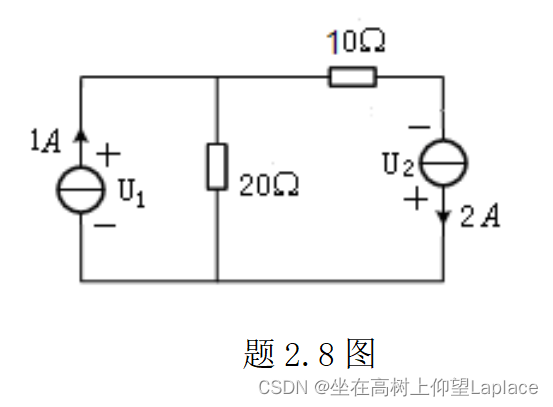
在题2.8图所示的电路中,求各理想电流源的端电压、功率及各电阻上消耗的功率。
4、电流问题
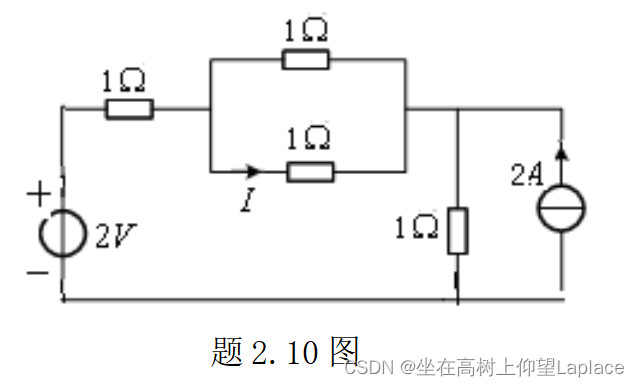
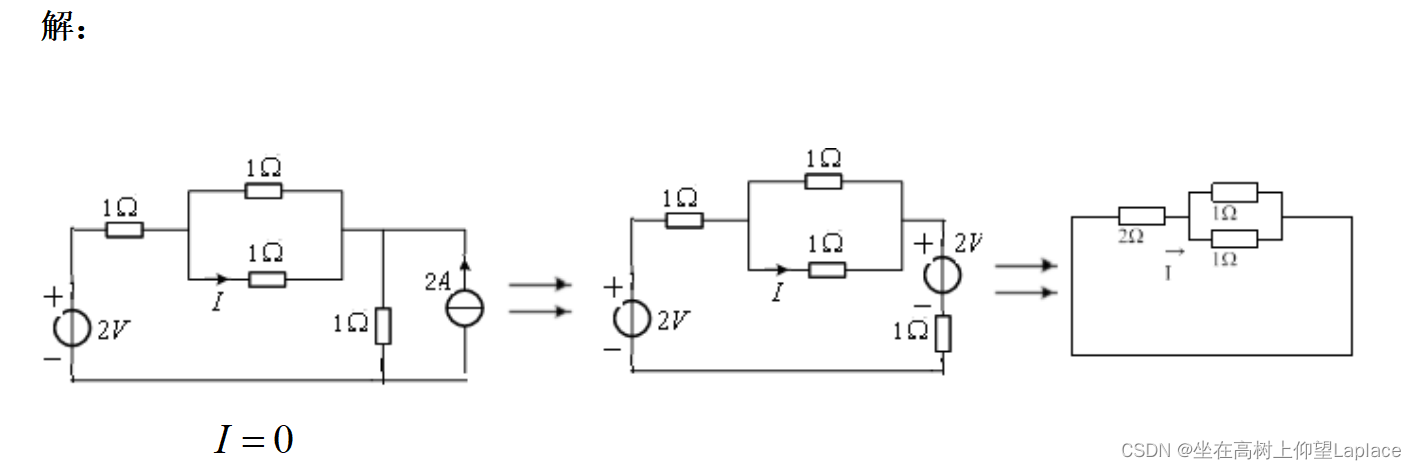
计算题2.10图中的电流
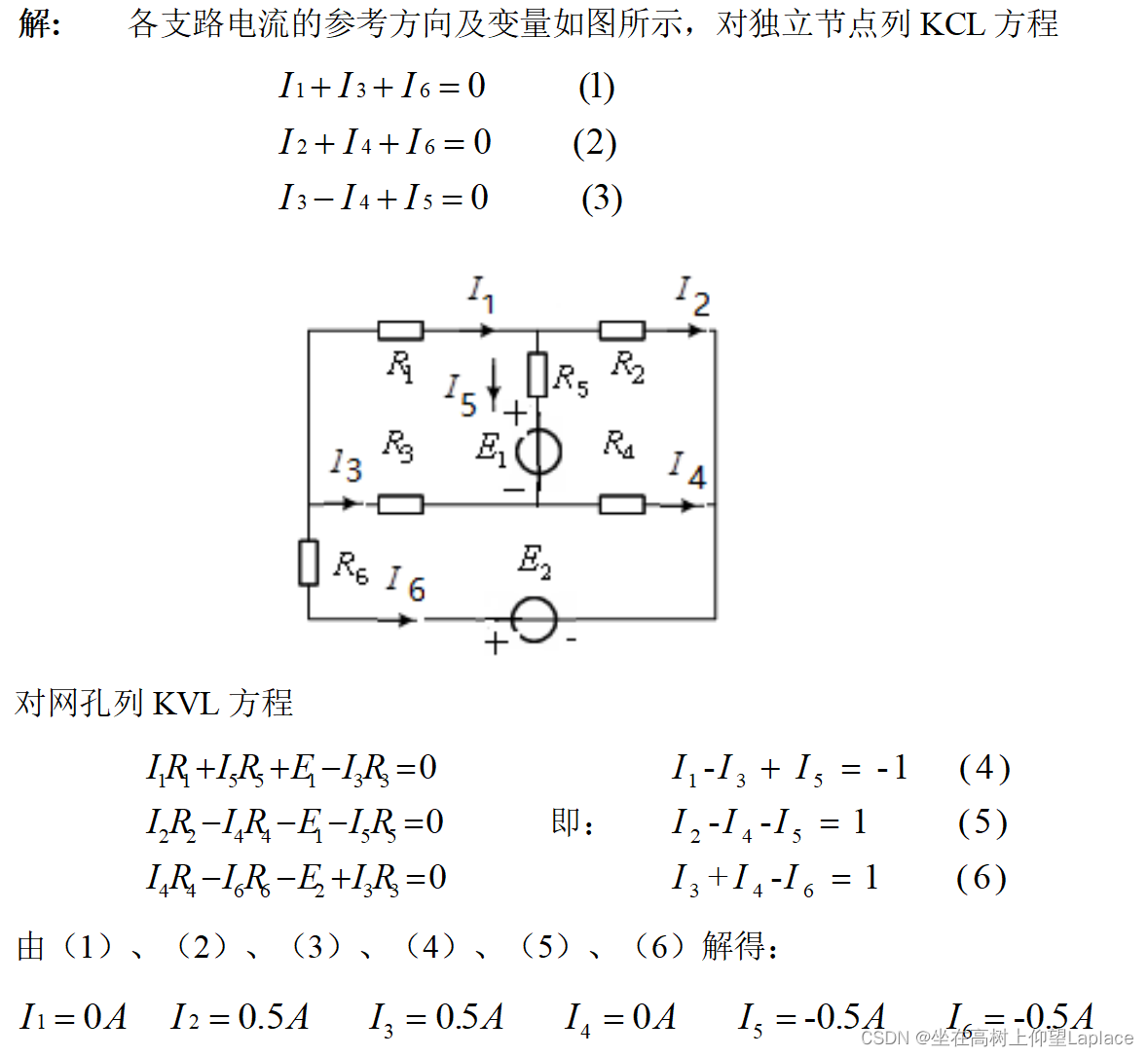
4.1 涉及支路电流法的求支路电路
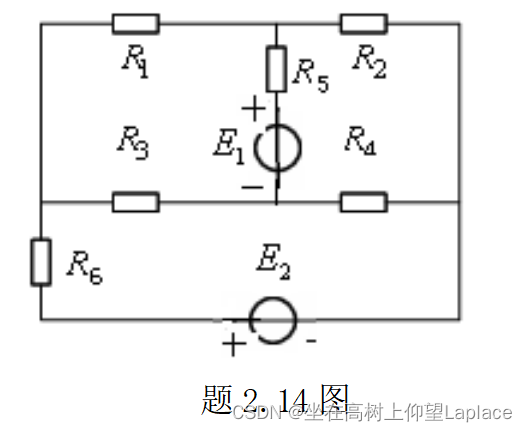
在题2.14图的电路中,已知
,
V。用支路电流法求各支路电流
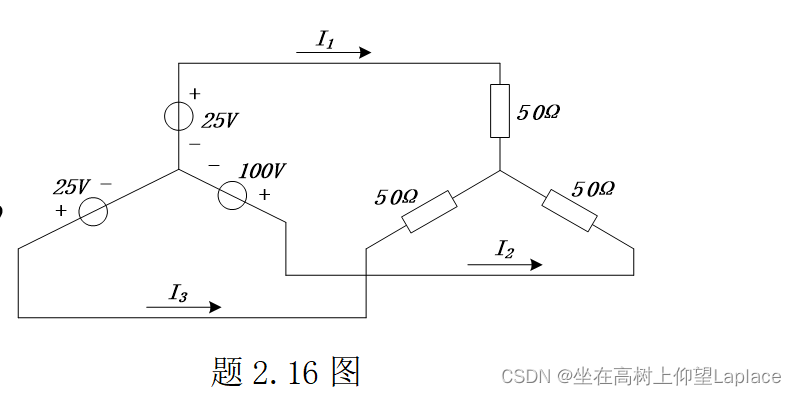
4.2 涉及结点电压法的求支路电流
试用结点电压法,求题2.16图所示电路中的各支路电流。
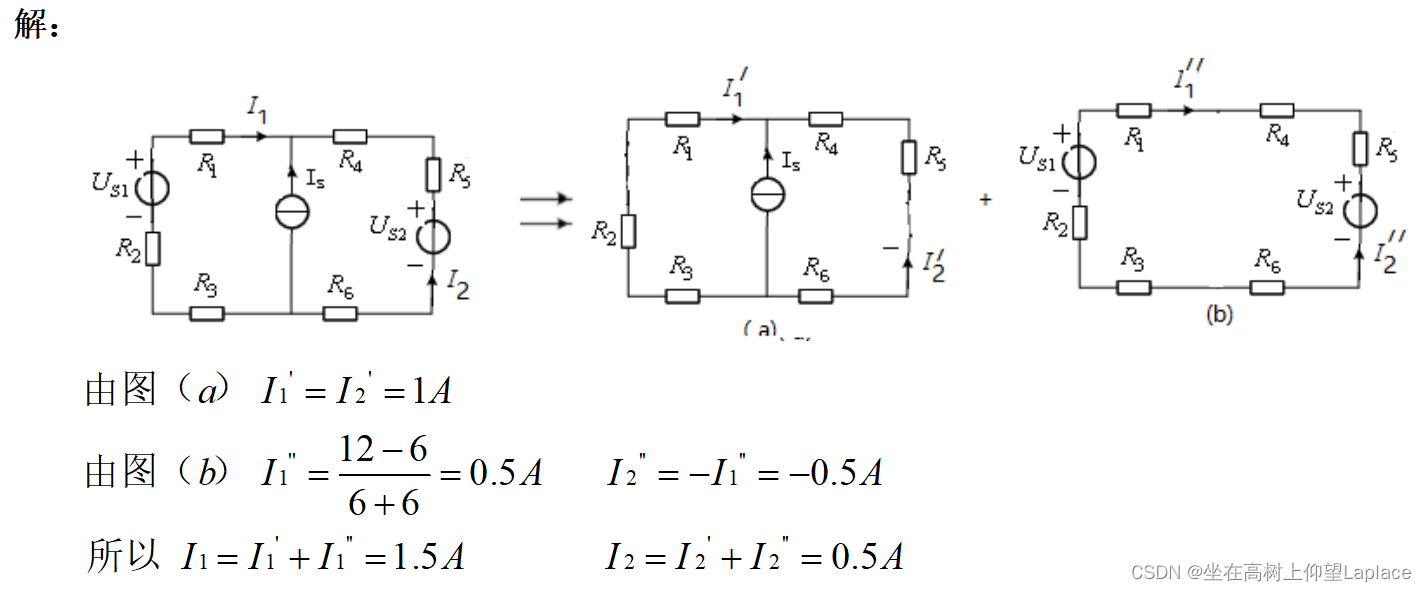
4.3 涉及叠加原理的求支路电流
用叠加定理求题2.13图所示电路中各支路电流
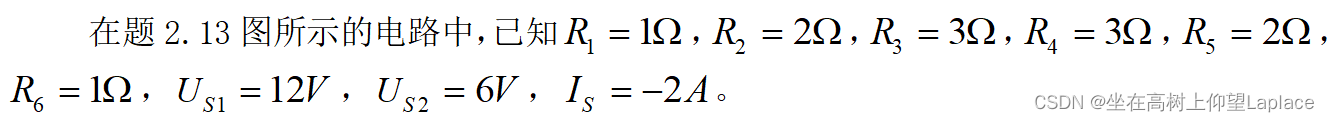
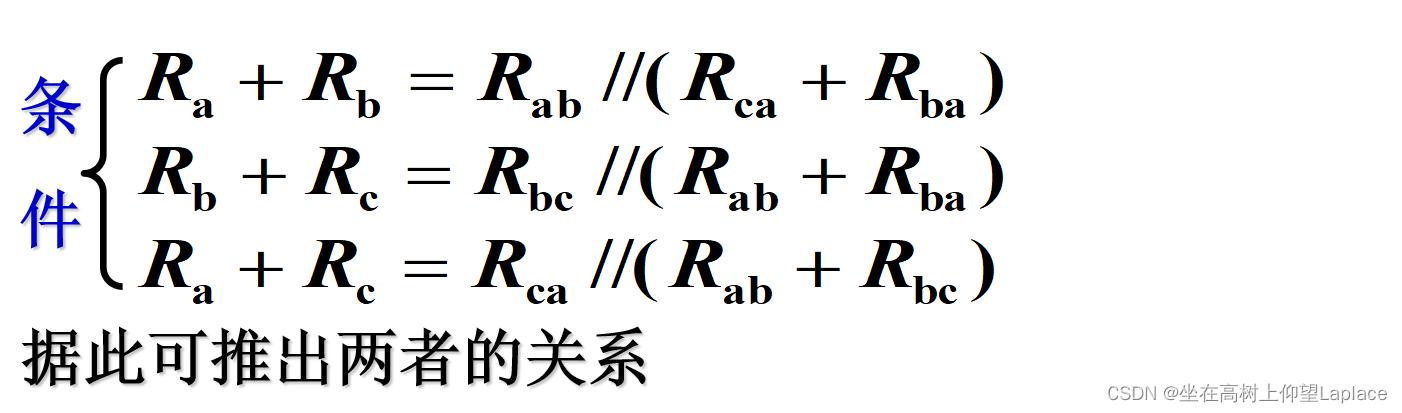
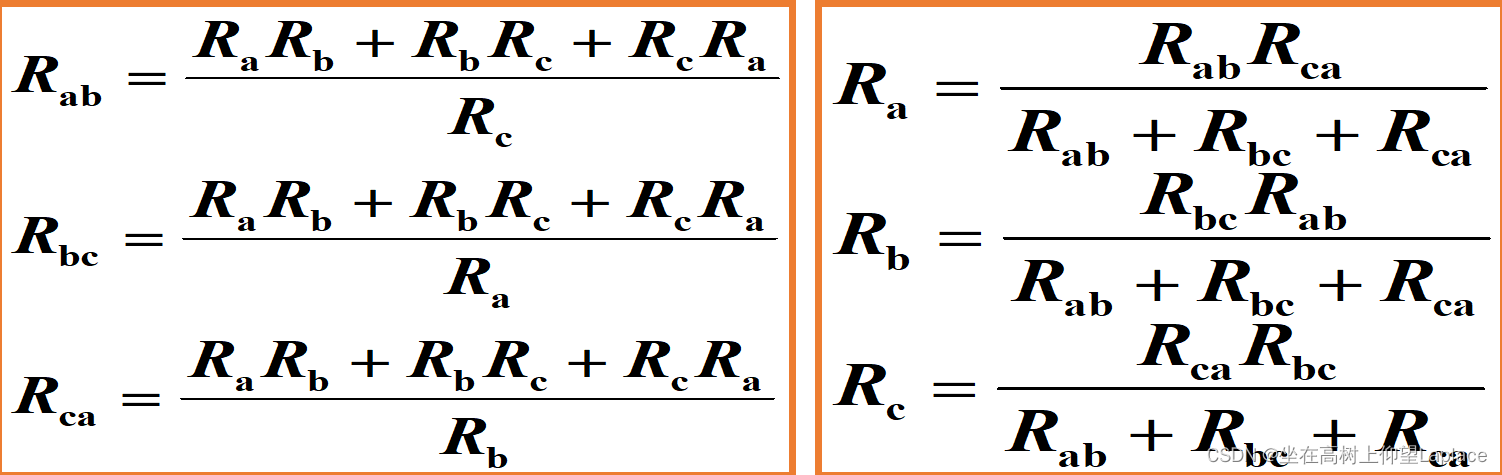
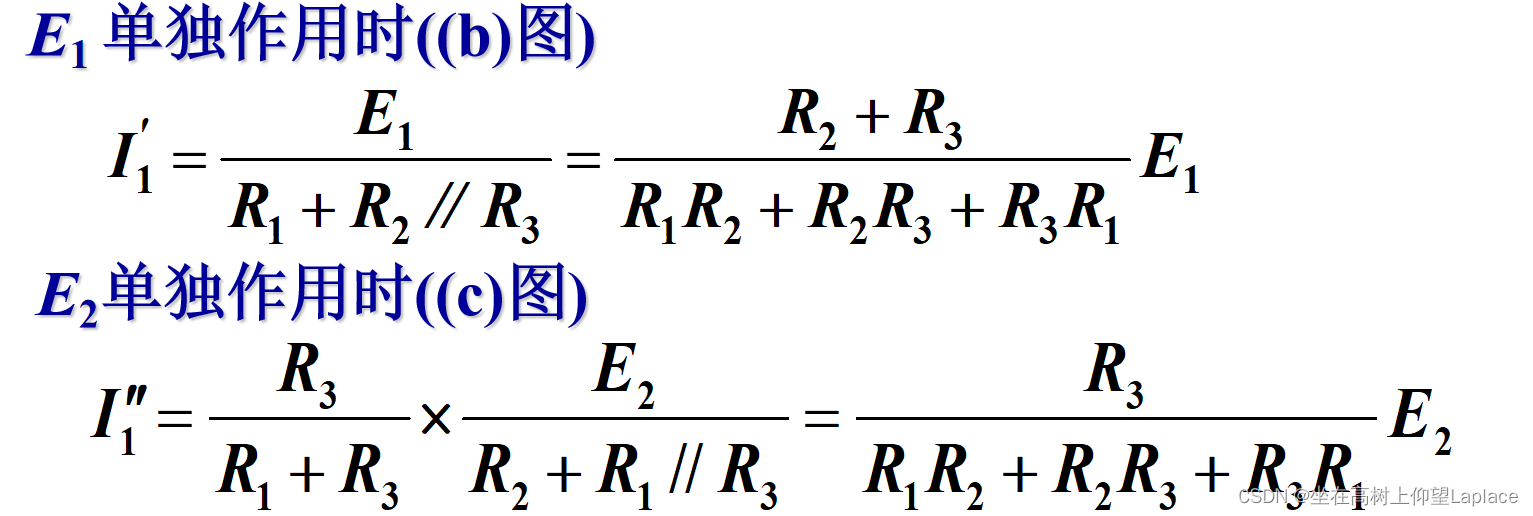
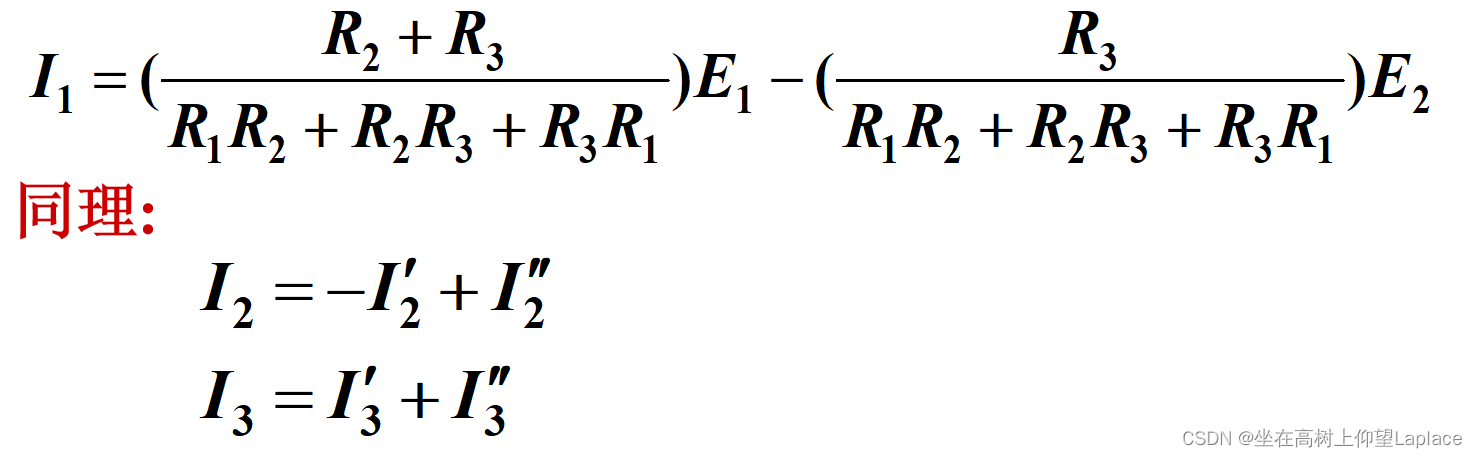



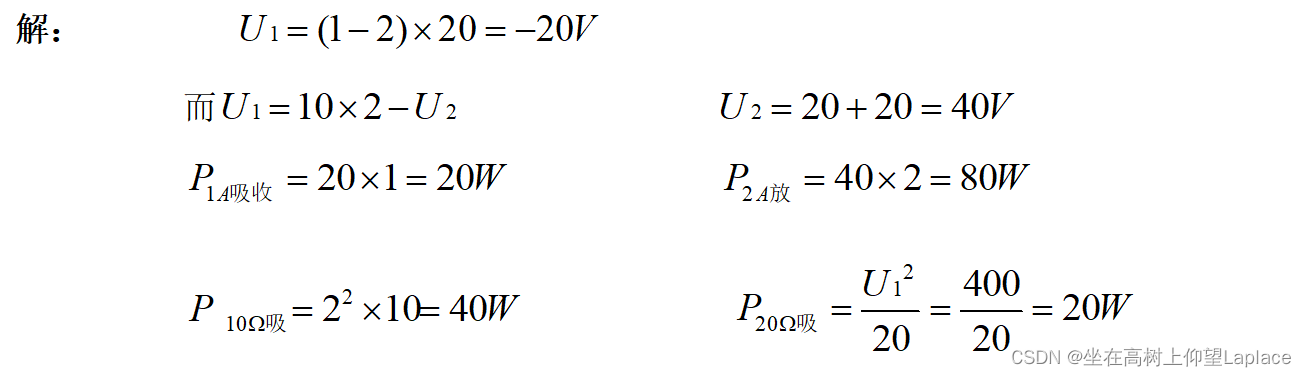
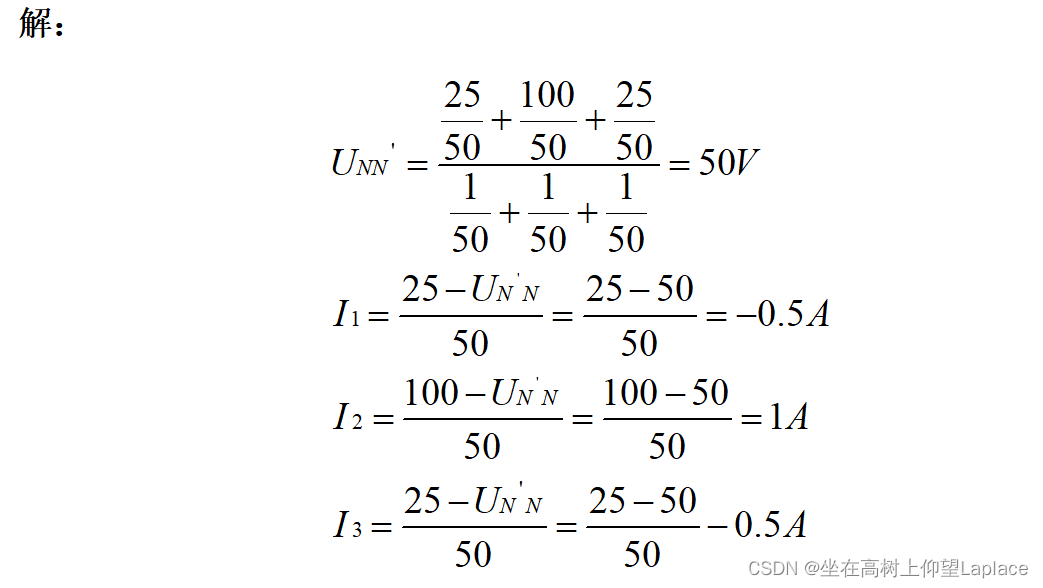




![[附源码]计算机毕业设计springboot学生宿舍维修管理系统](https://img-blog.csdnimg.cn/5e6c1d0ef6fa47bca850f1e9a7551e24.png)