noise type

1. 高斯噪声和泊松噪声

下面公式表示用异方差高斯近似泊松分布：

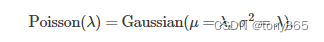
https://people.csail.mit.edu/hasinoff/pubs/hasinoff-photon-2012-preprint.pdf

但是这个在暗光下（极暗，pixel值<2）还是有误差，详细在第2节说明

概率分布与泊松分布、正态分布

http://hongyitong.github.io/2016/11/13/%E4%BA%8C%E9%A1%B9%E5%88%86%E5%B8%83%E3%80%81%E6%B3%8A%E6%9D%BE%E5%88%86%E5%B8%83%E3%80%81%E6%AD%A3%E6%80%81%E5%88%86%E5%B8%83/

2. 高斯分布和泊松分布的差异：

主要参考Gaussian Noise is Added, Poisson Noise is Applied

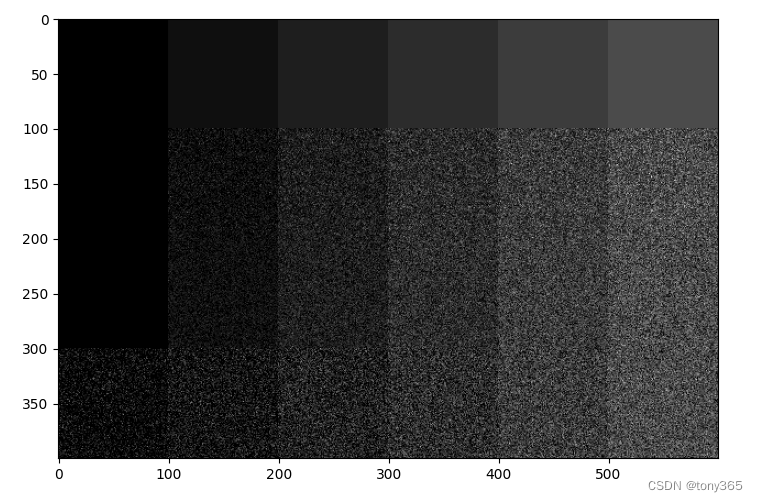
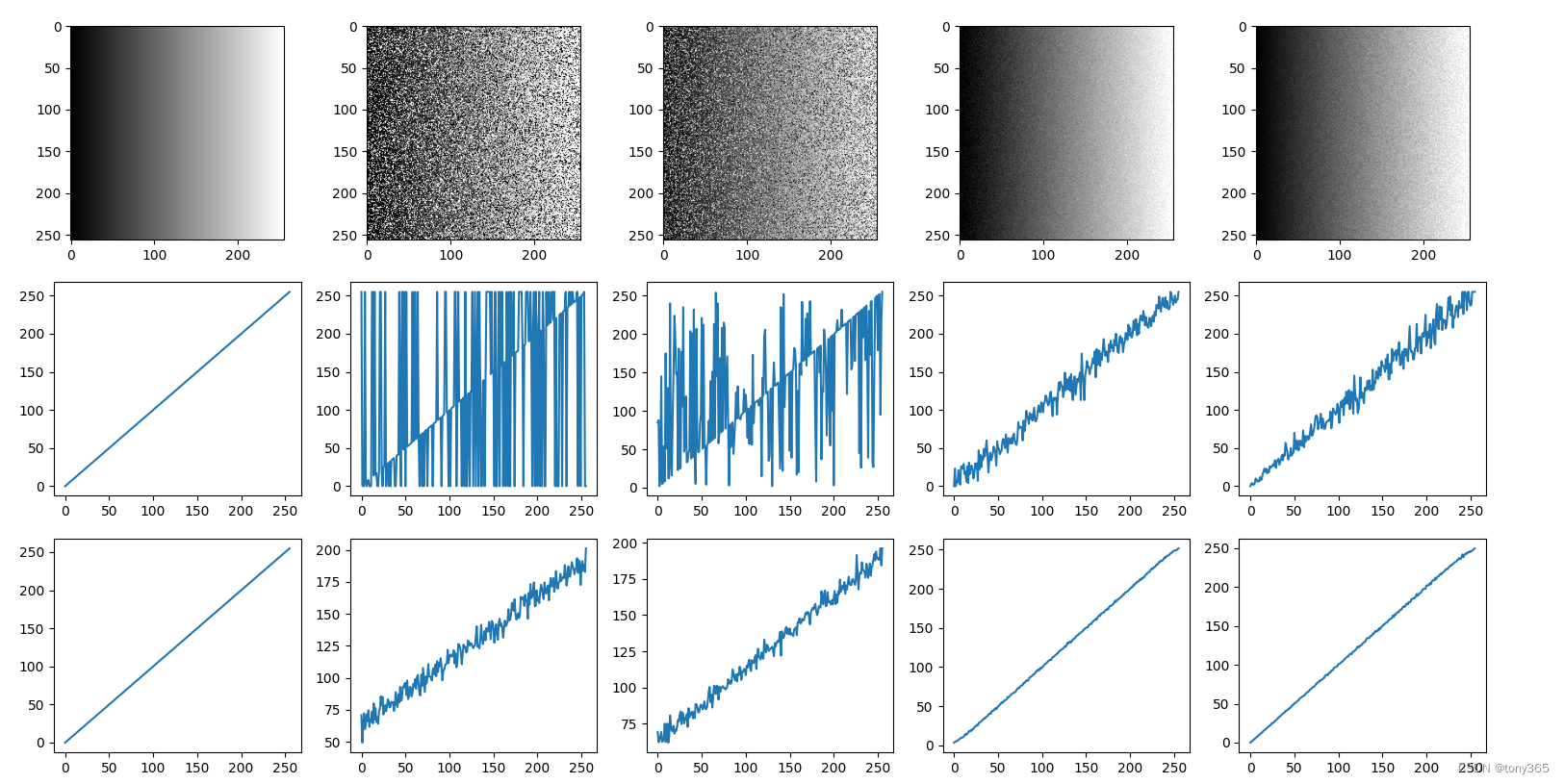
如下图：

1. 第一行是原图像素值分别为0，1，2，3，4，5
2. 第二行apply possion噪声
3. 第三行使用异方差高斯近似表示possion噪声
4. 第四行固定方差的高斯噪声。

一般情况下 异方差高斯可以比较准确的表达泊松噪声，但是特别小的时候略有差异

3. 异方差高斯 噪声模型（泊松和高斯噪声混合）

论文 Practical Poissonian-Gaussian noise modeling and fitting for single-image raw-data. 和 sidd:A High-Quality Denoising Dataset for Smartphone Cameras

提到将__泊松和高斯噪声__一起建模为 异方差高斯模型：

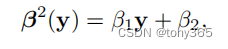
等式左边是方差， 右边y是无噪声图像值
beta1是与信号相关的 噪声参数，比如泊松噪声
beta2是与信号无关的 噪声参数，比如高斯噪声方差

怎么理解上面这个公式呢？
由于poisson分布可以近似为：

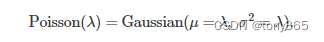
然后

$$\begin{gathered} P(lamda)+G(sigma) \\ =Gaussian(lamda,lamda)+Gaussian(0,sigm{a}^2) \\ =Gaussian(image,image)+Gaussian(0,sigm{a}^2) \\ =image+gaussian(0,image)+Gaussian(0,sigm{a}^2) \\ =image+Gaussian(0,beta1\ast image+beta2) \end{gathered}$$

所以：
beta1 = 1，beta2 = sigma^2， image是实际无噪声像素值。

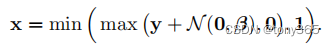
4. 几种噪声模型

如下图，分别是
原图， 椒盐噪声（50%的pixel被污染），随机噪声（50%的pixel被污染）， 高斯噪声和 泊松噪声

5. 信噪比 SNR的计算方法是

均值 / 标准差

https://www.23bei.com/tool/920.html

6. Practical Poissonian-Gaussian noise modeling and fitting for single-image raw-data

这篇文章首先是建立一个poisson-gaussian模型：
参考本文第二节。
这种近似通常是非常准确的。对于较小的光子计数，光子噪声通常由其他与信号无关的噪声源主导，对于较大的光子计数，中心极限定理确保泊松分布接近高斯分布.

然后对beta1和beta2参数进行估计：
估计方法肯定是通过 均值 和 方差来拟合直线。

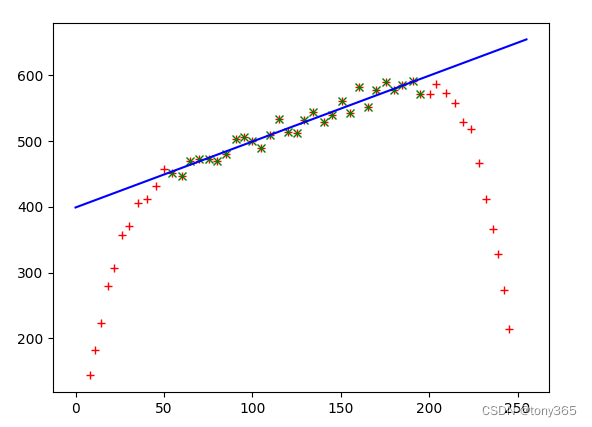
值为value = np.arange(0, 256, 5) 的若干个 patch(h=100pixel, w100pixel), 然后添加泊松噪声和高斯噪声。
计算出每块patch的均值作为 横坐标，
每块patch的方差作为纵坐标，
画出下图。
由于clip原因，在接近0和接近255的部分方差是不准确的（会下降），因此这里使用[50, 200]部分的点拟合直线，得到直线系数，即beta1, beta2。

https://blog.csdn.net/qq_34901691/article/details/119304917