线性可分和权重向量

单层感知机是后续深度学习的基础模型，本身没什么用，因为只能解决线性可分问题。

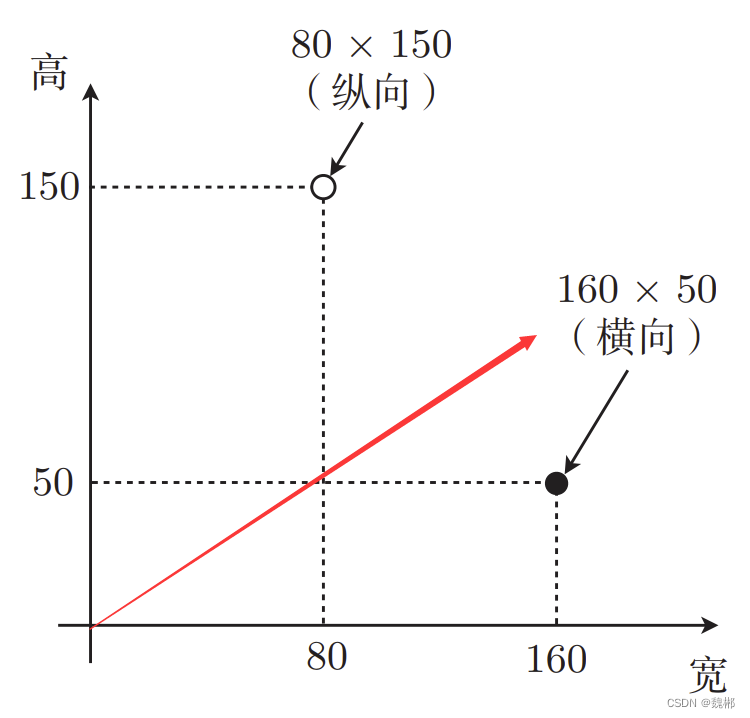
如这张图，想识别照片是横向的还是竖向的，只需要在中间画一条线，白点这个坐标就是纵向，黑点这个坐标就是横向，那么如何求呢。
首先，把这两个点的坐标看为向量

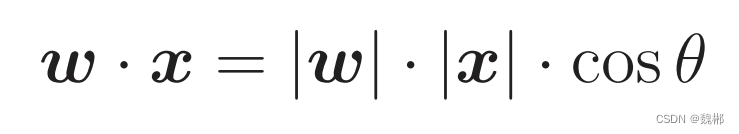
w是权重向量，线性可分那条线就是权重向量成为法线向量 所垂直的那条直线，通过这条直线可以区分训练数据

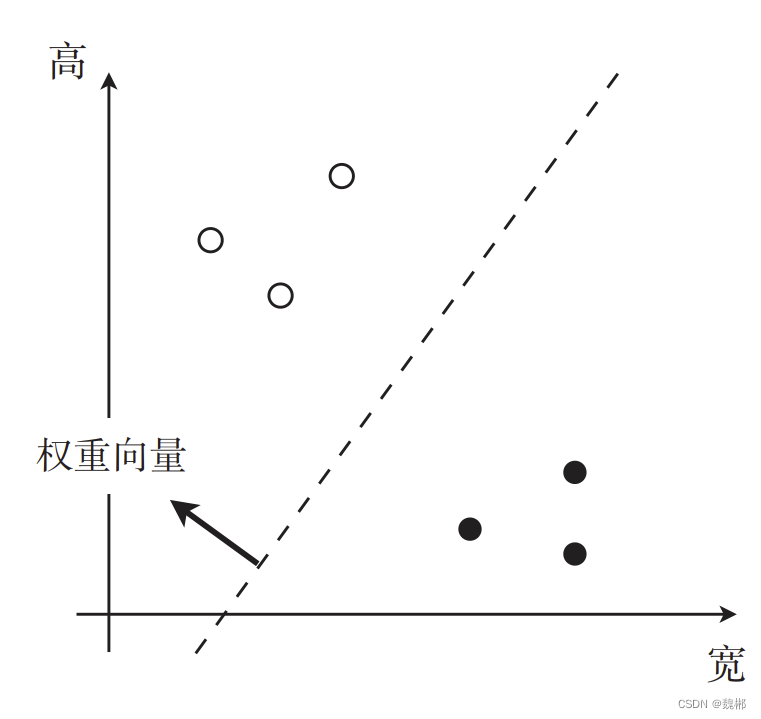
x就是所谓的训练数据的横纵坐标组成的向量，这俩的长度是绝对值，肯定是正数，那么符号就看cosθ了，cos90度到270度为负数，其余大于或等于0。
那么看下图

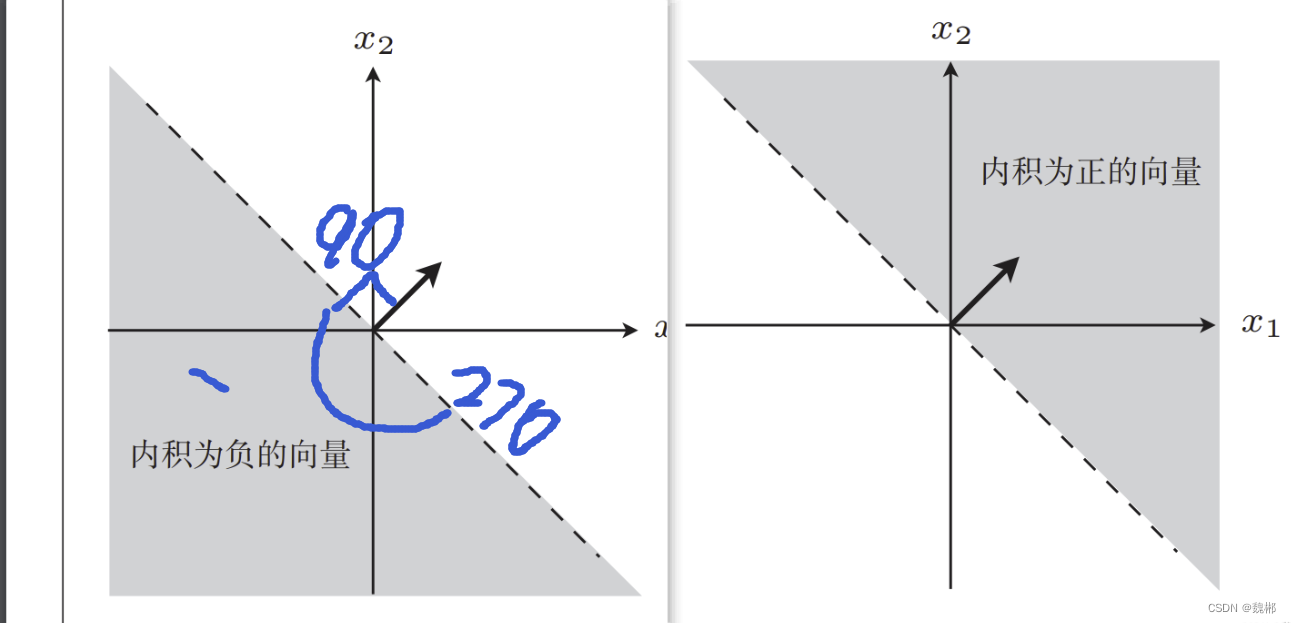
公式

判别函数
标签1为横。-1为纵

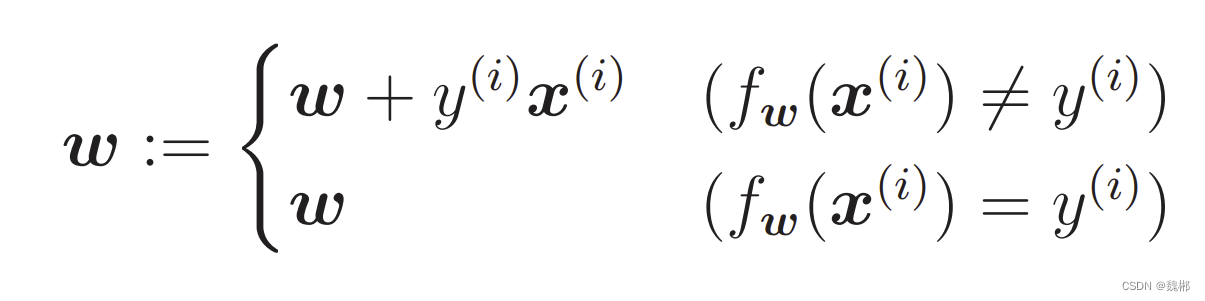
现在假设一有一条训练数据

然后随机生成一个权重向量，把他们都放在图上

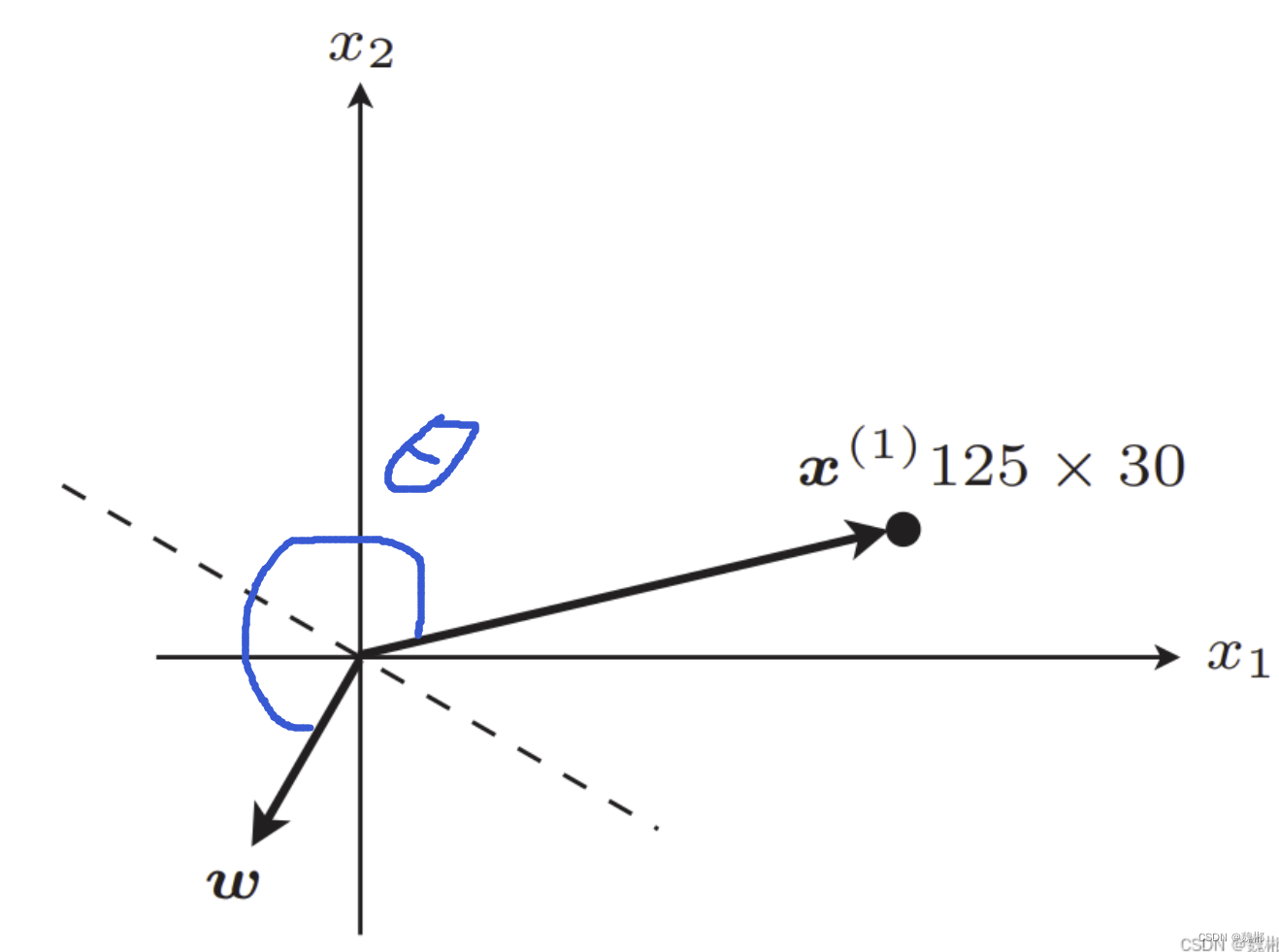
本条权重向量与该训练数据 的夹角 θ目测大约200来度，在90度到270度之间，那么cosθ的值为负，放到f（x1）里面，由cosθ决定符号，那么该函数的结果为负，打个标签-1.
f(x1) = -1. y1 = 1. 那么-1不等于1，就是f（x）不等于 y，执行判别函数满足条件的公式，即：
w：= w+y1*x1
w:= w+x1 (向量相加，就是把w的横纵坐标加上x的横纵坐标）
这构成了新的权重向量

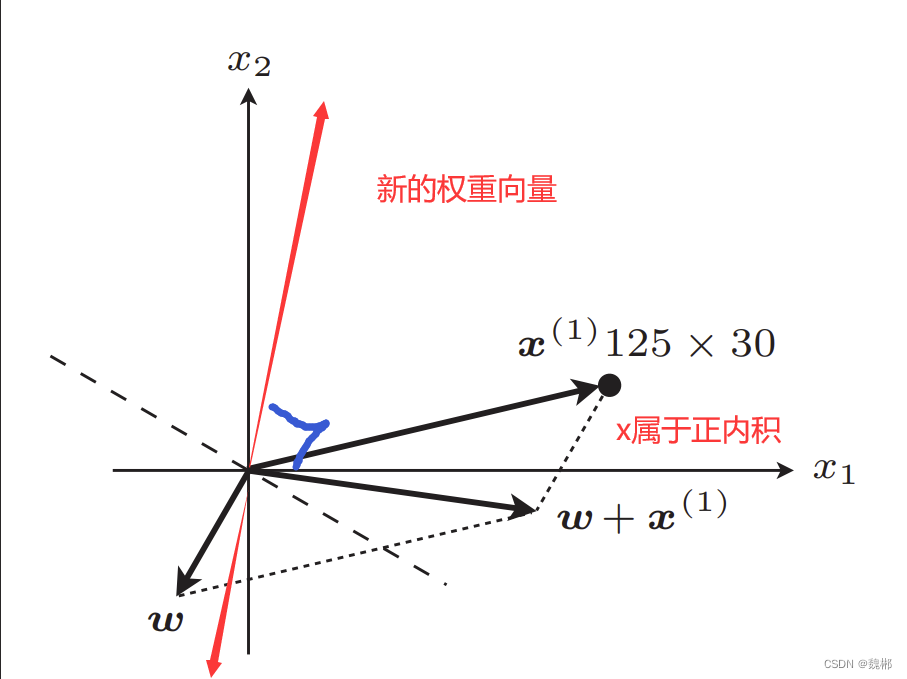
经过调整后的权重向量，对于本训练数据，判别结果与训练数据一致，如果我有多条训练数据，那么一条一条 训练，最终会找到一个权重向量 which 的直线可以 区分开数据。
这就是感知机

线性不可分

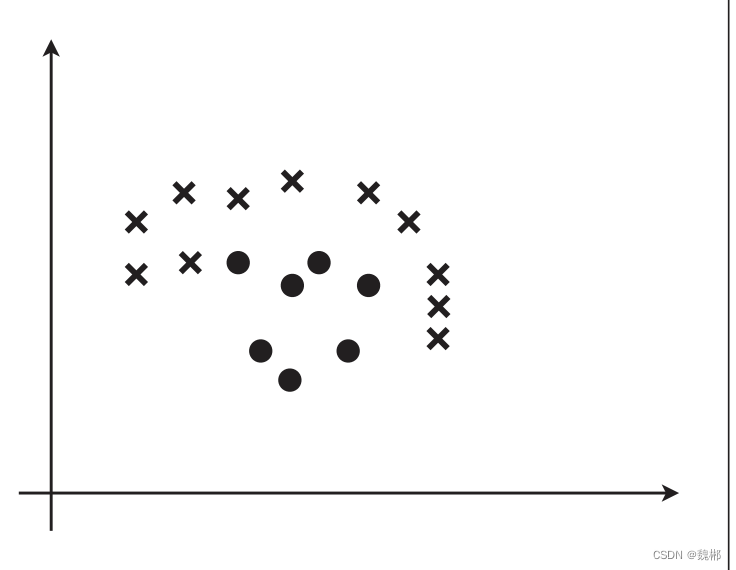
比如这玩意，一条线肯定分不出来，就需要更复杂的东西解决了