文章目录
- 快速排序
- 🔒题目
- 💡分析
- 🔑题解
快速排序
🔒题目
题目链接:785.快速排序-Acwing题库
💡分析
- 基本思想:
分治 - 主要步骤
- Step1:确定主元。从要划分的数组中选取一个元素作为主元,一般的选取方式有四种:①取最左边的元素 ②取最右边的元素 ③取中间的元素 ④随机选取(这四种选法根据个人喜好或者具体场景而定)
- Step2:划分区间。将数组中所有的元素于主元进行比较,直到使得左右区间能够恒大于等于或恒小于等于主元,如果我们想要升序排序,就可以让将所有小于等于主元的元素排在左边,所有大于主元的元素都在右边;如果我们想要降序排序,就可以将所有大于等于主元的元素都排在左边,所有小于主元的元素都在右边。当然这个等号左右两边任取其一即可,并不是非得让左边取等号
- Step3:递归进行Step1和Step2。我们通过Step1和Step2会划分出两个区间,然后再接着划分这两个区间,直到区间无法再进行划分(即区间只剩一个元素)时,此时数组就排序完毕了
🔑题解
时间复杂度: O ( n l o g n ) O(nlogn) O(nlogn)
- 方式一:每次选取区间中最右边的元素为主元,双指针从左往右遍历
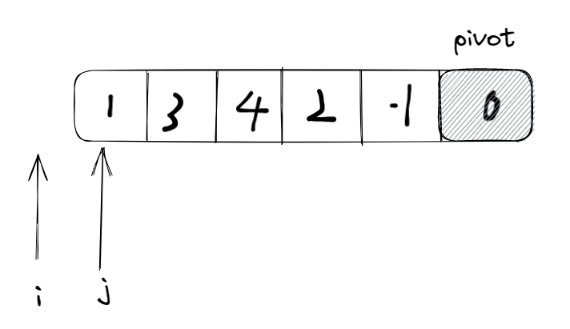
i负责标记左区间和右区间的分界点,而j负责遍历需要划分的区间,找出比主元小的元素,并将这个元素放到i+1的左侧,这样就能够实现区间的划分,最终使得i+1左侧的子区间恒小于pivot,i+1右侧的区间恒大于等于主元
import java.util.Scanner;
/**
* @author ghp
* @title 快速排序
* @description
*/
public class Main {
public static void main(String[] args) {
// 接收输入
Scanner sc = new Scanner(System.in);
int n = sc.nextInt();
int[] arr = new int[n];
for (int i = 0; i < arr.length; i++) {
arr[i] = sc.nextInt();
}
// 快速排序
quickSort(arr, 0, arr.length - 1);
// 输出结果
for (int i = 0; i < arr.length; i++) {
System.out.print(arr[i] + " ");
}
}
/**
* 快速排序
* @param arr 待排序的数组
* @param left 待划分区间的最左侧索引
* @param right 带划分区间的最右侧索引
*/
private static void quickSort(int[] arr, int left, int right) {
if (left >= right) {
// 区间中只有一个元素时,排序完毕,递归结束
return;
}
// 划分区间,并获取划分数组的主元索引,用于下一次的划分
int pivot = partition(arr, left, right);
quickSort(arr, left, pivot-1); // 继续划分左侧区间
quickSort(arr, pivot+1, right); // 继续划分右侧区间
}
/**
* 划分区间(增序排序)
* @param arr 待排序的数组
* @param left 待划分区间的最左侧索引
* @param right 带划分区间的最右侧索引
* @return 返回本次用于划分区间的主元
*/
private static int partition(int[] arr, int left, int right) {
// 选取主元
int pivot = arr[right];
int i = left-1;
int temp;
// 划分区间(左侧区间<主元,右侧区间>=主元)
for (int j = left; j < right; j++) {
if(arr[j] < pivot) {
// 将比主元小的元素放到(i+1)的左侧
temp = arr[j];
arr[j] = arr[i+1];
arr[i+1] = temp;
i++;
}
}
// 将主元放到分界点
temp = arr[right];
arr[right] = arr[i+1];
arr[i+1] = temp;
// 返回主元索引
return i+1;
}
}
-
方式二:每次选取区间最左边的元素为主元,指针双向遍历(左指针从左往右遍历,找比主元大的;右指针从右往左遍历,找比主元小的)
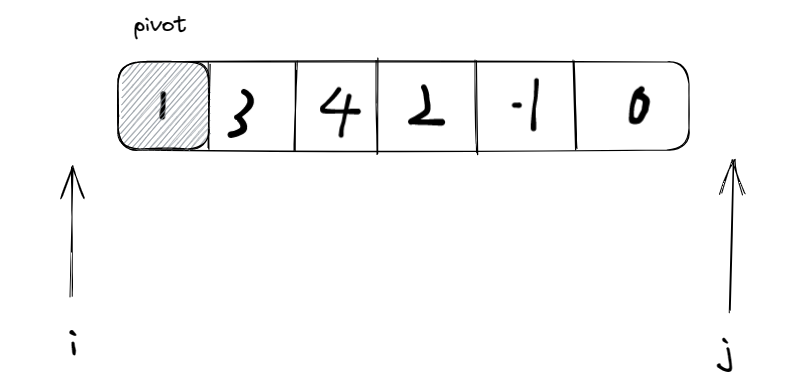
i从左到右遍历,找 >=pivot的元素,j从右往左遍历,找 <= pivot 的元素,然后交换i和j找的的元素,最终遍历完后,就会使得,左区间的元素都 <= pivot,右区间的元素都 >= pivotimport java.util.Scanner; /** * @author ghp * @title 快速排序 * @description */ public class Main { public static void main(String[] args) { // 接收输入 Scanner sc = new Scanner(System.in); int n = sc.nextInt(); int[] arr = new int[n]; for (int i = 0; i < arr.length; i++) { arr[i] = sc.nextInt(); } // 快速排序 quickSort(arr, 0, arr.length - 1); // 输出结果 for (int i = 0; i < arr.length; i++) { System.out.print(arr[i] + " "); } } /** * 快速排序 * * @param arr 待排序的数组 * @param left 待划分区间的最左侧索引 * @param right 带划分区间的最右侧索引 */ private static void quickSort(int[] arr, int left, int right) { if (left >= right) { // 区间中只有一个元素时,排序完毕,递归结束 return; } // 划分区间,并得到分界点的索引 int index = partition(arr, left, right); quickSort(arr, left, index-1); // 继续划分左侧区间 quickSort(arr, index, right); // 继续划分右侧区间 } /** * 划分区间 * @param arr 待排序的数组 * @param left 待划分区间的最左侧索引 * @param right 带划分区间的最右侧索引 * @return 返回分界点的索引 */ private static int partition(int[] arr, int left, int right) { // 选取主元 int pivot = arr[right]; int i = left - 1; int j = right + 1; // 划分区间(左侧区间<=主元,右侧区间>=主元) while (i < j) { // 从左往右遍历,寻找>=主元的元素 do { i++; } while (arr[i] < pivot); // 从右往左遍历,寻找<=主元的元素 do { j--; } while (arr[j] > pivot); // 判断区间是否划分完毕 if (i < j) { // 区间还未划分完毕,需要交换元素 int temp = arr[i]; arr[i] = arr[j]; arr[j] = temp; } } // 返回分界点 return i; } }方式二的效率是要高于方式一的,但是容易发生边界问题
注意事项:
-
情况1:返回的是
i-
如果
pivot取的是arr[left],则划分的区间是【left, index】和【index+1, right】 -
如果
pivot取的是arr[right],则划分的区间是【left, index-1】和【index, right】
记忆技巧:主元在左就+1,主元在右就-1
上面这两个必须配套使用,如果选错了就会出现递归死循环
如果
pivot取的是arr[left],但划分区间选择【left, index-1】和【index, right】,就会出现如下图所示的死循环: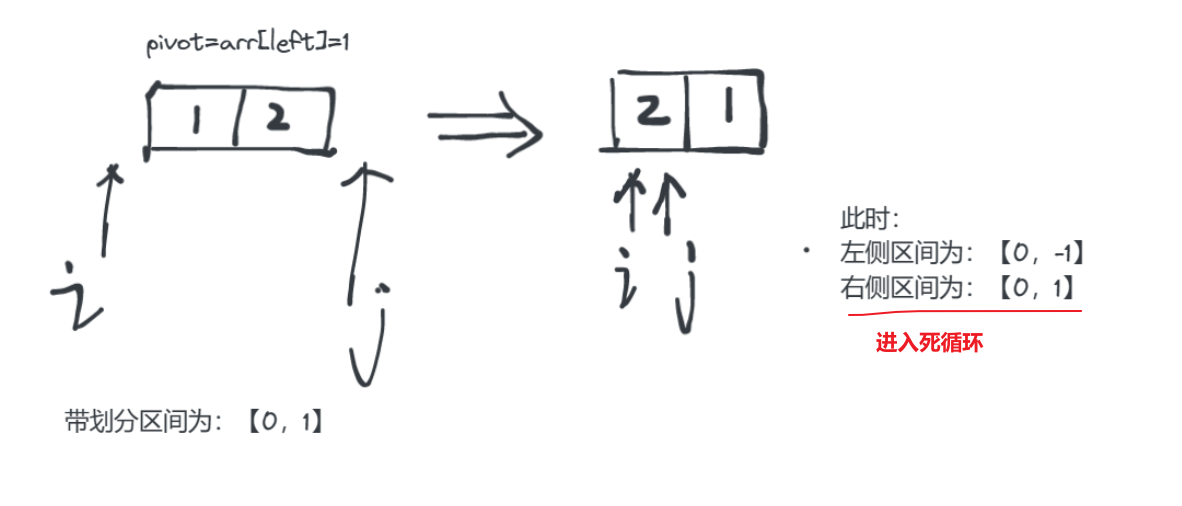
PS:其实也不需要死记硬背,当pivot取值 arr[left] 时,我们可以明确主元在左,而每次我们循环实用 if 寻找符合条件的元素时,此时我们的 i 索引对应的元素至少是和主元相等的,所以返回的 i 所划分的区间就是【left, i】和【i+1, right】。同理如果主元选择 arr[right] ,如果返回的是i,此时主元在右边,此时 i 索引对应的元素是可能比主元大的,因为每次遍历 if 寻找符合目标的元素,i都会自增,所以 i 划分的区间为【left, i-1】和【i,right】
-
-
情况2:返回的是
j- 如果
pivot取的是arr[left],则划分的区间是【left, j】和【j+1, right】 - 如果
pivot取的是arr[right],则划分的区间是【left,j-1】和【j, right】
推导思路和上面是一致的
- 如果
-