前言：

最近在做三维重建，尤其是Nerf方面多视角合成工作的时候，意识到了cuda的编程计算可以大大提高其中渲染的计算，最明显的例子是Instant-ngp，Plenoxels等文章，因此后面会学Cuda一段时间，同时也就开了这个新坑。
因为笔者也是cuda新手，所以大家有问题的话可以评论区指出，一起学习进步！

Nvidia Cuda官方入门资料

运行环境：

Windows10，Visual Studio2019,显卡3050Ti
（大家自行根据自己笔记本情况去配环境，或者没有gpu，租借云服务器去学习也是可以的）

1：C++模板

首先从下面的C++代码开始
其作用为把2个数组元素相加，代码里设为1<<20，也就是在二进制下把00001左移20位，最终值为2^20，为1048576，大约位1million（百万），相加的值最终减去3.0，判断有没有误差。

#include <iostream>
#include <math.h>

// function to add the elements of two arrays
void add(int n, float *x, float *y)
{
  for (int i = 0; i < n; i++)
      y[i] = x[i] + y[i];
}

int main(void)
{
  int N = 1<<20; // 1M elements

  float *x = new float[N];
  float *y = new float[N];

  // initialize x and y arrays on the host
  for (int i = 0; i < N; i++) {
    x[i] = 1.0f;
    y[i] = 2.0f;
  }

  // Run kernel on 1M elements on the CPU
  add(N, x, y);

  // Check for errors (all values should be 3.0f)
  float maxError = 0.0f;
  for (int i = 0; i < N; i++)
    maxError = fmax(maxError, fabs(y[i]-3.0f));
    //fabs（） 求浮点数的绝对值 fmax()返回2个参数最大的1个
  std::cout << "Max error: " << maxError << std::endl;

  // Free memory
  

输出如下

2：编写核函数cuda

（1）__global__可以理解为一个关键词，其告诉编译器该函数可以在GPU上运行，并且可以从CPU代码上调用
（2）这些__global__函数被称为内核，在GPU上运行的代码通常被称为device code，而在CPU上运行的代码被称为host code

// CUDA Kernel function to add the elements of two arrays on the GPU
__global__
void add(int n, float *x, float *y)
{
  for (int i = 0; i < n; i++)
      y[i] = x[i] + y[i];
}

3：Cuda下的内存分配（Memory Allocation）

（1）为了在GPU上进行计算，我需要分配GPU可访问的内存。CUDA中的统一内存通过提供系统中所有gpu和cpu可访问的单一内存空间使这一点变得容易。
（2）要在统一内存中分配数据，调用cudaMallocManaged()，它返回一个指针，您可以从host(CPU)code或device(GPU)code访问。要释放数据，只需将指针传递给cudaFree()。
（3）我只需要用对cudaMallocManaged()的调用替换上面代码中的new调用，并用对cudaFree（）来执行释放数值操作

  // Allocate Unified Memory -- accessible from CPU or GPU
  float *x, *y;
  cudaMallocManaged(&x, N*sizeof(float));
  cudaMallocManaged(&y, N*sizeof(float));
//理解为，分配空间指向 指针x指向的空间地址，大小为 N* x  x表示float的空间大小，因为有N个浮点数据，大约为1 million

  ...

  // Free memory
  cudaFree(x);
  cudaFree(y);

（4）在GPU上调用核函数需要在参数列表前添加符号<<< >>>
简单理解，启动1个GPU线程来运行add（）函数

add<<<1, 1>>>(N, x, y);

（5）目前为止，完整代码如下

#include <iostream>
#include <math.h>
// Kernel function to add the elements of two arrays
__global__
void add(int n, float *x, float *y)
{
  for (int i = 0; i < n; i++)
    y[i] = x[i] + y[i];
}

int main(void)
{
  int N = 1<<20;
  float *x, *y;

  // Allocate Unified Memory – accessible from CPU or GPU
  cudaMallocManaged(&x, N*sizeof(float));
  cudaMallocManaged(&y, N*sizeof(float));

  // initialize x and y arrays on the host
  for (int i = 0; i < N; i++) {
    x[i] = 1.0f;
    y[i] = 2.0f;
  }

  // Run kernel on 1M elements on the GPU
  add<<<1, 1>>>(N, x, y);

  // Wait for GPU to finish before accessing on host
  cudaDeviceSynchronize();

  // Check for errors (all values should be 3.0f)
  float maxError = 0.0f;
  for (int i = 0; i < N; i++)
    maxError = fmax(maxError, fabs(y[i]-3.0f));
  std::cout << "Max error: " << maxError << std::endl;

  // Free memory
  cudaFree(x);
  cudaFree(y);
  
  return 0;
}

这只是第一步，因为正如所写的那样，这个内核只适用于单个线程，因为运行它的每个线程都会对整个数组执行add操作。此外，由于多个并行线程会读取和写入相同的位置，因此存在竞争条件。

4：并行线程计算

（1）找出内核运行时间的最简单方法是使用nvprof来运行它，nvprof是CUDA工具包附带的命令行GPU分析器。
（2）上述代码我们体验了利用GPU上一个线程来进行计算。那如何并行呢！
下面代码表示CUDA运行时在GPU上启动要使用多少并行线程，这里选取256个线程

add<<<1, 256>>>(N, x, y);

（3）如果我在运行代码时只做了这样的修改，它将对每个线程执行一次计算，而不是将计算分散到并行线程上。为了正确地做到这一点，我需要修改内核，引入了两个量：
threadIdx.x：包含了the index of the thread within the block，块中的线程索引。此例中，index范围为0~255。
blockDim.x：包含了the size of thread block（number of threads in the thread block）线程块的大小，等于线程块中的线程数量。此例中，该值为256

__global__
void add(int n, float *x, float *y)
{
  int index = threadIdx.x;
  int stride = blockDim.x;
  for (int i = index; i < n; i += stride)
      y[i] = x[i] + y[i];
}

下面是运行结果（这里其实计算给出结果相较之前会更快）

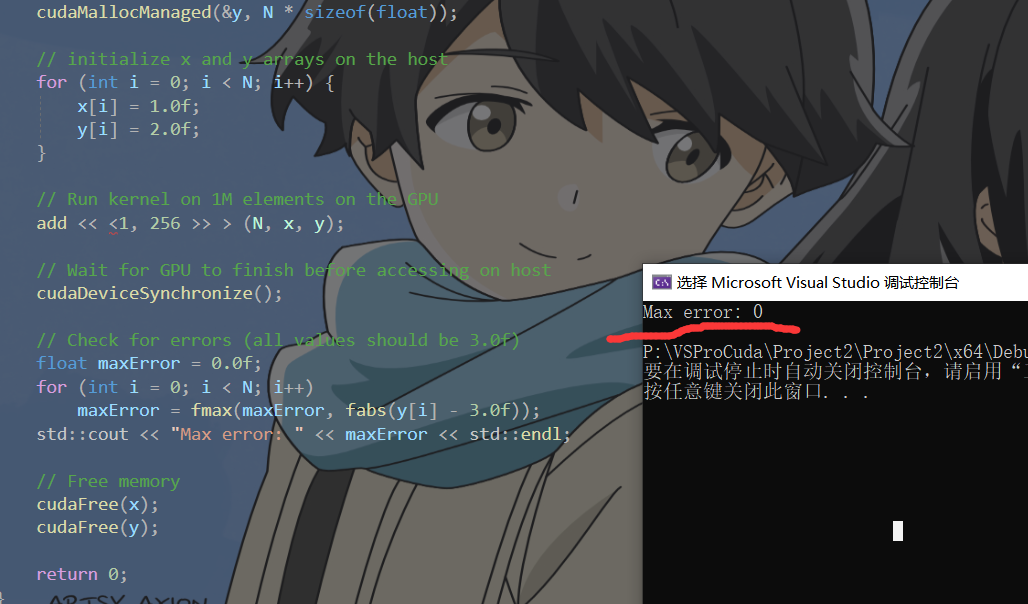
官网给出的比较：
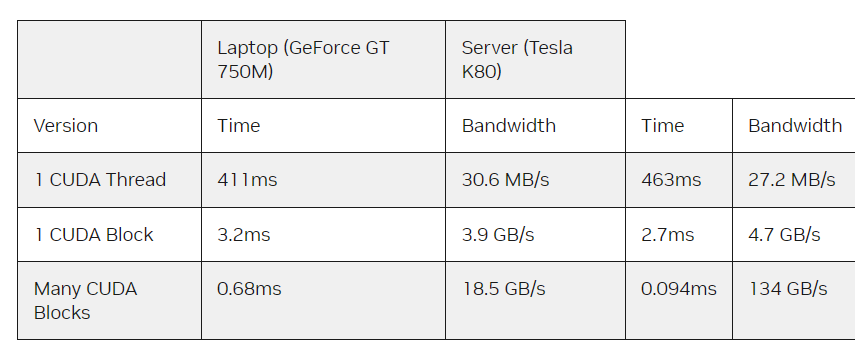
这是一个很大的加速(从463ms减少到2.7ms)。

5：Out of the Blocks

（1）CUDA gpu有许多并行处理器，它们被分组为流多处理器(SMs)。每个SM可以运行多个并发线程块。为了充分利用CUDA GPU，kernel应启动多个thread blocks。

（2）到目前为止，我们可以想到执行配置的第一个参数指定了线程块的数量。这些并行线程块一起构成了所谓的网格grid。因为我有N个元素要处理，每个块有256个线程，所以我只需要计算块的数量来获得至少N个线程。我只是用N除以块大小(注意，如果N不是blockSize的倍数，就要四舍五入)。

int blockSize = 256;//并行线程数量
//使用N 除以块大小，表示 线程块数量
int numBlocks = (N + blockSize - 1) / blockSize;
add<<<numBlocks, blockSize>>>(N, x, y);

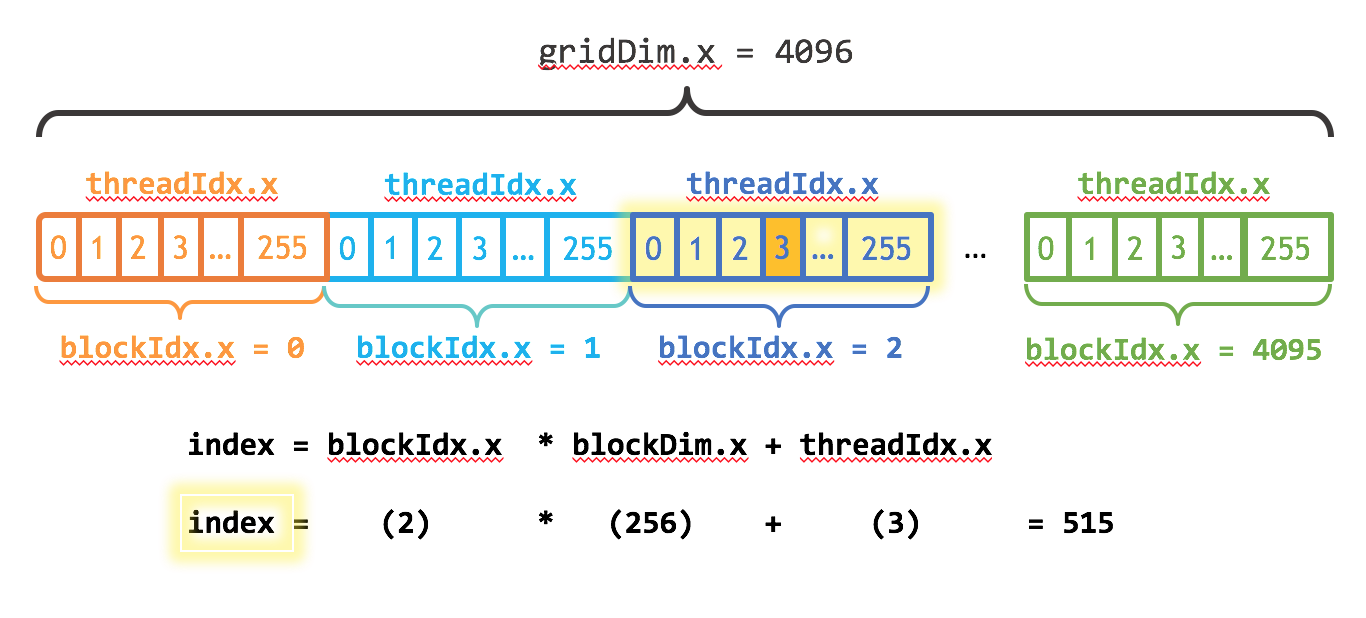
（3）我还需要更新内核代码，以考虑到线程块的整个网格。CUDA提供gridDim.x，其中包含网格中的块数量，以及blockIdx.x ,它包含网格中当前线程块的索引。
再引入两个量：
blockIdx.x：包含the index of the block with in the grid。网格中线程块的索引
gridDim.x：包含the size of the grid。网格大小，可以理解为网格中块的数量

图1说明了在CUDA中使用blockDim.x , gridDim.x 和 threadIdx.x对数组(一维)进行索引的方法。其思想是，每个线程通过计算其块开始的偏移量(块索引乘以块大小:blockIdx)来获得其索引。
这个想法是，每个线程通过计算其块开始的偏移量(块索引乘以块大小)来获得其索引:blockIdx.x* blockDim.x)。并在块中添加线程的索引threadIdx.x。

__global__
void add(int n, float *x, float *y)
{
  int index = blockIdx.x * blockDim.x + threadIdx.x;
  int stride = blockDim.x * gridDim.x;
  for (int i = index; i < n; i += stride)
    y[i] = x[i] + y[i];
}

更新后的kernel还将stride设置为网格中（blockDim.x*gridDim.x）的线程总数。在CUDA内核中，这种类型的循环通常被称为网格跨步循环。

最终代码如下

#include <iostream>
#include <math.h>
#include<stdint.h>
#include<cuda.h>
#include "cuda_runtime.h"
#include "device_launch_parameters.h"
#include <stdio.h>
// Kernel function to add the elements of two arrays
__global__
void add(int n, float* x, float* y)
{
    int index = blockIdx.x * blockDim.x + threadIdx.x;
    int stride = blockDim.x * gridDim.x;
    for (int i = index; i < n; i += stride)
        y[i] = x[i] + y[i];
}

int main(void)
{
    int N = 1 << 20;
    float* x, * y;

    // Allocate Unified Memory – accessible from CPU or GPU
    cudaMallocManaged(&x, N * sizeof(float));
    cudaMallocManaged(&y, N * sizeof(float));

    // initialize x and y arrays on the host
    for (int i = 0; i < N; i++) {
        x[i] = 1.0f;
        y[i] = 2.0f;
    }

    // Run kernel on 1M elements on the GPU
  //  add <<<1, 256 >>> (N, x, y);


    int blockSize = 256;//并行线程数量
//使用N 除以块大小，表示 线程块数量
    int numBlocks = (N + blockSize - 1) / blockSize;
    add << <numBlocks, blockSize >> > (N, x, y);



    // Wait for GPU to finish before accessing on host
    cudaDeviceSynchronize();

    // Check for errors (all values should be 3.0f)
    float maxError = 0.0f;
    for (int i = 0; i < N; i++)
        maxError = fmax(maxError, fabs(y[i] - 3.0f));
    std::cout << "Max error: " << maxError << std::endl;

    // Free memory
    cudaFree(x);
    cudaFree(y);

    return 0;
}

6：结果比较（性能）

额外知识补充

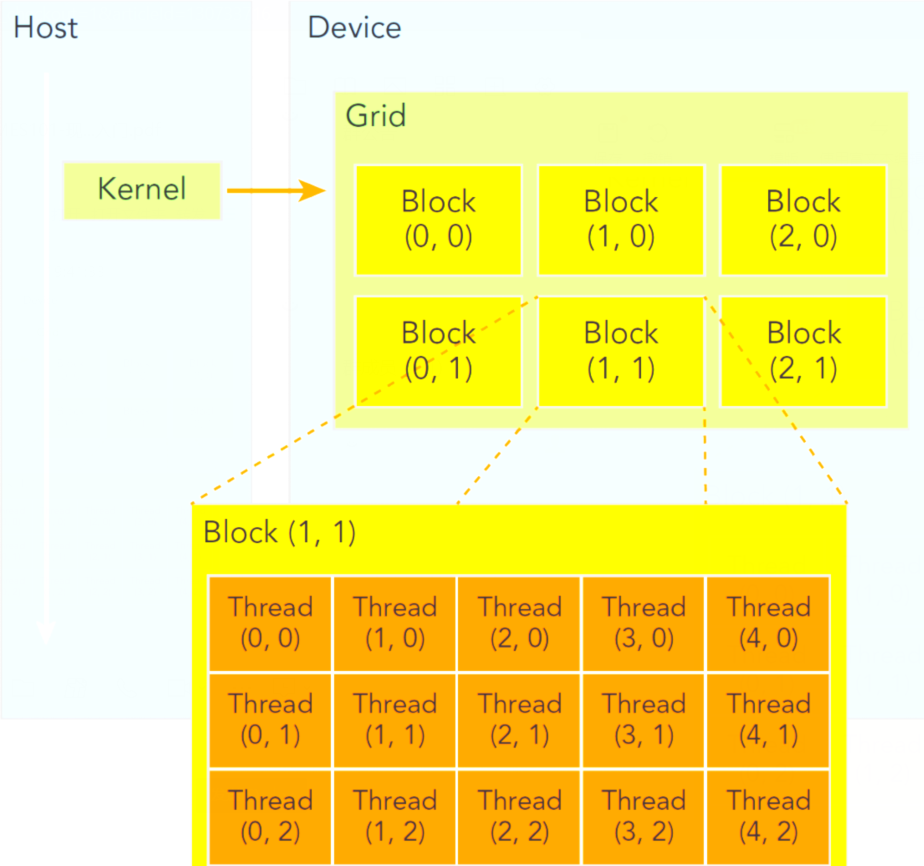
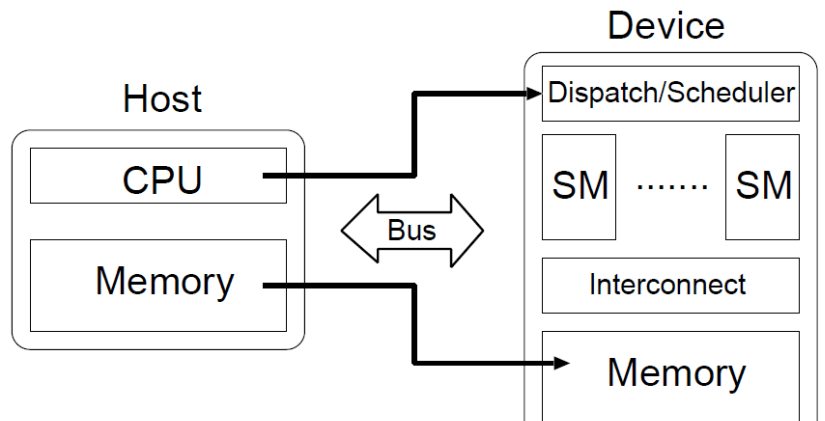
代码被分成两部分，一部分是在CPU上，也称之为在Host上，另一部分是在GPU上，也称之为在device上。他们两者的关系如下图所示

网格grids和线程块blocks

网格grids，在上层，至多可以分成三维的blocks，在不同block当中的线程是不能通信的；线程块blocks在相对较低的层级，同样可以将线程分成三维，而在同一个块中的线程是可以通信的。

对于一个核函数，只能有一个grid，但是可以有多个block，之所以将线程划分为grid和block是为了使得结构更清晰，便于线程管理，灵活运用。