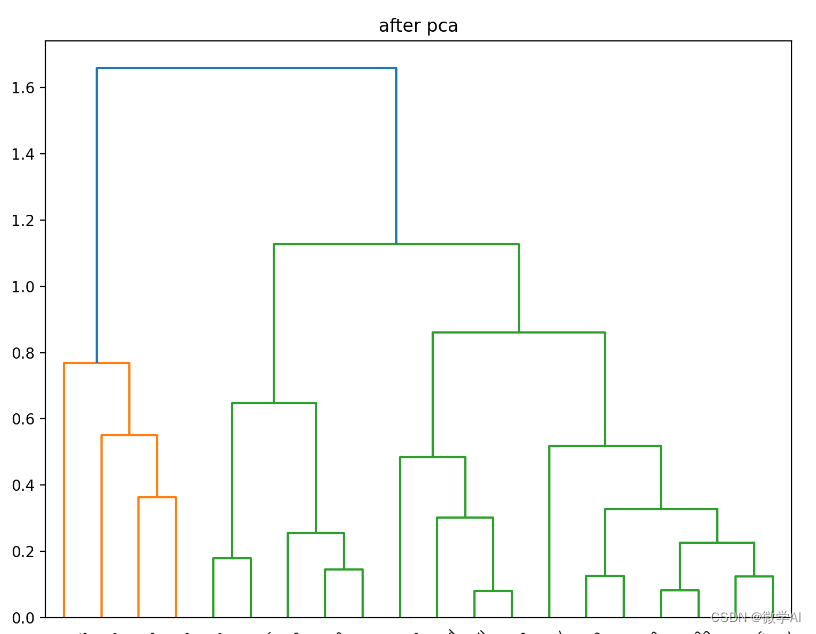
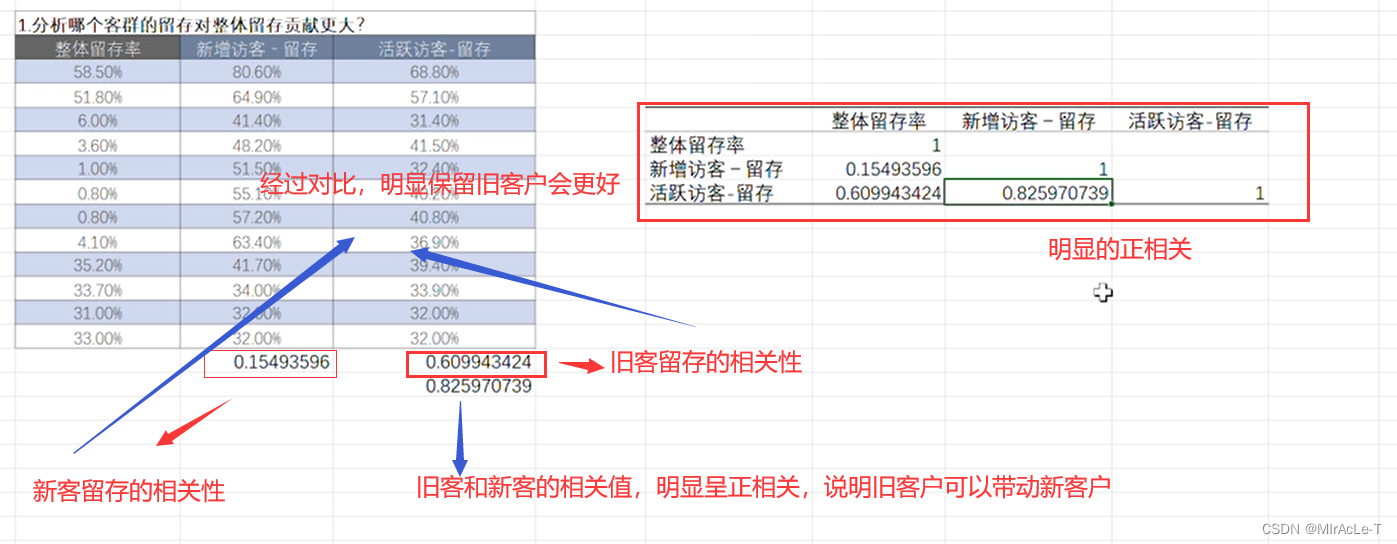
后续会有补充
并查集
查你在哪个集合,在有一定交集情况下会合并集合
可应用的场景:
1.分组
2.已有集合合并
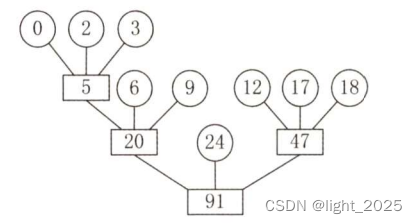
并查集就是把一组数据分组,把有共同特征的元素以树的形式放在一组

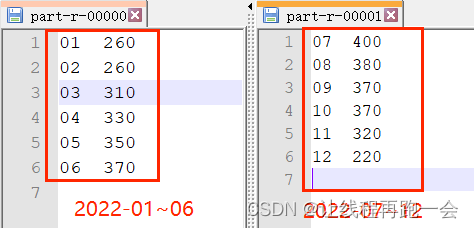
仔细观察数组中内融化,可以得出以下结论:
1. 数组的下标对应集合中元素的编号
2. 数组中如果为负数,负号代表根,数字代表该集合中元素个数
3. 数组中如果为非负数,代表该元素双亲在数组中的下标
图
图是由顶点集合及顶点间的关系组成的一种数据结构:G = (V, E)
其中:
顶点集合V = {x|x属于某个数据对象集}是有穷非空集合;
E = {(x,y)|x,y属于V}或者E = {<x, y>|x,y属于V && Path(x, y)}是顶点间关系的有穷集合,也叫做边的集合。
(x, y)表示x到y的一条双向通路,即(x, y)是无方向的;Path(x, y)表示从x到y的一条单向通路,即Path(x, y)是有方向的。
顶点和边:图中结点称为顶点,第i个顶点记作vi。两个顶点vi和vj相关联称作顶点vi和顶点vj之间有一条边, 图中的第k条边记作ek,ek = (vi,vj)或<vi,vj>。
有向图和无向图:在有向图中,顶点对<x, y>是有序的,顶点对<x,y>称为顶点x到顶点y的一条边(弧),<x, y>和<y, x>是两条不同的边,比如下图G3和G4为有向图。在无向图中,顶点对(x, y)是无序的,顶点对(x,y)称为顶点x和顶点y相关联的一条边,这条边没有特定方向,(x, y)和(y,x)是同一条边,比如下图G1和G2为无向图。注意:无向边(x, y)等于有向边<x, y>和<y, x>。
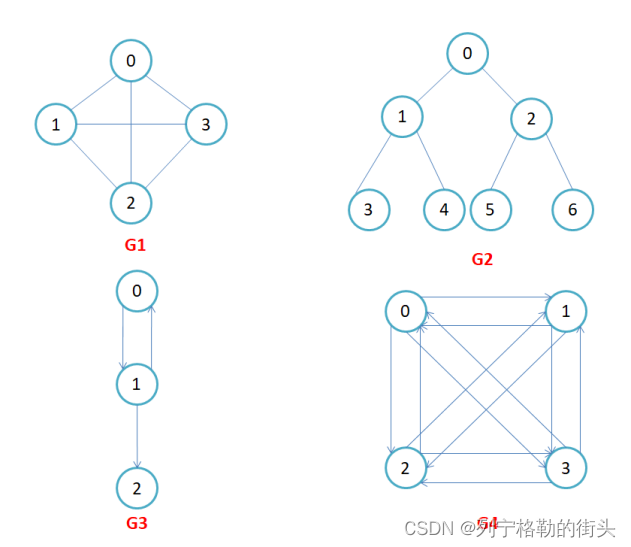
完全图:分为有向完全图和五项完全图。
邻接顶点:在无向图中G中,若(u, v)是E(G)中的一条边,则称u和v互为邻接顶点,并称边(u,v)依附于顶点u和v;在有向图G中,若<u, v>是E(G)中的一条边,则称顶点u邻接到v,顶点v邻接自顶点u,并称边<u, v>与顶点u和顶点v相关联。
顶点的度:顶点v的度是指与它相关联的边的条数,记作deg(v)。在有向图中,顶点的度等于该顶点的入度与出度之和,其中顶点v的入度是以v为终点的有向边的条数,记作indev(v);顶点v的出度是以v为起始点的有向边的条数,记作outdev(v)。因此:dev(v) = indev(v) + outdev(v)。注意:对于无向图,顶点的度等于该顶点的入度和出度,即dev(v) = indev(v) = outdev(v)。
路径:在图G = (V, E)中,若从顶点vi出发有一组边使其可到达顶点vj,则称顶点vi到顶点vj的顶点序列为从顶点vi到顶点vj的路径。
路径长度:对于不带权的图,一条路径的路径长度是指该路径上的边的条数;对于带权的图,一条路径的路径长度是指该路径上各个边权值的总和。

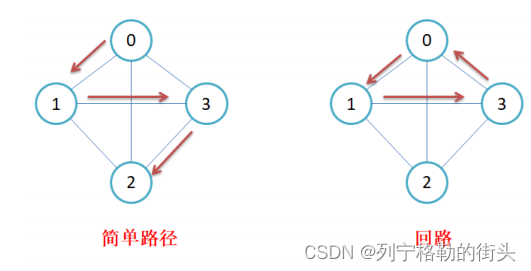
简单路径与回路:若路径上各顶点v1,v2,v3,…,vm均不重复,则称这样的路径为简单路径。若路径上第一个顶点v1和最后一个顶点vm重合,则称这样的路径为回路或环。
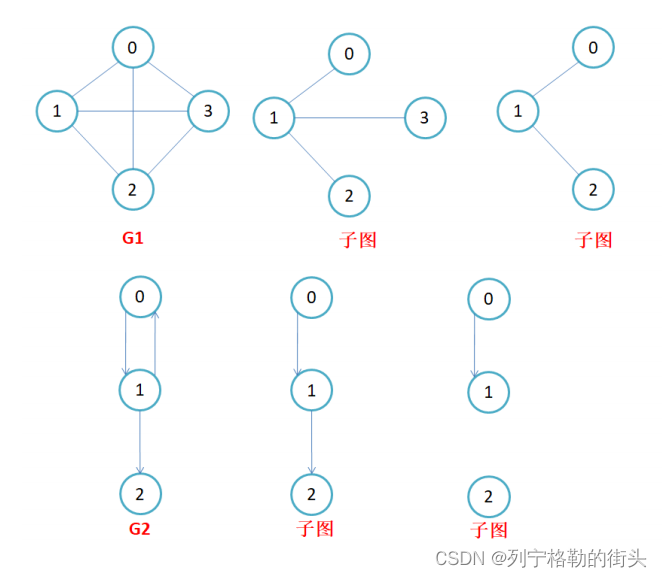
子图:设图G = {V, E}和图G1 = {V1,E1},若V1属于V且E1属于E,则称G1是G的子图。
连通图:在无向图中,若从顶点v1到顶点v2有路径,则称顶点v1与顶点v2是连通的。如果图中任意一 对顶点都是连通的,则称此图为连通图。
强连通图:在有向图中,若在每一对顶点vi和vj之间都存在一条从vi到vj的路径,也存在一条从vj到 vi的路径,则称此图是强连通图。
生成树:一个连通图的最小连通子图称作该图的生成树。有n个顶点的连通图的生成树有n个顶点和n- 1条边。
图的存储结构
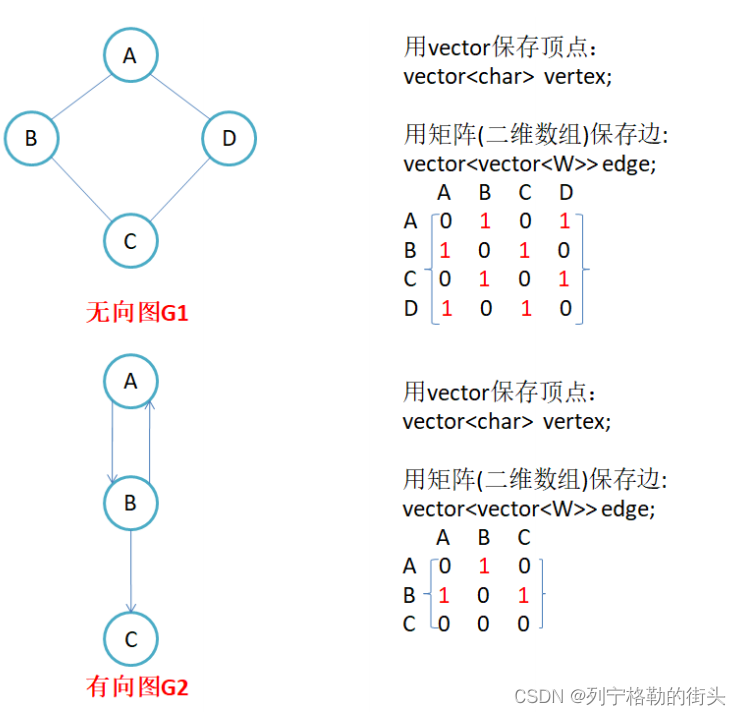
邻接矩阵
因为节点与节点之间的关系就是连通与否,即为0或者1,因此邻接矩阵(二维数组)即是:先用一个数组将定点保存,然后采用矩阵来表示节点与节点之间的关系。
注意:
1. 无向图的邻接矩阵是对称的,第i行(列)元素之和,就是顶点i的度。有向图的邻接矩阵则不一定是对称的,第i行(列)元素之后就是顶点i 的出(入)度。
2. 如果边带有权值,并且两个节点之间是连通的,上图中的边的关系就用权值代替,如果两个顶点不通,则使用无穷大代替
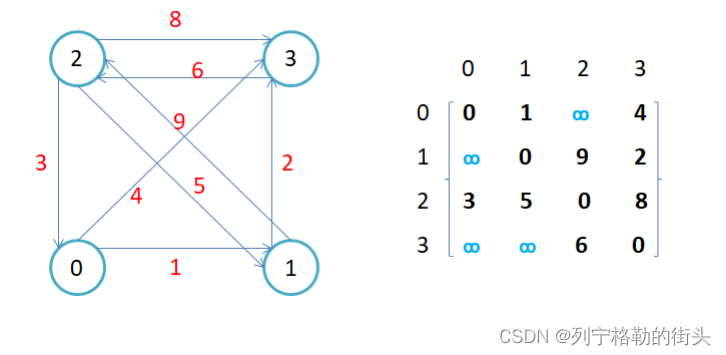
3. 用邻接矩阵存储图的有点是能够快速知道两个顶点是否连通,缺陷是如果顶点比较多,边比较少时,矩阵中存储了大量的0成为系数矩阵,比较浪费空间,并且要求两个节点之间的路径不是很好求。
邻接表
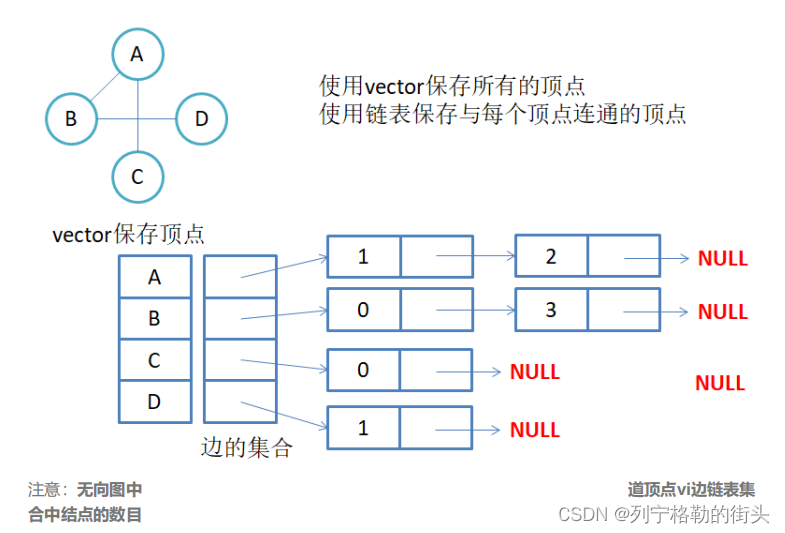
邻接表:使用数组表示顶点的集合,使用链表表示边的关系。
1.无向图邻接表存储
2.有向图邻接表存
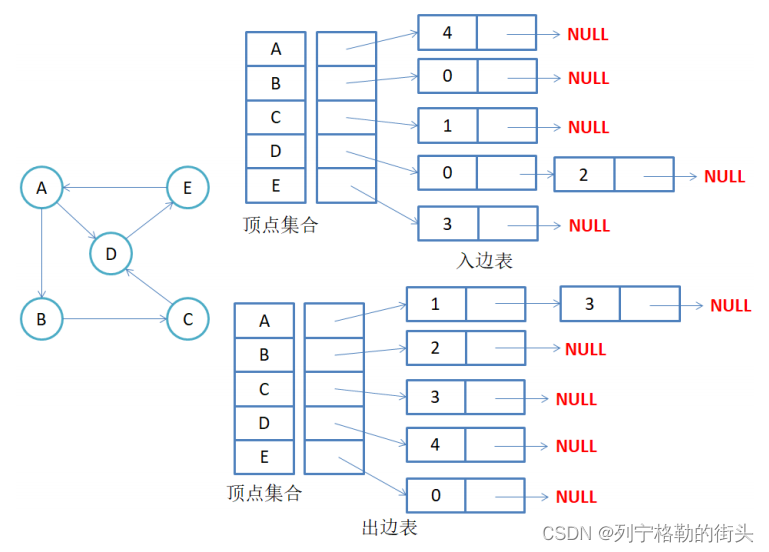
注意:有向图中每条边在邻接表中只出现一次,与顶点vi对应的邻接表所含结点的个数,就是该顶点的出度,也称出度表,要得到vi顶点的入度,必须检测其他所有顶点对应的边链表,看有多少边顶点的dst取值是i。

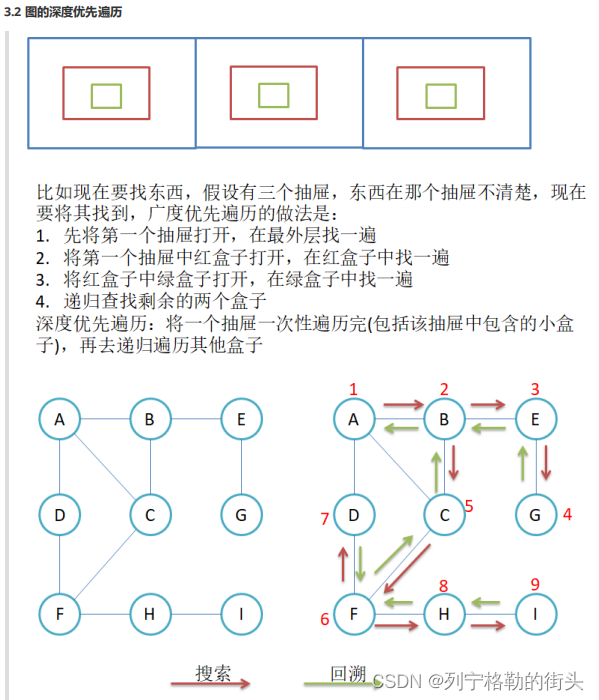
4. 最小生成树
连通图中的每一棵生成树,都是原图的一个极大无环子图,即:从其中删去任何一条边,生成树 就不在连
通;反之,在其中引入任何一条新边,都会形成一条回路。
若连通图由n个顶点组成,则其生成树必含n个顶点和n-1条边。因此构造最小生成树的准则有三 条:
1. 只能使用图中的边来构造最小生成树
2. 只能使用恰好n-1条边来连接图中的n个顶点
3. 选用的n-1条边不能构成回路
构造最小生成树的方法:Kruskal算法和Prim算法。这两个算法都采用了逐步求解的贪心策略。
贪心算法:是指在问题求解时,总是做出当前看起来最好的选择。也就是说贪心算法做出的不是整体 最优的
的选择,而是某种意义上的局部最优解。贪心算法不是对所有的问题都能得到整体最优解。