1. 基础的一些数据结构

（1）数组

用于存储一组具有相同类型的元素，将相邻的元素存储在连续的内存位置中，这使得数组的访问和操作更加高效。数组的长度在创建时就确定，并且不能动态改变。需要存储更多元素时，必须创建一个新的数组。数组的元素通过下标来访问，下标从0开始，表示元素在数组中的位置。可以使用下标快速访问和修改数组中的元素。

（2）链表

链表链表是一种数据结构，由一系列节点组成，每个节点包含数据和指向下一个节点的指针。

非连续存储：链表中的节点可以在内存中的任何位置存储，它们通过指针相互连接，形成链式结构。

动态长度：链表的长度可以动态改变，可以在任何时候添加或删除节点，不受固定长度的限制。

通过指针访问：要访问链表中的元素，需要从头节点开始，通过指针依次访问每个节点，直到达到目标节点。

不需要连续空间：由于节点可以在内存中的任意位置存储，链表不需要连续的内存空间，可以更灵活地利用可用的内存。

插入和删除效率高：由于链表的动态性，插入和删除节点的操作相对高效。只需改变节点之间的指针连接，不需要像数组那样移动其他元素。

随机访问效率低：链表中的节点没有索引，无法像数组那样通过下标进行快速随机访问。必须从头节点开始遍历链表，直到达到目标位置。

额外的指针开销：链表中每个节点都需要一个指针来指向下一个节点，这会增加一定的额外内存开销。

可变的节点结构：链表的节点可以包含除数据之外的其他字段，如指向前一个节点的指针（双向链表）、标志位等，这使得链表可以支持更多的功能和操作。

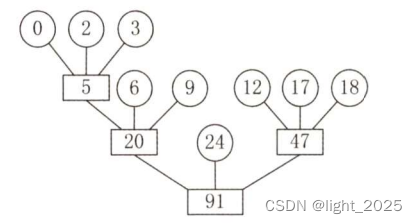
（3）二叉树

二叉树（Binary Tree）是一种树状数据结构，其中每个节点最多有两个子节点：左子节点和右子节点。二叉树具有以下特点：

节点度数：每个节点最多有两个子节点，因此节点的度数（子节点的数量）不超过2。

有序性：二叉树中的子节点有顺序之分，通常将左子节点视为左边的节点，右子节点视为右边的节点。

结构简单：相比于其他树结构，二叉树的结构相对简单，易于理解和实现。
深度和高度：二叉树的深度指的是从根节点到最远叶子节点的层数，而高度指的是从最底层叶子节点到根节点的层数。树的深度和高度可以相等，也可以不相等。

空节点：二叉树中的某些节点可以是空节点（null或空指针），表示没有子节点的情况。

遍历方式：二叉树可以通过不同的遍历方式来访问其中的节点，包括前序遍历、中序遍历和后序遍历等。

二叉搜索树：二叉树中的一种特殊形式是二叉搜索树（Binary Search Tree），它满足左子节点的值小于父节点的值，右子节点的值大于父节点的值，因此可以用于高效的查找、插入和删除操作。

平衡性：二叉树的平衡性指的是左右子树的高度差不超过一个常数，例如平衡二叉树（AVL树）和红黑树等。

总结来说，二叉树是一种有序的树状数据结构，每个节点最多有两个子节点。它具有简单的结构，可以通过不同的遍历方式进行节点访问。二叉搜索树是二叉树的一种特殊形式，具有高效的查找、插入和删除操作。平衡二叉树保持左右子树的平衡性，提供更快的操作性能。

（4）哈希表

哈希表（Hash table）是一种数据结构，通过使用哈希函数将键映射到存储位置来实现高效的插入、查找和删除操作。哈希表具有以下特点：

高效的查找操作：哈希表利用哈希函数将键转换为存储位置（索引），从而实现常数时间复杂度（O(1)）的查找操作。通过哈希函数，可以直接计算出键对应的存储位置，无需遍历整个数据集。

哈希函数映射：哈希函数将键映射到哈希表的存储位置。理想情况下，哈希函数能够将键均匀地映射到不同的存储位置，以最大程度地避免哈希冲突。

冲突处理：由于不同的键可能映射到相同的存储位置，哈希表需要处理冲突。常见的冲突解决方法包括链表法（使用链表存储冲突的键值对）和开放地址法（在发生冲突时寻找下一个可用的存储位置）等。

快速插入和删除操作：哈希表支持常数时间复杂度的插入和删除操作，因为通过哈希函数计算出存储位置后，可以直接访问到相应的位置并进行操作。

空间效率：哈希表的空间效率取决于数据集的填充因子（load factor），即存储的键值对数量与哈希表大小的比率。较低的填充因子可以减少冲突的概率，提高空间效率。

无序性：哈希表中的键值对通常是无序存储的，没有固定的顺序。如果需要有序性，可以使用其他数据结构或辅助数据结构。

可变长度：哈希表的长度（存储位置的数量）通常是可变的，可以根据需要进行动态调整，以适应数据集的大小变化。

总结来说，哈希表是一种高效的数据结构，具有快速的查找、插入和删除操作。它利用哈希函数将键映射到存储位置，解决了键值对的存储和查找问题。冲突处理和合理的填充因子可以影响哈希表的性能和空间效率。哈希表适用于需要快速查找和插入操作的场景，如缓存、索引和字典等。

2. 有哪些常见的算法思想？

以下是一些常见的算法思想：

贪心算法（Greedy Algorithm）：在每个阶段选择当前看起来最好的选项，不进行回溯，以期望最终获得全局最优解。

分治算法（Divide and Conquer）：将问题划分为更小的子问题，解决子问题并将结果合并，逐步解决原始问题。

动态规划（Dynamic Programming）：将复杂问题分解为重叠的子问题，并使用记忆化技术或者构建状态表来避免重复计算，从而降低时间复杂度。

回溯算法（Backtracking）：通过递归的方式尝试所有可能的解，并在搜索过程中剪枝，回退到上一个状态，以找到满足条件的解。

分支限界算法（Branch and Bound）：通过剪枝策略和优先级队列，对搜索空间进行限制，减少搜索的范围，以找到最优解。

模拟退火算法（Simulated Annealing）：受到冶金学中退火的过程启发，通过随机搜索和接受差解的策略，以概率性地跳出局部最优解，寻找全局最优解。

遗传算法（Genetic Algorithm）：受到生物进化的启发，使用遗传操作（选择、交叉和变异）来模拟进化过程，以找到问题的最优解。

深度优先搜索（Depth-First Search，DFS）：通过深度优先的方式遍历图或树的所有节点，递归或使用栈来实现。

广度优先搜索（Breadth-First Search，BFS）：通过广度优先的方式遍历图或树的所有节点，使用队列来实现。

二分查找（Binary Search）：对于有序数组或有序列表，通过比较中间元素与目标元素的大小关系，将搜索范围缩小一半，以快速定位目标元素。

3. 常见排序算法及其复杂度

插入排序（Insertion Sort）：将未排序的元素逐个插入到已排序部分的合适位置，直到整个序列有序。

选择排序（Selection Sort）：每次从未排序的部分选择最小（或最大）的元素，放到已排序部分的末尾，直到整个序列有序。

堆排序（Heap Sort）：将序列构建成一个最大堆（或最小堆），然后将堆顶元素与最后一个元素交换并移除，重新调整堆，重复此过程直到整个序列有序。

希尔排序（Shell Sort）：将序列按照一定间隔分组，对每个分组进行插入排序，然后逐渐缩小间隔，重复插入排序操作，直到间隔为1，完成最后一次插入排序。

桶排序（Bucket Sort）：将元素根据值的范围划分为多个桶，然后将元素放入对应的桶中，再对每个桶中的元素进行排序，最后按照桶的顺序依次取出元素。

冒泡排序（Bubble Sort）：重复地比较相邻的两个元素，如果顺序不对则交换，直到整个序列有序。

快速排序（Quick Sort）：通过选择一个基准元素，将序列分割为两个子序列，其中一个子序列的元素均小于基准元素，另一个子序列的元素均大于基准元素，然后对子序列进行递归排序。

归并排序（Merge Sort）：将序列递归地分成两个子序列，分别对子序列进行排序，然后将两个有序子序列合并为一个有序序列。

基数排序（Radix Sort）：将元素按照位数进行排序，从最低位到最高位依次进行比较和排序，直到最高位，最终得到有序序列。