目录
- 1、案例要求
- 2、算法设计与实现
- 2.1 Prim算法
- 2.1.1 构造无向图
- 2.1.2 编写Prim算法函数
- 2.1.3 实现代码
- 2.1.4 运行结果截图
- 2.2 Kruskal算法
- 2.2.1 构造无向图
- 2.2.2 编写并查集UnionFind类
- 2.2.3 编写Kruskal算法
- 2.2.4 实现代码
- 2.2.5 运行结果截图
- 3、总结
1、案例要求
利用贪心算法思想,求无向图的最小生成树(分别完成Prim算法、Kruskal算法,其中,Kruskal算法要求使用并查集检查回路)
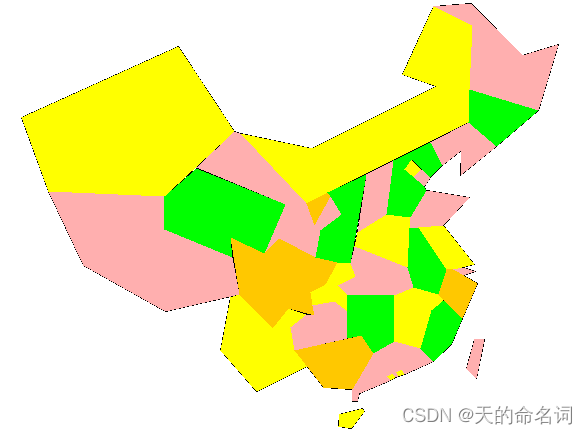
假设给定的无向图如下:
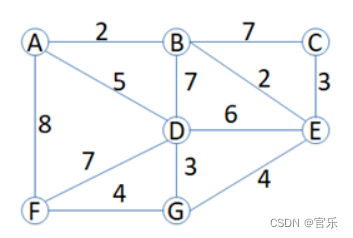
2、算法设计与实现
2.1 Prim算法
2.1.1 构造无向图
利用二维数组构造无向图,各路径设置为双向权值相同,不通的路径权值设置为最大整数。
2.1.2 编写Prim算法函数
lowcost数组记录当前最小生成树到其余点最短距离,初始状态为其他顶点到根节点的距离,mst记录记录其余顶点到最小生成树的边所经过顶点,初始化为1,遍历根节点以外的节点,找到距离二叉树最近且未在树中的顶点,将其加入,判断其余顶点从该新顶点到二叉树的距离是否更短,更短则更新lowcost数组和mst数组,直到所有顶点被遍历完。
2.1.3 实现代码
时间复杂度:O(n2)(n为顶点数)
public static int Prim(int[][] graph, int m) {
//设置两个数组
// lowcost:记录当前最小生成树到其余点最短距离
// mst:记录其余顶点到最小生成树的边所经过顶点,如mst[i]=j表示顶点i到最小生成树的边是i->j
int[] lowcost = new int[m + 1];
int[] mst = new int[m + 1];
//记录最小生成树的和
int sum = 0;
//数组初始化
for (int i = 2; i <= m; i++) {
//顶点1到其余顶点距离
lowcost[i] = graph[1][i];
//mst初始化为1
mst[i] = 1;
}
//第一个顶点已被遍历
mst[1] = 0;
//第二个点开始
for (int i = 2; i <= m; i++) {
int min = Integer.MAX_VALUE;
int minid = 0;
for (int j = 2; j <= m; j++) {
//找到距离二叉树最近的顶点且未在树中
if (lowcost[j] < min && mst[j] != 0) {
min = lowcost[j];
//记录顶点位置
minid = j;
}
}
//打印路径
System.out.println(mst[minid] + "->" + minid + " " + min);
sum += min;
lowcost[minid] = 0;
mst[minid] = 0;
for (int j = 2; j <= m; j++) {
//判断从新顶点到二叉树的距离是否更短
if (graph[minid][j] < lowcost[j]) {
//更新
lowcost[j] = graph[minid][j];
mst[j] = minid;
}
}
}
return sum;
}
2.1.4 运行结果截图
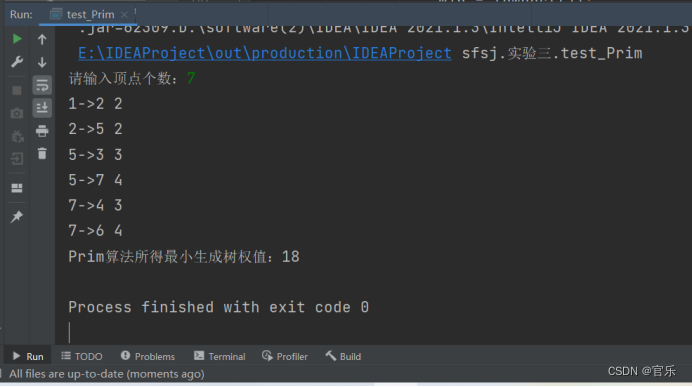
2.2 Kruskal算法
2.2.1 构造无向图
构造一个Edge类,有起点、终点、权值三个属性,重写compareTo函数,并用list列表存储无向图的各边。
2.2.2 编写并查集UnionFind类
union(x,y)函数实现合并功能,将节点x的父节点设置为节点y;find(x)函数实现查找功能,遍历查找x的父节点直到根节点,返回该根节点,为减少时间复杂度,同时记录查找过程的所有父节点,将所有节点的父节点设置为根节点,以便日后遍历查找耗费过多时间。
2.2.3 编写Kruskal算法
首先由边权值对边进行排序,从小到大,通过find(x)函数判断边上的两个点的根节点是否相同(判断加入后是否形成闭环),不同则加入最小生成树的边集中,同时通过union(x,y)对该边两顶点进行合并,最后直到最小生成树边集的边数==顶点数-1。
2.2.4 实现代码
时间复杂度:O(nlog2n)
并查集代码:
import java.util.HashSet;
import java.util.Set;
//并查集
public class UnionFind {
//实现查功能
public static UFNode find(UFNode x) {
UFNode p = x;
Set<UFNode> path = new HashSet<>();
//记录向上追溯的路径上的点
while (p.parent != null) {
path.add(p);
p = p.parent;
}
//这些点的parent全部指向这个集的代表(他们共同的老大)
//优化:第一次未生效,后续生效,后续只需找一次就能找到当前节点的根节点
for (UFNode ppp : path) {
ppp.parent = p;
}
return p;
}
//实现并功能
public static void union(UFNode x, UFNode y) {
//将x作为y的父结点
find(y).parent = find(x);
}
//定义静态内部类,这是并查集中的结点
public static class UFNode {
UFNode parent;//父结点
}
}
边类代码:
public class Edge<T> implements Comparable<Edge> {
private T start;
private T end;
private int distance;
public Edge(T start, T end, int distance) {
this.start = start;
this.end = end;
this.distance = distance;
}
public T getStart() {
return start;
}
public void setStart(T start) {
this.start = start;
}
public T getEnd() {
return end;
}
public void setEnd(T end) {
this.end = end;
}
public int getDistance() {
return distance;
}
public void setDistance(int distance) {
this.distance = distance;
}
@Override
public String toString() {
return start + "->" + end + " " + distance;
}
@Override
public int compareTo(Edge o) {
return distance > o.getDistance() ? 1 : (distance == o.getDistance() ? 0 : -1);
}
}
Kruskal算法代码:
public class Kruskal {
private final List<Edge> edgeList;//存放图中的所有边
private final int n;//总顶点数
private Set<Edge> T = new HashSet<>();//存放生成树的边
private Map pntAndNode = new HashMap();//边上的每个顶点都和并查集中有与之对应的node
private Set<Edge> getT() {
buildMST();
return T;
}
public Kruskal(List<Edge> edgeList, int n) {
this.edgeList = edgeList;
//为每个顶点建立一个并查集的点
for (Edge edge : edgeList) {
pntAndNode.put(edge.getStart(), new UnionFind.UFNode());
pntAndNode.put(edge.getEnd(), new UnionFind.UFNode());
}
this.n = n;
}
//构造一个边表
private static List<Edge> build() {
List<Edge> li = new ArrayList<>();
li.add(new Edge("1", "2", 2));
li.add(new Edge("1", "6", 8));
li.add(new Edge("1", "4", 5));
li.add(new Edge("2", "3", 7));
li.add(new Edge("2", "4", 7));
li.add(new Edge("2", "5", 2));
li.add(new Edge("3", "5", 3));
li.add(new Edge("4", "5", 6));
li.add(new Edge("4", "6", 7));
li.add(new Edge("4", "7", 3));
li.add(new Edge("5", "7", 4));
li.add(new Edge("6", "7", 4));
return li;
}
private void buildMST() {
//先对边集进行排序
Collections.sort(edgeList);
for (Edge e : edgeList) {
//寻找每条边上两个结点在map集合中映射的UFNode
UnionFind.UFNode x = (UnionFind.UFNode) pntAndNode.get(e.getStart());
UnionFind.UFNode y = (UnionFind.UFNode) pntAndNode.get(e.getEnd());
if (UnionFind.find(x) == UnionFind.find(y))
continue;//如果两个结点来自同一顶点集,则跳过这条边,否则会形成回路
UnionFind.union(x, y);
//把边加入到T中
T.add(e);
if (T.size() == n - 1)
return;//生成树的边数==总顶点数-1,表示所有的点已经连接
}
}
public static void main(String[] args) {
List<Edge> edgeList = build();
Kruskal obj = new Kruskal(edgeList, 7);
//getT中就调用了buildMST方法,将生成的边放到了集合中
for (Edge e : obj.getT())
System.out.println(e);
}
}
2.2.5 运行结果截图
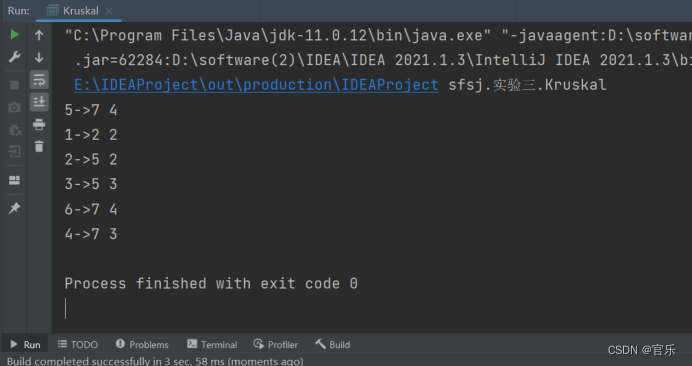
3、总结
贪心算法的基本思想:每次总选择最优情况,这次的prim算法是每次总选择距离最小生成树最近的边,kruskal算法是对边集进行排序后总选择最短边。
以及复习了并查集的相关知识,其中关键的两个函数union和find分别实现的合并功能与查找功能,在查找是还可以通过相关优化算法减少时间复杂度,如父节点更新法与加权标记法,在本案例中使用了父节点更新法。