brief

当研究两个有因果关系的变量时，我们希望建立一个方程式表示两者的关系，这样有一个变量得知时可以推测另一个变量。回归分析通常是一个好方法。
研究一因一果的回归分析称为一元回归分析，又分为直线回归和曲线回归。
研究多因一果的回归分析称为多元回归分析，又分为直线多元回归和多元曲线回归。
当然他还有很多变种：

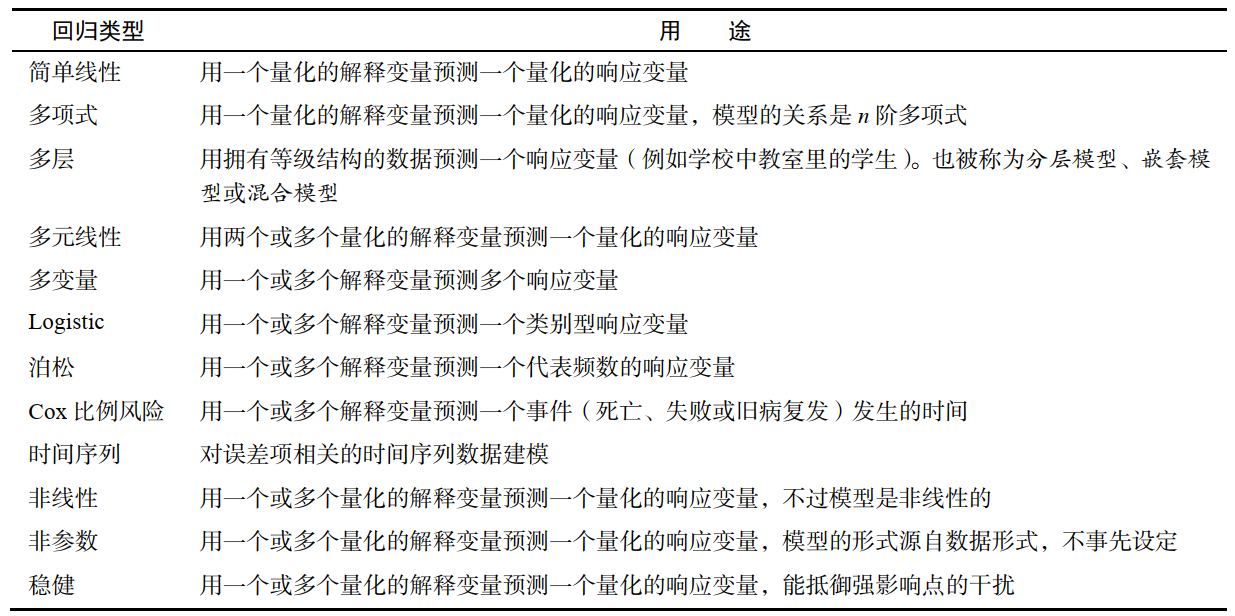
这里主要记录了一元直线回归分析的学习记录，包括前提假设，数学方程式，评价拟合有度，假设检验，模型应用。最后会把直线回归扩展到多元直线回归的应用上。

直线回归的一般形式

Y = a + bx

• Y 是响应变量的回归值
• x 是自变量的观测值
• a 是方程式的截距项，对应着x为0时Y的回归值
• b 称为回归系数，表示x变动一个单位Y相应的会变动几个单位

研究回归关系时，自变量x的每一个取值x_i 都有一个正态分布的y总体与之对应，而不是一个确定的y_i 与之对应。（或者说 当x = x_i 时，y_i 的平均数 Y 与之对应。 ）

参数计算

对于参数a，b一般 根据最小二乘法进行估算,最终使得 RSS = min( sum( (y_i - Y)²) ) 最小，
观测值y和回归值Y的残差平方和（ RSS）等于 sum( (y_i - Y)²)。

具体推导过程此处省略，推导结果如下：

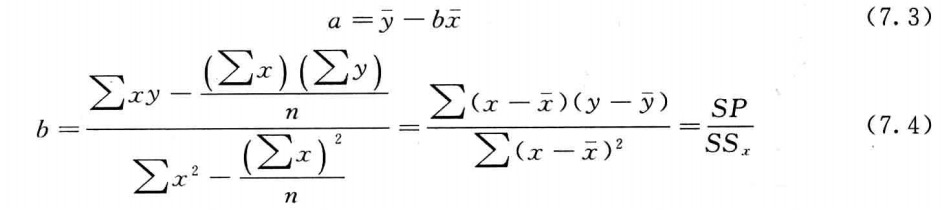
x的离均差与y的离均差乘积之和 sum[( x - mean(x)) (y - mean(y))] 记为SP
x的离均差的平方和sum[(x - mean(x))²] 记作 SS_x

y观测值和回归值的关系

基本前提假定

• 正态性：第一是指，对于固定的因变量x，都有一个正态总体Y与之对应；第二是指，观测值y包含有误差部分，误差是随机且正态分布的。
• 独立性：y的观测值相互独立
• 线性： 自变量和响应变量之间呈线性
• 同方差性：响应变量的方差不随自变量的水平变化而不同。
• 自变量x是没有误差的固定项，或者至少和观测y比起来，x的误差小到可以忽略不记。这一点在实际应用中常常被放宽。
• 如果是多元线性回归，自变量应该非共线性(不相关)

假设检验

直线回归的变异来源

观测值y是一个随机变量，y的总变异y - mean(y) 可以分解为两部分，第一部分是自变量x变异引起的变异 回归值Y - mean(y),第二部分是误差所引起的变异 y - Y。

所以观测值 y和回归值 Y的总变异可以写成：

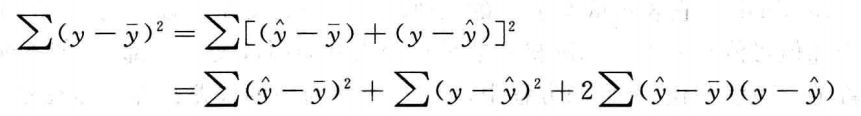
其中：

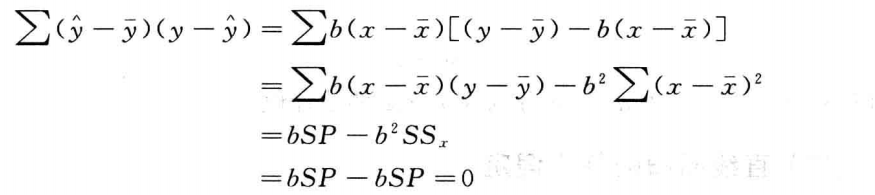
最终有：

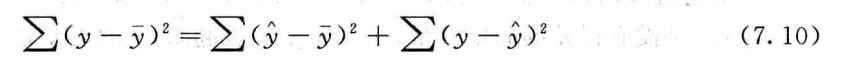
• 上式左边，sum[ (y - mean(y))² ] 为观测y的离均差平方和，表示随机变量y的总变异，记作SS_y。
• sum[ (Y - mean(y))² ] 为x变异引起的y变异的总平方和，称作回归平方和，记作SS_回归或者U。
• sum[ (y - Y)² ] 为误差引起的y变异的总平方和，称为残差平方和，记为SS_离回归或者Q。
• SS_回归越大说明回归效果越好，因为x可以解释y的变异。但是记住回归效果好不等于模型好。

自由度问题：

这里有待进一步探究，，我有点没想明白这个自由度的问题。

假设检验

• F检验
  参考单因素方差分析相关章节。
  这里我是这样理解的，U相当于X解释的方差部分，Q相当于误差能解释的方差部分，如果U和Q来自同一个正态总体，是不是说明U和Q没有显著差别，那也就是X能解释的方差和误差能解释的方差没有区别，所以线性方程Y = a + bx不是显著性能解释y的方程。

多元线性回归

多元也就是多个自变量x。

模型形式：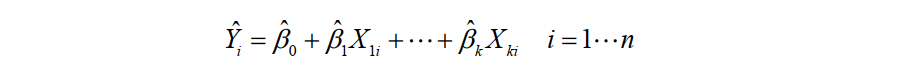

参数估计也是使得残差值的平方和 RSS = min( sum( (yi - Y)2) ) 最小估算而来。

前提假设以及方程的显著性检验和回归系数显著性的检验同上。