文章目录
- 谓词逻辑
- 辖域
- 变元的约束---换自由变元 不容易出错
- 枚举
- 前束范式
- 量词例子
- 练习题
- 特殊例子
- 如果明天下雨,则某些人将被淋湿
- 如果人都爱美,则漂亮的衣服有销路
- 谓词推理
- 量词相关规则 (去量词 加量词)
谓词逻辑

辖域

变元的约束—换自由变元 不容易出错

枚举


前束范式



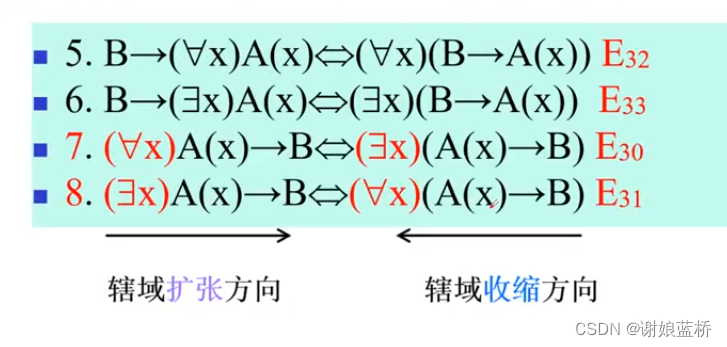



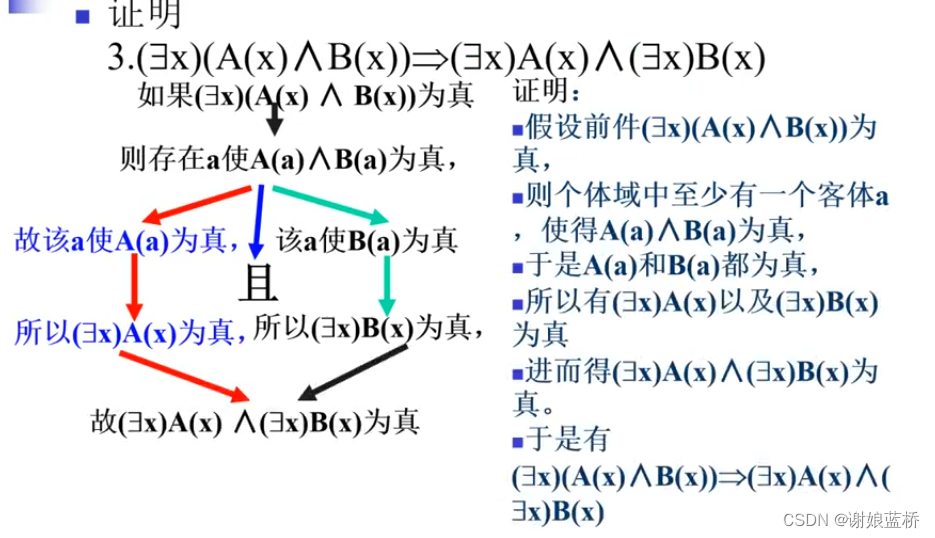
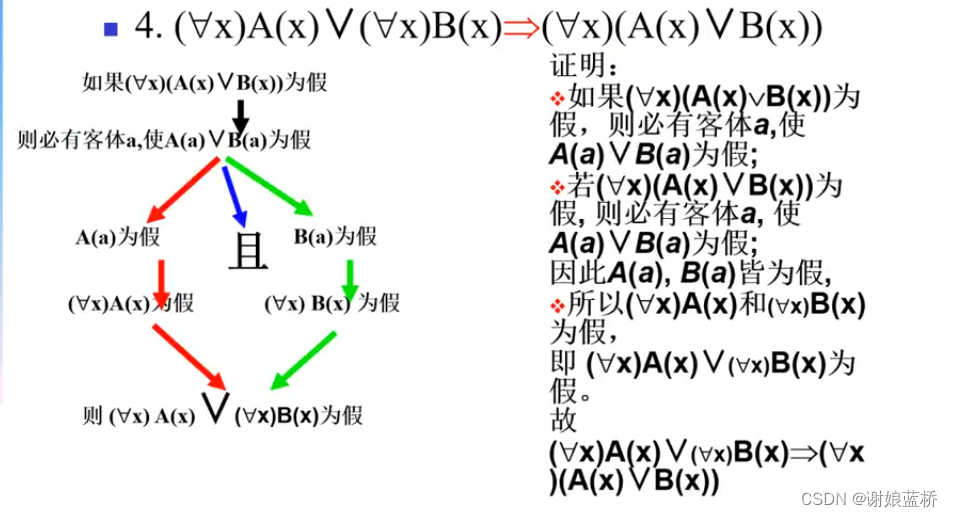
量词例子
全称量词
(
∀
x
)
条件前件加入
→
(\forall x) 条件前件加入 \to
(∀x)条件前件加入→
存在量词
(
∃
x
)
和取式
∧
(\exists x) 和取式 \wedge
(∃x)和取式∧
¬
∀
x
P
(
x
)
⟺
∃
x
¬
P
(
x
)
\neg\forall xP(x)\iff\exists x\neg P(x)
¬∀xP(x)⟺∃x¬P(x)
¬
∃
x
P
(
x
)
⟺
∀
x
¬
P
(
x
)
\neg\exists xP(x)\iff\forall x\neg P(x)
¬∃xP(x)⟺∀x¬P(x)
所有的老虎都要吃人
P
(
x
)
:
x
会吃人
U
(
x
)
:
x
是老虎
(
∀
x
)
(
U
(
x
)
→
P
(
x
)
)
P(x):x会吃人\\ U(x):x是老虎\\(\forall x)(U(x)\to P(x))
P(x):x会吃人U(x):x是老虎(∀x)(U(x)→P(x))
有些大学生吸烟
P
(
x
)
:
x
是大学生
U
(
x
)
:
x
吸烟
(
∃
x
)
(
P
(
x
)
∧
U
(
x
)
)
P(x):x是大学生\\ U(x):x吸烟\\(\exists x)(P(x)\wedge U(x))
P(x):x是大学生U(x):x吸烟(∃x)(P(x)∧U(x))
每个大学生都会说英语
P
(
x
)
:
x
是大学生
U
(
x
)
:
x
会说英语
(
∀
x
)
(
P
(
x
)
→
U
(
x
)
)
P(x):x是大学生\\U(x):x会说英语\\(\forall x)(P(x)\to U(x))
P(x):x是大学生U(x):x会说英语(∀x)(P(x)→U(x))
有一些自然数是素数
P
(
x
)
:
x
自然数
U
(
x
)
:
x
是素数
(
∃
x
)
(
P
(
x
)
∧
U
(
x
)
)
P(x):x自然数\\U(x):x是素数\\(\exists x)(P(x)\wedge U(x))
P(x):x自然数U(x):x是素数(∃x)(P(x)∧U(x))
所有大学生都喜欢一些歌星
S
(
x
)
:
x
是大学生
X
(
x
)
:
x
是歌星
L
(
x
,
y
)
:
x
喜欢
y
∀
x
(
S
(
x
)
→
∃
y
(
X
(
y
)
∧
L
(
x
,
y
)
)
S(x):x是大学生\\X(x):x是歌星\\L(x,y):x喜欢y\\\forall x(S(x)\to\exists y(X(y)\wedge L(x,y))
S(x):x是大学生X(x):x是歌星L(x,y):x喜欢y∀x(S(x)→∃y(X(y)∧L(x,y))
发光的不都是金子
P
(
x
)
:
x
是金子
Q
(
x
)
:
x
发光
¬
∀
x
(
P
(
x
)
→
Q
(
x
)
)
P(x):x是金子\\Q(x):x发光\\\neg\forall x(P(x)\to Q(x))
P(x):x是金子Q(x):x发光¬∀x(P(x)→Q(x))
某些人对食物敏感
P
(
x
)
:
x
是人
Q
(
x
)
:
x
是食物
F
(
x
,
y
)
:
x
对
y
过敏
∃
x
(
P
(
x
)
∧
∃
y
(
Q
(
y
)
∧
F
(
x
,
y
)
)
)
P(x):x是人\\Q(x):x是食物\\F(x,y):x对y过敏\\\exists x(P(x)\wedge\exists y(Q(y)\wedge F(x,y)))
P(x):x是人Q(x):x是食物F(x,y):x对y过敏∃x(P(x)∧∃y(Q(y)∧F(x,y)))
练习题

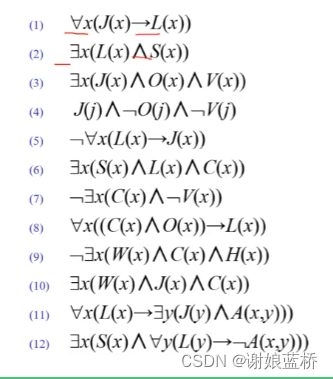
每个人都有些缺点
P
(
x
)
:
x
是人
Q
(
x
)
:
x
是缺点
F
(
x
,
y
)
:
x
有
y
∀
x
(
P
(
x
)
→
∃
y
(
Q
(
y
)
∧
F
(
x
,
y
)
)
)
P(x):x是人\\Q(x):x是缺点\\F(x,y):x有y\\\forall x(P(x)\to\exists y(Q(y)\wedge F(x,y)))
P(x):x是人Q(x):x是缺点F(x,y):x有y∀x(P(x)→∃y(Q(y)∧F(x,y)))
尽管有人聪明,但未必人人聪明
M
(
x
)
:
x
是人
,
S
(
x
)
:
x
聪明
∃
x
(
M
(
x
)
∧
S
(
x
)
)
∧
∀
x
(
M
(
x
)
→
S
(
x
)
)
M(x):x是人,S(x):x聪明\\\exists x(M(x)\wedge S(x))\wedge\forall x(M(x)\to S(x))
M(x):x是人,S(x):x聪明∃x(M(x)∧S(x))∧∀x(M(x)→S(x))
每个自然数有且仅有一个后继
特殊例子
如果明天下雨,则某些人将被淋湿
P : 明天下雨 ( 不是个体 ) , M ( x ) : x 是人 , W ( x ) : x 将被淋湿 P → ∃ x ( M ( x ) ∧ W ( x ) ) P:明天下雨 (不是个体),M(x):x是人,W(x):x将被淋湿\\P\to\exists x(M(x)\wedge W(x)) P:明天下雨(不是个体),M(x):x是人,W(x):x将被淋湿P→∃x(M(x)∧W(x))
如果人都爱美,则漂亮的衣服有销路
M ( x ) : x 是人, L ( x ) : x 爱美 C ( x ) : x 是衣服 B ( x ) : x 是漂亮的 S ( x ) : x 有销路 ∀ x ( M ( x ) → L ( x ) ) → ∀ y ( C ( y ) ∧ B ( y ) → S ( y ) ) M(x):x是人 ,L(x):x爱美 \\C(x):x是衣服 B(x):x是漂亮的\\S(x):x有销路\\ \forall x(M(x)\to L(x))\to\forall y(C(y)\wedge B(y)\to S(y) ) M(x):x是人,L(x):x爱美C(x):x是衣服B(x):x是漂亮的S(x):x有销路∀x(M(x)→L(x))→∀y(C(y)∧B(y)→S(y))
谓词推理

谓词推理—>命题推理 去量词
命题推理—>谓词推理 加量词
量词相关规则 (去量词 加量词)
先去存在量词 后去全称量词