半桥 LLC 谐振变换器主电路结构
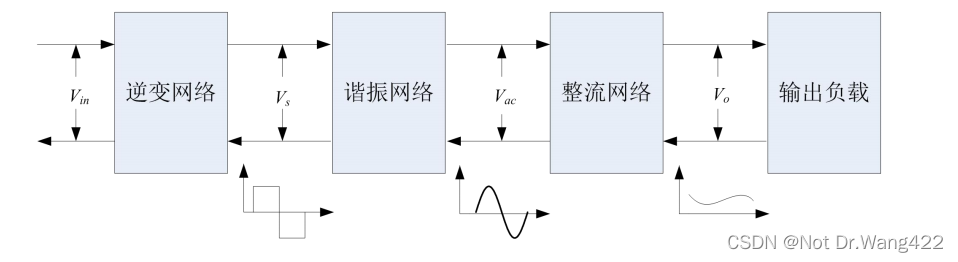
如图所示,半桥 LLC 谐振变换器主电路可以分为四个部分,即:逆变网络、谐振网络、变压器及整流滤波网络。两个 MOSFET(S1、S2)以及它们的体二极管(D1、D2)和寄生电容(C1、C2)构成了半桥逆变电路,谐振网络由三个谐振元件(励磁电感 Lm、谐振电感 Lr、谐振电容 Cr)组成。由于本课题方案副边整流滤波网络选用全波整流结构,所以变压器 T 副边绕组需要中心抽头,Cf为输出滤波电容。
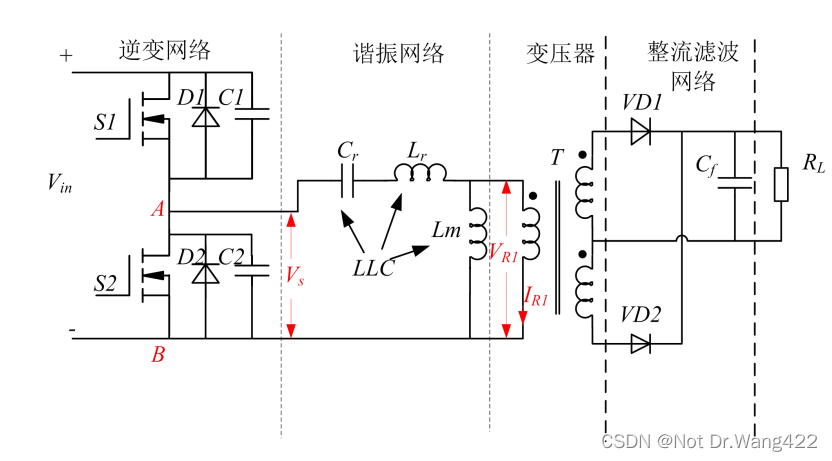
LLC 谐振变换器采用 PFM(脉冲频率调制),MOS 开关管 S1、S2 分别由两组PWM 驱动信号控制。两组驱动信号占空比接近 50%,为了防止半桥逆变电路上下桥臂直通,它们之间设有一定的死区时间,而死区时间的存在也是功率 MOS 管实现 ZVS 的前提条件。
LLC 谐振变换器实现 DC-DC 变换的过程如如图所示,由前级 EMI 和整流滤波电路转化而来的直流电压经过逆变网络被转换成频率可变的占空比为50%的方波,再经谐振网络和变压器 T 转换到副边,最终由整流滤波网络优化后以直流形式输出。
逆变拓扑电路的选择
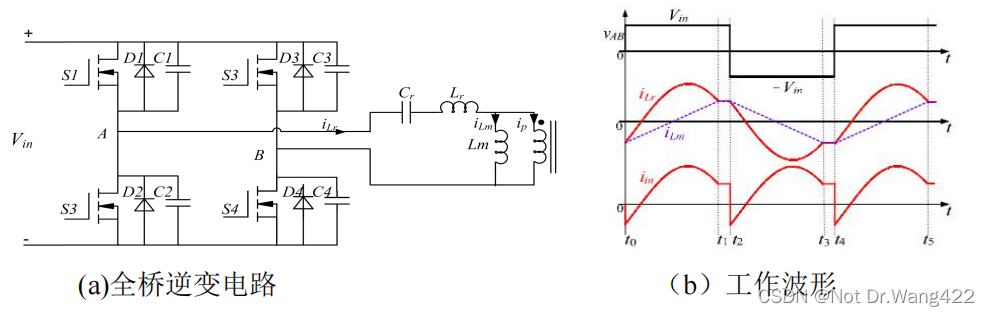
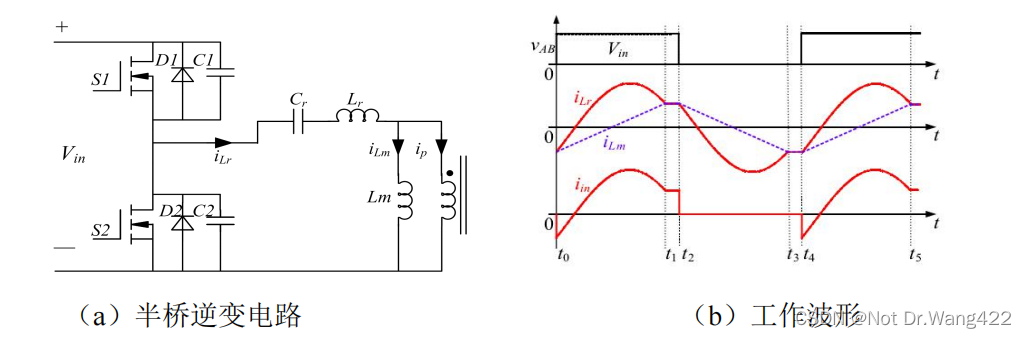
LLC 谐振变换器的逆变网络通常选用全桥逆变与半桥逆变这两种结构,它们的拓扑图和简单工作波形如上图所示。相较于半桥逆变器而言,全桥逆变器的开关电流应力减小了一半,对于开关管的要求略低,广泛用于大功率场合。而半桥逆变结构的优势在于电路结构简单,比全桥逆变电路少两个开关管,有利于样机设计和节约成本。
整流滤波电路的选择
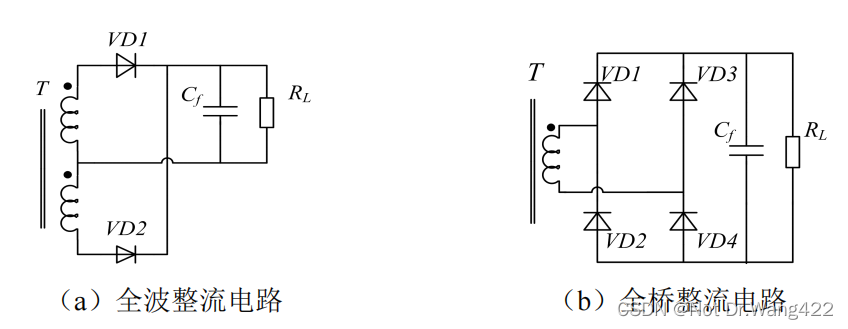
双端电路中常用的整流滤波电路形式有全波整流电路和全桥整流电路,其原理图如图所示。
由 LLC 谐振变换器的特性可知,谐振电感电流 ir 和励磁电感电流 im 之差折算到变压器副边,即为整流滤波网络输入电流。变换器逆变网络选择全桥整流电路时存在以下问题:由于电路中选用整流二极管数目较多,任意时刻变换器输出电流都要流经两个二极管,如果输出电流较大会造成很大的损耗。电路中每个整流二极管的电压应力等于变换器输出电压。
全波整流电路如图 (a)所示,电路中只选用两个整流二极管,变换器输出电
流只流经一个二极管,通态损耗较小。其缺点是:断态时,每个整流二极管的电压应力是两倍的输出电压,对整流二极管耐压要求高,并且变压器二次侧线圈有中心抽头,制造工艺相对复杂。
LLC 谐振变换器电路建模
基波分析法 FHA(First Harmonic Approximation),是假设输入到输出的能量传递基于电路中电流、电压的傅里叶级数的基波分量,即将流经谐振网络的参数波形都视为正弦波,忽略其谐波分量。
虽然基波分析法能够使电路模型得到极大的简化,但不可避免还是存在差,例如当工作频率小于谐振频率时,副边输出电流工作在断续状态,建模精度有所下降。但 LLC 谐振变换器为了实现高变换效率一般工作在谐振变换点附近,此时基波分析法能够给出精确的结果。
在用 FHA 简化建模时,首先要做如下假设:
(1)理想元件。LLC 谐振电路中所有元器件都是理想器件;
(2)开关网络 2 组驱动信号占空比为 50%,并且工作在接近谐振频率;
(3)与负载并联的滤波电容 Cf 足够大,将输出电压的纹波忽略。
由开关电路工作原理可知,输入直流电压 Vin经开关电路逆变后被转化为方波电压 vs(t)。将 vs(t)进行傅里叶分解:
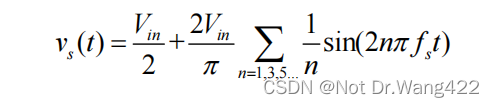
根据 FHA 的思想,逆变网络输出电压 vs(t)的基波分量 vs1(t)为:
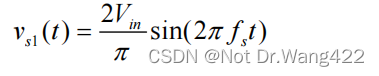
其中,Vin是输入直流的电压的幅值, ws =2pifs ,fs 为开关频率。
Vs1(t)为基波电压 vs1(t)的有效值,其大小为:

如建模前假设规定,变压器 T 为理想变压器,其变比为 n:1:1,输出滤波电容Cf足够大使输出电流纹波忽略。变换器输出电压 vo(t)=Vo,输出电流 io(t)=Io。vR(t)、iR(t)为变压器原边电压和电流。当 iR(t)>0 是, D1 导通,vR(t) =nVo;当 iR(t)<0 时,D2 导通,vR(t)=-nVo。

变压器原边输入电压 vR(t)(同时也是谐振网络的输出)是一个方波电压,其幅值为 nVo。由于谐振网络是线性网络,输入和输出信号形式相同[23]。谐振网络输入电压 vs1(t)是正弦波信号,其对应输出信号也应该是正弦波形式。对 vR(t)和 iR(t)进行傅里叶变换:
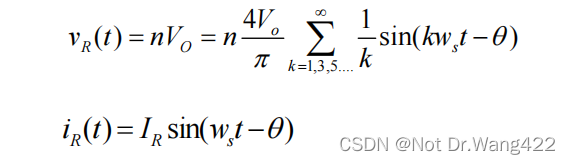
式中,IR为原边输入电流 iR(t)的幅值,θ为其初始相位。根据 FHA 思想建模,只有信号中的基波分量传递能量,取 VR1(t)的基波分量 vR1(t) :
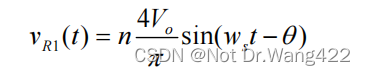
由上式可知,vR1(t)和 iR(t)相位相同,所以 LLC 谐振变换器的变压器 T 和整流滤波网络对于谐振网络来说呈阻性,其等效电阻 Re可表达为:
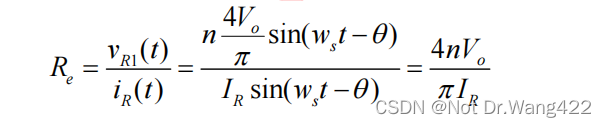
并且,根据建模前的假设条件,由于整流滤波电容 Cf足够大,整流网络的输出电流经 Cf 后使输出电流纹波被忽略,故只有直流分量流过负载 RL,变换器输出电流 Io可表达为:
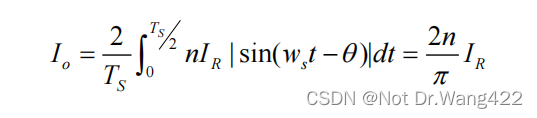
将式(2.10)代入式(2.9),可将等效电阻 Re简化为:
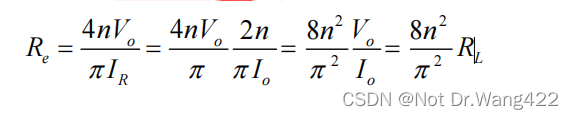
根据以上推导,用 FHA 思路以谐振网络为核心搭建的 LLC 谐振变换器模型如图 2-19 所示。其中开关网络输出电压 vs1(t)作为输入电压源,Re 表示变压器及整流滤波网络对谐振网络的负载特性。
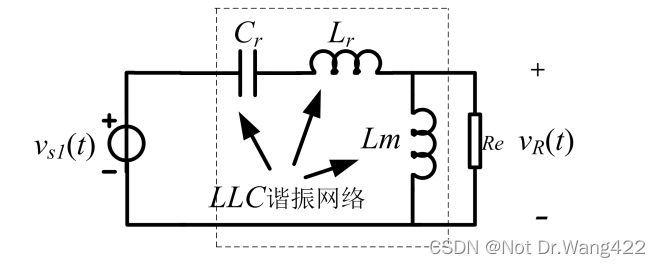
由图可知,LLC 谐振变换器等效电路阻抗 Zin可表达为:
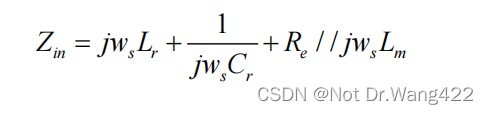
变换器谐振网络传递函数 H( jws ):
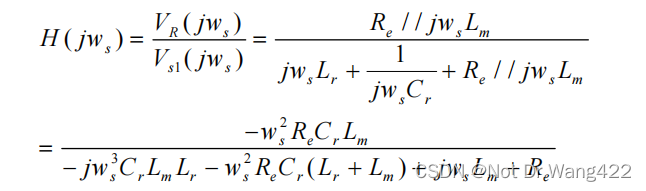
另外,LLC 谐振变换器的重要工作参数可表示为:
谐振电感 Lr和谐振电容 Cr的谐振角频率:
Lr、Cr和 Lm的谐振角频率:
谐振电路的特征阻抗 Zr为:
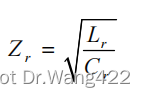
Q 为电路品质因数: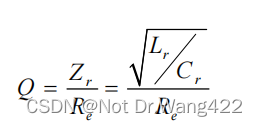
定义 Lm与 Lr之比λ:λ=Lm/Lr
根据 wr定义的频率归一化量为 fn: fn = ws / wr
将上述参数代入,用 Q、λ、fn表达,可得出式(2.13)的幅频及相频为:
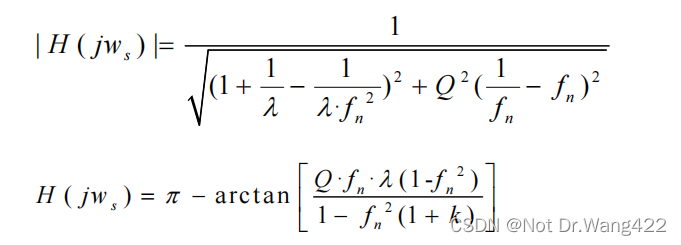
此外,通过建立 LLC 谐振变换器的等效电路模型,也就能对其稳压原理进行直观的解释

如上图所示,谐振网络输入电压 vs1=vs2+vR 。当 vs1 或者变换器输出负载发生变化时,会引起输出电压 vR变化。此时,通过改变频率,使 Lr和 Cr 的串联阻抗(jwsLr+1/jwsCr)的分压 vs2相应改变,最终使得输出电压 vR保持稳定。在本节中以基波分析法为基础的 LLC 谐振变换器主电路等效模型搭建完成。虽然基波分析法能够使电路模型得到极大的简化,但不可避免还是存在误差,例如当工作频率小于谐振频率时,副边输出电流工作在断续状态,建模精度有所下降。但变换器为了追求效率,稳态工作于谐振工作点附近,误差可忽略。