1.基本画图方式
MATLAB 的扩展性和机制独立的画图功能是一个极其重要的功能.这个功能使数据画图变得十分简单
.
画一个数据图
,
首先要创建两个向量,由
x, y
构成
,
然后使用
plot
函数. 例如
,
假设我们要画出函数
y=x²
-10x+10
的图象
,
定义域为[
0,10
]
.
只需要
3 个语句就可以画出此图
.
第二句用于计算
y
值
(
注意我们用的是数组运算符
,
所以可以对
x 的元素一一运算
.).
最后打印出此图
.
x=0:1:10;
y=x.^2-10*x+15;
plot(x,y);运行结果如图1所示:
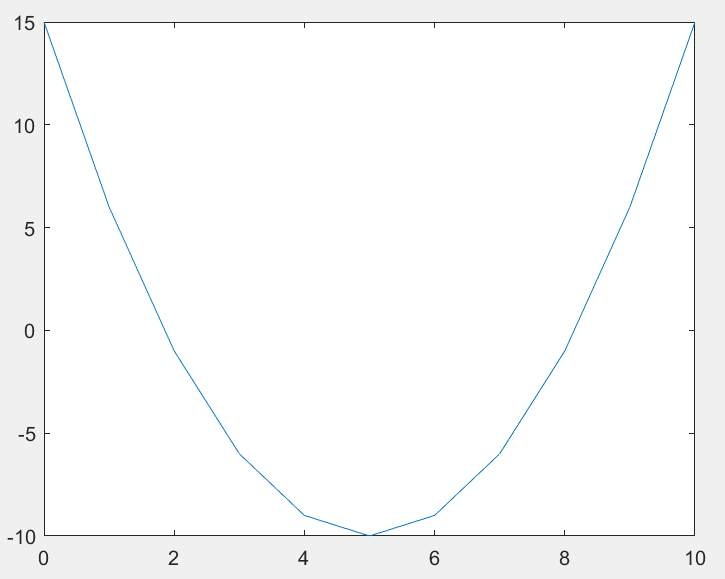
正如我们所看到的,
在
MATLAB
中画图是十分容易的
.只要任何一对向量的长度相同,那么它就可以就能可视化地画出来
.
但是这还不是最后的结果
,
因为它还没有标题
,
坐标轴标签, 网格线.给图增加标题和坐标轴标签将会用到 title, xlabel, ylable 函数。调用每个函数时将会有一个字符串,这个字符串包含了图象标题和坐标轴标签的信息。用 grid 命令可使网格线出现或消失在图象中,grid on 代表在图象中出现网格线,grid off 代表去除网格线。例如下面的语句将会产生带有标题,标签和网格线的函数图象。结果如图 2所示。
x=0:1:10;
y=x.^2-10*x+15;
plot(x,y);
title ('Plot of y=x.^2-10*x+15');
xlabel ('x');
ylabel ('y');
grid on;
在同一坐标内作出多个函数的图象的情况是十分常见的。假如,你要在同一坐标轴内作出 f(x)=sin2x 和他的微分函数的图象。它的微分式为
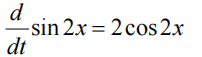
在同一坐标系内打印两个函数,我们必须产生一系列的 x
值和每一个函数分别对应的 y值。然后利用这些值画出图象,
plot
函数的格式如下所示:
x=0:pi/100:2*pi;
y1=sin(2*x);
y2=2*cos(2*x);
plot (x,y1,x,y2);所得图像如图3所示:

2.线的颜色,线的形式,符号形式和图例
MATLAB 允许程序员选择轨迹的颜色,轨迹的形式,和符号的类型.在 X,Y 向量参数后带有这些属性的字符串的 plot 函数,可以选择这些细节.这些属性字符串包括三类
1指定轨迹的颜色
,
2指定符号的类型
,
3指定线的类型
.
各种颜色,
符号和线的类型将在表1
中显示
.
表1 图象的颜色,标记(符号)类型,线型
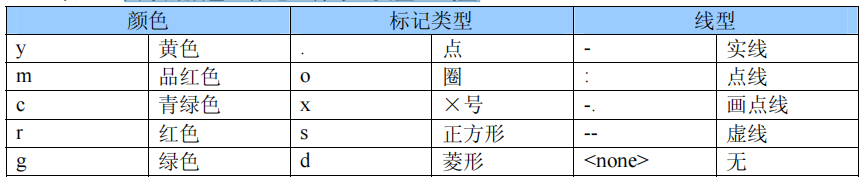

这些属性字符串可以任意的混合使用.
如果有多个函数
,每个函数都有它自己的属性字符串.例如
,
函数
y=x²
-10x+15
的图象
,
曲线为红色的虚线
,
重要的数值用蓝色的小圆圈表示
.
x=0:1:10;
y=x.^2 -10.*x +15;
plot(x,y,'r--',x,y,'bo');
我们可以用 legend 来制作图例。它的基本的形式如下
legend('string1','string2',...,pos)其中 string1,string2 等等是与轨迹标签名,而 pos 是一个整数,用来指定图例的位置。这些整数所代表的意义在表2列出。用 legend off 命令将能去除多余的图例。一个完整的图象例子将会显示图 4中,产生这个图象的语句如下所示。在同一坐标系内,显示了f(x)=sin2x 和它的微分函数的图象,用黑实线代表 f(x),用红虚线代表它的微分函数。图中有标题,坐标轴标签和网格线。
x=0:pi/100:2*pi;
y1=sin(2*x);
y2=2*cos(2*x);
plot(x,y1,'k-',x,y2,'b--');
title(' Plot of f(x)=sin(2x) and its derivative');
xlabel('x');
ylabel('y');
legend('f(x)','d/dx f(x)')
grid on;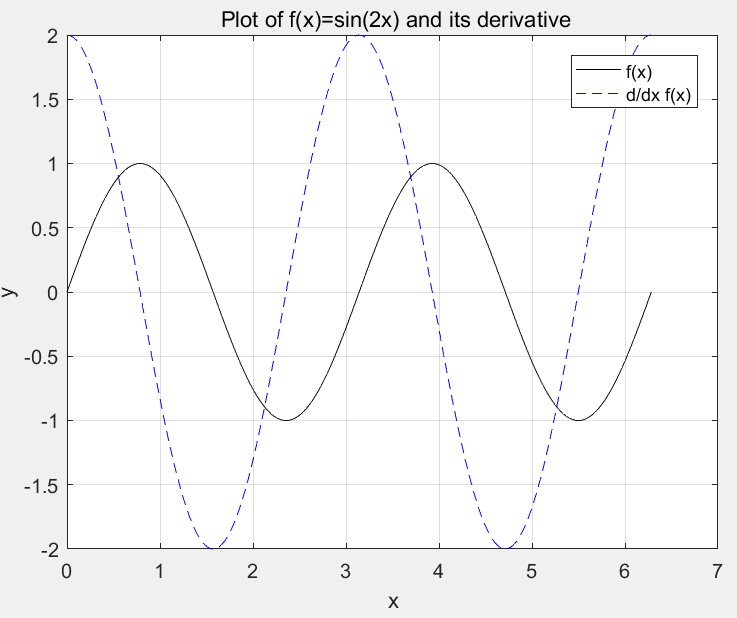
表2 pos值代表的含义
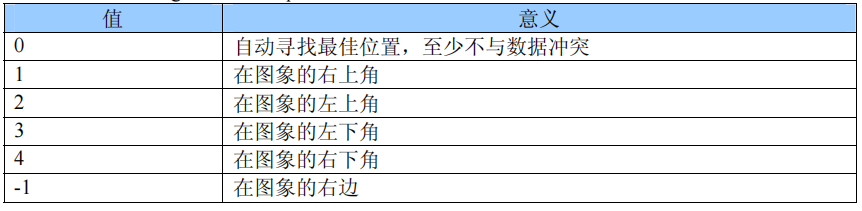
3对数坐标图
画图既可以用对数尺度,也可以用线性尺度。在 x,y 轴上使用这两种尺度的一种或两种可以组合形成
4
种不同的坐标系。每一种组合者有一个特定的函数。
1.plot
函数的
x,y
均用线性尺度
2.semilogy
函数
x
轴用对数尺度,
y
轴将用线性尺度
3.semilogx
函数
x
轴用线性尺度,
y
轴用对数尺度
4.loglog
函数两坐标轴将会都用对数尺度。
x=0:0.1:10;
y=(x-5).^2+1;
subplot(2,2,1)
plot(x,y)
title('plot(x,y)')
subplot(2,2,2)
semilogy(x,y)
title('semilogy(x,y)')
subplot(2,2,3)
semilogx(x,y)
title('semilogx(x,y)')
subplot(2,2,4)
loglog(x,y)
title('loglog(x,y)')这四个函数在意义上是等价的,只是坐标轴的类型不同。每一个图象的例子如图5所示。

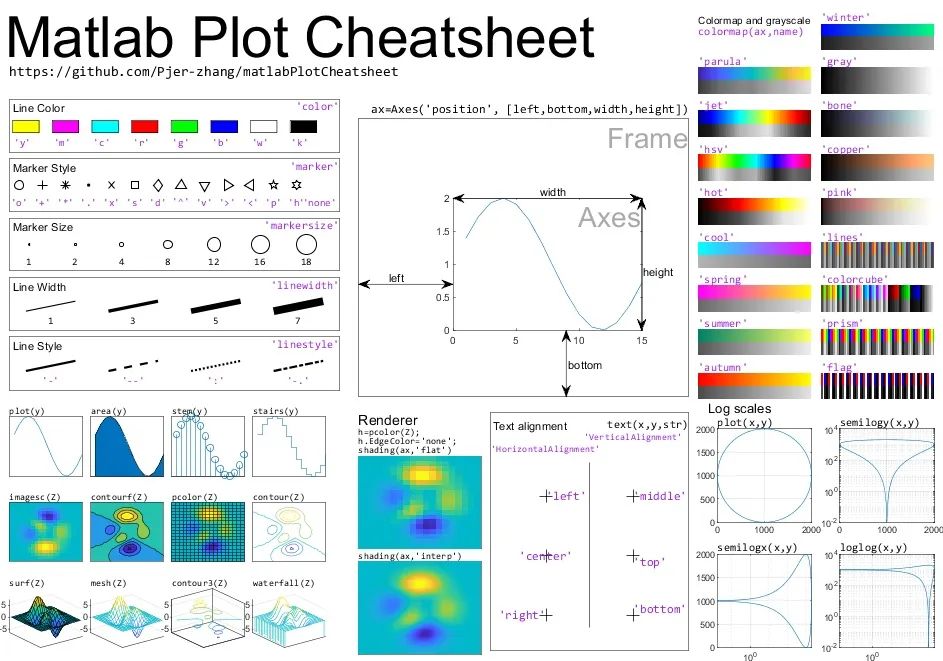
最后,分享一个大佬制作的matlab画图速查表(来源于微信公众号:空间物理)