1.文章信息
本次介绍的文章是2020年发表在IEEE 智能交通系统汇刊上的《T-GCN: A Temporal Graph Convolutional Network for Traffic Prediction》。
2.摘要
为了同时捕获空间和时间依赖性,本文提出了一种新的基于神经网络的交通流预测方法——时间图卷积网络(T-GCN)模型,该模型将图卷积网络(GCN)和门控循环单元(GRU)相结合。具体来说,GCN用于学习复杂拓扑结构以获取空间相关性,GRU用于学习交通数据的动态变化以获取时间相关性。然后,将T-GCN模型应用于基于城市路网的交通预测。实验证明,我们的T-GCN模型可以从交通数据中获得时空相关性,并且预测结果优于现实交通数据集上的最先进基线模型。
3.介绍
交通预测由于其复杂的时空依赖性,一直是一项具有挑战性的任务:
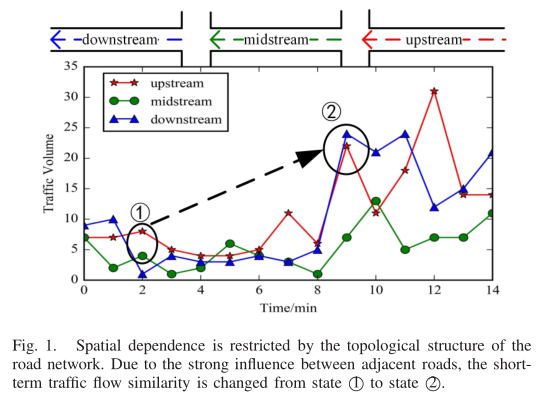
(1)空间依赖性。交通量的变化主要受城市路网拓扑结构的影响。上游道路交通状况通过传递效应影响下游道路交通状况,下游道路交通状况通过反馈效应[4]影响上游道路交通状况。如图1所示,由于相邻道路之间的影响较强,短期相似度由状态1(上游道路与中游道路相似)变为状态2(上游道路与下游道路相似)。
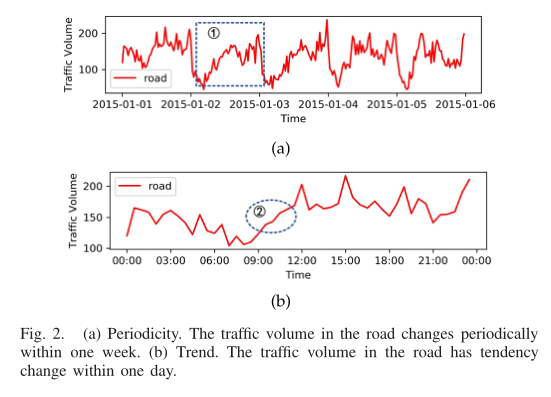
(2)时间依赖性。交通量随时间动态变化,主要表现为周期性和趋势性。如图2(a)所示,道路上的交通量在一周内呈周期性变化。如图2(b)所示,一天的交通量随时间变化;例如,当前的交通量受到前一刻甚至更长时间的交通状况的影响。
为了解决上述问题,本文主要贡献有:
(1) T-GCN模型集成了图卷积网络和门控循环单元。利用图卷积网络捕获道路网络的拓扑结构,建模道路网络的空间相关性。采用门控循环单元捕捉道路上交通数据的动态变化,建模时间依赖性。T-GCN模型也可以应用于其他时空预测任务。(2) T-GCN模型在不同预测视界下的预测结果均呈现稳态,说明T-GCN模型不仅可以实现短期预测,而且可以用于长期的交通预测任务。 (3)我们使用两个真实交通数据集来评估我们的方法。结果表明,与所有基线方法相比,该方法的预测误差减小了约1.5% ~ 57.8%,表明T-GCN模型在交通预测方面具有优势。
4.模型建立
问题定义:在本研究中,交通预测的目标是根据道路上的历史交通信息,预测一定时间内的交通信息。在我们的方法中,交通信息是一个一般的概念,可以是交通速度、交通流量或交通密度。在不失一般性的前提下,我们在实验部分以交通速度作为交通信息的例子。
定义1:我们使用一个未加权图G = (V, E)来描述道路网络的拓扑结构,我们将每条道路视为一个节点,其中V是道路节点的集合,V = {v1, v2,····,vN}, N是节点的数量,E是边的集合。用邻接矩阵A表示道路之间的连通性,A∈R^(N×N)邻接矩阵只包含0和1的元素。如果两条路之间没有联系,则元素为0;有联系表示为1。
定义2:特征矩阵X^(N×P)。我们将路网中的交通信息作为网络中节点的属性特征,表示为X∈R^(N×P), P表示节点属性特征的个数(历史时间序列的长度),Xt∈R^(N×i)表示i时刻每条道路上的速度。同样,节点属性特征可以是交通速度、交通流量、交通密度等任意交通信息。
因此,时空交通预测问题可以认为是在路网拓扑G和特征矩阵X的前提下,学习映射函数f,然后计算接下来T时刻的交通信息,如式1所示:
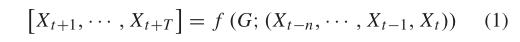
其中n是历史时间序列的长度,T是需要预测的时间序列的长度。
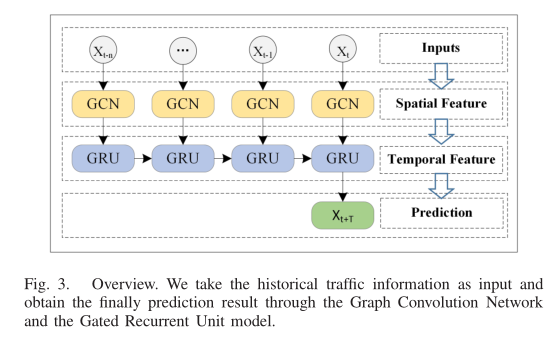
概述:在本节中,我们描述了如何使用T-GCN模型来实现基于城市道路的交通预测任务。具体来说,T-GCN模型由图卷积网络和门控循环单元两部分组成。如图3所示,我们首先使用历史n时间序列数据作为输入,利用图卷积网络捕获城市道路网络的拓扑结构,获得空间特征。其次,将获得的具有空间特征的时间序列输入门控循环单元模型,通过单元间的信息传递获取动态变化,获取时间特征;最后,我们通过全连接层得到结果。
方法:1)空间依赖建模:GCN模型已成功应用于文档分类、无监督学习和图像分类等领域。给定邻接矩阵A和特征矩阵X, GCN模型在傅里叶域中构造一个滤波器。该滤波器作用于图的节点上,通过节点的一阶邻域捕获节点之间的空间特征,然后将多个卷积层堆叠起来构建GCN模型,表示为:
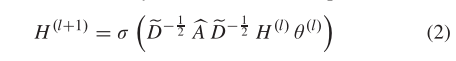
在本研究中,选择2层GCN模型来获得空间相关性,其可表示为:
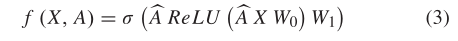
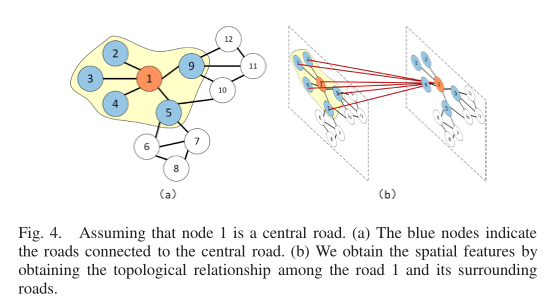
综上所述,我们使用GCN模型从交通数据中学习空间特征。如图4所示,假设节点1为中心道路,GCN模型可以得到中心道路与其周围道路之间的拓扑关系,并对路网拓扑结构和道路上的属性进行编码,进而得到空间依赖关系。
2)时间依赖模型:选择GRU模型从交通数据中获得时间依赖性。如图5所示,ht−1表示t-1时刻的隐藏状态;Xt为t时刻的交通信息;Rt为复位门,用于控制对前一时刻状态信息的忽略程度;Ut为更新门,用于控制前一时刻的状态信息进入当前状态的程度;Ct为t时刻存储的内存内容;t时刻的输出状态。GRU以t-1时刻的隐藏状态和当前的流量信息作为输入,得到t时刻的流量信息。该模型在捕获当前时刻的交通信息的同时,仍然保留了历史交通信息的变化趋势,具有时间依赖性的捕获能力。
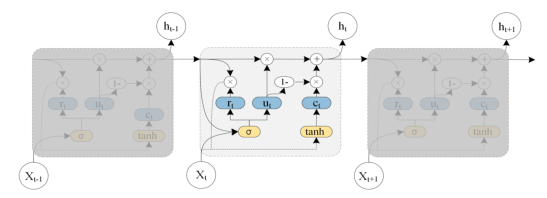
3)时序图卷积网络:为了从交通数据中同时获取空间和时间依赖性,我们提出了一种基于图卷积网络和门控循环单元的时间图卷积网络模型(T-GCN)。如图6所示,左侧为时空流量预测过程,右侧为t- gcn单元的具体结构,ht−1为t-1时刻的输出,GC为图卷积过程,ut、rt为t时刻的更新门和复位门,ht为t时刻的输出。具体计算过程如下图所示。f (A, Xt)表示图卷积过程,定义如式3。*表示逐点乘法。W和b代表训练过程中的权重和偏差。
综上所述,T-GCN模型可以处理复杂的空间依赖性和时间动态。一方面,利用图卷积网络捕获城市道路网络的拓扑结构,获得空间相关性;另一方面,采用门控循环单元捕捉道路上交通信息的动态变化,获得时间依赖关系,最终实现交通预测任务。
4)损失函数:在训练过程中,目标是最小化道路上真实交通速度与预测值之间的误差。我们用Yt和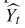 分别表示实际交通速度和预测速度。T-GCN模型的损失函数如式8所示。第一项用于最小化实际交通速度与预测之间的误差。第二项Lreg是L2正则化项,有助于避免过拟合问题,λ是一个超参数。
分别表示实际交通速度和预测速度。T-GCN模型的损失函数如式8所示。第一项用于最小化实际交通速度与预测之间的误差。第二项Lreg是L2正则化项,有助于避免过拟合问题,λ是一个超参数。
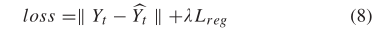
5.实验结果与分析
1.数据说明:在本节中,我们评估了T-GCN模型在两个真实数据集上的预测性能:SZ-taxi数据集和Los-loop数据集。因为这两个数据集都与交通速度有关。在不失一般性的前提下,我们在实验部分采用交通速度作为交通信息。
(1) SZ-taxi。该数据集由深圳市2015年1月1日至1月31日的出租车轨迹组成。我们选取罗湖区156条主要道路作为研究区域。实验数据主要包括两部分。一种是156*156的邻接矩阵,描述道路之间的空间关系。每一行表示一条道路,矩阵中的值表示道路之间的连通性。另一个是特征矩阵,它描述了每条道路上的速度随时间的变化。每一行代表一条路;每一列是不同时间段道路上的交通速度。我们每15分钟统计每条道路上的交通速度。
(2) Los-loop。该数据集由环路检测器实时从洛杉矶县的高速公路上收集。我们选取了207个传感器及其2012年3月1日至3月7日的交通速度。我们每5分钟统计一次交通速度。数据由邻接矩阵和特征矩阵组成。邻接矩阵由交通网络中传感器之间的距离来计算。由于Losloop数据集包含一些缺失数据,我们使用线性插值方法来填充缺失值。
在实验中,将输入数据归一化到区间[0,1]。另外,80%的数据作为训练集,剩下的20%作为测试集。
2.评价指标:我们使用五个指标来评估T-GCN模型的预测性能:

M为时间样本数;N是道路的数量;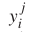 和
和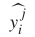 表示真实交通信息,预测第i条道路的第j个时间样本之一,Y和
表示真实交通信息,预测第i条道路的第j个时间样本之一,Y和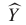 分别代表
分别代表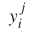 和
和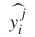 的集合,
的集合,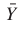 是Y的平均值。具体来说,采用RMSE和MAE来衡量预测误差,数值越小,预测效果越好。准确度用于检测预测精度,数值越大,预测效果越好。R2和var计算相关系数,相关系数衡量的是预测结果对实际数据的反映能力,值越大,预测效果越好。
是Y的平均值。具体来说,采用RMSE和MAE来衡量预测误差,数值越小,预测效果越好。准确度用于检测预测精度,数值越大,预测效果越好。R2和var计算相关系数,相关系数衡量的是预测结果对实际数据的反映能力,值越大,预测效果越好。
3.模型参数选择:
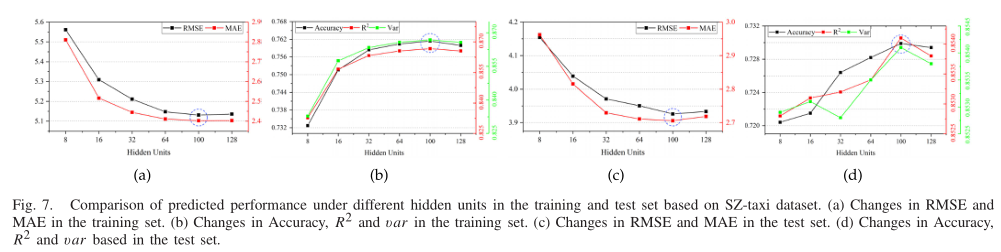
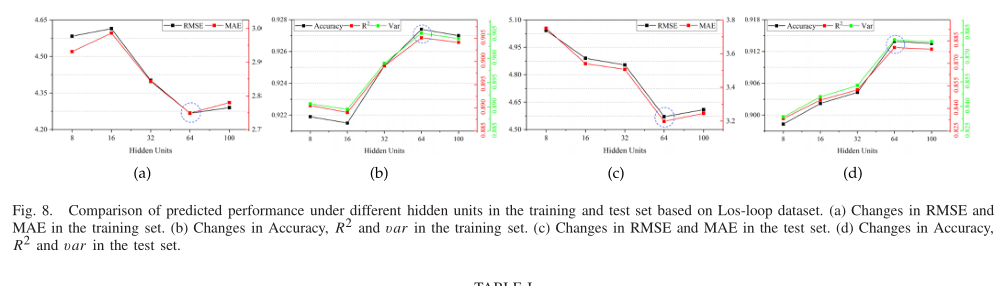
(1)超参数T-GCN模型的超参数主要包括:学习率、批大小、训练历元、隐藏单元数。在实验中,我们手动调整并设置学习率为0.001,批大小为32,训练epoch为5000。隐藏单元数是T-GCN模型中一个非常重要的参数,不同的隐藏单元数会对预测精度产生很大的影响。为了选择最佳值,我们对不同的隐藏单元进行实验,并通过比较预测结果来选择最优值。在我们的实验中,对于SZ-taxi数据集,我们从[8,16,32,64,100,128]中选择隐藏单元数,并分析其预测精度的变化。如图7所示,横轴表示隐藏单元的数量,纵轴表示不同指标的变化。图7(a)显示了训练集中不同隐藏单元的RMSE和MAE结果。可以看出,当数值为100时,误差最小。图7(b)显示了不同隐藏单元的精度,R2, a n d var的变化。图7(c)和7(d)显示了测试集中的结果。同样,当数字为100时,结果达到最大值。综上所述,当数量设置为100时,预测结果更好。随着隐藏单元数量的增加,预测精度先提高后降低。这主要是因为当隐藏单元大于一定程度时,模型复杂度和计算难度大大增加,导致训练数据出现过拟合。因此,我们在SZ-taxi数据集上的实验中将隐藏单元的数量设置为100。同样,Los-loop的结果如图8(a), 8(b), 8(c), 8(d)所示。可以看出,当隐藏单元数为64时,预测精度最高,预测误差最小。对于输入层,在训练过程中以训练数据集(总数据的80%)为输入,其余数据作为测试过程的输入。T-GCN模型使用Adam优化器进行训练。
4.实验结果:表1比较了T-GCN模型与以下基线方法的性能。
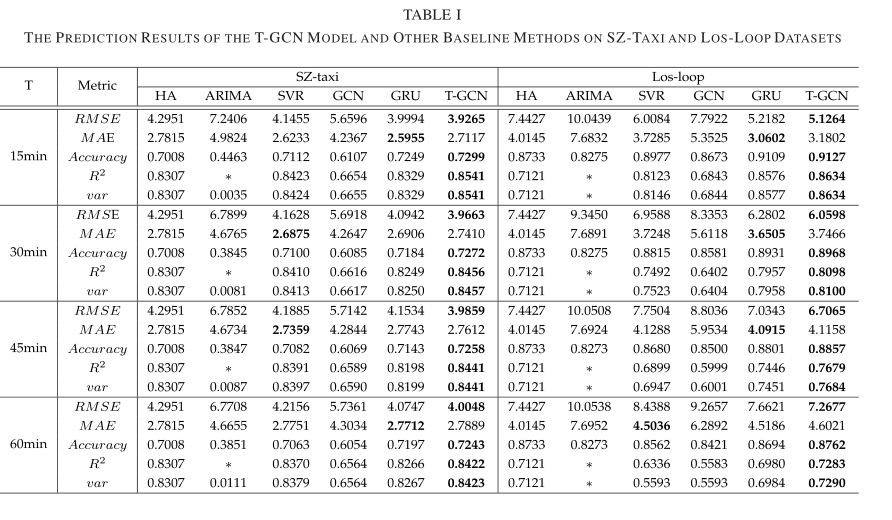
表一显示了T-GCN模型和其他基线方法在SZ-taxi和Los-loop数据集上对15分钟、30分钟、45分钟和60分钟预测任务的性能。*表示这些值小到可以忽略不计,表明模型的预测效果很差。可以看出,T-GCN模型在所有预测视界的几乎所有评价指标下都获得了最好的预测性能,证明了其对时空交通预测任务的有效性。(1)预测精度高。我们可以发现,基于神经网络的方法,包括T-GCN模型、GRU模型,强调时间特征建模的重要性,通常比其他基线(如HA模型、ARIMA模型和SVR模型)具有更好的预测精度。
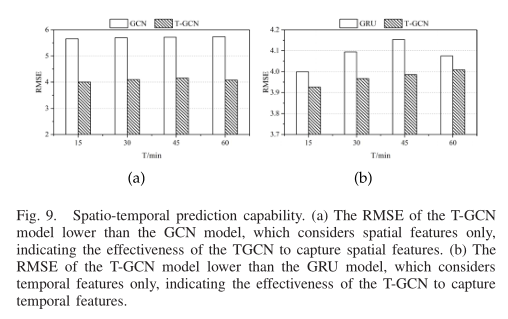
(2)时空预测能力。为了验证T-GCN模型是否具有从交通数据中描绘时空特征的能力,我们将T-GCN模型与GCN模型和GRU模型进行了比较。如图9所示,我们可以清楚地看到,基于时空特征的方法(T-GCN)比基于单因素的方法(GCN, GRU)具有更好的预测精度,说明T-GCN模型能够从交通数据中捕捉到时空特征。
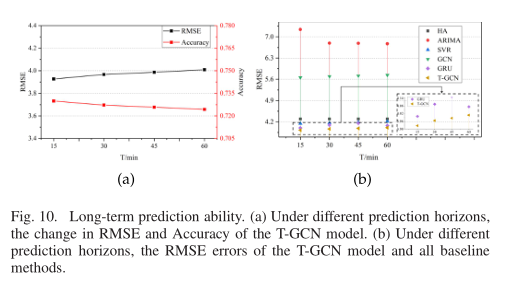
(3)长期预测能力。无论视界如何变化,T-GCN模型通过训练都能获得最好的预测性能,预测结果的变化趋势较小,说明我们的方法对预测视界不敏感。因此,我们知道T-GCN模型不仅可以用于短期预测,也可以用于长期预测。图10(a)显示了不同预测层位下RMSE和Accuracy的变化,分别表示T-GCN模型的预测误差和精度。可以看出,误差增加和精度下降的趋势较小,具有一定的稳定性。图10(b)显示了不同视界上基线的RMSE比较。我们观察到,T-GCN模型无论预测视界如何,都能获得最好的结果。
在实验过程中,我们在数据中加入了两种常见的随机噪声。随机噪声服从高斯分布N∈(0,σ 2), σ∈(0.2,0.4,0.8,1,2)和泊松分布P(λ), λ∈(1,2,4,8,16)。然后,我们将噪声矩阵的值归一化到0到1之间。使用不同的评估指标,结果如下所示。图11(a)显示了在SZ-taxi数据集上添加高斯噪声的结果,其中横轴表示σ,纵轴表示各评价指标的变化,不同颜色表示不同指标。同样,图11(b)显示了在SZ-taxi数据集上添加泊松噪声的结果。图11(c)和图11(d)是在Losloop数据集上添加高斯噪声和泊松噪声后的结果。可以看出,无论噪声分布如何,指标的变化都很小。因此,T-GCN模型是鲁棒的,能够处理高噪声问题。
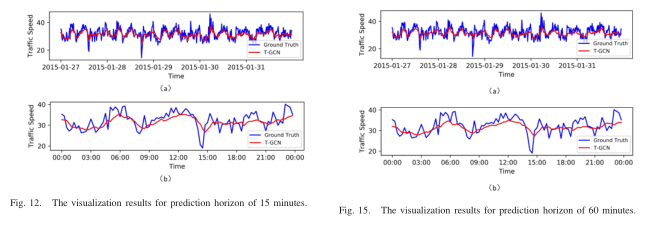
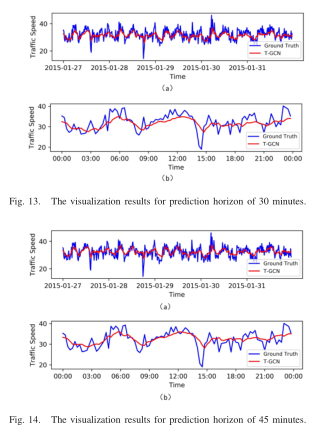
5)模型解释:为了更好地理解T-GCN模型,我们在SZ-taxi数据集中选择一条道路,并将测试集的预测结果可视化。图12、图13、图14和图15分别为15分钟、30分钟、45分钟和60分钟预测视界的可视化结果。这些结果表明:(1) T-GCN模型在局部极小/极大值处预测较差。我们推测主要原因是GCN模型在傅里叶域中定义了一个平滑滤波器,并通过不断移动滤波器来捕获空间特征。这一过程导致整体预测结果变化较小,使峰值更平滑。(2)“零出租车值”导致真实交通信息与预测结果存在一定误差。零出租车值是指由于道路上没有出租车,其真实值不为零的交通特征矩阵将被设为零的现象。(3)无论预测视界如何,T-GCN模型总能获得更好的预测结果。T-GCN模型可以捕获道路交通信息的时空特征,得到道路交通信息的变化趋势。此外,T-GCN模型检测高峰时段的开始和结束,预测结果与实际交通速度模式相似。这些性质有助于预测交通拥堵和其他交通现象。
6.结论
本研究开发了一种基于神经网络的交通预测方法T-GCN,该方法将GCN和GRU相结合。我们使用图网络对城市道路网络进行建模,图上的节点表示道路,边表示道路之间的连接关系,道路上的交通信息描述为图上节点的属性。一方面,利用GCN捕获图的空间拓扑结构,获得图的空间相关性;另一方面,引入GRU模型捕捉节点属性的动态变化,获得节点属性的时间依赖性。最后将T-GCN模型应用于交通时空预测。在两个真实交通数据集上进行评估,并与HA模型、ARIMA模型、SVR模型、GCN模型和GRU模型进行比较,T-GCN模型在不同的预测水平下表现出更好的性能。此外,微扰分析说明了我们的方法的鲁棒性。综上所述,T-GCN模型成功地捕捉了交通数据的时空特征,可应用于其他时空任务。
Attention
欢迎关注微信公众号《当交通遇上机器学习》!如果你和我一样是轨道交通、道路交通、城市规划相关领域的,也可以加微信:Dr_JinleiZhang,备注“进群”,加入交通大数据交流群!希望我们共同进步!