目录

一.引言

二.GSU  结构分析

1.Input Layer 输入层

2.Embedding Layer 嵌入层

3.Pooling Layer 池化层

4.MLP 深层网络

5.Soft Search 软搜索

三.GSU 结构实现 

1.Init 初始化

2.Build 构建

3.call 调用

4.GSU Layer 完整代码

四.GSU 模型训练

1.Input Layer

2.GSU Layer

3.GSU Model

4.模拟序列样本生成

5.模型 Fit

五.Soft Search 软搜索

1.获取 Embedding 参数

2.Soft Search

3.Soft Search 取 Top-K 

六.总结

---

一.引言

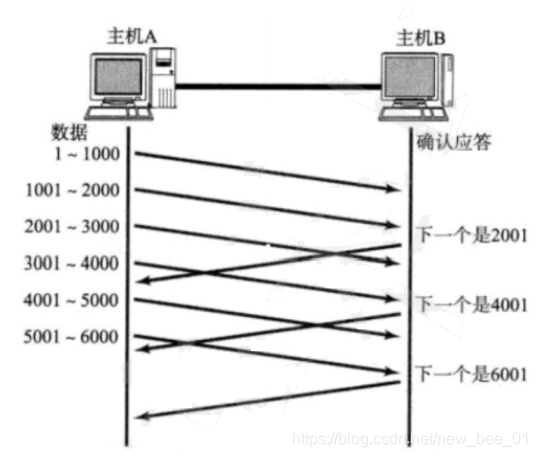
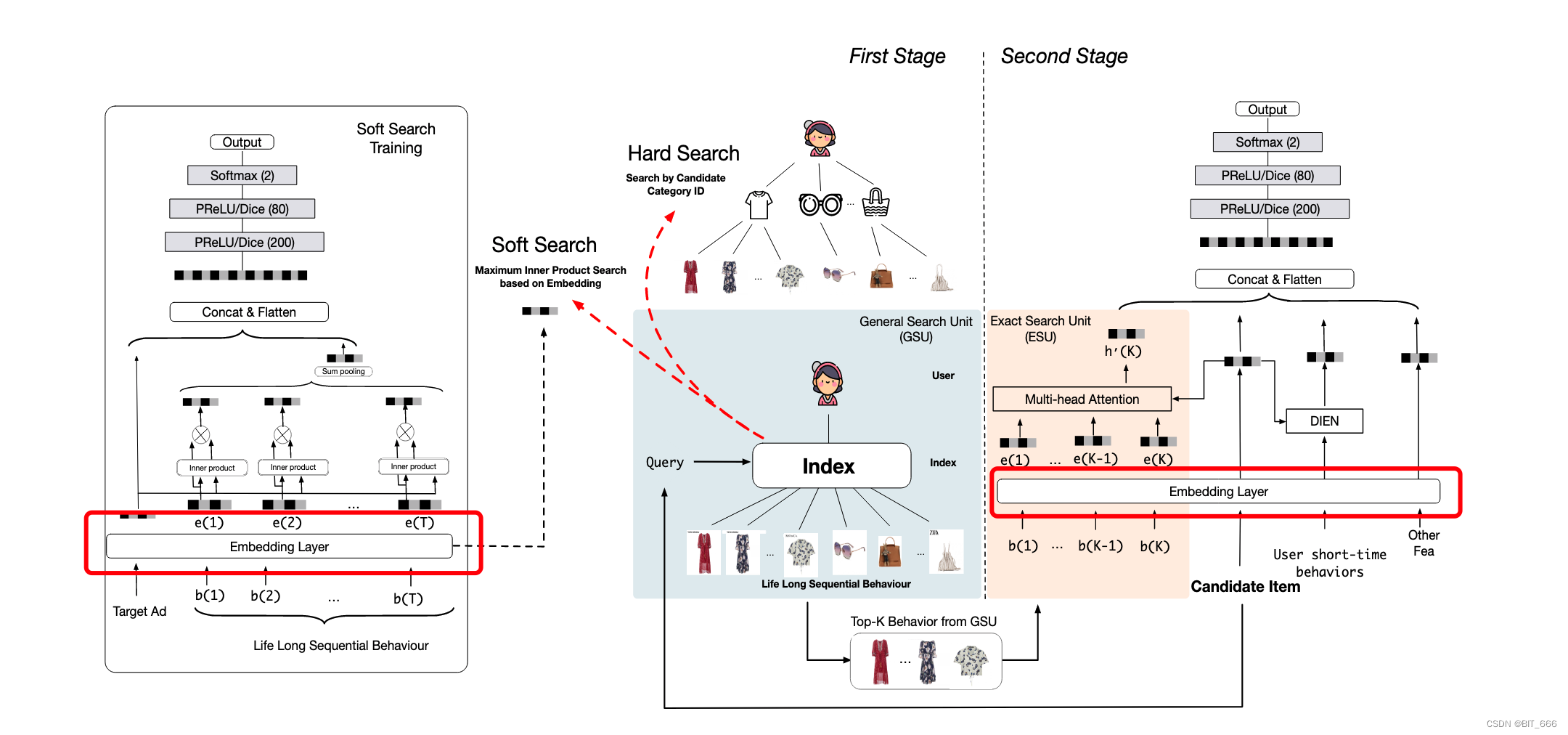
SIM 引入两阶段兴趣搜索，通过 GSU 通用搜索单元从长序列中快速匹配与 Item 相关的用户长期兴趣生成相关子用户序列 SBS，并通过 ESU 模拟候选  Item 与 SBS 之间的精确关系。其中 GSU 模块一般有 Soft Search 和 Hard Search 两种方法，下面基于 keras 简单实现下 Soft Search 软搜索并根据内积生成 SBS。

 

二.GSU  结构分析

GSU - General search Unit 指的是 SIM 模型的通用搜索模块单元，关于 SIM 的具体论文细节大家可以参考：SIM 论文笔记，本文主要基于 keras 实现简单 GSU 的 Soft Search，其模块如下图红框所示。

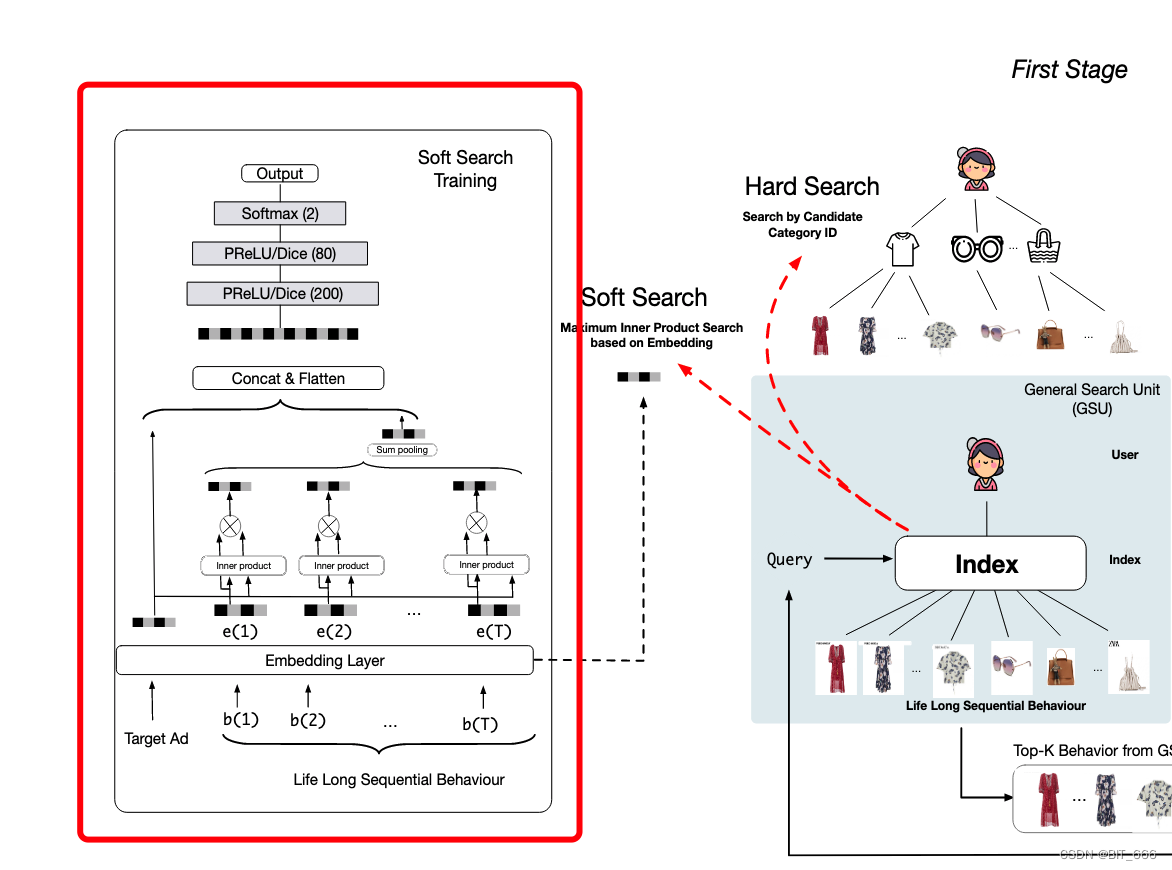
1.Input Layer 输入层

输入层包括 Target Ad 目标广告以及用户对应的长期序列行为，论文中认为 <= 14 天的行为为短期行为，> 14 天发生的行为为长期行为，并构造了 d-category metrics 进行了模型评估。

2.Embedding Layer 嵌入层

将上述 Ad-id 以及 b(i) 对应的 good-id lookup 获取对应 Embedding 嵌入。

Tips：

论文中认为用户长期行为与短期行为的分布不同，所以长期行为的 Embedding Layer 和短期行为对应的 Embedding Layer 并不共享，如下图红框所示，虽然 id 集合相同，但是 Embedding Layer 是分开构建的。

 

3.Pooling Layer 池化层

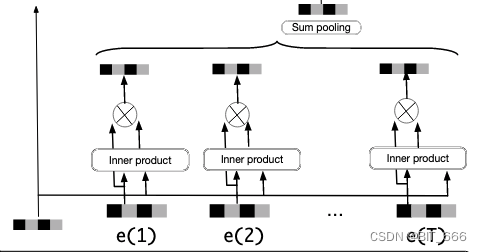
这里用长序列个每个 good Embedding 向量与 target Ad 的 Embedding 向量内积得到权重 Wi，然后 Wi 元素乘对应 good Embedding 做加权的 Sum Pooling，当然大家也可以尝试例如 Mean Pooling 这样的池化方式。

4.MLP 深层网络

最后一步遵循传统的 MLP 范式，将 Target Ad 的 Embedding 与长序列 Sum Pooling 得到的 Embedding 一起 Concat 传给 MLP 层，其层数分别为 200、80、2，与 DIN 类似，采用了 PRelu / Dice 激活函数，最后的 softmax 输出结果。  

5.Soft Search 软搜索

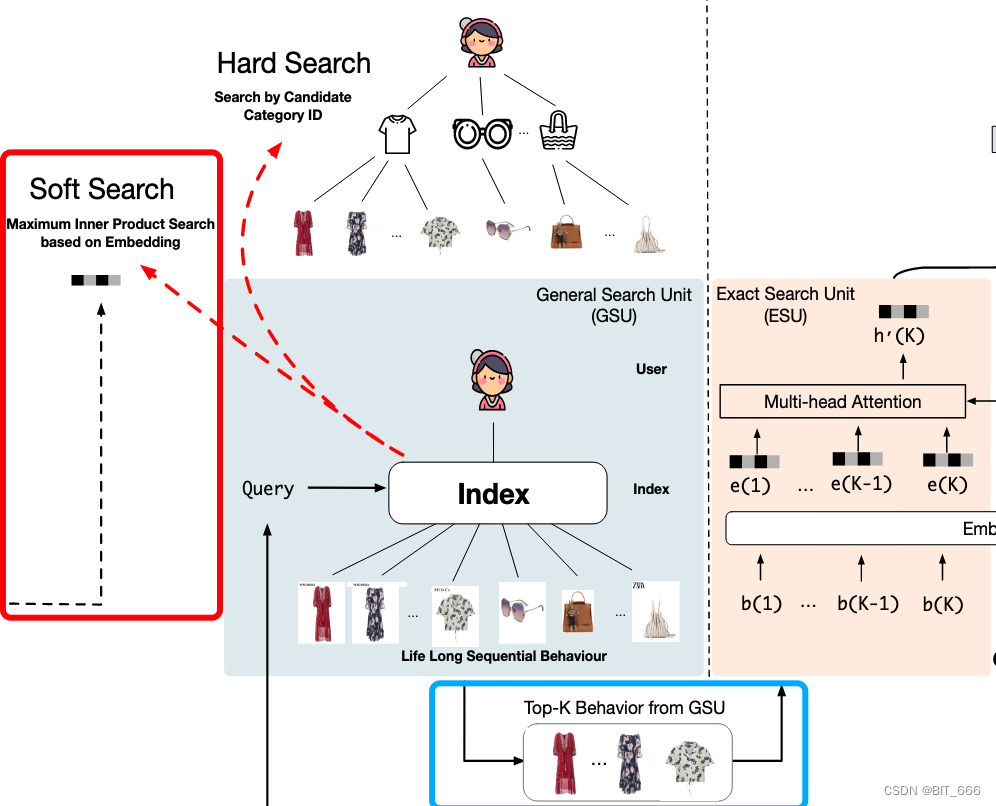
Soft Search 通过 Maximum Inner Product 最大内积搜索与 Query 相近的 Top-K Behavior In GSU，其中 DIN、DIEN 使用的序列长度一般为 150，这里论文 K 选择 150-200 的范围。 

 

三.GSU 结构实现 

全部依赖如下，其中 Dice 激活可以参考：DIN 实现 By Keras。

import numpy as np
import tensorflow as tf
from tensorflow.keras import Model
from tensorflow.keras.layers import Dense, Layer
from tensorflow.python.keras import Input
from tensorflow.python.ops.init_ops import TruncatedNormal
from DIN import Dice
from tensorflow.keras import backend as K
import heapq

1.Init 初始化

class GSULayer(Layer):

    def __init__(self, N=10000, embedding_dim=8, pooling_mode='sum', **kwargs):

        # 序列相关
        self.N = N
        self.embedding_dim = embedding_dim
        self.pooling_mode = pooling_mode
        self.T = None

        # 参数矩阵
        self.kernel = None
        self.weight_normalization = True

        self.DNN_3 = None
        self.DNN_2 = None
        self.DNN_1 = None

        super(GSULayer, self).__init__(**kwargs)

根据上面分析的 GSU Soft Search 模块，初始化定义如下变量： 

N - 商品库大小

embedding_dim - 嵌入向量维度

pooling_mode - [sum、mean] 求和与求平均

T - 用户序列长度

kernel - Embedding Layer 

weight_normalization - 权重是否归一化

DNN_I - MLP 对应的 200、80、2 的隐层

2.Build 构建

    def build(self, input_shape):
        # 获取序列长度
        history_shape, candidate_shape = input_shape
        self.T = history_shape[1]

        # N x embedding_dim 的参数矩阵
        self.kernel = self.add_weight(name='kernel',
                                      shape=(self.N, self.embedding_dim),
                                      initializer=TruncatedNormal,
                                      trainable=True)

        # 构建 DNN
        self.DNN_1 = Dense(200, activation=Dice())
        self.DNN_2 = Dense(80, activation=Dice())
        self.DNN_3 = Dense(1, activation='sigmoid')

        super(GSULayer, self).build(input_shape)

build 函数主要实现上述 init 变量的初始化，这里模型采用多输入模式，所以 history_shape 和 candidate_shape 是分开的，通过 history_shape 可以解析得到 T 序列长度。向量层大小为 N x embedding_dim，Dense 层的最后一层与原文略有不同，文章采用 Dense(2) + Softmax 的方式，这里采用 Dense(1) + Sigmoid 的方式。

3.call 调用

• 获取 Item、History 嵌入

    # 1.获取历史行为、候选集 Embedding 5x100x8, 5x1x8
    _history, _candidate = inputs  # [None, 10] [None, 1]
    # [None, T] => [None, T, embedding_dim]
    history_emd = tf.nn.embedding_lookup(self.kernel, _history)

    # [None, 1] => [None, 1, embedding_dim] => [None, T, embedding_dim]
    candidate_emb = tf.nn.embedding_lookup(self.kernel, _candidate)
    repeat_candidate_emb = K.repeat_elements(candidate_emb, self.T, axis=1)

直接 lookup 得到对应 Embedding 嵌入。

• Item 与 Good 计算内积

    # 内积计算权重
    dot_weights = tf.multiply(history_emd, repeat_candidate_emb)
    dot_weights = tf.reduce_sum(dot_weights, axis=2)

    if self.weight_normalization:
        dot_weights = tf.nn.softmax(dot_weights)

计算内积获得每个 Good 对应的权重 W，并根据参数决定是否归一化。

• 加权求和

    # 对 History 加权
    dot_weights = tf.reshape(dot_weights, [-1, self.T, 1])
    add_weights = history_emd * dot_weights

    # Sum Pooling
    if self.pooling_mode == "sum":
        pooling_output = tf.reduce_sum(add_weights, axis=1)
    else:
        pooling_output = tf.reduce_mean(add_weights, axis=1)

加权相乘后进行 pooling 操作，论文中采用 sum-pooling 求和方式池化。

• Concat && MLP

    # Concat
    candidate_emb = tf.reshape(candidate_emb, shape=(-1, self.embedding_dim))
    concat = tf.concat([candidate_emb, pooling_output], axis=-1)

    _output = self.DNN_1(concat)
    _output = self.DNN_2(_output)
    _output = self.DNN_3(_output)

Concat + MLP 的经典推荐模型范式，这里 DNN 也可以采用三层嵌套的写法。

4.GSU Layer 完整代码

class GSULayer(Layer):

    def __init__(self, N=10000, embedding_dim=8, pooling_mode='sum', **kwargs):

        # 序列相关
        self.N = N
        self.embedding_dim = embedding_dim
        self.pooling_mode = pooling_mode
        self.T = None

        # 参数矩阵
        self.kernel = None
        self.weight_normalization = True

        self.DNN_3 = None
        self.DNN_2 = None
        self.DNN_1 = None

        super(GSULayer, self).__init__(**kwargs)

    def build(self, input_shape):
        # 获取序列长度
        history_shape, candidate_shape = input_shape
        self.T = history_shape[1]

        # N x embedding_dim 的参数矩阵
        self.kernel = self.add_weight(name='kernel',
                                      shape=(self.N, self.embedding_dim),
                                      initializer=TruncatedNormal,
                                      trainable=True)

        # 构建 DNN
        self.DNN_1 = Dense(200, activation=Dice())
        self.DNN_2 = Dense(80, activation=Dice())
        self.DNN_3 = Dense(1, activation='sigmoid')

        super(GSULayer, self).build(input_shape)

    def call(self, inputs, **kwargs):
        # 1.获取历史行为、候选集 Embedding 5x100x8, 5x1x8
        _history, _candidate = inputs  # [None, 10] [None, 1]
        # [None, T] => [None, T, embedding_dim]
        history_emd = tf.nn.embedding_lookup(self.kernel, _history)

        # [None, 1] => [None, 1, embedding_dim] => [None, T, embedding_dim]
        candidate_emb = tf.nn.embedding_lookup(self.kernel, _candidate)
        repeat_candidate_emb = K.repeat_elements(candidate_emb, self.T, axis=1)

        # 内积计算权重
        dot_weights = tf.multiply(history_emd, repeat_candidate_emb)
        dot_weights = tf.reduce_sum(dot_weights, axis=2)

        if self.weight_normalization:
            dot_weights = tf.nn.softmax(dot_weights)

        # 对 History 加权
        dot_weights = tf.reshape(dot_weights, [-1, self.T, 1])
        add_weights = history_emd * dot_weights

        # Sum Pooling
        if self.pooling_mode == "sum":
            pooling_output = tf.reduce_sum(add_weights, axis=1)
        else:
            pooling_output = tf.reduce_mean(add_weights, axis=1)

        # Concat
        candidate_emb = tf.reshape(candidate_emb, shape=(-1, self.embedding_dim))
        concat = tf.concat([candidate_emb, pooling_output], axis=-1)

        _output = self.DNN_1(concat)
        _output = self.DNN_2(_output)
        _output = self.DNN_3(_output)

        return _output

    def compute_output_shape(self, input_shape):
        return input_shape[0][0], 1

四.GSU 模型训练

下面基于 GSU Layer 与模拟输入进行 Soft Search。

1.Input Layer

    # 批次大小、序列长度、商品类目
    batch_size, T, N = 5, 10000, 1000000

    # 多输入模型
    historyForGSU = Input(shape=(T,), dtype='int32', name='history')
    candidateForGSU = Input(shape=(1,), dtype='int32', name='candidate')

历史行为序列长度为 T，候选集长度为 1，论文中候选集的长度可以达到 54000，是先前 MIMN 记忆网络的 54x。

2.GSU Layer

    # Sum Pooling
    GSU = GSULayer(N=N, embedding_dim=8, pooling_mode='sum', name="GSU")
    outputByGSU = GSU([historyForGSU, candidateForGSU])

基础的多输入模型，采用 sum pooling。

3.GSU Model

    # 交叉熵二分类模型
    GSU_model = Model(inputs=[historyForGSU, candidateForGSU], outputs=[outputByGSU])
    GSU_model.compile(optimizer='rmsprop',
                      loss={'GSU': 'binary_crossentropy'},
                      loss_weights={'GSU': 1})
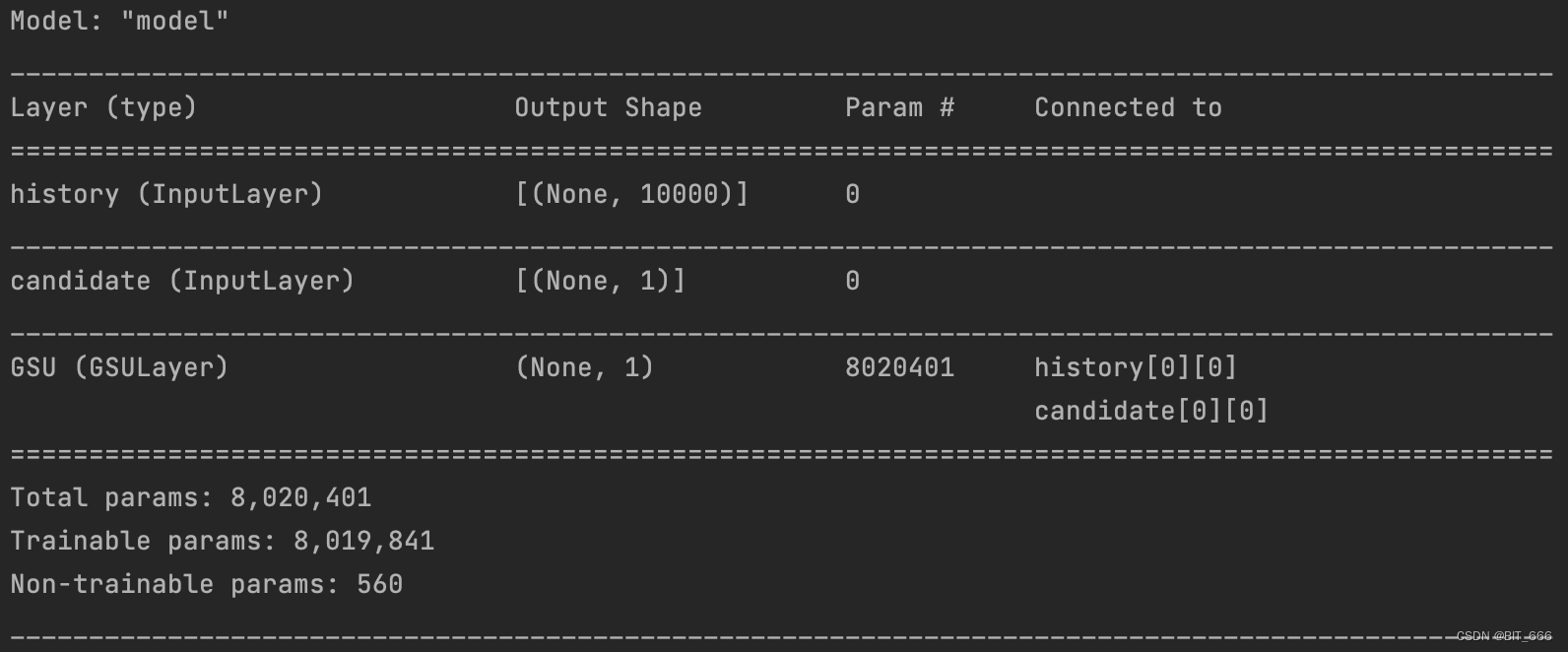
    GSU_model.summary()

添加损失函数与优化器，模型 summary 如下，论文中嵌入维度为 4，这里嵌入维度为 8，可以看到随着商品库数量的增加，模型参数的数量也很可观。

 

4.模拟序列样本生成

def genSamplesWithLabel(batch_size=5, T=10, N=1000, seed=0):
    np.random.seed(seed)
    # 用户历史序列
    user_history = np.random.randint(0, N, size=(batch_size, T))
    # 候选 Item
    user_candidate = np.random.randint(0, N, size=(batch_size, 1))
    # Labels
    sample_labels = np.random.randint(0, 2, size=batch_size)
    return user_history, user_candidate, sample_labels

# 用户历史行为序列 && 候选商品 ID
history, candidate, labels = genSamplesWithLabel(batch_size, T, N)

样本样例如下：

 

5.模型 Fit

    # GSU 长期序列行为训练
    GSU_model.fit([history, candidate], labels, epochs=10, batch_size=128)

示例样本，fit 只是走通流程，metric 不做参考：

 

五.Soft Search 软搜索

为了进一步加快万长度用户行为 Top-K 搜索速度，基于嵌入向量 E，论文中采用亚线性时间最大内积搜索方法 ALSH，搜索与目标项相关的 Top-K 行为。之前论文中还介绍过局部敏感 Hash 分桶的快速缓存搜索方法，这里示例使用最大堆 Heap 实现简易 Maximum Inner Product 的 Top-K 方法。

1.获取 Embedding 参数

kernel = np.array(GSU_model.get_layer("GSU").get_weights()[0])

kernel 即为商品的嵌入层，其维度为 N x embedding_dim，本例中 Kernel Size = (1000000, 8)。
 

2.Soft Search

通过 heapq.nlargers 实现 Top-K Good 的排序，然后基于 Top-K Good 的 Index 索引构建 SBS 用户长期行为子序列，送到后面的 ESU 通过 Attention 机制进行精确搜索。

class SoftSearch:

    def __init__(self, _kernel, _K):
        self.kernel = _kernel
        self.K = _K
        print("Kernel Size:", kernel.shape)

    def genTopK(self, good_history, target):

        _topKGoods = []
        _topKScores = []

        for sample in zip(good_history, target):
            score = []
            cur_seq, cur_tar = sample
            cur_tar_emd = np.squeeze(kernel[cur_tar])
            for seq in cur_seq:
                score.append(np.dot(kernel[seq], cur_tar_emd))
            # 获取下标
            topKIndex = heapq.nlargest(self.K, range(len(score)), score.__getitem__)
            # 获取数值
            topKScore = heapq.nlargest(self.K, score)

            _topKGoods.append(topKIndex)
            _topKScores.append(topKScore)

        return _topKGoods, _topKScores

3.Soft Search 取 Top-K 

论文中 Top-K 的 K 取 200 送入 GSU，这里示例取 10 跑通 Demo。 

    K = 10
    search = SoftSearch(kernel, K)
    topKGoods, topKScores = search.genTopK(history, candidate)

    for SBS, Score in zip(topKGoods, topKScores):
        print(SBS, Score)

其中 SBS 的长度为 K，后面的 Scores 是内积后排序的依据，这里是从大到小取 Top。 

 

六.总结

至此，简易的 GUS with Soft Search 就实现了，论文中由于软搜索与硬搜索得到的 SBS 序列相近且大部分为对应 Item 的同 Cate 类型商品，在权衡性能收益与资源消耗后，阿里巴巴选择使用 Hard Search 即 KKV 的形式进行 GSU 的通用搜索，但是这不妨碍 Soft Search 可以作为一种 Embedding 预训练的方式挖掘长期商品对应的向量。

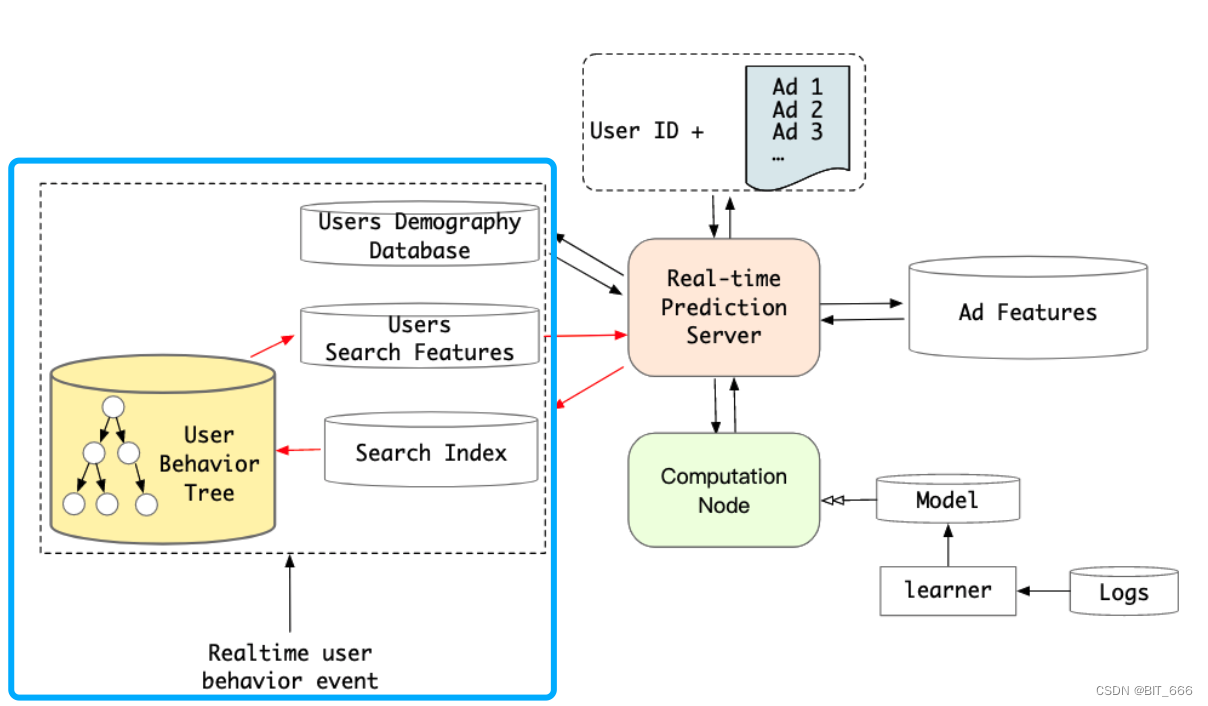
工程上阿里巴巴采用 Tree 的形式构造 KKV 存储结构。