🍎 博客主页:🌙@披星戴月的贾维斯
🍎 欢迎关注:👍点赞🍃收藏🔥留言
🍇系列专栏:🌙 C/C++专栏
🌙请不要相信胜利就像山坡上的蒲公英一样唾手可得,但是请相信,世界上总有一些美好值得我们全力以赴,哪怕粉身碎骨!🌙
🍉一起加油,去追寻、去成为更好的自己!

文章目录
- 前言
- 🍎1、A-画牌河
- 🍎2、不点两面(easy version)
- 🍎3、开题顺序
- 🍎4、算法模板总结- 来源:acwing
- 整数二分算法模板
- 浮点数二分算法模板
- 一维前缀和
- 二维前缀和
- 一维差分
- 二维差分
- 双指针算法
- 单链表
- 模拟栈
- 模拟队列
- 单调栈
- 单调队列 -常用于解决滑动窗口问题
- 并查集
- C++ STL简介
- 🍎5、总结
提示:以下是本篇文章正文内容,下面案例可供参考
前言
蓝桥杯在悄无声息中就来了,我上次参加就仅仅只拿了一个省三,期待通过自己的努力,能够更进一步,也希望在这和大家分享的竞赛题和模板你们能用得上。一起加油!
🍎1、A-画牌河
🔥1.1题目链接 画牌河
来源:牛客小白月赛67A题
🔥1.2题目描述
x魂是一款深受acmer喜爱的立直麻将游戏,在x魂中,玩家打的牌会放入牌河中,牌河是一个33行66列的区域,牌先放到第一行,放满后再在下一行放,同一行的牌是从左往右依次放的。
输入一个x,请你画出放置了x张牌的牌河。
输入描述
输入一个整数 x(0≤x≤18),表示放置的牌数。
输出描述:
输出一个3行6列的区域,每个位置为1表示放置了一张牌,为0表示为空。
示例1:
输入
8
输出
111111
110000
000000
🔥1.3分析题意
A题,简单模拟即可,就是把矩阵n位置成1,只要一个for循环暴力。
🔥1.4C++代码示例
#include<bits/stdc++.h>
using namespace std;
int a[4][20];
int n;
int main ()
{
cin >> n;
for(int i = 0; i < 3; i++)
{
for(int j = 0; j < 6; j++)
{
if(n > 0)
{
a[i][j] = 1;
n --;
}
}
}
for(int i = 0; i < 3; i ++)
{
for(int j = 0; j < 6; j++)
{
cout << a[i][j];
}
cout << endl;
}
return 0;
}
🍎2、不点两面(easy version)
🔥2.1题目链接🔥不点两面(easy version)
🔥2.2题目描述🔥
x魂是一款深受acmer喜爱的立直麻将游戏,在x魂中,认为不点两面听牌的牌是比较安全的,本题需要你求出在只有万子的x魂中,有几种牌是比较安全的。
具体来说,每张牌上有一个数字,数字范围在1到m之间。场上还有一个对手的牌河,对手的牌河中有若干张对手已经打出的牌。定义比较安全牌为:该牌上写有的数字x满足x−3或x+3至少在对手牌河里出现过一次。
请你求出,在m种牌中有几种牌是比较安全的。
对手的牌河初始为空,对手会不断向牌河中加入或移出一张牌共q次,你需要在每次对手操作后都给出当前状况下的答案。
输入描述:
输入第一行是两个整数m,q(1≤m≤100,1≤q≤200),含义如题目所述。
接下来qq行,每行输入两个整数op,num(1≤op≤2,1≤num≤m),表示一次操作,具体来说:
op=1表示对手向牌河中加入了一张num;
op=2表示对手从牌河中移出了一张num,保证移出的牌操作前一定在牌河里有至少一张。
注意牌河中可能有写有相同数字的牌出现多次。
输出描述
输出q行,第i行表示第i次操作后,m种牌中有几种牌是比较安全的。
示例1:
输入:
10 5
1 4
1 10
1 4
2 4
2 4
输出
2
2
2
2
1
🔥2.3分析题意
根据题意,我们要在1 - m中找到符合 i + 3 或者 i - 3 == x, x是牌河中有的数, 而且牌河中的数可能会重复, 因此我们要想一种数据类型既可以方便我们插入删除,又能查找比较方便,而且数据大小还是可以接受的q <= 200,针对查找vector数组中是否有num这个元素,可以用count接口来实现.
🔥2.4C++代码示例
#include<bits/stdc++.h>
using namespace std;
int m, q;
vector<int> ph;
bool st[200];
int main ()
{
cin >> m >> q;
while(q --)
{
memset(st, 0, sizeof st);//每次我们重置st 数组
int op, num;
int res = 0;
cin >> op >> num;
if(op == 1)
{
ph.push_back(num);
}
else
{
auto it = ph.begin();
while(it != ph.end())
{
if(*it == num) break;
else ++it;
}
ph.erase(it);
}
for(int i = 1; i <= m; i++)
{
int h = i + 3, f = i - 3;
if(count(ph.begin(), ph.end(), h) && st[i] == false)
{
res++;
st[i] = true;
}
if(count(ph.begin(), ph.end(), f) && st[i] == false)
{
res++;
st[i] = true;
}
}
cout << res << endl;
}
return 0;
}
我看了别人的题解发现了一种更好的做法,直接用数组操作,简单,速度又快
链接
题意:在1到m的数字中满足 x-3或x+3 在 牌河中出现的数字个数
题解:定义一个数组a[N],来统计数字x出现的次数。定义sum表示不重复数字的个数。
每往牌河中添加一个数字,a[x-3]++ , a[x+3]++。如果a[x-3]==0,那么sum++;a[x+3]同理。
每在牌河中删除一个数组,a[x-3]-- , a[x+3]–。如果a[x-3]==0,那么sum–;a[x+3]同理。
代码示例:
#include <iostream>
#include <algorithm>
#include <cstring>
#include <vector>
#include <queue>
#include <math.h>
#include <string>
#include <set>
#define PI 3.14159
using namespace std;
typedef pair<int,int> PII;
typedef long long LL;
const int MAX_INT = 0x3f3f3f3f;
const int N = 1e5+15;
const int mod = 1e9+7;
int a[N];
void solve()
{
int m,q;
cin>>m>>q;
int sum = 0;
while(q--)
{
int op,num;
cin>>op>>num;
if(op==1)
{
int x = num - 3;
int y = num + 3;
if(x>=1)
{
if(a[x]==0)sum++;
a[x]++;
}
if(y<=m)
{
if(a[y]==0)sum++;
a[y]++;
}
}
else
{
int x = num - 3;
int y = num + 3;
if(x>=1)
{
a[x]--;
if(a[x]==0)sum--;
}
if(y<=m)
{
a[y]--;
if(a[y]==0)sum--;
}
}
cout<<sum<<endl;
}
}
int main()
{
ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);
int T = 1;
while(T--)
{
solve();
}
}
🍎3、开题顺序
🔥3.1题目链接 开题顺序
由于这一题用到的算法是暴力求全排列+枚举,我们可以先去看acwing 递归求全排列的模板题,看完这题,做开题顺序就比较简单,而且容易理解。
递归实现排列型枚举
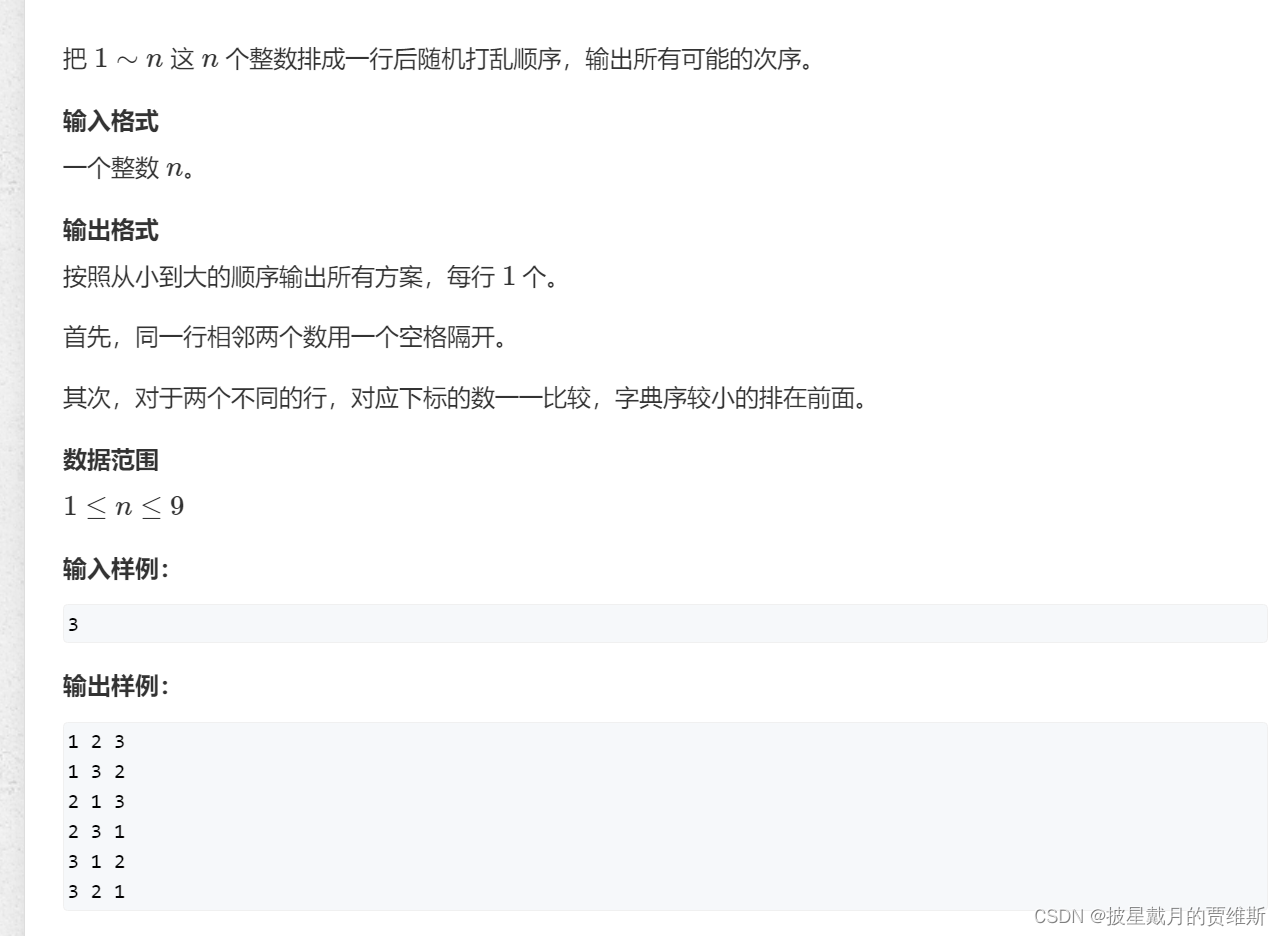
#include<bits/stdc++.h>
using namespace std;
const int N = 12;
int a[N];
bool st[N]; //判断这个值是不是被用过
int n;
void dfs(int u)
{
if(u >= n)
{
for(int i = 0; i < u; i++)
{
cout << a[i] << " ";
}
cout << endl;
return;
}
for(int i = 1; i <= n; i++)
{
if(!st[i])
{
st[i] = true;
a[u] = i;
dfs(u + 1);
st[i] = false;//恢复现场
}
}
}
int main ()
{
cin >> n;
dfs(0);//从第0个数和0状态开始搜索
return 0;
}
**题目描述 **
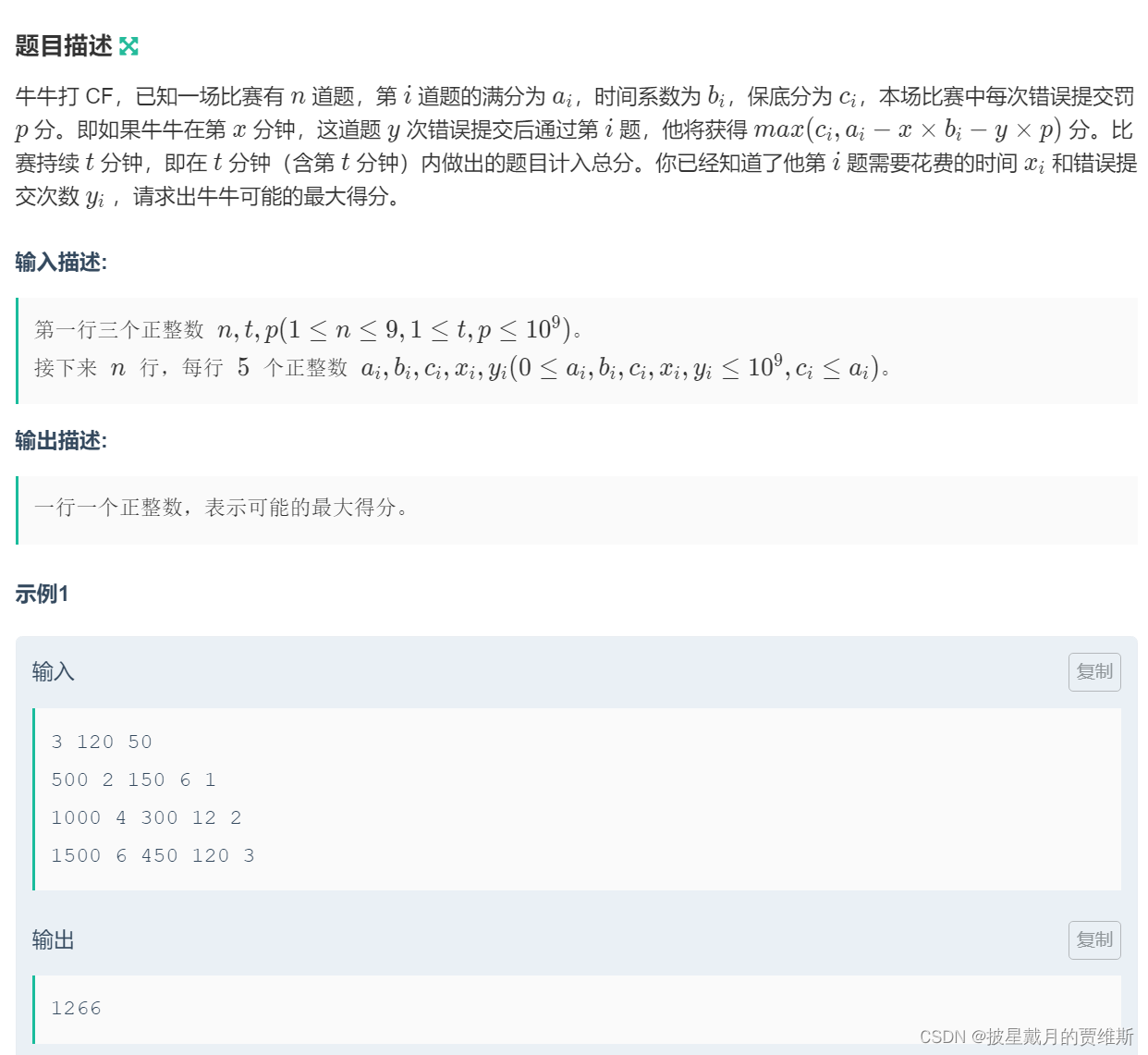

🔥3.3分析题意
看数据范围1 <= n <= 9,我们就知道这题可以用dfs过,这道题的分数大小会和做题有关,所以我们要枚举所有的开题可能,即递归枚举全排列,代码如下。
🔥3.4代码示例
#include<bits/stdc++.h>
using namespace std;
typedef long long LL;
int n, t, p;
const int N = 12;
int tmp[N];
bool st[N];
LL ans;
LL a[N], b[N], c[N], x[N], y[N];
//枚举全排列
void dfs(int u, int T)
{
if(u >= n || T >= t )
{
LL res =0, ti = 0;
for(int i = 0; i < u; i++)
{
auto &idx = tmp[i];
ti += x[idx];
if(ti <= t) res += max(c[idx], a[idx] - ti * b[idx] - y[idx] * p);
else break;
}
ans = max(ans, res);
return;
}
for(int i = 1; i <= n; i++)
{
if(!st[i])
{
st[i] = true;
tmp[u] = i;
dfs(u + 1, T + x[i]);
st[i] = false;
}
}
}
int main()
{
cin >> n >> t >> p;
for(int i = 1; i <= n; i++)
{
cin >> a[i] >> b[i] >> c[i] >> x[i] >> y[i];
}
dfs(0, 0);
cout << ans << endl;
return 0;
}
🍎4、算法模板总结- 来源:acwing
整数二分算法模板
bool check(int x) {/* ... */} // 检查x是否满足某种性质
// 区间[l, r]被划分成[l, mid]和[mid + 1, r]时使用:
int bsearch_1(int l, int r)
{
while (l < r)
{
int mid = l + r >> 1;
if (check(mid)) r = mid; // check()判断mid是否满足性质
else l = mid + 1;
}
return l;
}
// 区间[l, r]被划分成[l, mid - 1]和[mid, r]时使用:
int bsearch_2(int l, int r)
{
while (l < r)
{
int mid = l + r + 1 >> 1;
if (check(mid)) l = mid;
else r = mid - 1;
}
return l;
}
浮点数二分算法模板
bool check(double x) {/* ... */} // 检查x是否满足某种性质
double bsearch_3(double l, double r)
{
const double eps = 1e-6; // eps 表示精度,取决于题目对精度的要求
while (r - l > eps)
{
double mid = (l + r) / 2;
if (check(mid)) r = mid;
else l = mid;
}
return l;
}
一维前缀和
S[i] = a[1] + a[2] + ... a[i]
a[l] + ... + a[r] = S[r] - S[l - 1]
二维前缀和
S[i, j] = 第i行j列格子左上部分所有元素的和
s[i][j] = s[i - 1][j] + s[i][j - 1] - s[i - 1][j - 1] + a[i][j];
以(x1, y1)为左上角,(x2, y2)为右下角的子矩阵的和为:
S[x2, y2] - S[x1 - 1, y2] - S[x2, y1 - 1] + S[x1 - 1, y1 - 1]
一维差分
给区间[l, r]中的每个数加上c:B[l] += c, B[r + 1] -= c
二维差分
void add(int x1, int y1, int x2, int y2, int c)
{
b[x1][y1] += c;
b[x1][y2 + 1] -= c;
b[x2 + 1][y1] -= c;
b[x2 + 1][y2 + 1] += c;
}
a[i][j] = a[i - 1][j] + a[i][j - 1] - a[i - 1][j - 1] + b[i][j];//这里使用二维前缀和公式
双指针算法
for (int i = 0, j = 0; i < n; i ++ )
{
while (j < i && check(i, j)) j ++ ;
// 具体问题的逻辑
}
常见问题分类:
(1) 对于一个序列,用两个指针维护一段区间
(2) 对于两个序列,维护某种次序,比如归并排序中合并两个有序序列的操作
单链表
// head存储链表头,e[]存储节点的值,ne[]存储节点的next指针,idx表示当前用到了哪个节点
int head, e[N], ne[N], idx;
// 初始化
void init()
{
head = -1;
idx = 0;
}
// 在链表头插入一个数a
void insert(int a)
{
e[idx] = a, ne[idx] = head, head = idx ++ ;
}
// 将头结点删除,需要保证头结点存在
void remove()
{
head = ne[head];
}
模拟栈
// tt表示栈顶
int stk[N], tt = 0;
// 向栈顶插入一个数
stk[ ++ tt] = x;
// 从栈顶弹出一个数
tt -- ;
// 栈顶的值
stk[tt];
// 判断栈是否为空,如果 tt > 0,则表示不为空
if (tt > 0)
{
}
模拟队列
// hh 表示队头,tt表示队尾
int q[N], hh = 0, tt = -1;
// 向队尾插入一个数
q[ ++ tt] = x;
// 从队头弹出一个数
hh ++ ;
// 队头的值
q[hh];
// 判断队列是否为空,如果 hh <= tt,则表示不为空
if (hh <= tt)
{
}
单调栈
常见模型:找出每个数左边离它最近的比它大/小的数
int tt = 0;
for (int i = 1; i <= n; i ++ )
{
while (tt && check(stk[tt], i)) tt -- ;
stk[ ++ tt] = i; //元素入队列
}
单调队列 -常用于解决滑动窗口问题
常见模型:找出滑动窗口中的最大值/最小值
int hh = 0, tt = -1;
for (int i = 0; i < n; i ++ )
{
while (hh <= tt && check_out(q[hh])) hh ++ ; // 判断队头是否滑出窗口
while (hh <= tt && check(q[tt], i)) tt -- ;
q[ ++ tt] = i;
}
并查集
(1)朴素并查集:
int p[N]; //存储每个点的祖宗节点
// 返回x的祖宗节点
int find(int x)
{
if (p[x] != x) p[x] = find(p[x]);
return p[x];
}
// 初始化,假定节点编号是1~n
for (int i = 1; i <= n; i ++ ) p[i] = i;
// 合并a和b所在的两个集合:
p[find(a)] = find(b);
(2)维护size的并查集:
int p[N], size[N];
//p[]存储每个点的祖宗节点, size[]只有祖宗节点的有意义,表示祖宗节点所在集合中的点的数量
// 返回x的祖宗节点
int find(int x)
{
if (p[x] != x) p[x] = find(p[x]);
return p[x];
}
// 初始化,假定节点编号是1~n
for (int i = 1; i <= n; i ++ )
{
p[i] = i;
size[i] = 1;
}
// 合并a和b所在的两个集合:
size[find(b)] += size[find(a)];
p[find(a)] = find(b);
(3)维护到祖宗节点距离的并查集:
int p[N], d[N];
//p[]存储每个点的祖宗节点, d[x]存储x到p[x]的距离
// 返回x的祖宗节点
int find(int x)
{
if (p[x] != x)
{
int u = find(p[x]);
d[x] += d[p[x]];
p[x] = u;
}
return p[x];
}
// 初始化,假定节点编号是1~n
for (int i = 1; i <= n; i ++ )
{
p[i] = i;
d[i] = 0;
}
// 合并a和b所在的两个集合:
p[find(a)] = find(b);
d[find(a)] = distance; // 根据具体问题,初始化find(a)的偏移量
C++ STL简介
vector, 变长数组,倍增的思想
size() 返回元素个数
empty() 返回是否为空
clear() 清空
front()/back()
push_back()/pop_back()
begin()/end()
[]
支持比较运算,按字典序
pair<int, int>
first, 第一个元素
second, 第二个元素
支持比较运算,以first为第一关键字,以second为第二关键字(字典序)
string,字符串
size()/length() 返回字符串长度
empty()
clear()
substr(起始下标,(子串长度)) 返回子串
c_str() 返回字符串所在字符数组的起始地址
queue, 队列
size()
empty()
push() 向队尾插入一个元素
front() 返回队头元素
back() 返回队尾元素
pop() 弹出队头元素
priority_queue, 优先队列,默认是大根堆
size()
empty()
push() 插入一个元素
top() 返回堆顶元素
pop() 弹出堆顶元素
定义成小根堆的方式:priority_queue<int, vector<int>, greater<int>> q;
stack, 栈
size()
empty()
push() 向栈顶插入一个元素
top() 返回栈顶元素
pop() 弹出栈顶元素
deque, 双端队列
size()
empty()
clear()
front()/back()
push_back()/pop_back()
push_front()/pop_front()
begin()/end()
[]
set, map, multiset, multimap, 基于平衡二叉树(红黑树),动态维护有序序列
size()
empty()
clear()
begin()/end()
++, -- 返回前驱和后继,时间复杂度 O(logn)
set/multiset
insert() 插入一个数
find() 查找一个数
count() 返回某一个数的个数
erase()
(1) 输入是一个数x,删除所有x O(k + logn)
(2) 输入一个迭代器,删除这个迭代器
lower_bound()/upper_bound()
lower_bound(x) 返回大于等于x的最小的数的迭代器
upper_bound(x) 返回大于x的最小的数的迭代器
map/multimap
insert() 插入的数是一个pair
erase() 输入的参数是pair或者迭代器
find()
[] 注意multimap不支持此操作。 时间复杂度是 O(logn)
lower_bound()/upper_bound()
unordered_set, unordered_map, unordered_multiset, unordered_multimap, 哈希表
和上面类似,增删改查的时间复杂度是 O(1)
不支持 lower_bound()/upper_bound(), 迭代器的++,--
bitset, 圧位
bitset<10000> s;
~, &, |, ^
>>, <<
==, !=
[]
count() 返回有多少个1
any() 判断是否至少有一个1
none() 判断是否全为0
set() 把所有位置成1
set(k, v) 将第k位变成v
reset() 把所有位变成0
flip() 等价于~
flip(k) 把第k位取反
🍎5、总结
本文和大家分享了几道牛客小白月赛的题解,以及一些实用的算法模板,希望对大家的蓝桥杯备战有所帮助,最后祝大家都能取得满意的成绩!