文章目录

1. 搜索旋转排序数组【中等】
- 1.1 题目描述
- 1.2 解题思路
- 1.3 代码实现
2. 有效的括号【简单】
- 2.1 题目描述
- 2.2 解题思路
- 2.3 代码实现
3. 买卖股票的最佳时机【简单】
- 3.1 题目描述
- 3.2 解题思路
- 3.3 代码实现
4. 环形链表【简单】
- 4.1 题目描述
- 4.2 解题思路
- 4.3 代码实现
5. 岛屿数量【中等】
- 5.1 题目描述
- 5.2 解题思路
- 5.3 代码实现

1. 搜索旋转排序数组【中等】

题目链接：https://leetcode.cn/problems/search-in-rotated-sorted-array/
参考题解：https://leetcode.cn/problems/search-in-rotated-sorted-array/solution/sou-suo-xuan-zhuan-pai-xu-shu-zu-by-leetcode-solut/

1.1 题目描述

整数数组 nums 按升序排列，数组中的值 互不相同 。

在传递给函数之前，nums 在预先未知的某个下标 k（0 <= k < nums.length）上进行了旋转，使数组变为 [nums[k], nums[k+1], …, nums[n-1], nums[0], nums[1], …, nums[k-1]]（下标 从 0 开始 计数）。例如， [0,1,2,4,5,6,7] 在下标 3 处经旋转后可能变为 [4,5,6,7,0,1,2] 。

给你 旋转后 的数组 nums 和一个整数 target ，如果 nums 中存在这个目标值 target ，则返回它的下标，否则返回 -1 。

你必须设计一个时间复杂度为 O(log n) 的算法解决此问题。

示例1：

输入：nums = [4,5,6,7,0,1,2], target = 0
输出：4

示例2：

输入：nums = [4,5,6,7,0,1,2], target = 3
输出：-1

示例3：

输入：nums = [1], target = 0
输出：-1

提示：

1 <= nums.length <= 5000
-10^4 <= nums[i] <= 10^4
nums 中的每个值都 独一无二
题目数据保证 nums 在预先未知的某个下标上进行了旋转
-10^4 <= target <= 10^4

1.2 解题思路

要达到题目要求的时间复杂度，肯定得考虑二分法。如果是一般的有序数组，直接二分很容易实现搜索。把数组旋转过后，得到的数组从中间分开，一定会有一半是有序的，满足最左边的元素小于最右边的元素，而另一半无序数组一定不满足这个条件（可以脑补一下）。所以在处理题目给出的数组时，可以在有序的那一半进行搜索，根据目标值是否在这个有序区间来更新左右边界。

1.3 代码实现

class Solution {
public:
    int search(vector<int>& nums, int target) {
        int len = nums.size();
        if(len == 1)
            return nums[0] == target ? 0 : -1;
        int left = 0, right = len - 1;
        while(left <= right) {
            int mid = (left + right) / 2;
            if(nums[mid] == target)
                return mid;
            if(nums[left] <= nums[mid]) {
                if(nums[left] <= target && target < nums[mid])
                    right = mid - 1;
                else
                    left = mid + 1;
            }
            else {
                if(nums[mid] < target && target <= nums[right])
                    left = mid + 1;
                else
                    right = mid - 1;
            }
        }
        return -1;
    }
};

2. 有效的括号【简单】

题目链接：https://leetcode.cn/problems/valid-parentheses/
参考题解：https://leetcode.cn/problems/valid-parentheses/solution/you-xiao-de-gua-hao-by-leetcode-solution/

2.1 题目描述

给定一个只包括 ‘(’，‘)’，‘{’，‘}’，‘[’，‘]’ 的字符串 s ，判断字符串是否有效。

有效字符串需满足：

左括号必须用相同类型的右括号闭合。
左括号必须以正确的顺序闭合。
每个右括号都有一个对应的相同类型的左括号。

示例1：

输入：s = “()”
输出：true

示例2：

输入：s = “()[]{}”
输出：true

示例3：

输入：s = “(]”
输出：false

提示：

1 <= s.length <= 10^4
s 仅由括号 ‘()[]{}’ 组成

2.2 解题思路

对于括号匹配问题，首先考虑用先进后出的堆来实现。每遇到一个左括号，就把它 push 入堆；每遇到一个右括号，就与堆顶的左括号比对看是否匹配。如果不匹配，或者字符串扫完后堆非空（有多余的左括号），则返回无效，否则返回有效。

2.3 代码实现

class Solution {
public:
    bool isValid(string s) {
        unordered_map<char, char> pairs = {
            {')', '('},
            {'}', '{'},
            {']', '['}
        };
        stack<char> lefts;
        for(int i = 0; i < s.length(); ++i) {
            if(!pairs.count(s[i]))
                lefts.push(s[i]);
            else {
                if(lefts.empty() || pairs[s[i]] != lefts.top())
                    return false;
                lefts.pop();
            }
        }
        if(lefts.empty())
            return true;
        else
            return false;
    }
};

3. 买卖股票的最佳时机【简单】

题目链接：https://leetcode.cn/problems/best-time-to-buy-and-sell-stock/
参考题解：https://leetcode.cn/problems/best-time-to-buy-and-sell-stock/solution/121-mai-mai-gu-piao-de-zui-jia-shi-ji-by-leetcode-/

3.1 题目描述

给定一个数组 prices ，它的第 i 个元素 prices[i] 表示一支给定股票第 i 天的价格。

你只能选择 某一天 买入这只股票，并选择在 未来的某一个不同的日子 卖出该股票。设计一个算法来计算你所能获取的最大利润。

返回你可以从这笔交易中获取的最大利润。如果你不能获取任何利润，返回 0 。

示例1：

输入：[7,1,5,3,6,4]
输出：5
解释：在第 2 天（股票价格 = 1）的时候买入，在第 5 天（股票价格 = 6）的时候卖出，最大利润 = 6-1 = 5 。
注意利润不能是 7-1 = 6, 因为卖出价格需要大于买入价格；同时，你不能在买入前卖出股票。

示例2：

输入：prices = [7,6,4,3,1]
输出：0
解释：在这种情况下, 没有交易完成, 所以最大利润为 0。

提示：

1 <= prices.length <= 10^5
0 <= prices[i] <= 10^4

3.2 解题思路

对于每一天的价格，如果是历史最低价，则把它记录下来，否则就将其与此前历史最低价算利润差，看是不是比截止到这天记录过的最大利润还要高。为什么可以这样做？因为如果这一天不是历史最低价，即便后面的股票价格再高，与这天的利润差也不可能会比与之前的历史最低价利润差更高。注意这里每次参考的历史最低价都是只考虑了这一天及之前出现过的价格，而不是全局的最低价。

3.3 代码实现

class Solution {
public:
    int maxProfit(vector<int>& prices) {
        int ans = 0;
        int min_price = prices[0];
        for(int i = 0; i < prices.size(); ++i) {
            if(prices[i] < min_price)
                min_price = prices[i];
            else if(prices[i] - min_price > ans)
                ans = prices[i] - min_price;
        }
        return ans;
    }
};

4. 环形链表【简单】

题目链接：https://leetcode.cn/problems/linked-list-cycle/
参考题解：https://leetcode.cn/problems/linked-list-cycle/solution/huan-xing-lian-biao-by-leetcode-solution/

4.1 题目描述

给你一个链表的头节点 head ，判断链表中是否有环。

如果链表中有某个节点，可以通过连续跟踪 next 指针再次到达，则链表中存在环。为了表示给定链表中的环，评测系统内部使用整数 pos 来表示链表尾连接到链表中的位置（索引从 0 开始）。注意：pos 不作为参数进行传递 。仅仅是为了标识链表的实际情况。

如果链表中存在环 ，则返回 true 。否则，返回 false 。

示例1：
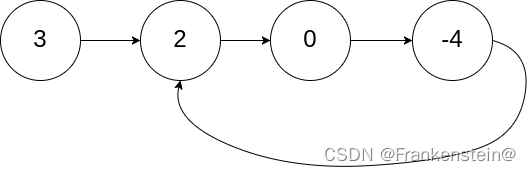
在这里插入图片描述

输入：head = [3,2,0,-4], pos = 1
输出：true
解释：链表中有一个环，其尾部连接到第二个节点。

示例2：
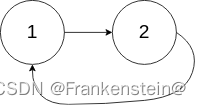
在这里插入图片描述

输入：head = [1,2], pos = 0
输出：true
解释：链表中有一个环，其尾部连接到第一个节点。

示例3：
在这里插入图片描述

输入：head = [1], pos = -1
输出：false
解释：链表中没有环。

提示：

链表中节点的数目范围是 [0, 10^4]
-10^5 <= Node.val <= 10^5
pos 为 -1 或者链表中的一个 有效索引 。

4.2 解题思路

最简单的方法就是用哈希表，把遍历过的节点都存下来，判断是否有重复访问的节点，但是这样会引入额外的空间开销。另一种方法是使用快慢指针，快指针每次移动两下，慢指针每次只移动一下，如果存在环的话，这两个指针会在某个时刻指向同一个节点。注意fast和slow开始时不能同时指向head，因为循环体中是先判断fast和slow是否重合，再往后移动，一开始都指向head的话循环体内第一个if判断完就直接返回了。此外边界情况要考虑周全。

4.3 代码实现

/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode(int x) : val(x), next(NULL) {}
 * };
 */
class Solution {
public:
    bool hasCycle(ListNode *head) {
        if(head == nullptr || head->next == nullptr) {
            return false;
        }
        ListNode *fast = head->next;
        ListNode *slow = head;
        while(fast->next != nullptr && fast->next->next != nullptr) {
            if(fast == slow)
                return true;
            fast = fast->next->next;
            slow = slow->next;
        }
        return false;
    }
};

5. 岛屿数量【中等】

题目链接：https://leetcode.cn/problems/number-of-islands/
参考题解：https://leetcode.cn/problems/number-of-islands/solution/dao-yu-shu-liang-by-leetcode/

5.1 题目描述

给你一个由 ‘1’（陆地）和 ‘0’（水）组成的的二维网格，请你计算网格中岛屿的数量。

岛屿总是被水包围，并且每座岛屿只能由水平方向和/或竖直方向上相邻的陆地连接形成。

此外，你可以假设该网格的四条边均被水包围。

示例1：

输入：grid = [
[“1”,“1”,“1”,“1”,“0”],
[“1”,“1”,“0”,“1”,“0”],
[“1”,“1”,“0”,“0”,“0”],
[“0”,“0”,“0”,“0”,“0”]
]
输出：1

示例2：

输入：grid = [
[“1”,“1”,“0”,“0”,“0”],
[“1”,“1”,“0”,“0”,“0”],
[“0”,“0”,“1”,“0”,“0”],
[“0”,“0”,“0”,“1”,“1”]
]
输出：3

提示：

m == grid.length
n == grid[i].length
1 <= m, n <= 300
grid[i][j] 的值为 ‘0’ 或 ‘1’

5.2 解题思路

扫描整个二维网格，如果某个位置是 1 ，则以其为起始节点开始进行深度优先搜索。在深度优先搜索的过程中，每个搜索到的 1 都会被重新标记为 0 ，这就表明该位置已经是属于当前搜索的岛屿的一部分了。只要是连通的部分，就会在一次深度搜索中被全部置 0 ，也就是形成了一个岛屿。把搜索过的位置标记为 0 是避免以其为起始节点再重复进行搜索。最终的岛屿数量就是进行深度优先搜索的次数。深度优先搜索可以用递归实现，每次往当前位置的上下左右节点进行递归搜索。

5.3 代码实现

class Solution {
public:
    void dfs(vector<vector<char>>& grid, int row, int col) {
        int num_rows = grid.size();
        int num_cols = grid[0].size();
        grid[row][col] = '0';
        if(row - 1 >= 0 && grid[row - 1][col] == '1')
            dfs(grid, row - 1, col);
        if(row + 1 < num_rows && grid[row + 1][col] == '1')
            dfs(grid, row + 1, col);
        if(col - 1 >= 0 && grid[row][col - 1] == '1')
            dfs(grid, row, col - 1);
        if(col + 1 < num_cols && grid[row][col + 1] == '1')
            dfs(grid, row, col + 1);
        return;
    }
    int numIslands(vector<vector<char>>& grid) {
        int ans = 0;
        int num_rows = grid.size();
        int num_cols = grid[0].size();
        if(!num_rows)
            return 0;
        for(int row = 0; row < num_rows; ++row) {
            for(int col = 0; col < num_cols; ++col) {
                if(grid[row][col] == '1') {
                    ++ans;
                    dfs(grid, row, col);
                }
            }
        }
        return ans;
    }
};