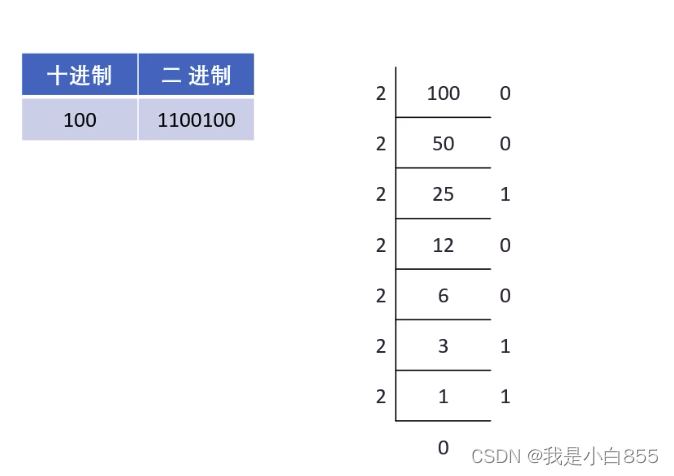
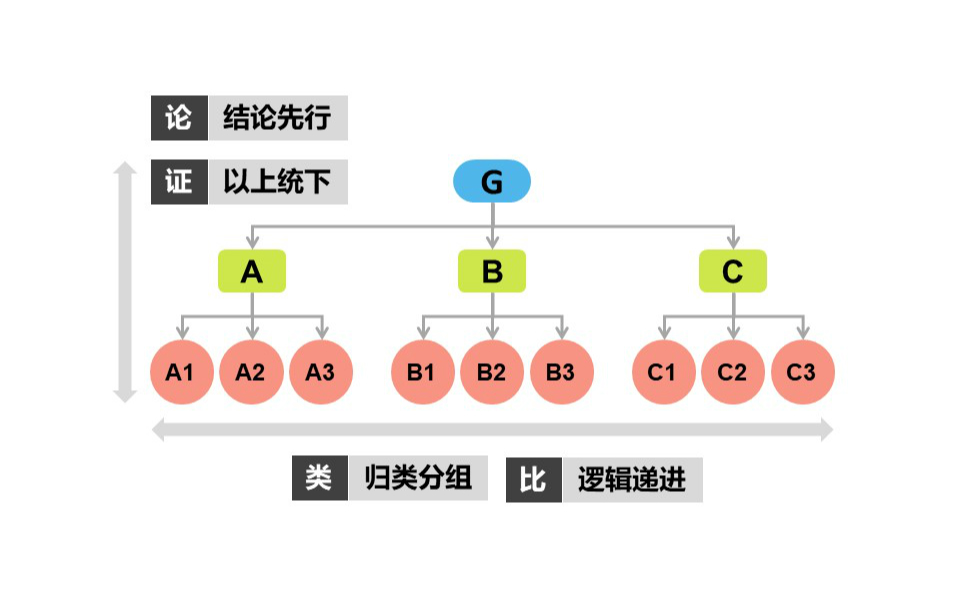
4.1

试证明对于不含冲突数据 (即特征向量完全相同但标记不同) 的训练集, 必存在与训练集一致 (即训练误差为 0)的决策树.

答案：

假设不存在与训练集一致的决策树，那么训练集训练得到的决策树至少有一个节点上存在无法划分的多个数据（若节点上没有冲突数据，那么总是能够将数据分开的）。这与前提-不含冲突数据 矛盾，因此必存在与训练集一致的决策树

解释：

解决这个问题需要先理解构建决策树过程中的2--7行：

输入：训练集D = {(x1, y1), (x2, y2), (x3, y3),..., (xm, ym)};
      属性集A = {a1, a2,..., ad}.
过程：函数TreeGenerate(D, A)

1: 生成结点node;
2: if D中样本全属于同一类别C then
3:       将node标记为C类叶节点; return;
4: end if
5: if A = NULL OR D中样本在A上取值相同 then
6:       将node标记为叶结点，令其类别标记为D中样本数最多的类; return;
7: end if
8: 从A中选择最优划分属性a*;
9: for a*中的每一个值a*v do
10:       为node生成一个分支，令Dv表示D中在a*上取值为a*v的样本子集；
11:       if Dv为空 then
12:             将分支结点标记为叶结点，其类别标记为D中样本最多的类； return；
13:       else
14:             以TreeGenerate(Dv, A\{a*})为分支结点
15:       end if
16: end for

决策树的生成是一个递归过程，有三种情形导致递归返回

1.当前结点所包含的样本都属于同一类别，无需划分

2: if D中样本全属于同一类别C then
3:       将node标记为C类叶节点; return;
4: end if

做法： 将当前结点标记为叶结点，并令该类别为结点的类别

这个很好理解，划分后的数据集的类别都是好瓜，那么再继续划分就没有意义了

2.所有样本在所有属性上取值相同，无法划分

5: if A = NULL then
6:       将node标记为叶结点，令其类别标记为D中样本数最多的类; return;
7: end if

做法：将当前结点标记为叶结点，但将其类别设定为父结点所含样本最多的类别（利用当前结点的后验分布）

这个不太好理解，意思是：西瓜A和西瓜B的所有属性一模一样，这俩西瓜都是色泽：浅白，敲声：沉闷，纹理：清晰。但是西瓜A是好瓜，西瓜B是坏瓜。比如有10个西瓜都是属性一模一样的，4好瓜，6坏瓜，那么这个结点就归类为坏瓜。

这种情况会导致验证训练集时存在误差，因为4个好瓜被归类为了坏瓜

这种情况即题干中的冲突数据 (即特征向量完全相同但标记不同)

3.当前结点包含的样本集合为空，不能划分

5: if D中样本在A上取值相同 then
6:       将node标记为叶结点，令其类别标记为D中样本数最多的类; return;
7: end if

做法：将当前结点标记为叶结点，但将其类别设定为父结点所含样本最多的类别（把父结点的样本分布作为当前结点的先验分布）

这个情况是这样的：假如我们划分到纹理时，一般情况数据集是既包含清晰和模糊这两种情况的

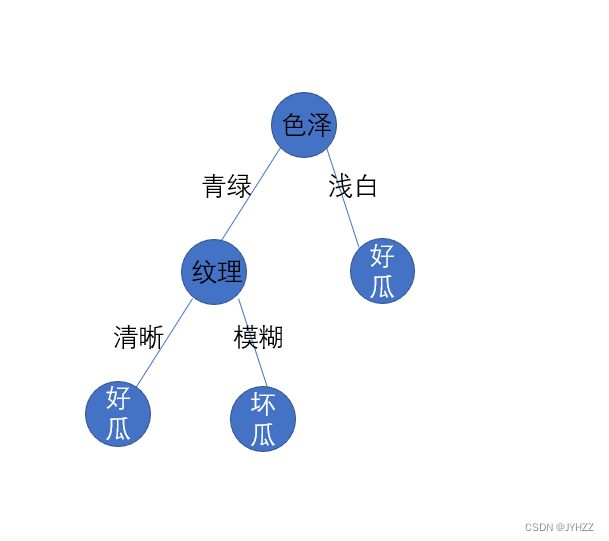
 但是，有时候存在只包含清晰这种情况，这时候我们就不能这样划分：

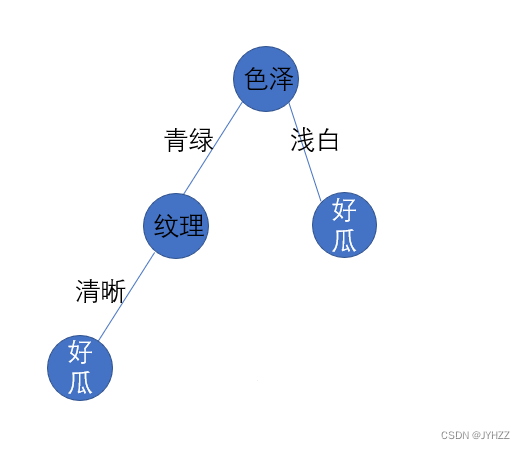
正确的做法是查看色泽为青绿的数据中，正例有多少，反例有多少，取最多的。 比如有10个西瓜是青绿的，4好瓜，6坏瓜，那么这个结点就归类为坏瓜。

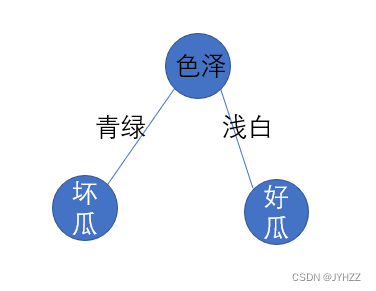
这种情况会导致验证训练集时存在误差

这种情况即题干中的冲突数据 (即特征向量完全相同但标记不同)

---

回到这道题，这道题是：

试证明对于不含冲突数据 (即特征向量完全相同但标记不同) 的训练集, 必存在与训练集一致 (即训练误差为 0)的决策树.

如果没有冲突数据，那么在运行中就不会执行

5: if A = NULL OR D中样本在A上取值相同 then
6:       将node标记为叶结点，令其类别标记为D中样本数最多的类; return;
7: end if

这样就不会产生误差，所以训练误差为0

题型：判断题

只要数据集不存在冲突。一棵决策树通常可以完美（100%）拟合训练数据。此时，这棵树的泛化误差也达到了最优值。T

4.2

试析使用 “最小训练误差” 作为决策树划分选择准则的缺陷.

答案：

若以最小训练误差作为决策树划分的依据，由于训练集和真是情况总是会存在一定偏差，这使得这样得到的决策树会存在过拟合的情况，对于未知的数据的泛化能力较差。因此最小训练误差不适合用来作为决策树划分的依据。

解释：

4.1的情况就是以最小训练误差作为决策树划分的依据，训练误差达到了0，但是现实情况中不是所有的西瓜都是这样的，这种做法导致了过拟合，对于未知的数据的泛化能力较差。

4.3
试编程实现基于信息熵进行划分选择的决策树算法, 并为表 4.3 4.34.3 中数据生成一棵决策树.

机器学习算法的Python实现 (2)：ID3决策树

《机器学习》西瓜书 第 4 章 编程实例

4.7
图 4.2是一种递归算法, 若面临巨量数据, 则决策树的层数会很深, 使用递归方法易导致 “栈” 溢出. 试使用 “队列” 数据结构, 以参数 MaxDepth控制树的最大深度, 写出与图 4.2等价、但不使用递归的决策树生成算法.

图4.2

输入：训练集D = {(x1, y1), (x2, y2), (x3, y3),..., (xm, ym)};
      属性集A = {a1, a2,..., ad}.
过程：函数TreeGenerate(D, A)

1: 生成结点node;
2: if D中样本全属于同一类别C then
3:       将node标记为C类叶节点; return;
4: end if
5: if A = NULL OR D中样本在A上取值相同 then
6:       将node标记为叶结点，令其类别标记为D中样本数最多的类; return;
7: end if
8: 从A中选择最优划分属性a*;
9: for a*中的每一个值a*v do
10:       为node生成一个分支，令Dv表示D中在a*上取值为a*v的样本子集；
11:       if Dv为空 then
12:             将分支结点标记为叶结点，其类别标记为D中样本最多的类； return；
13:       else
14:             以TreeGenerate(Dv, A\{a*})为分支结点
15:       end if
16: end for

算法：

# 输入: 训练集 D
#      属性集 A
array[0] = [D, A]
for D, A in array:
    生成节点node;
    if D中样本全属于同一类别C:
        将node标记为C类叶节点
        continue
    elif A = 空 or D中样本在A上取值相同:
        将node标记为叶节点, 其类别标记为D中样本数最多的类
        continue
    从A中选择最优划分属性a
    for a_v in a每个取值:
        为node生成一个分支, 令D_v表示D在a上取值为a_v的样本子集
        if D_v == null:
            将分支节点标记为叶节点, 其类别标记为D中样本最多的类
            continue
        elif
            array.append([D_v, A \ {a}])
# 输出: 以node为根节点的一棵决策树