一、数组

什么是数组？

数组：在内存中用一串连续的区域来存放一些值。数组是相同类型数据元素的有序集合

数组是由相同类型的元素的集合组成的数据结构

连续内存：JS的数组元素可以是任意类型，JS中的内存地址是不连续的

数组的优点：

1. 按照索引查询元素的时候速度很快
2. 存储大量的数据
3. 按照索引去遍历数组
4. 定义方便，访问很灵活

 

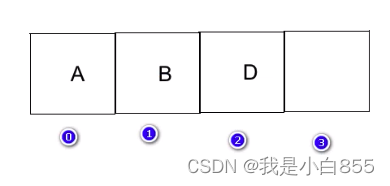
数组的缺点：

1. 根据内容查找会很慢-index
2. 数组的大小一经确定是不能改变的，不适合动态存储
3. 数组只能存储相同类型的数据
4. 增加、删除元素效率很低（尽量避免从头部插入）

清空数组有几种方法：

• length = 0
• = []
• splice()

 二、栈

内存区域：栈区

单片机：压栈

数据结构中，有一个同名的结构：栈。

内存中的堆栈和数据结构中的堆栈不是一个概念，内存中的堆栈是真实存在的物理区，数据结构中的堆栈式抽象数据存储结构

栈：是一种受限制的线性表。它遵循后进先出（LIFO）

栈的应用：十进制转二进制

 

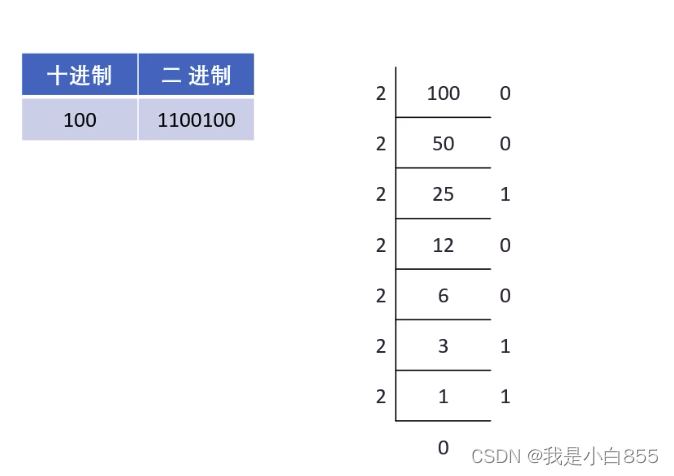
// 十进制转化二进制
const binary = （number）=>{
	let stack = new Stack();
	let remainder = 0;
	let top = '';
	
	while(number>0){
		remainder = number%2;
		stack.push(remainder);
		number = Math.floor(number/2);
	}
	while(!stack.isEmpty()){
		top+=stack.pop();
	}
	return top;
}

 最开始的时候，栈式不含有任何数据的，叫做空栈。

class Stack(){
	constructor(){
		this.items = [];
	}
	push(ele){
		this.items.push(ele);
	}
	pop(){
		return this.items.pop();
	}
	// 栈顶
	peek(){
		return this.items[this.item.length - 1]
	}
	// 判空
	isEmpty(){
		return this.items.length === 0 ;
	}
	// 长度
	size(){
		return this.items.length;
	}
	// 清空
	clear(){
		this.items.length = 0
	}
}

push()：数组末尾推入

pop()：数组末尾推出

javascript的调用栈（执行栈）

执行上下文：执行上下文就是当前JS代码被解析和执行所在环境的抽象的概念

JS中的任何代码都是在执行上下文中运行的。（执行环境）

JS的执行上下文分三种：全局执行上下文、函数执行上下文、Eval

• 全局执行上下文：默认的，它是最基础的执行上下文。

1. 创建全局对象
2. 将this指向这个全局对象
3. 执行js的时候就压入栈底，关闭浏览器的时候才弹出

• 函数执行上下文：每次调用函数的时候，会为这个函数创建一个新的执行上下文。

1. JS引擎创建一个新的全局执行上下文并且将这个执行上下文推入到当前的执行栈中（执行栈用于：存储在代码执行期间创建的所有的执行上下文）
2. 每当发生函数调用的时候，JS引擎都会为该函数创建一个新的执行上下文并且PUSH到当前执行栈的栈顶

• Eval函数执行上下文

 JS的执行上下文分两个阶段

• 创建阶段

1. 创建词法环境
2. 生成变量对象(VO)，建立作用域链、作用域链、作用域链（重要的事说三遍）；函数环境会创建变量对象：arguments对象（并赋值）、函数声明（并赋值）、变量声明（不赋值），函数表达式声明（不赋值）；会确定this指向；会确定作用域
3. 确认this指向，并绑定this

• 执行阶段。这个阶段进行变量赋值，函数引用及执行代码。变量赋值、函数表达式赋值，使变量对象编程活跃对象

递归的原理

函数的调用的本质：“压栈与出栈操作”。函数在在调用栈里边有一个特例，叫做递归

递归：自己调自己

递归调用，递归栈。LIFO

先进栈，到条件后再出栈，如果不出栈，就会导致：栈溢出

 阶乘：1到n到连续自然数相乘的积

 

const factor = (n)=>{
        if(n===1){
            return 1;
        }
     return n*factor(n-1);

    }

斐波那契数列：从第3项开始，每一项都等于前两项的和 

一般而言，兔子在出生两个月后，就有繁殖能力，一对兔子每个月能生出一对小兔子来。如果所有兔都不死，那么一年以后可以繁殖多少对兔子？

1,1,2,3,5,8,13...

F(1) = 1,F(2) = 1 ...

F(n) = F(n-1)+F(n-2)

const Fibonacci = (n) => {
  if (n <= 1) {
    return 1;
  }
  return Fibonacci(n - 1) + Fibonacci(n - 2);
};

尾调用优化以上两个算法：

//  把前面两位数，当作参数传进来
const Fibonacci = (n, ac1 = 1, ac2 = 1) => {
  if (n <= 1) {
    return ac2;
  }

  return Fibonacci(n - 1, ac2, ac1 + ac2);
};

/* 
重复计算的问题
n = 5 ,Fibonacci(4)+Fibonacci(3)
n = 4,Fibonacci(3)+Fibonacci(2)
...
递归需要同时保存成百上千个调用帧。很容易就会发生栈溢出
但是对于尾递归来说。由于只存在一个调用栈，所以永远不会发生栈溢出错误
Fibonacci(50)
*/

const factor = (n,total) =>{
  if (n === 1) {
    return total;
  }
  return factor(n-1, n * total)
}

// 初始值
console.log(factor(10,1));