说明

获取随机数大家应该都有用到过 Math.random() 这个函数，下面来看看源码的注释。

/**
     * Returns a {@code double} value with a positive sign, greater
     * than or equal to {@code 0.0} and less than {@code 1.0}.
     * Returned values are chosen pseudorandomly with (approximately)
     * uniform distribution from that range.
     *
     * <p>When this method is first called, it creates a single new
     * pseudorandom-number generator, exactly as if by the expression
     *
     * <blockquote>{@code new java.util.Random()}</blockquote>
     *
     * This new pseudorandom-number generator is used thereafter for
     * all calls to this method and is used nowhere else.
     *
     * <p>This method is properly synchronized to allow correct use by
     * more than one thread. However, if many threads need to generate
     * pseudorandom numbers at a great rate, it may reduce contention
     * for each thread to have its own pseudorandom-number generator.
     *
     * @return  a pseudorandom {@code double} greater than or equal
     * to {@code 0.0} and less than {@code 1.0}.
     * @see Random#nextDouble()
     */
    public static double random() {
        return RandomNumberGeneratorHolder.randomNumberGenerator.nextDouble();
    }

主要就是第一段注释说明如下：

返回 [0, 1) 之间的 double 类型的一个浮点数。
返回的值是以（近似）均匀分布的方式从该范围内伪随机选择的。

说实话，能做到等概率返回一个数，实际中是比较难做到的，但是在计算机中还是有办法做到的。所以厉害就厉害在这个 等概率返回某个数。

验证函数等概率返回功能

验证代码比较简单，如下：

		// 验证 random 函数的等概率返回功能
        int count = 0,testCount = 100000;
        for (int i  = 0;i < testCount;i++){
            if (Math.random() < 0.6){
                count++;
            }
        }
        System.out.println(":> count=" + count + ", 占比 " + (double)count / (double)testCount);

这里做了十万次获取随机数的操作。

如果每次返回的数小于 0.6 ，那么对变量 count 进行加 1 统计，循环十万次后最后得到 count 的值，然后用 count 除以总测试次数，得到实际占比。

如果实际占比也是 0.6 或者是无限接近 0.6 就说明验证函数等概率返回是成功的。

结果如下：

在这里插入图片描述

实际占比无限接近 0.6，故验证成功。

验证 [0, 8)上也是等概率返回一个数的功能

当 Math.random() * 8 后，是不是也是等概率返回 [0, 8) 中的一个浮点数，我们来继续验证。

验证代码如下：

		// 验证 [0, 8)上也是等概率返回一个数的功能
		int count = 0,testCount = 100000;
		for (int i = 0;i < testCount;i++){
            // 预期占比应该是 4/8
            if (Math.random() * 8 < 4){
                count++;
            }
        }
System.out.println(":> count=" + count + ", 占比 " + (double)count / (double)testCount);

这里也是进行十万次获取随机数操作。

每次获取的随机数乘以整数 8 ，如果该值小于 4 ，就对变量 count 进行加 1 统计，循环十万次后得到最终 count 的值，用该值除以总测试次数得到实际占比，如果跟预期占比 4/8 相同或者无限接近预期占比 4/8，就说明验证成功。

结果如下：

在这里插入图片描述

可以看到，实际占比很接近预期占比 4/8 ，故验证成功。

验证等概率返回[0, K - 1]中的一个整数

这里假定 K 是一个大于 2 的整数。

我们具体化一个例子进行验证。假设 K = 10，那么就是验证 Math.random() * 10 是不是等概率返回 [0, K - 1]中的一个整数。

验证代码如下：

		int count = 0,testCount = 100000;
		// 验证等概率返回[0, K - 1]中的一个整数
		int K = 10;
		int[] countK = new int[K];// countK[0] = 0出现的次数、countK[1] = 1出现的次数
		for (int i = 0;i < testCount;i++){
            int ranK = (int)(Math.random() * K);
            countK[ranK]++;
        }

		for (int i = 0;i < K;i++){
            System.out.println(":> " + i + " 出现的次数： " + countK[i]);
        }

进行十万次获取随机数操作。

创建一个整型数组 countK 保存每个整数（从 0 到 9）出现的次数。每次获取的随机数乘以 10，给该值取 int 整型，看得到的整数 ranK 是多少，就给 countK[ranK] 进行加 1 操作。

当循环十万次操作后，得到的 countK 数组中各个元素的值就是从 0 到 9 各个整数出现的次数。

如果 countK 数组中每个元素的值都无限接近或者相等，就说验证成功。

结果如下：

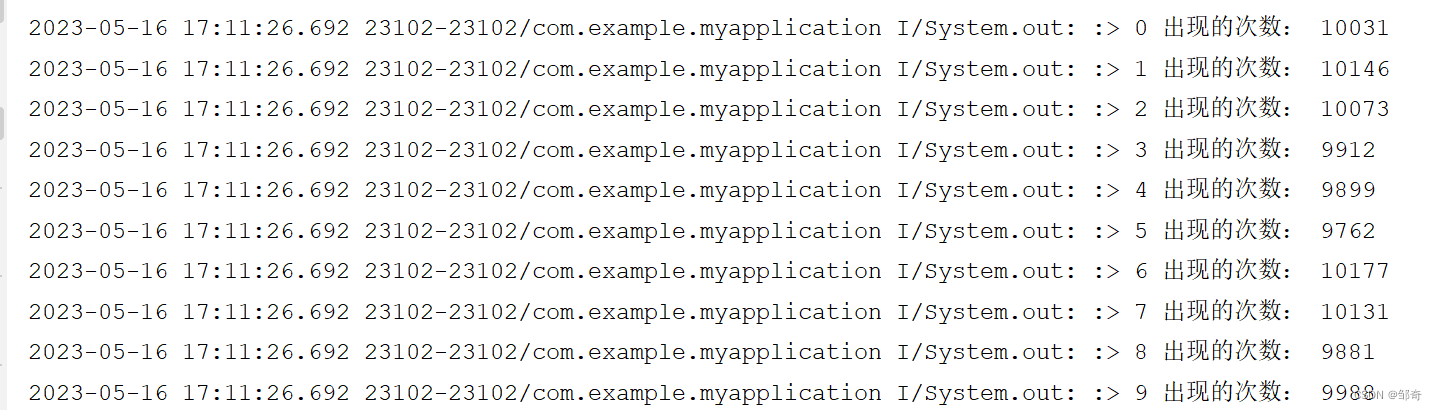
可以看到 10 以内的每个整数出现的次数可以认为基本相同，故验证成功。

实现：任意x，x属于[0, 1)，[0, x)范围上的数出现概率由原来的x调整成x平方

由上面几个验证可知，随机函数Math.random()返回的某个数 x，x ∈ [0, 1)，并且因为 x 是等概率返回的某个数，所以随机函数返回 [0, x)范围上的数出现的概率是 x。

验证代码如下：

		int count = 0,testCount = 100000;
		double x = 0.6;

		private double xPow2(){
        	// 注意这里取两个随机数中的最大值
        	return Math.max(Math.random(), Math.random());
    	}

		// 实现：任意x，x属于[0, 1)，[0, x)范围上的数出现概率由原来的x调整成x平方
        count = 0;
        double x = 0.6;
        Math.max(Math.random(), Math.random());
        for (int i = 0;i < testCount;i++){
            if (xPow2() < x){
                count++;
            }
        }
        System.out.println(":> 预期占比 " + Math.pow(x, 2));
        System.out.println(":> 实际占比 " + (double)count / (double)testCount);