62 . 不同路径

题目详情

一个机器人位于一个 m x n 网格的左上角（起始点在下图中标记为 “Start” ）。

机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角（在下图中标记为 “Finish” ）。

问总共有多少条不同的路径？

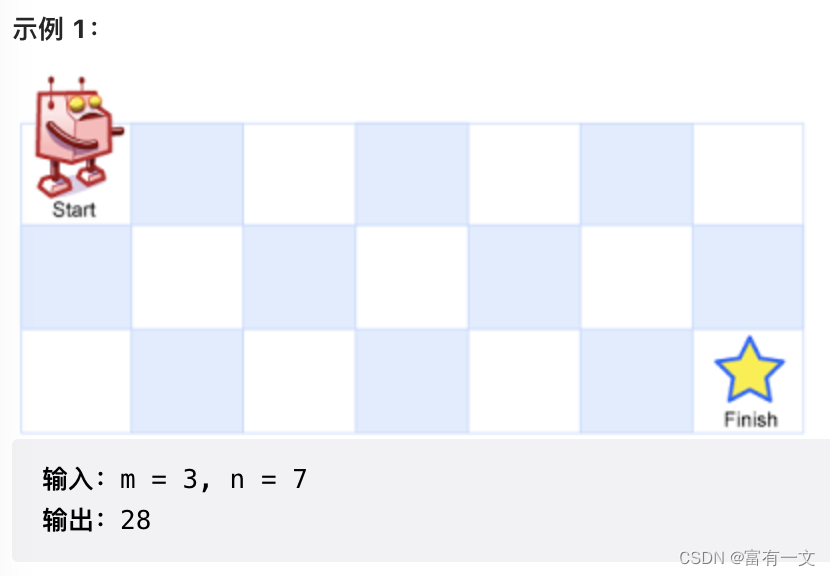
在这里插入图片描述
示例 2：

输入：m = 3, n = 2
输出：3
解释：
从左上角开始，总共有 3 条路径可以到达右下角。
向右 -> 向下 -> 向下
向下 -> 向下 -> 向右
向下 -> 向右 -> 向下

示例 3：
输入：m = 7, n = 3
输出：28

示例 4：
输入：m = 3, n = 3
输出：6

leetcode62

动态规划之带备忘录实现

动态规划五步走解题：动态规划理论基础

1、确定dp数组以及下标的含义
dp[i][j]的定义为：走到第i行j列位置的方法数

2、确定递推公式
机器人只能向下或者向右移动一步，因此对于第i行j列位置的方法数，应该是第i-1行j列的方法数加上第i行j-1列的方法数：
dp[i][j] = dp[i-1][j] + dp[i][j-1]

3、dp数组如何初始化
由题目可知，第0行一直向右移动，只有一种方法，因此dp[0][j] = 1;
第0列一直向下移动，只有一种方法，因此dp[i][0] = 1
即初始化为类似下表：

1	1	1	1
1
1

4、确定遍历顺序
dp[i][j]是依赖 dp[i-1] [j] 和 dp[i][j-1]，那么遍历的顺序一定是从前到后遍历的

5、举例推导dp数组
当m=3，n=7时推导表格如下：
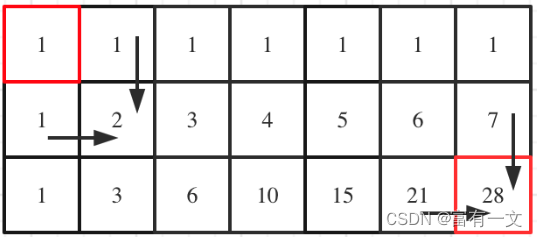
在这里插入图片描述

Java完整代码

class Solution {
    public int uniquePaths(int m, int n) {
        int [][] dp = new int[m][n];

        // 初始化
        // 向右移动
        for (int i = 0; i < n; i++) {
            dp[0][i] = 1;
        }

        // 向下移动
        for (int i = 0; i < m; i++) {
            dp[i][0] = 1;
        }

        for (int i = 1; i < m; i++) {
            for (int j = 1; j < n; j++) {
                dp[i][j] = dp[i-1][j] + dp[i][j-1];
            }
        }

        return dp[m-1][n-1];
    }
}

63. 不同路径 II

题目详情

一个机器人位于一个 m x n 网格的左上角（起始点在下图中标记为 “Start” ）。

机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角（在下图中标记为 “Finish”）。

现在考虑网格中有障碍物。那么从左上角到右下角将会有多少条不同的路径？

网格中的障碍物和空位置分别用 1 和 0 来表示。

leetcode 63

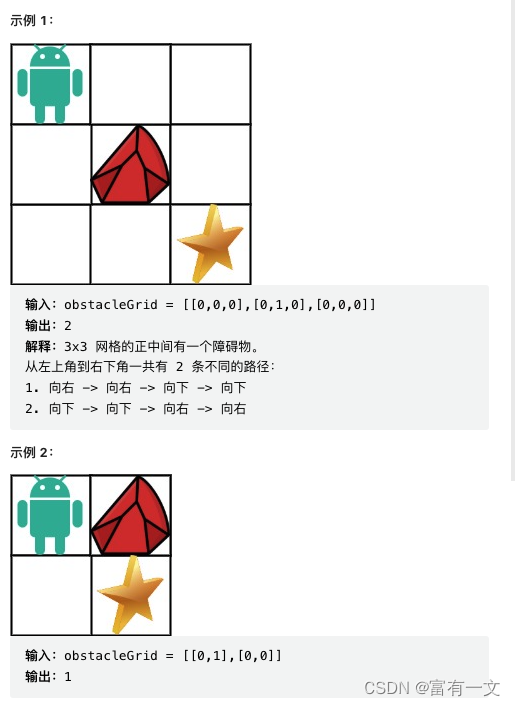
在这里插入图片描述

动态规划之带备忘录实现

本题实现的动态规划想法和上面一道是一模一样的，唯一值得注意的是，应该怎么去解决遇到障碍后的处理。

动态规划五步走解题：动态规划理论基础

1、确定dp数组以及下标的含义

dp[i][j]的定义为：走到第i行j列位置的方法数

2、确定递推公式
机器人只能向下或者向右移动一步，因此对于第i行j列位置的方法数，应该是第i-1行j列的方法数加上第i行j-1列的方法数：
dp[i][j] = dp[i-1][j] + dp[i][j-1]
如果第i行j列是障碍，则dp[i][j]=0

3、dp数组如何初始化
由题目可知，第0行一直向右移动，只有一种方法，因此dp[0][j] = 1;
第0列一直向下移动，只有一种方法，因此dp[i][0] = 1
遇到障碍和障碍之后的点都应该是0
即初始化为类似下表：

1	1	0	0
1
0

4、确定遍历顺序
dp[i][j]是依赖 dp[i-1] [j] 和 dp[i][j-1]，那么遍历的顺序一定是从前到后遍历的

5、举例推导dp数组
如图所示：
在这里插入图片描述
推导过程如下：

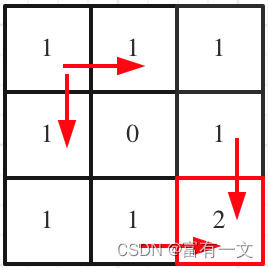
Java完整代码

class Solution {
    public int uniquePathsWithObstacles(int[][] obstacleGrid) {
        int raw = obstacleGrid.length;
        int lie = obstacleGrid[0].length;

        int [][] dp = new int[raw][lie];
        // 初始化

        // 向右移动
        for (int i = 0; i < lie; i++) {
            if (obstacleGrid[0][i] == 1) {
                // 第0行某处有障碍
                break;  // dp数组默认初始化为0
            }
            dp[0][i] = 1;
        }
        // 向下移动
        for (int i = 0; i < raw; i++) {
            if (obstacleGrid[i][0] == 1) {
                // 第0列某处有障碍
                break;  // dp数组默认初始化为0
            }
            dp[i][0] = 1;
        }

        for (int i = 1; i < raw; i++) {
            for (int j = 1; j < lie; j++) {
                if (obstacleGrid[i][j] == 1) {
                    // 该处有障碍
                    dp[i][j] = 0;
                } else {
                    dp[i][j] = dp[i-1][j] + dp[i][j-1];
                }
                
            }
        }
        return dp[raw-1][lie-1];
    }
}