这篇论文主要提出并验证了一种新型的混合智能模型(PSOSVM-CNN-GRU-Attention),用于准确预测滑坡的点位移,并构建可靠的位移预测区间。通过对Baishuihe滑坡和Shuping滑坡的案例分析,展示了该模型的出色性能。
[1] Zai D, Pang R, Xu B, et al. A novel data-driven hybrid intelligent prediction model for reservoir landslide displacement[J]. Bulletin of Engineering Geology and the Environment, 2024, 83(12): 493.
期刊
Bulletin of Engineering Geology and the Environment
《工程地质与环境学报》
日期 : 2024-12
Authors:
Dezhi Zai¹²(Researchgate), Rui Pang¹²³, Bin Xu¹², Jun Liu¹²
Affiliations:
¹ 大连理工大学建设工程学院,中国辽宁省大连市高新园区凌水路2号,116024
² 大连理工大学 海岸和近海工程国家重点实验室,中国辽宁省大连市高新园区凌水路2号,116024
³ 天津大学 水力学与山区河流开发保护国家重点实验室,中国天津市,300072
-
模型提出与验证:提出的混合智能模型结合了粒子群优化支持向量机(PSO-SVM)、卷积神经网络(CNN)、门控循环单元(GRU)和注意力机制,能够提高滑坡点位移预测的准确性,尤其是能够有效捕捉位移变化的关键时刻。
-
性能评估:通过与其他现有方法的比较,本文模型在Baishuihe滑坡和Shuping滑坡上的预测精度显著提高。特别是,模型能够在滑坡发生位移突变时提供较为精准的预测,且具有较小的误差(RMSE、MAE和MAPE值较低)。
-
位移区间预测:除了点位移预测,所提模型还能够构建可靠的位移预测区间,这对于决策者而言,可以帮助采取更为有效的灾害防治措施。
-
理论与实际应用差距:尽管该模型表现优秀,但作者指出,单一监测点的位移不足以全面反映滑坡的整体变形,因此未来的研究应考虑多个监测点的位移序列,并建立空间相关性,从而提高预测的全面性和准确性。
-
结论:本文提出的模型不仅可以预测已知时间序列的滑坡位移,还能对未知时间序列进行预测,并能够在滑坡位移突变的早期阶段提供预警,这对于滑坡灾害的预防和减轻灾害影响具有重要意义。
总的来说,论文展示了一种高效、准确的滑坡位移预测方法,并为未来的滑坡灾害预警和风险评估提供了有力的技术支持。
【论文阅读21】-PSOSVM-CNN-GRU-Attention-滑坡预测
- **摘要**
- **引言**
- 方法
- 滑坡位移分解
- 滑坡位移预测
- 评估指标
- 研究材料
- 白水河滑坡
- **Shuping滑坡**
- **结果**
- **点位移预测**
- **位移区间预测**
- **讨论**
- **结论**
摘要
滑坡监测与预警中,位移预测的准确性和可靠性至关重要。滑坡位移数据属于复杂的非线性时间序列。尽管已有部分研究采用动态模型对滑坡位移进行预测,但大多仅关注点位移的预测,因滑坡预测本身存在的不确定性,难以保障预测结果的可靠性。本文提出了一种新颖的混合智能预测模型,以提高水库滑坡点位移的预测精度,并构建可靠的位移预测区间。具体而言,采用粒子群优化支持向量机(PSO-SVM)预测趋势位移,设计卷积神经网络-门控循环单元-注意力机制(CNN-GRU-Attention)模型预测周期位移。此外,该混合模型能够基于滑坡时间序列直接构建所需的位移预测区间。以白水河和树坪滑坡为案例,验证了所提模型的优越性能。结果表明,该模型在预测精度方面表现更佳,且能够构建可靠的位移预测区间。此外,该模型还可用于未知位移时间序列的预测,并在位移突变的早期阶段提供滑坡预警。本研究有助于提升滑坡风险评估与灾害预警能力,为滑坡灾害防治提供了可靠的科学指导。
关键词
水库滑坡 · 点位移预测 · 位移区间预测 · PSO-SVM · CNN-GRU-Attention
引言
引出话题
滑坡作为一种常见的自然灾害,在全球范围内广泛分布(Bhuyan 等,2024;Casagli 等,2023;Zai 等,2021)。三峡库区(TGRA)由于其特殊的地质条件和外部触发因素,已成为滑坡灾害的集中易发区(Tang 等,2019)。截至目前,三峡库区已识别出超过7,000处地质灾害隐患点,严重威胁着当地居民的生命财产安全。例如,2003年的黔江坪滑坡造成了24人死亡,直接经济损失达700万美元(Wang 等,2004)。准确的位移预测在滑坡风险管理和预警系统中起着关键作用,有助于显著降低滑坡灾害的发生率。
研究现状
当前,滑坡位移预测模型主要分为物理模型和数据驱动模型。物理模型通过模型试验(Wang 和 Lin,2011)或蠕变理论(Saito,1965)来预测滑坡行为,在揭示滑坡机制方面发挥着重要作用(Pang 等,2021;Zai 等,2023)。然而,物理模型存在耗时、成本高以及适用场景有限等问题。相比之下,数据驱动模型因其低成本和高精度而越来越受到学者们的青睐。反向传播神经网络(BPNN)(Bui 等,2018;Du 等,2013)、支持向量机(SVM)(Ma 等,2022b;Miao 等,2018;Zhang 等,2021;Zhou 等,2016)和极限学习机(ELM)(Cao 等,2016;Huang 等,2017;Li 等,2018;Shihabudheen 等,2017)已被广泛应用于水库滑坡位移预测中。然而,上述机器学习方法均为静态模型,对于非线性动态演化的滑坡位移时间序列预测精度较低。
长短期记忆网络(LSTM)和门控循环单元(GRU)作为循环神经网络的扩展形式,不仅具备自适应学习能力,还能捕捉时间序列中的长期依赖关系,因此在滑坡位移预测中表现优异(Liu 等,2020b;Wang 等,2023;Yang 等,2023)。与 LSTM 相比,GRU 结构更简单、参数更少,同时仍能保持良好的预测精度,因而应用广泛。Zhang 等(2022a)采用 GRU 模型对九仙坪滑坡的趋势和周期位移进行建模,并证实其优于静态模型的预测性能。Zhang 等(2022b)采用 GRU 模型预测草家沱滑坡的周期性位移,强调了在水库滑坡预测中捕捉动态特征的重要性。Nava 等(2023)对包括白水河滑坡在内的四个地理位置和地质条件各异的滑坡进行了研究,基于七种模型对比分析,结果显示 GRU 模型具有较强的泛化能力。因此,本文以 GRU 模型为基础,构建了一个稳健的水库滑坡位移混合智能预测模型。
存在问题
目前,大多数滑坡位移预测模型为确定性模型,主要关注点位移预测精度的提升(Wu 等,2022;Yang 等,2024)。然而,滑坡位移预测面临诸多不确定性,如数据采集与处理误差、预测模型本身的不确定性等,这些因素削弱了点预测结果的可信度。位移区间预测被公认为是一种有效的减缓不确定性的方法(Gong 等,2022)。自助法(Bootstrap)和上下界估计法(Lower Upper Bound Estimation)是当前时间序列区间预测中较为常用的方法,并已被成功应用于水库滑坡位移区间预测中(Bai 等,2022;Lian 等,2016;Ma 等,2018;Wang 等,2019)。然而,已有研究大多基于静态机器学习模型构建预测区间,未考虑时间序列数据中的长期依赖特征。
本文方法
为解决上述问题,本文提出了一种可基于滑坡时间序列数据直接构建预测区间的新型模型,具有高可靠性、计算过程简单、易于实现等优势。滑坡位移预测区间的构建对于辅助决策者制定防灾减灾措施具有重要意义。
本文旨在提出一种新型的智能预测模型(PSO-SVM-CNN-GRU-Attention),用于水库滑坡位移的预测。该模型不仅提升了点位移预测的精度,还能构建可靠的位移预测区间,从而降低预测的不确定性。本文结构安排如下:“方法”部分介绍了滑坡位移的分解、预测及评估指标;“数据与材料”部分概述了研究滑坡及其数据分析细节;“结果”部分展示了点位移和区间位移预测的结果;最后为“讨论”和“结论”部分。
方法
本文主要包括四个步骤:位移分解、影响因素分析、位移预测以及模型评估。主要研究框架如图1所示,所涉及的方法将在以下各节中详细介绍。

滑坡位移分解
通常,由于地质条件等内在因素以及库水位、降雨等外在因素的影响,水库滑坡的位移表现出非平稳特性。若直接利用模型对滑坡位移进行预测,可能会导致较大的误差。因此,有必要对位移进行分解,并分别对各组成部分进行预测。
滑坡总位移被分解为两个分量:
1)趋势位移,反映长期变化;
2)周期位移,反映短期波动(Du et al. 2013)。
其计算过程如下:
D ( t ) = T ( t ) + P ( t ) D(t) = T(t) + P(t) D(t)=T(t)+P(t)
其中, T ( t ) T(t) T(t) 表示趋势位移, P ( t ) P(t) P(t) 表示周期位移。
滑坡位移时间序列的分解方法有多种,包括:
- 简单移动平均法(SMA)(Miao et al. 2018;Yang et al. 2019;Zhang et al. 2022a)
- 双指数平滑法(Huang et al. 2017;Xing et al. 2020)
- 经验模态分解法(EMD)(Meng et al. 2023;Xu and Niu 2018)
本研究采用简单移动平均法(SMA) 来计算趋势位移,因其方法简便,且不依赖经验参数。其计算公式如下:
T ( t ) = 1 k ∑ i = t − k + 1 t S i T(t) = \frac{1}{k} \sum_{i=t-k+1}^{t} S_i T(t)=k1i=t−k+1∑tSi
其中, S t S_t St 表示时刻 t t t 观测到的累计位移, k k k 表示移动平均周期数,本文中设为 12 12 12。
滑坡位移预测
支持向量机(SVM)(Cortes 和 Vapnik 1995)是一种非线性回归预测方法,能够通过学习历史数据的趋势来预测未来值。在 SVM 中,时间序列数据被映射到一个高维特征空间中,并通过核函数进行计算。本文中采用径向基核函数进行建模。SVM 即使在样本量较小的情况下也能实现较为准确的预测。然而,SVM 的预测结果对模型参数较为敏感。为提高预测的精度与鲁棒性,引入了粒子群优化算法(PSO)(Kennedy 和 Eberhart 1995)对 SVM 参数进行优化。PSO 是一种群体智能优化算法,模拟鸟群觅食行为,通过不断迭代搜索最优解,能有效避免陷入局部最优。目前,PSO-SVM 常被用作时间序列预测的基准模型。
CNN-GRU-Attention 模型由三个部分组成:一维卷积神经网络(CNN)、门控循环单元(GRU)和注意力机制。
CNN 通过卷积与池化操作能够有效提取时间序列中的局部特征(Pei et al. 2021;Youssef et al. 2022),降低数据维度和复杂度。具体而言,1D CNN 使用大小为 3 的卷积核对时间序列进行卷积运算以提取局部特征,同时通过最大池化操作保留位移序列中显著特征(如图 2a 所示)。

GRU(Chung et al. 2014)采用门控机制,能有效捕捉时间序列中的长期依赖特性。通过更新门 u t u_t ut 和重置门 r t r_t rt 控制信息的流动与遗忘,从而更好地获取时间序列中的动态模式与趋势。更新门决定当前时刻需保留多少新信息,而重置门决定前一时刻的信息对当前时刻的影响程度(如图 2b 所示)。
注意力机制(Vaswani et al. 2017)对时间序列中的不同部分赋予不同权重,从而聚焦于关键时刻以提高预测精度。其计算过程包括三个主要步骤:相似度计算、权重归一化和加权求和,详见图 2c。
GRU 的计算公式如下(图 2b 所示):
- h t h_t ht、 h t − 1 h_{t-1} ht−1 表示当前时刻和前一时刻的隐藏状态;
- x t x_t xt 表示当前输入, h ~ t \tilde{h}_t h~t 为候选隐藏状态;
- σ ( t ) \sigma(t) σ(t) 和 tanh ( t ) \tanh(t) tanh(t) 分别为 Sigmoid 函数和双曲正切函数;
- w i w_i wi 和 b i b_i bi( i = r , u , h i = r, u, h i=r,u,h)分别为对应的权重和偏置;
- ⊙ \odot ⊙ 表示按元素乘法。
滑坡位移区间预测过程如图 3 所示。首先,从原始滑坡时间序列数据中分别生成 5% 和 10% 的宽裕区间数据集,并分别输入至所提模型中。趋势位移由 PSO-SVM 预测获得,周期位移区间则由 CNN-GRU-Attention 预测获得,最终通过叠加趋势位移与周期位移区间来生成最终的宽裕区间。

评估指标
模型性能需通过一系列评估指标进行定量分析。对于滑坡点位移预测,采用以下指标:
- 均方根误差(RMSE)
- 平均绝对误差(MAE)
- 平均绝对百分比误差(MAPE)
- 决定系数( R 2 R^2 R2)(Wang et al. 2022)
其计算表达式如下:
RMSE = 1 n ∑ i = 1 n ( y i − y ^ i ) 2 \text{RMSE} = \sqrt{ \frac{1}{n} \sum_{i=1}^{n} (y_i - \hat{y}_i)^2 } RMSE=n1i=1∑n(yi−y^i)2
MAE = 1 n ∑ i = 1 n ∣ y i − y ^ i ∣ \text{MAE} = \frac{1}{n} \sum_{i=1}^{n} |y_i - \hat{y}_i| MAE=n1i=1∑n∣yi−y^i∣
MAPE = 100 % n ∑ i = 1 n ∣ y i − y ^ i y i ∣ \text{MAPE} = \frac{100\%}{n} \sum_{i=1}^{n} \left| \frac{y_i - \hat{y}_i}{y_i} \right| MAPE=n100%i=1∑n yiyi−y^i
R 2 = 1 − ∑ i = 1 n ( y i − y ^ i ) 2 ∑ i = 1 n ( y i − y ˉ ) 2 R^2 = 1 - \frac{ \sum_{i=1}^{n} (y_i - \hat{y}_i)^2 }{ \sum_{i=1}^{n} (y_i - \bar{y})^2 } R2=1−∑i=1n(yi−yˉ)2∑i=1n(yi−y^i)2
其中, n n n 为测试集长度, y i y_i yi 表示实际位移值, y ^ i \hat{y}_i y^i 为预测值, y ˉ \bar{y} yˉ 为实际值的平均值。
RMSE、MAE 和 MAPE 从不同误差角度评估模型的预测能力,值越小代表性能越优。 R 2 R^2 R2 越接近于 1,说明模型的预测效果越好。
对于滑坡位移区间预测,采用预测区间覆盖率(PICP)(Shrestha and Solomatine 2006)和预测区间归一化宽度(PINRW)(Quan et al. 2014)作为评估指标:
PICP = 1 n ∑ i = 1 n s i \text{PICP} = \frac{1}{n} \sum_{i=1}^{n} s_i PICP=n1i=1∑nsi
其中, L ( x i ) L(x_i) L(xi) 和 U ( x i ) U(x_i) U(xi) 分别为第 i i i 个样本的预测区间下界和上界, s i = 1 s_i = 1 si=1 表示真实值落在预测区间内, s i = 0 s_i = 0 si=0 表示未落入区间。
PICP 的取值范围为 [ 0 , 1 ] [0, 1] [0,1],数值越大表示模型越可靠。但过宽的预测区间虽然可能提升覆盖率,却也增加了不确定性。因此还需通过 PINRW 评估模型的不确定性,其值越小,表示不确定性越低。
研究材料
由于特殊的地质环境及外部诱发因素,三峡库区(TGRA)被认为是全球最活跃的滑坡多发区之一。白水河滑坡和树坪滑坡是具有代表性的库岸滑坡,受到学者们的广泛关注(Liu et al. 2020a;Long et al. 2022;Moeineddin et al. 2023;Seguí et al. 2020;Seguí and Veveakis 2022)。这两处滑坡的分布情况和地理位置如图 4 所示。

白水河滑坡
白水河滑坡位于湖北省秭归县沙镇溪镇,距三峡大坝约 56 公里。滑坡的卫星图像(来源:Google Earth)及地形图如图 5 所示。滑坡后缘高程约为 400 m,前缘位于长江水位以下。滑坡整体坡度约为
3
0
∘
30^\circ
30∘,南北向长约 600 m,东西向宽约 700 m,平均厚度约 30 m,总体积约为
1.26
×
1
0
7
m
3
1.26 \times 10^7~\text{m}^3
1.26×107 m3。地层岩性主要由砂岩和泥岩构成。

根据滑坡变形差异,研究区域被划分为预警区(Zone A)和稳定区(Zone B)。在预警区布设了 6 个监测点,其中 ZG118(见图 5b)位于滑坡中心,具有较长且保存完好的位移时间序列。因此,本文选用该监测点的数据进行白水河滑坡的研究。
滑坡位移、降雨量及库水位变化情况如图 6 所示,时间序列范围为 2006 年 1 月至 2018 年 9 月。从图中可以明显观察到滑坡位移呈现阶梯状特征:每年 5 月至 9 月为显著增长期,而 10 月至次年 4 月则为相对稳定期。这一现象的形成原因主要有两个方面:

- 水位下降引起的渗流力向滑坡体外部作用,削弱了边坡稳定性;
- 强降雨削弱土体强度,进一步加剧滑坡变形。
本文采用简单移动平均法(SMA)对累积位移进行分解,分解结果如图 7 所示。可以看出,趋势位移随时间单调增加,而滑坡曲线的阶梯状特征主要由周期性位移造成。

数据集被划分为训练集和测试集,训练集包含 121 期数据(2006.12–2016.12),测试集包含 21 期数据(2017.01–2018.09)。为提高模型的泛化能力并降低过拟合风险,引入了正则化与 dropout 技术。
- 对于趋势位移的预测,采用 PSO-SVM 模型,粒子群算法迭代次数设为 200,种群规模为 20。
- 周期位移预测采用 CNN-GRU-Attention 模型,模型参数通过网格搜索算法确定:
- CNN 输出通道数为 30;
- GRU 层数为 2,每层单元数为 600;
- 训练轮次(epoch)为 1000。
为减小模型不确定性对预测精度的影响,每个模型重复训练 20 次,并取平均作为最终结果。
周期位移与库水位变化及季节性降雨密切相关(Du et al. 2013;Luo et al. 2023;Miao et al. 2022;Zhang et al. 2021),因此在周期位移预测中考虑这些因素至关重要。此外,滑坡体自身条件也是影响其变形的重要因素,本文一并考虑。
为分析各影响因素与周期位移的相关性,采用灰色关联分析法(Kuo et al. 2008)。分析结果列于表 1,所有关联度均大于 0.7,表明所选因素在周期位移预测中的合理性。
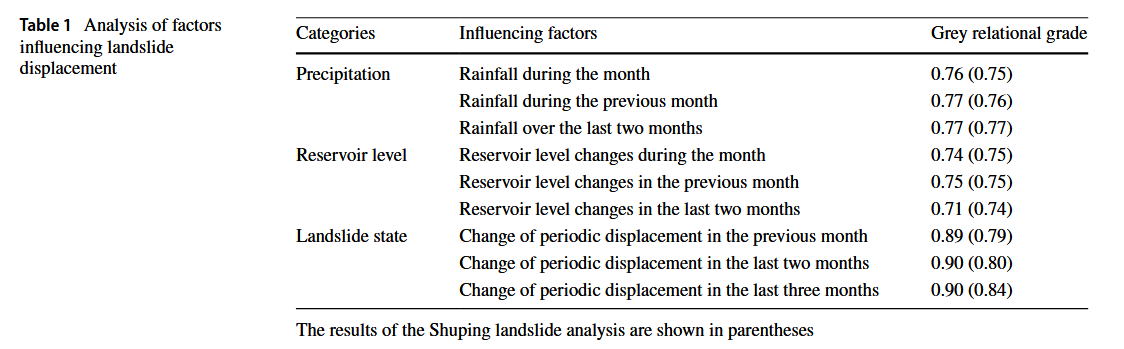
由于不同特征的取值范围存在差异,本文在预测与相关性分析中采用了 Min–Max 归一化方法,将所有数据线性映射至区间 [ 0 , 1 ] [0, 1] [0,1],以增强模型训练效果并提升预测精度。
Shuping滑坡
Shuping滑坡位于湖北省秭归县,距离三峡大坝约47公里。图8展示了来自无人机的正射影像和Shuping滑坡的地形图。该滑坡的整体形态类似于椅子形状,后缘的海拔为400米,前缘则被长江的水位淹没。滑坡在南北方向长800米,东西方向宽700米,覆盖面积约为5.5 × 10^5平方米。其平均厚度约为50米,总体积约为2.75 × 10^7立方米。

根据多年来的变形特征,Shuping滑坡被划分为两个不同的区域:主要滑动区(区域A)和影响区(区域B)。选择了位于主要滑动区的监测点ZG85(见图8b)的位移时间序列作为代表,来分析Shuping滑坡。
图9展示了Shuping滑坡的位移、降水量和水库水位数据。趋势位移和周期位移如图10所示。在2014年之前,滑坡位移曲线呈现明显的阶梯型特征。周期位移较小,而趋势位移在2014年后接近总位移。Shuping滑坡的训练集与Baishuihe滑坡相同(2006.12–2016.12),但测试集略有不同(2017.01–2018.12)。位移预测方法与Baishuihe滑坡使用的方法一致,只有少数参数有所不同。GRU层数设为2,每层200个单元。此外,周期位移的影响因素和相关系数如表1所示。


结果
点位移预测
Baishuihe滑坡的趋势和周期位移的预测结果如图11所示。对于趋势位移,PSO-SVM模型与监测值表现出极好的吻合,最大绝对误差仅为3.42毫米。在周期位移方面,CNN-GRU-Attention模型与实测值的结果一致,主要误差出现在位移突变阶段。值得注意的是,模型的预测结果落后于实测值,这是大多数时间序列预测模型常遇到的挑战。

为了突出所提模型的优异表现,进行了与几种不同混合模型的比较。这些模型的位移预测结果如图12和表2所示。所有模型均能恰当地描述测试集中的位移趋势。与PSO-SVM相比,以GRU为基础框架的模型取得了更好的预测结果,尤其是结合了1-D CNN和注意力机制的模型。PSO-SVM-GRU模型的RMSE、MAE和MAPE分别是PSO-SVM模型预测值的67.39%、63.61%和64.13%。此外,R²提高了5.72%。所提模型的RMSE、MAE和MAPE分别是PSO-SVM-GRU模型预测值的74.40%、69.76%和70.08%。


此外,R²提高了0.95%。总之,所提模型在Baishuihe滑坡的案例研究中表现出色。Baishuihe滑坡的监测点ZG118在2018年10月施工过程中受损,导致后续位移数据无法获得。根据已知的降水量和水库水位,训练后的模型被用于直接预测未来三个月的滑坡位移,结果如图13所示。通过比较数据集中同月位移变化,表明2018.10–2018.12期间的位移预测结果是可信的。值得注意的是,该模型能够捕捉到Baishuihe滑坡位移突变的早期阶段。这表明,所提模型有潜力作为滑坡的预警系统,对滑坡灾害的预防和减灾具有重要意义。

为了验证该模型的强大泛化能力,考虑了Shuping滑坡的时间序列数据,并呈现了趋势和周期位移的预测结果,如图14所示。关于趋势位移,PSO-SVM模型的预测结果与监测值几乎吻合,最大绝对误差仅为1.32毫米。在周期位移方面,CNN-GRU-Attention模型的预测结果与实测值大体一致,误差主要出现在2017.05–2017.07期间。与Baishuihe滑坡的情况类似,预测结果也呈现一定的滞后。Shuping滑坡不同模型的位移预测结果如图15和表3所示。如同Baishuihe滑坡一样,所有模型成功捕捉到了Shuping滑坡位移的总体趋势。特别是,以GRU为核心框架的模型在预测结果上超越了PSO-SVM模型。所提模型在测试集上取得了最佳表现,RMSE、MAE、MAPE和R²分别为11.61毫米、8.49毫米、0.21%和0.9359。与PSO-SVM模型相比,所提模型在RMSE、MAE和MAPE上分别减少了34.21%、42.83%和42.76%,R²提高了7.38%。因此,本文所提模型在滑坡点位移预测中具有优越的性能。



位移区间预测
由于存在多种不确定性,模型预测值与实际值之间总会存在差异。仅依靠点预测可能不足以说服决策者。因此,为滑坡位移创建预测区间是一个更优的解决方案。Baishuihe滑坡测试集的预测位移区间如图16所示。除了2017年7月的变形值外,所有其他值均落在5%富裕区间内,而所有测试集中的观测值都包含在10%富裕区间内。对于5%富裕区间,位移区间的最大宽度为2017年8月的117毫米,最小宽度为2018年2月的28毫米。对于10%富裕区间,位移区间的最大宽度为2018年10月的187毫米,最小宽度为2017年4月的37毫米。预测区间的宽度在滑坡位移快速增加的时期要大于在位移缓慢增加的时期。此外,所提方法为滑坡位移的未知时间序列(2018.10–2018.12)提供了可靠的预测区间。

Shuping滑坡的预测位移区间如图17所示。与Baishuihe滑坡的预测位移区间类似,5%富裕区间涵盖了大多数变形值,而10%富裕区间则包含了所有观测值。这表明,本文所提出的位移区间预测方法是非常可信的。5%富裕区间的位移区间宽度在10毫米至42毫米之间,10%富裕区间的宽度则在21毫米至70毫米之间。

类似地,位移快速增加的时期的预测区间宽度要大于位移缓慢增加的时期。PICP和PINRW是用于评估预测区间的指标,其计算结果列在表4中。对于Baishuihe和Shuping滑坡,采用5%富裕区间并且PINRW较低时,产生了相对满意的PICP。尽管10%富裕区间实现了最佳的PICP,但其PINRW相对较差。因此,在考虑预测区间时,需要在PICP和PINRW之间取得平衡,并根据具体情况确定富裕区间的范围。

讨论
为了验证所提模型的出色表现,本文分析了Baishuihe滑坡和Shuping滑坡。根据评估指标,本研究的预测结果优于某些先前的研究(Nava等,2023年;Wang等,2022年;Yang等,2023年)。其原因可以归结为两个方面:1) 所提模型结合了CNN和注意力机制,能够有效捕捉时间序列中的局部特征,聚焦于位移突变的关键时刻,从而增强了模型的特征提取能力。2) 与以往研究相比,本文使用的数据集具有更长的时间序列,使得模型能够充分挖掘数据之间的内在关系。特别是对于深度学习算法,数据集的大小对预测结果有着巨大的影响。因此,未来的研究应强调这一点。
尽管所提模型在Baishuihe和Shuping滑坡中展示了许多相似之处,但也存在一些区别。Baishuihe滑坡的RMSE、MAE和MAPE分别为18.25毫米、12.30毫米和0.4%,而Shuping滑坡的分别为11.61毫米、8.49毫米和0.21%。该模型在Shuping滑坡的预测表现优于Baishuihe滑坡的预测结果,这与其他研究的结果一致(Ma等,2022年;Yang等,2023年)。此外,Baishuihe滑坡的位移区间宽度较大(105毫米与45毫米,或59毫米与23毫米),推测是由于Baishuihe滑坡在测试集中的位移变化较为剧烈。本研究集中于单点滑坡位移的预测,但理论预测与实际应用之间仍存在较大差距。单一监测点的位移不足以反映滑坡的整体状况。因此,未来的研究应考虑多个监测点的位移序列,建立空间相关性,并实现对滑坡任何点的变形预测。这将有助于弥合理论预测与实际应用之间的差距。
结论
本文提出了一种新型的混合智能模型(PSOSVM-CNN-GRU-Attention),用于准确预测滑坡点位移并构建可靠的位移预测区间。通过对Baishuihe和Shuping滑坡的案例分析,验证了该模型的优异性能。本文的主要结论如下:
- 所提模型相较于本文中的比较模型具有更高的预测精度,突出了1-D CNN和注意力机制的重要性。
- 基于时间序列,所提模型能够直接构建可靠的位移预测区间,有助于促使决策者采取更为科学的措施。
- 所提模型可以根据已知的时间序列预测未知的位移时间序列,对于了解未来滑坡变形趋势具有重要意义。此外,该模型能够在位移突变的初期阶段对滑坡进行预警,这对滑坡灾害的预防和减灾具有重要意义。
本研究为滑坡预测的进展、滑坡风险评估的改进和灾害预警能力的提升做出了贡献。这些研究成果为有效的灾害防治提供了更可靠的科学依据。未来,将通过整合遥感数据和内部监测数据等多源数据,进一步增强模型的输入特征,以提高预测的准确性和可靠性。
致谢
感谢国家冰冻圈与沙漠数据中心提供滑坡时间序列数据(http://www.ncdc.ac.cn)。本研究得到了中国国家重点研发计划(2023YFC3011400)、国家自然科学基金(项目编号52279125、52279096、52379117)、水利工程仿真与安全国家重点实验室开放基金(HESS2302)和海岸与近海工程国家重点实验室青年学者创新基金(LY2301)的资助,对这些财务支持表示衷心感谢。
作者贡献
Dezhi Zai: 方法学、软件、正式分析、原创草稿编写、审稿与编辑。Rui Pang: 概念化、资源、监督、资金获取、项目管理。Bin Xu: 概念化、监督、资金获取。Jun Liu: 资源、监督、资金获取。
数据可用性
数据可根据请求向作者提供。
声明
竞争利益 本文作者声明没有竞争利益。


















