欢迎观看我的博客，如有问题交流，欢迎评论区留言，一定尽快回复！（大家可以去看我的专栏，是所有文章的目录）
　
文章字体风格：
红色文字表示：重难点★✔
蓝色文字表示：思路以及想法★✔
　
如果大家觉得有帮助的话，感谢大家帮忙
点赞！收藏！转发！

A*算法是什么

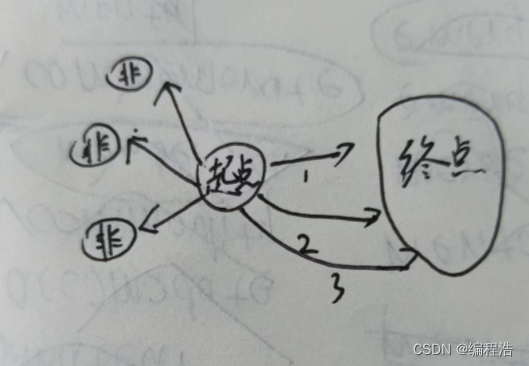
比如如图，我们要搜索从起点到终点的最小距离

起点 一共连接6条边，

我们如果通过 起点的6条边 bfs 搜索 终点

万一搜索的第一挑边是 左上角那条，那么接下来的bfs会优先走这一条，但是这一条如果连接了 特比多边，就会导致，我们的算法时间复杂度非常大

那么我们优化办法就来了，就是

优先走 起点6条边中的 距离终点较 短的 路

怎么实现呢？

我们先从终点往外遍历，记录所有边到终点的距离，那么我们就会知道
起点的6条边中，哪一条边 距离终点较近

优先遍历这条就是了

以上就是A*算法的逻辑
也就是需要 预先处理一下 所有边到终点的最短距离（直接从终点开始遍历）

例题1. 第K短路

原题链接

题意解析

本题求A点到B点
路径长度排名第K 的 路径长度大小 是多少

我们画图自己简单分析一下，可以得出
A点到B点 会有非常非常多的路径走法

那么具体走哪些部分呢？

那就是 先走 距离B较小的路径部分
那么就用到了A*算法思想

我们先预处理一下，B点到所有点的最短距离

然后从A开始走，A点会连接很多点，但是先走 距离A点+距离B点 总和较小的点

如果走到了B那么就不再继续走

但是别的路径还是继续走

直到走到B为K次，那么

此时的路径就是 第K长度

#include <cstring>
#include <iostream>
#include <algorithm>
#include <queue>

#define x first
#define y second

using namespace std;

typedef pair<int, int> PII;
typedef pair<int, PII> PIII;
const int N = 1010, M = 200010;

int n, m, S, T, K;
int h[N], rh[N], e[M], w[M], ne[M], idx;
int dist[N], cnt[N];
bool st[N];

void add(int h[],int a,int b,int c)
{
    e[idx] = b;
    w[idx] = c;
    ne[idx] = h[a];
    h[a] = idx++;
}

void dijkstra()
{
    priority_queue<PII,vector<PII>,greater<PII>> heap;
    heap.push({0,T});//终点
    memset(dist, 0x3f, sizeof dist);
    dist[T] = 0;

    while(heap.size())
    {
        auto t = heap.top();
        heap.pop();

        int ver = t.y;
        if(st[ver]) continue;
        st[ver] = true;

        for(int i=rh[ver];i!=-1;i=ne[i])
        {
            int j = e[i];
            if(dist[j]>dist[ver]+w[i])
            {
                dist[j] = dist[ver] + w[i];
                heap.push({dist[j],j});
            }
        }
    }
}

int astar()
{
    priority_queue<PIII, vector<PIII>, greater<PIII>> heap;
    // 谁的d[u]+f[u]更小 谁先出队列
    heap.push({dist[S], {0, S}});
    while(heap.size())
    {
        auto t = heap.top();
        heap.pop();
        int ver = t.y.y,distance = t.y.x;
        cnt[ver]++;
        //如果终点已经被访问过k次了 则此时的ver就是终点T 返回答案

        if(cnt[T]==K) return distance;

        for(int i=h[ver];i!=-1;i=ne[i])
        {
            int j = e[i];
            /* 
            如果走到一个中间点都cnt[j]>=K，则说明j已经出队k次了，且astar()并没有return distance,
            说明从j出发找不到第k短路(让终点出队k次)，
            即继续让j入队的话依然无解，
            那么就没必要让j继续入队了
            */
            if(cnt[j] < K)
            {
                // 按 真实值+估计值 = d[j]+f[j] = dist[S->t] + w[t->j] + dist[j->T] 堆排
                // 真实值 dist[S->t] = distance+w[i]
                heap.push({distance+w[i]+dist[j],{distance+w[i],j}});
            }
        }
    }
    // 终点没有被访问k次
    return -1;
}

int main()
{
    cin >> m >> n;
    memset(h,-1,sizeof h);
    memset(rh,-1,sizeof rh);
    for(int i=0;i<n;i++)
    {
        int a,b,c;
        cin >> a >> b >> c;
        add(h,a,b,c);
        add(rh,b,a,c);
    }
    cin >> S >> T >> K;
    // 起点==终点时 则d[S→S] = 0 这种情况就要舍去 ,总共第K大变为总共第K+1大 
    if (S == T) K ++ ;
    // 从各点到终点的最短路距离 作为估计函数f[u]
    dijkstra();
    cout << astar();
    return 0;
}

例题2. 八数码

原题链接

这道题，我们可以用 bfs 直接搜索出来 路径

也可以使用 A* 算法优化

也就是 当状态A 会引出n条路径

到底走哪条路径更好呢？

我们可以通过
走到当前路径的步数 + 当前路径到最终状态的最小步数
进而进行A*思想的 优先走法

#include<iostream>
#include<algorithm>
#include<cstring>
#include<unordered_map>
#include<queue>

#define x first
#define y second

using namespace std;

typedef pair<int,string> PIS;

int f(string m)//估计函数
{
    int dt=0;
    for(int i=0;i<9;i++)//这里1~8对应的下标为0~7
    if(m[i]!='x')
    {
        int t=m[i]-'1';//对应下标
        dt=dt+abs(i/3-t/3)+abs(i%3-t%3);//曼哈顿距离
    }
    return dt;//返回总曼哈顿距离
}

string bfs(string start)
{
    string end="12345678x";//终点

    unordered_map<string,int> d;//存储距离
    priority_queue<PIS, vector<PIS>, greater<PIS>> heap;//小根堆,将元素的估计终点距离从小到大排序
    unordered_map<string,pair<string,char>> last;//存储一个元素由哪种状态,经过哪种操作得来,跟前面几题一样

    heap.push({f(start),start});//加入起点
    d[start]=0;//起点到起点的距离为0
    //要将操作数组与坐标变化数组一一对应
    char oper[]="udlr";
    int dx[4]={-1,1,0,0},dy[4]={0,0,-1,1};

    while(heap.size())
    {
        auto t=heap.top();//队头
        heap.pop();//弹出
        string state=t.y;//记录

        if(t.y==end) break;//终点出列的话就退出

        int x,y;//查找x的横纵坐标
        for(int i=0;i<9;i++)
        if(state[i]=='x')
        {
            x=i/3,y=i%3;
            break;
        }

        string init=state;
        for(int i=0;i<4;i++)
        {
            int a=x+dx[i],b=y+dy[i];
            if(a<0||a>=3||b<0||b>=3) continue;//越界就跳过
            swap(state[a*3+b],state[x*3+y]);//交换下标位置
            if(!d.count(state)||d[state]>d[init]+1)//如果没有被记录或者小于记录值
            {
                d[state]=d[init]+1;//更新距离
                heap.push({f(state)+d[state],state});//加入堆中
                last[state]={init,oper[i]};//标记由哪种状态转移而来,并且记录执行的操作
            }
            state=init;//因为要扩展到四个方向,所以要还原
        }
    }

    string ans;
    //跟前面几题原来相同
    while(end!=start)
    {
        ans+=last[end].y;
        end=last[end].x;
    }
    reverse(ans.begin(),ans.end());//将其反转
    return ans;
}

int main()
{
    string start,x,c;
    while(cin>>c)//这样输入可以忽视空格
    {
        start+=c;
        if(c!="x") x+=c;
    }

    int res=0;//统计逆序对的数量
    for(int i=0;i<8;i++)
     for(int j=i+1;j<8;j++)
      if(x[i]>x[j]) 
       res++;

    if(res%2) printf("unsolvable\n");//如果逆序对为奇数,就不可能抵达终点
    else cout<<bfs(start)<<endl;//输出答案

    return 0;
}