数据增强
数据太少可能会过拟合。

# data_transforms中指定了所有图像预处理(变换)操作(图像数据增强)
data_transforms = {
'train': transforms.Compose([transforms.RandomRotation(45), # 随机旋转,-45到45度之间随机选
transforms.CenterCrop(224), # 从中心开始裁剪,裁剪成224*224大小的(因为VGG、Resnet这些经典网络都是用此大小)
transforms.RandomHorizontalFlip(p=0.5), # 随机水平翻转,即有50%的概率翻转
transforms.RandomVerticalFlip(p=0.5), # 随机垂直翻转
transforms.ColorJitter(brightness=0.2, contrast=0.1, saturation=0.1, hue=0.1),
# 参数1为亮度,参数2为对比度,参数3为饱和度,参数4为色相
transforms.RandomGrayscale(p=0.025), # 概率转换成灰度率,如果原来是彩色图,转换后依旧是3通道只是R=G=B
# 转成Tensor格式
transforms.ToTensor(),
# 因为别人的模型标准化了,所以我们拿他的均值,标准差来标准化
transforms.Normalize([0.485, 0.456, 0.406], [0.229, 0.224, 0.225])
]),
'valid': transforms.Compose([transforms.Resize(256),
transforms.CenterCrop(224),
transforms.ToTensor(),
# 验证集的均值和标准差要和测试集一致
transforms.Normalize([0.485, 0.456, 0.406], [0.229, 0.224, 0.225])
]),
}
常用网络模型
VGG-16
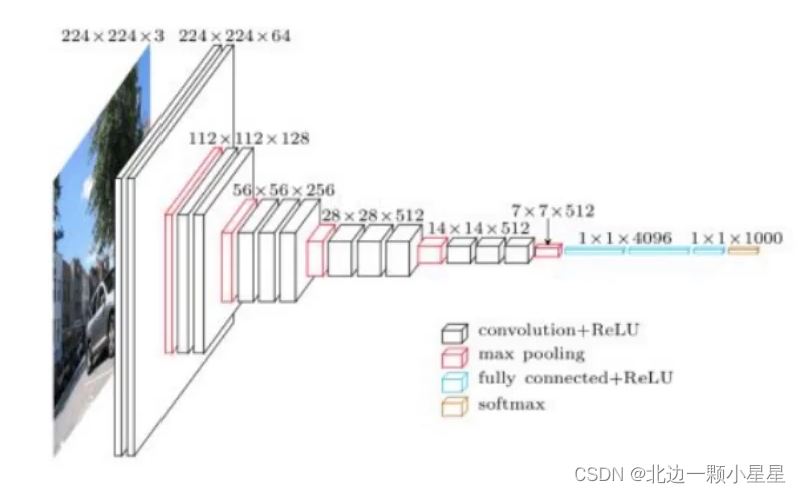
首先是VGG
,也叫作
VGG-16
网络。它
没有那么多超参数,是一种只需要专注于构建卷积层的简单网络。
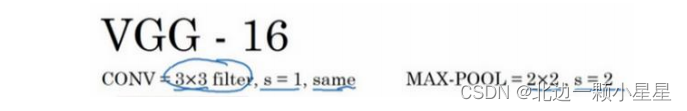
首先用
3×3
,步幅为
1
的过滤器构建卷积层,
padding
参数为
same 卷积(意为卷积之后输出的feature map尺寸保持不变(相对于输入图片)
)中的参数。然后用 一个 2×2
,步幅为
2
的过滤器构建最大池化层。因此
VGG
网络的一大优点是它确实简化了神经网络结构,下面我们具体讲讲这种网络结构。
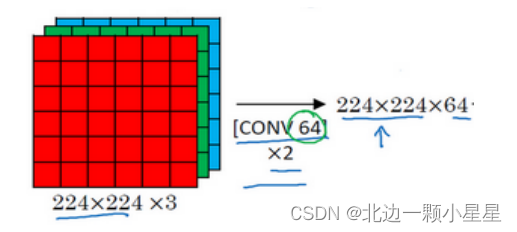
假设要识别这个图像,在最开始的两层用
64
个
3×3
的过滤器对输入图像进行卷积,输出结果是 224×224×64
,因为使用了
same
卷积,通道数量也一样。
VGG-16
其实是一个很深的网络,这里并没有把所有卷积层都画出来。
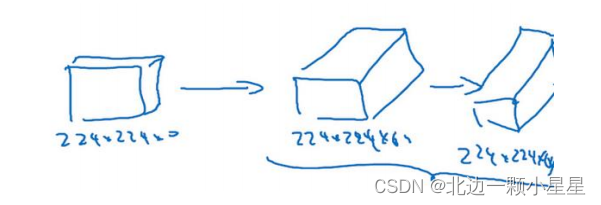
假设这个小图是我们的输入图像,尺寸是
224×224×3
,进行第一个卷积之后得到224×224×64 的特征图,接着还有一层
224×224×64
,得到这样
2
个厚度为
64
的卷积层,意味着我们用 64
个过滤器进行了两次卷积。正如我在前面提到的,这里采用的都是大小为3×3,步幅为
1
的过滤器,并且都是采用
same
卷积,所以我就不再把所有的层都画出来了,
只用一串数字代表这些网络。接下来创建一个池化层,池化层将输入图像进行压缩,从 224×224×64 缩小到多少呢?
没错,减少到
112×112×64
。然后又是若干个卷积层,使用
129 个过滤器,以及一些 same卷积,我们看看输出什么结果,112×112×128.然后进行池化,可以推导出池化后的结果是这样(56×56×128
)。接着再用 256 个相同的过滤器进行三次卷积操作,然后再池化,然后再卷积三次,再池化。如此进行几轮操作后,将最后得到的 7×7×512
的特征图进行全连接操作,得到 4096
个单元,然后进行
softmax
激活,输出从
1000
个对象中识别的结果。
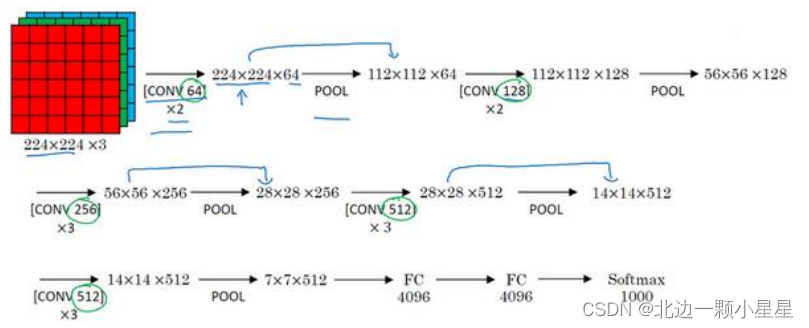
VGG-16
的这个数字
16
,就是指在这个网络中包含
16
个卷积层和全连接层。确实是个很大的网络,总共包含约 1.38
亿个参数,即便以现在的标准来看都算是非常大的网络。但 VGG-16
的结构并不复杂,这点非常吸引人,而且这种网络结构很规整,都是几个卷积层后面跟着可以压缩图像大小的池化层,池化层缩小图像的高度和宽度。同时,卷积层的过滤器数量变化存在一定的规律,由 64
翻倍变成
128
,再到
256
和
512
。作者可能认为 512
已经足够大了,所以后面的层就不再翻倍了。无论如何,每一步都进行翻倍,或者说在每一组卷积层进行过滤器翻倍操作,正是设计此种网络结构的另一个简单原则。
这种相对一致的网络结构对研究者很有吸引力,而它的主要缺点是需要训练的特征数量非常巨大。
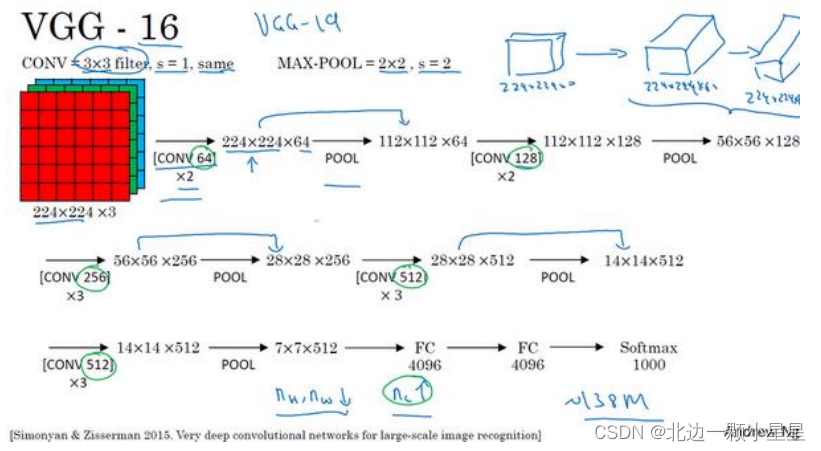
VGG-19
网络,它甚至比
VGG-16 还要大,但由于
VGG-16
的表现几乎和
VGG-19
不分高下,所以很多人还是会使用 VGG-16。VGG-16随着网络的加深,图像的高度和宽度都在以一定的规律不断缩小,每次池化后刚好缩小一半,而通道数量在不断增加,而且刚好也是在每组卷积操作后增加一倍。也就是说,图像缩小的比例和通道数增加的比例是有规律的。
残差网络(ResNets)
因为层数越多可能会反而出现效果更差的效果,为了降低其中不好的层的影响(即相当于权重置0去掉),可以“跳跃连接”跳过这层直接连到下一层,这样深度越深总会达到更好的效果。
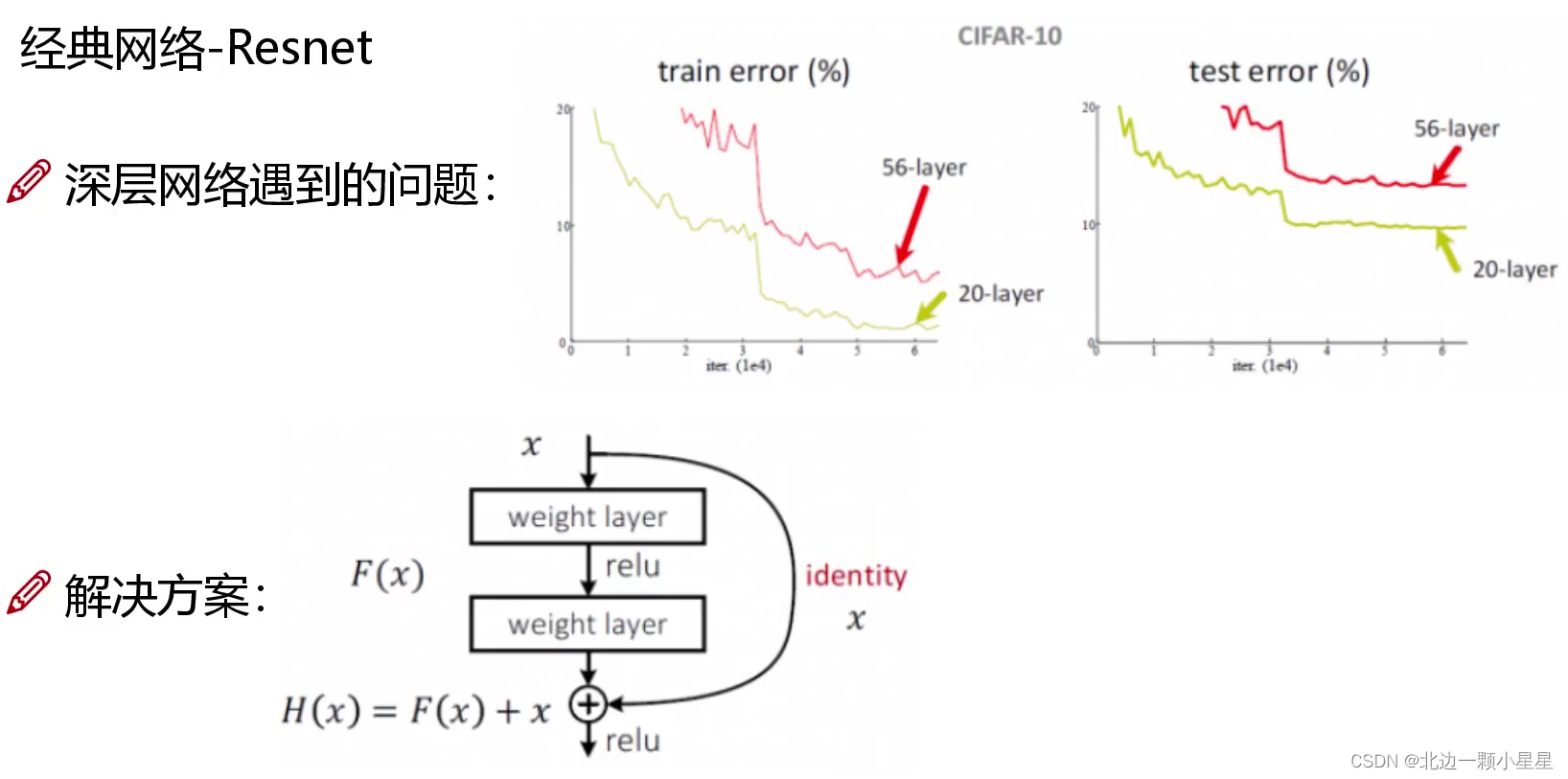
非常非常深的神经网络是很难训练的,因为存在梯度消失和梯度爆炸问题。跳跃连接(
Skip connection
),它可以从某一层网络层获取激活,然后迅速反馈给另外一层,甚至是神经网络的更深层。我们可以利用跳跃连接构建能够训练深度网络的
ResNets
,有时深度能够超过
100
层。
ResNets
是由残差块(
Residual block
)构建的,首先解释一下什么是残差块。
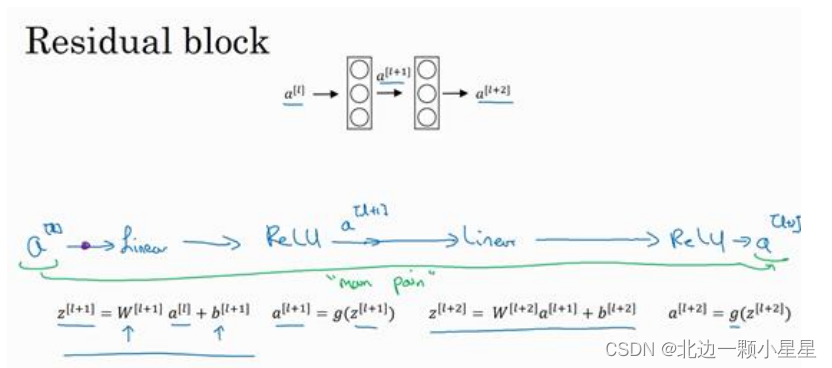

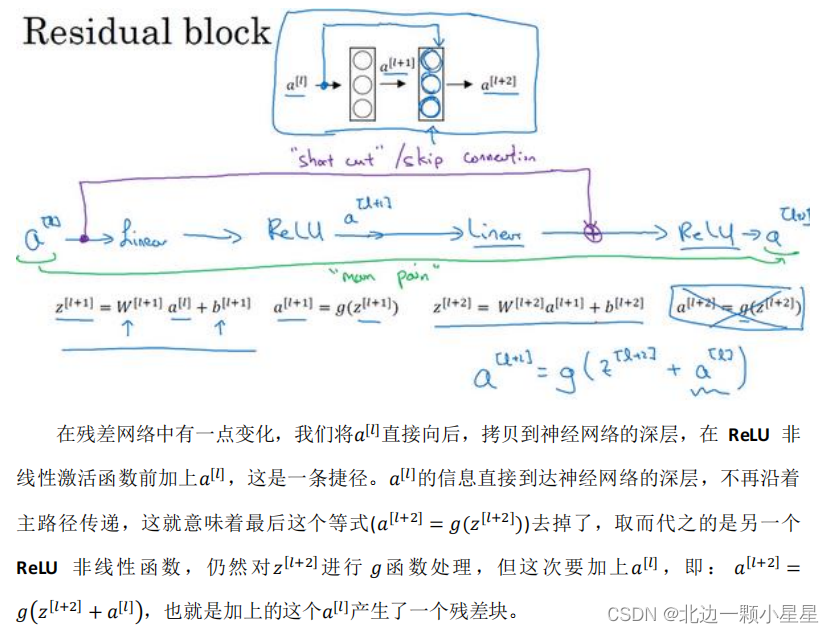
在上面这个图中,我们也可以画一条捷径,直达第二层。实际上这条捷径是在进行
ReLU
非线性激活函数之前加上的,而这里的每一个节点都执行了线性函数和
ReLU 激活函数。所以𝑎 [𝑙]
插入的时机是在线性激活之后,
ReLU激活之前。除了捷径,另一个术语“
跳跃连接”,就是指
𝑎
[𝑙]
跳过一层或者好几层,从而将信息传递到神经网络的更深层。
使用残差块能够训练更深的神经网络。
所以构建一个 ResNet
网络就是通过将很多这样的残差块堆积在一起,形成一个很深神经网络,我们来看看这个网络。

这并不是一个残差网络,而是一个普通网络(Plain network)。
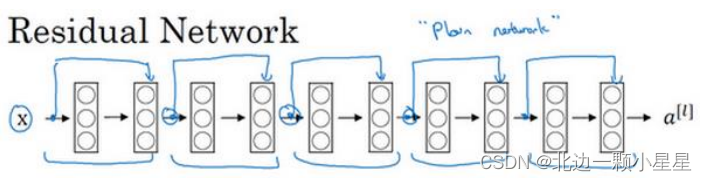
把它变成
ResNet
的方法是加上所有跳跃连接,正如前一张幻灯片中看到的,每两层增加一个捷径,构成一个残差块。如图所示,5
个残差块连接在一起构成一个残差网络。
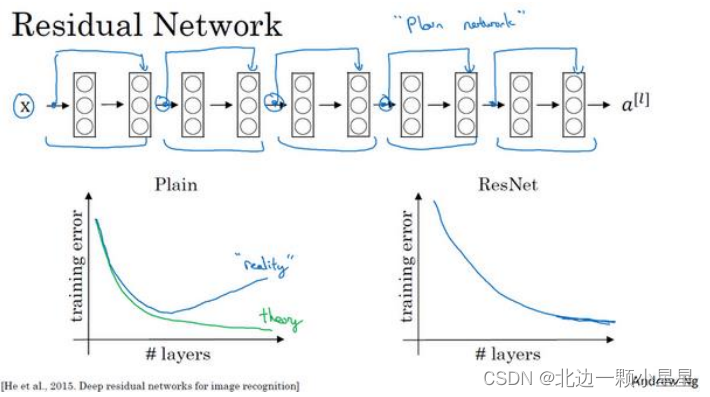
如果我们使用标准优化算法训练一个普通网络,比如说梯度下降法,或者其它热门的优化算法。如果没有残差,没有这些捷径或者跳跃连接,凭经验你会发现随着网络深度的加深,训练错误会先减少,然后增多。而理论上,随着网络深度的加深,应该训练得越来越好才对。也就是说,理论上网络深度越深越好。但实际上,如果没有残差网络,对于一个普通网络来说,深度越深意味着用优化算法越难训练。实际上,随着网络深度的加深,训练错误会越来越多。
但有了
ResNets
就不一样了,即使网络再深,训练的表现却不错,比如说训练误差减少,就算是训练深达 100
层的网络也不例外。有人甚至在1000 多层的神经网络中做过实验,尽管目前我还没有看到太多实际应用。但是对𝑥
的激活,或者这些中间的激活能够到达网络的更深层。这种方式确实有助于解决梯度消失和梯度爆炸问题,让我们在训练更深网络的同时,又能保证良好的性能。也许从另外一个角度来看,随着网络越来深,网络连接会变得臃肿,但是 ResNet
确实在训练深度网络方面非常有效。
迁移学习
为什么要迁移学习?
- 相关数据太少,训练的模型不好
- 训练网络模型时调参花费时间太长
- 训练大型模型的时间所需太多
迁移学习就是将他人已经训练好的要达到类似目标的模型(比如自己想做车的分类,就拿他人车的分类模型)的参数(即权重参数、偏置参数等)拿过来初始化(不用简单的随机初始化了)。
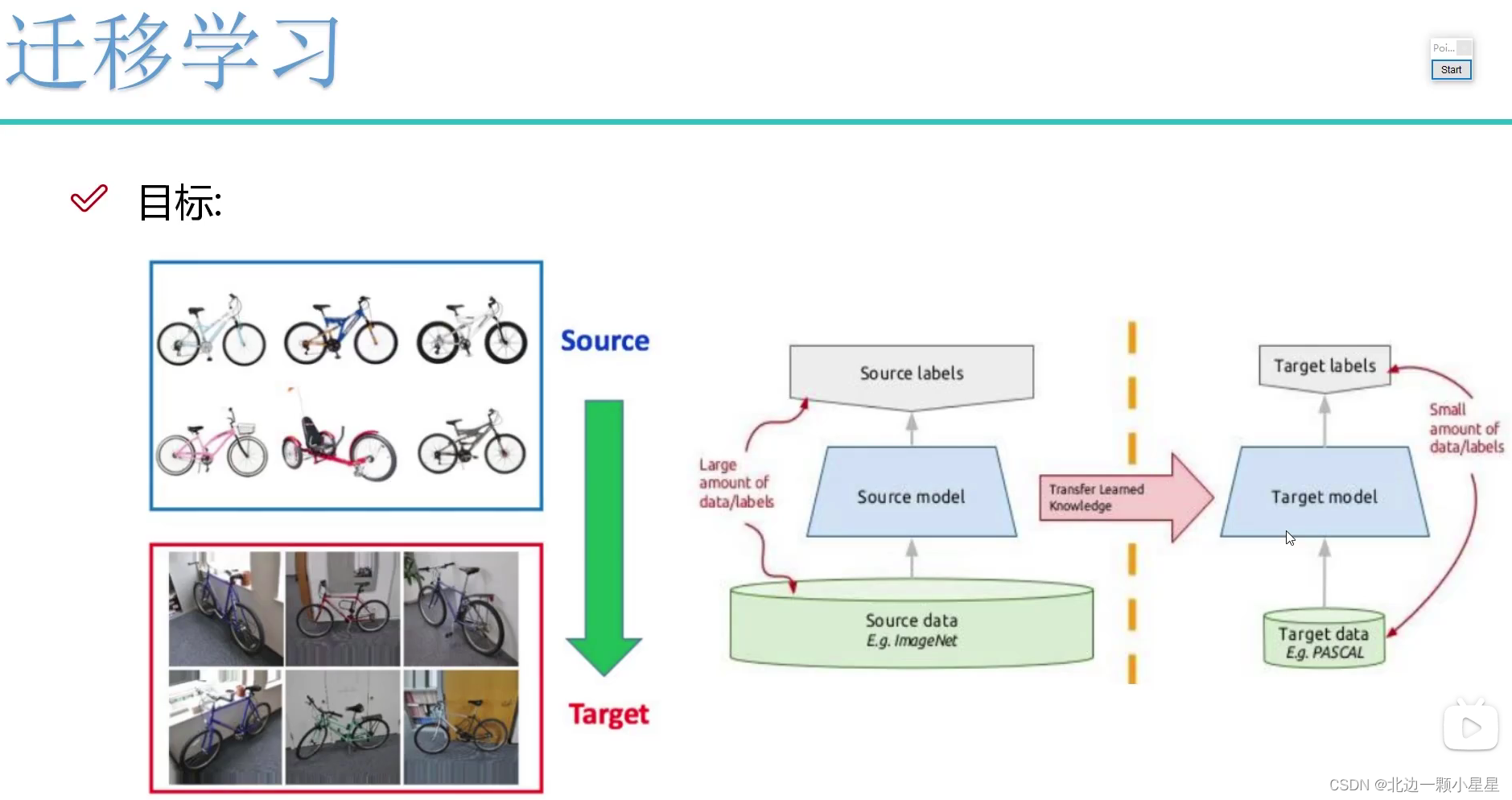
举个例子,
ImageNet
数据集,它有
1000
个不同的类别,因此这个网络会有一个 Softmax
单元,它可以输出
1000
个可能类别之一。
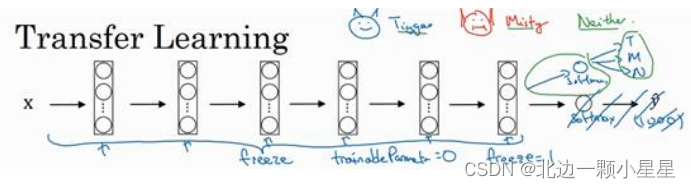
我们可以去掉这个
Softmax
层,创建自己的
Softmax
单元,用来输出
Tigger
、
Misty
和
neither
三个类别。就网络而言,建议把所有的层看作是冻结的,冻结网络中所有层的参数,只需要训练和你的 Softmax
层有关的参数。这个
Softmax
层有三种可能的输出,
Tigger
、
Misty
或者都不是。
通过使用其他人预训练的权重,很可能得到很好的性能,即使只有一个小的数据集。幸运的是,大多数深度学习框架都支持这种操作,事实上,取决于用的框架,它也许会trainableParameter=0 这样的参数,对于这些前面的层,你可能会设置这个参数。为了不训练这些权重,有时也会freeze=1
这样的参数。不同的深度学习编程框架有不同的方式,允许你指定是否训练特定层的权重。在这个例子中,我们只需要训练 softmax
层的权重,把前面这些层的权重都冻结。
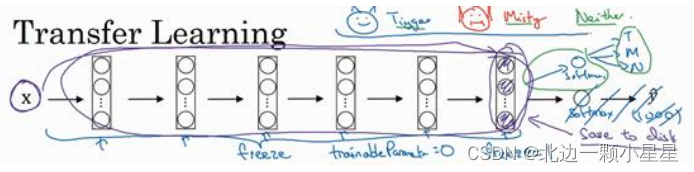
另一个技巧,也许对一些情况有用,由于前面的层都冻结了,相当于一个固定的函数,不需要改变。因为不需要改变它,也不训练它,取输入图像𝑋
,然后把它映射到这层(softmax
的前一层)的激活函数。所以这个能加速训练的技巧就是,如果我们先计算这一层(紫色箭头标记),计算特征或者激活值,然后把它们存到硬盘里。你所做的就是用这个固定的函数,在这个神经网络的前半部分(softmax
层之前的所有层视为一个固定映射),取任意输入图像𝑋
,然后计算它的某个特征向量,这样你训练的就是一个很浅的
softmax
模型,用这个特征向量来做预测。对计算有用的一步就是对自己训练集中所有样本的这一层的激活值进行预计算,然后存储到硬盘里,然后在此之上训练 softmax
分类器。所以,存储到硬盘或者说预计算方法的优点就是,你不需要每次遍历训练集再重新计算这个激活值了。

因此如果任务只有一个很小的数据集,可以这样做。要有一个更大的训练集怎么办呢?根据经验,如果有一个更大的标定的数据集,也许有大量的 Tigger
和
Misty的照片,还有两者都不是的,这种情况,应该冻结更少的层,比如只把这些层冻结,然后训练后面的层。如果输出层的类别不同,那么需要构建自己的输出单元,Tigger
、
Misty
或者两者都不是三个类别。有很多方式可以实现,我们可以取后面几层的权重,用作初始化,然后从这里开始梯度下降。
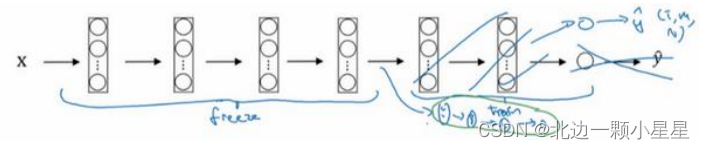
或者可以直接去掉这几层,换成自己的隐藏单元和你自己的
softmax
输出层,这些方法值得一试。但是有一个规律,如果有越来越多的数据,需要冻结的层数越少,能够训练的层数就越多。这个理念就是,如果你有一个更大的数据集,也许有足够多的数据,那么不要单单训练一个 softmax
单元,而是考虑训练中等大小的网络,包含你最终要用的网络的后面几层。

最后,如果有大量数据,我们应该做的就是用开源的网络和它的权重,把这所有的权重当作初始化,然后训练整个网络。再次注意,如果这是一个 1000
节点的
softmax
,而我们只有三个输出,需要自己的 softmax
输出层来输出你要的标签。如果有越多的标定的数据,或者越多的 Tigger
、
Misty 或者两者都不是的图片,可以训练越多的层。极端情况下,我们可以用下载的权重只作为初始化,用它们来代替随机初始化,接着可以用梯度下降训练,更新网络所有层的所有权重。这就是卷积网络训练中的迁移学习。









![[架构之路-200]- 性能需求与性能分析:影响性能的主要因素](https://img-blog.csdnimg.cn/20210928172207220.png?x-oss-process=image/watermark,type_ZHJvaWRzYW5zZmFsbGJhY2s,shadow_50,text_Q1NETiBAZHhtZHhtMTIz,size_20,color_FFFFFF,t_70,g_se,x_16)