C++ 图进阶系列之剖析二分图的染色算法和匈牙利算法

news2024/11/29 12:51:18

1. 前言

二分图又称作二部图或称为偶图，是图论中的一种特殊类型，有广泛的应用场景。

什么是二分图？

  • 二分图一般指无向图。看待问题要有哲学思想，有二分图也可以是有向图。

  • 如果图中所有顶点集合能分成两个独立的子集，且任一子集中的任意顶点之间没有边连接，则称这样的图为二分图。

如下图中的图结构都可称为二分图。

1.png

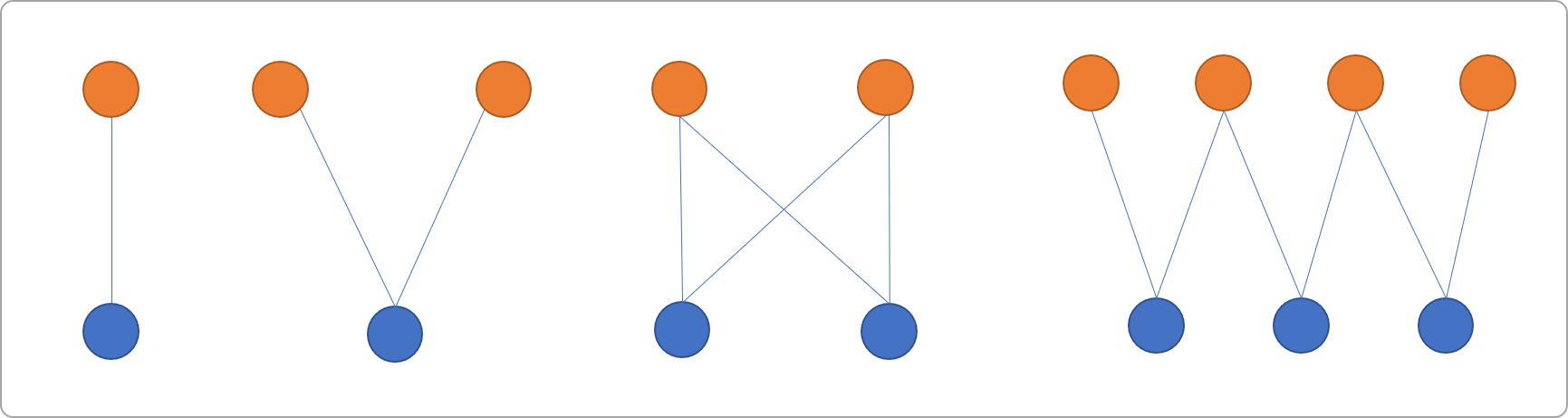
二分图的特点：

  • 理论而言，图中至少有一个环，如果图中无环，则图退化成树。在研究树和图时，一般会把树问题当成图问题的子类。
  • 二分图中不能有奇数个顶点组成的环。

如何验证二分图中的环不能是奇数个顶点？

  • 环也称为回路，指路径的起点和终点为同一顶点。
  • 证明这个问题，可以使用染色算法，此算法是判断二分图的经典算法。

2. 染色算法

二分图的定义已经说明，图中存在二个独立的子集，为了区分这两个子集，可以给其中一个子集中的顶点染上红色，另一个子集中的顶点染上蓝色。具体是什么颜色并不重要，只要能区分就可以。

染色算法本质：

  • 使用DFS或BFS对遍历图，且图中所有顶点染色。
  • 一旦发现有一个顶点与其邻接顶点的颜色相同，可以判定图结构不是二分图。

感观上应该有预知，如果是奇数环，想必会有至少一对邻接顶点颜色相同。

2.1 染色偶数环

如下图结构是否是二分图？

此图结构中有一个环，且构成环的顶点数为偶数。
2.png

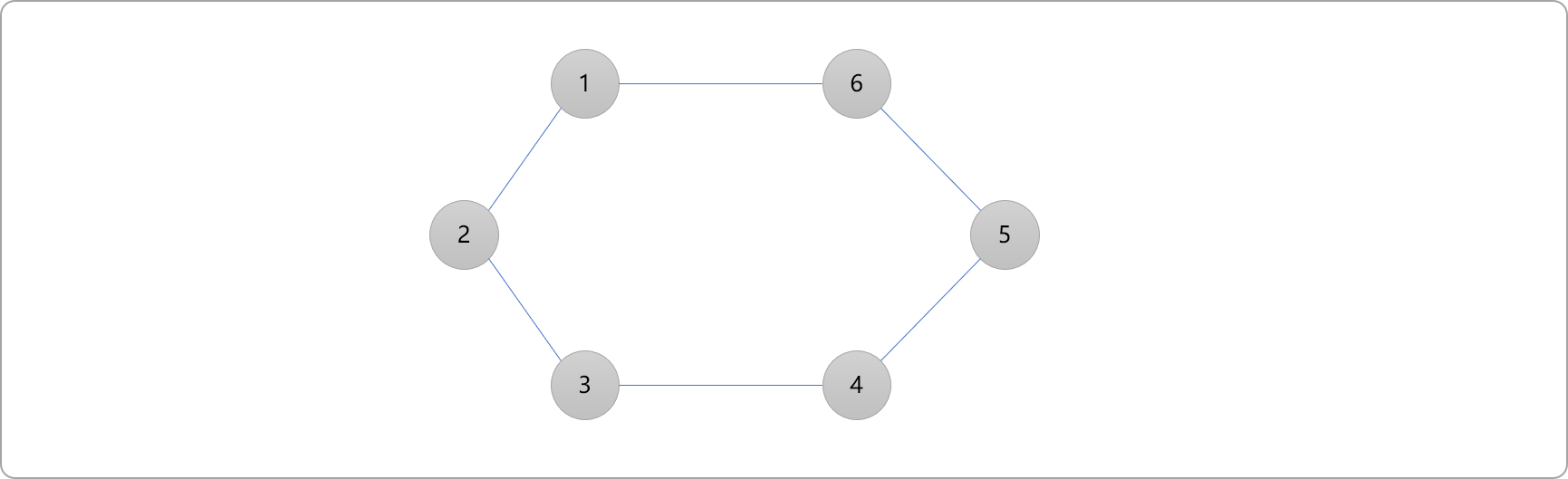
使用染色算法判定的流程如下：

  • 从编号为1的顶点开始，给其染上红色，标记为红色子集中的成员。

3.png

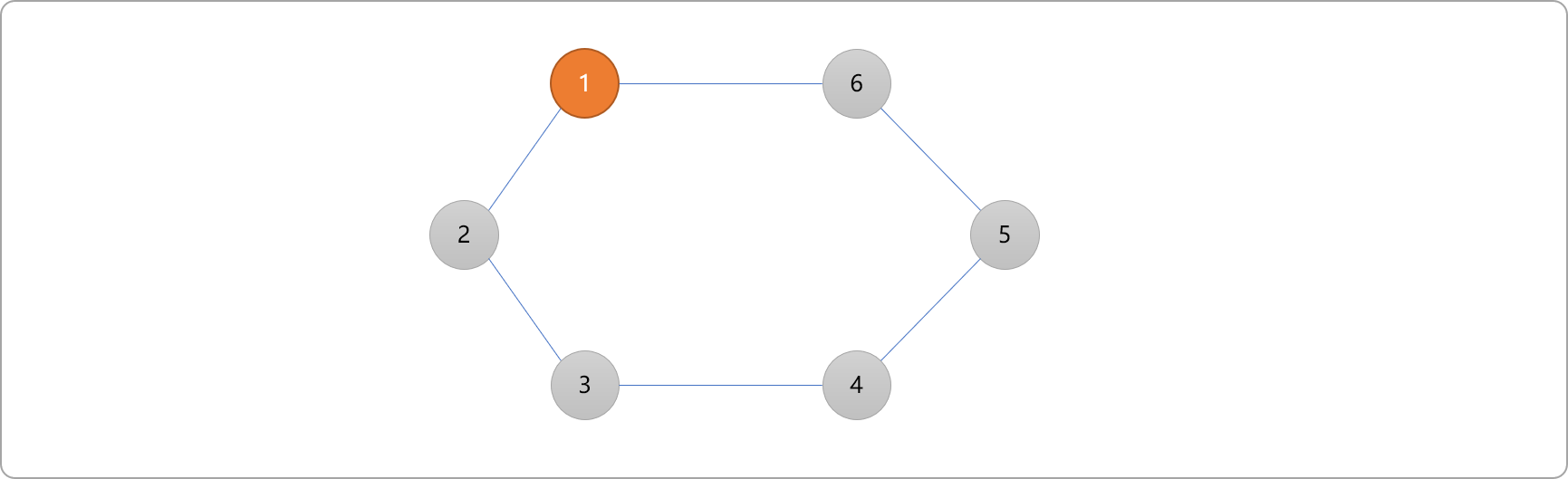
  • 找到编号1的相邻顶点2和6。因同一个子集中的顶点之间不能有边连接。编号为2和6的顶点不可能和编号 为1的顶点为同一个子集，所以编号2和6的顶点只可能存在于另一个子集中，故标记为蓝色。

4.png

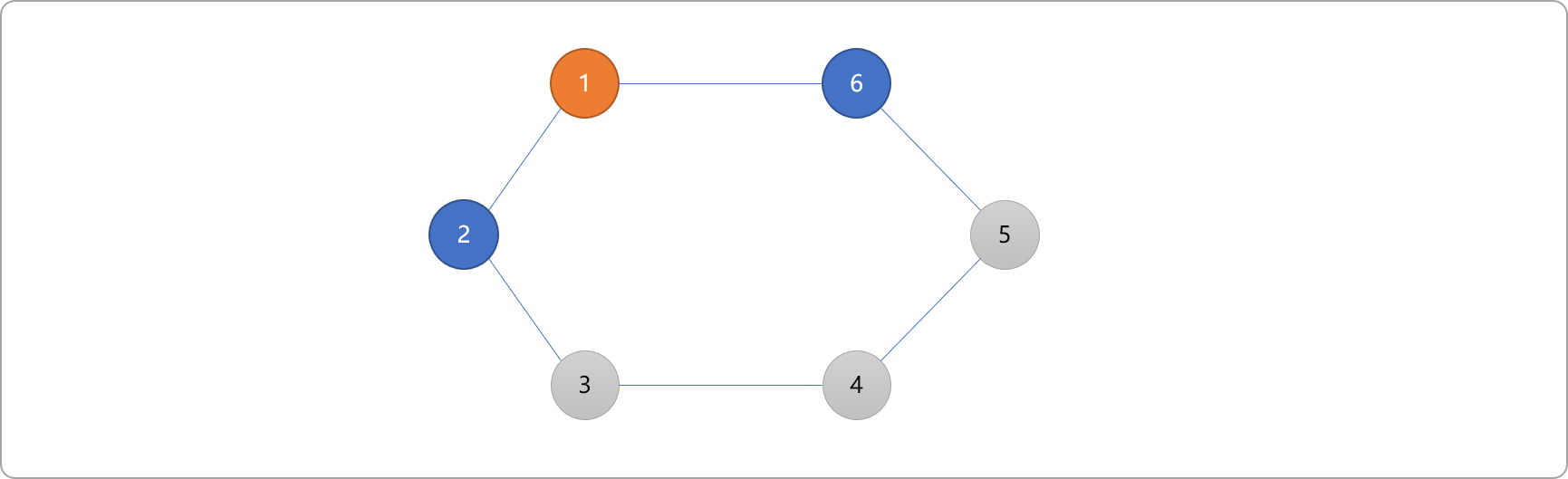
  • 找到与编号2相邻的顶点3，根据二分图的定义，编号为3的顶点只可能染上红色。同理，与编号6相邻的顶点5也只可能染上红色。

5.png

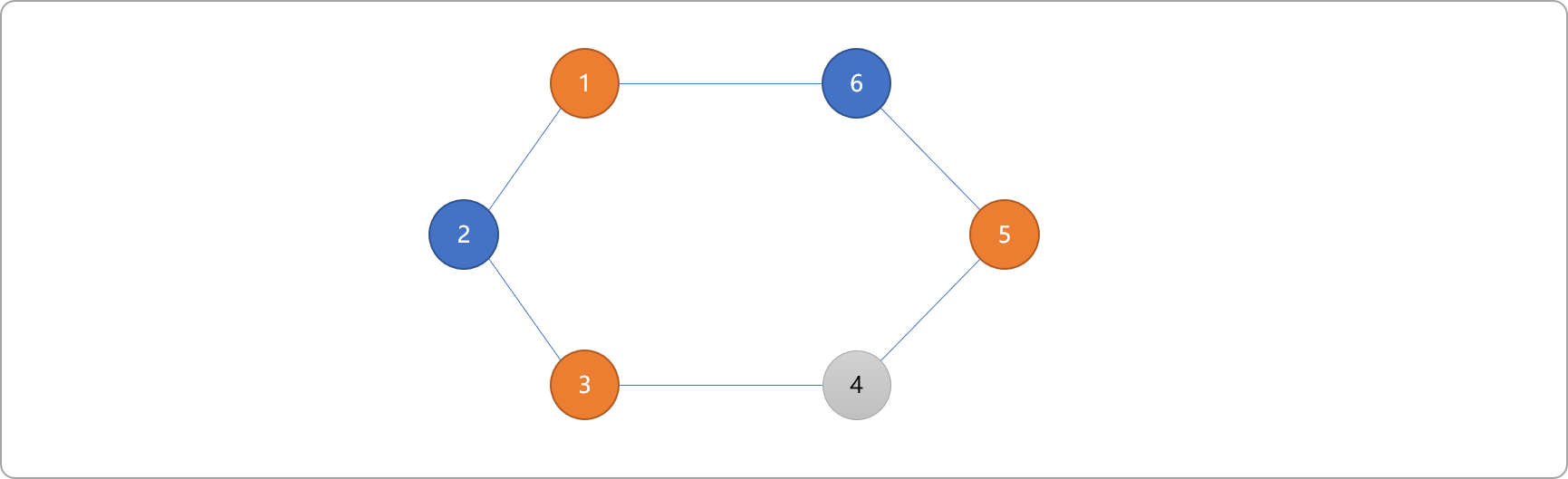
  • 编号为4的顶点是编号为3和5的邻接顶点。显然，只能染上蓝色。

6.png

  • 遍历完所有节点后，每一个节点都染上颜色，且所有边两端的顶点颜色不相同（这是判定成功的依据）。可以判定此图为二分图。对图结构稍微变形一下。

7.png

2.2 染色奇数环

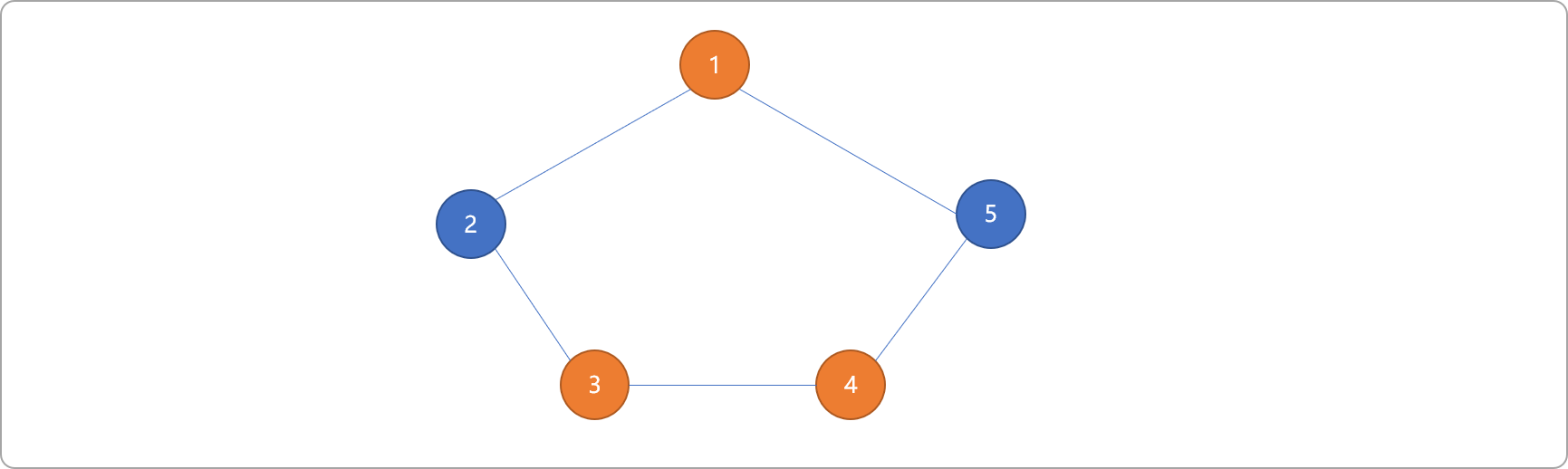
来一个奇数环的图结构，同样使用染色算法判断此图是否为二分图。

8.png

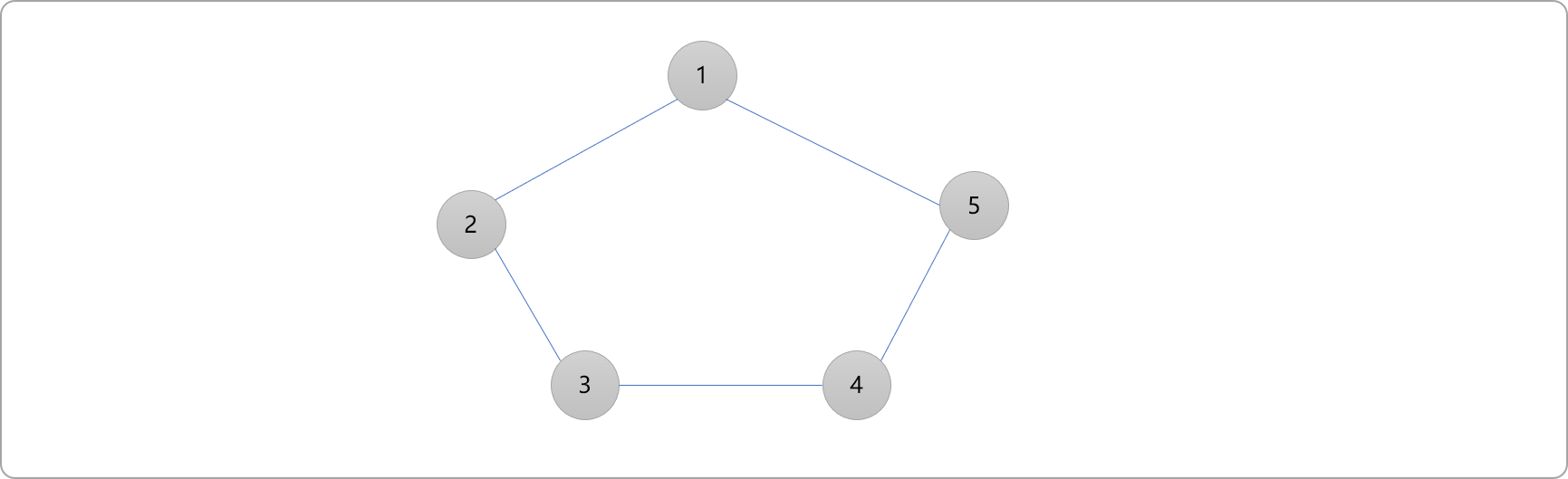
  • 从编号1开始，染色为红色。

9.png

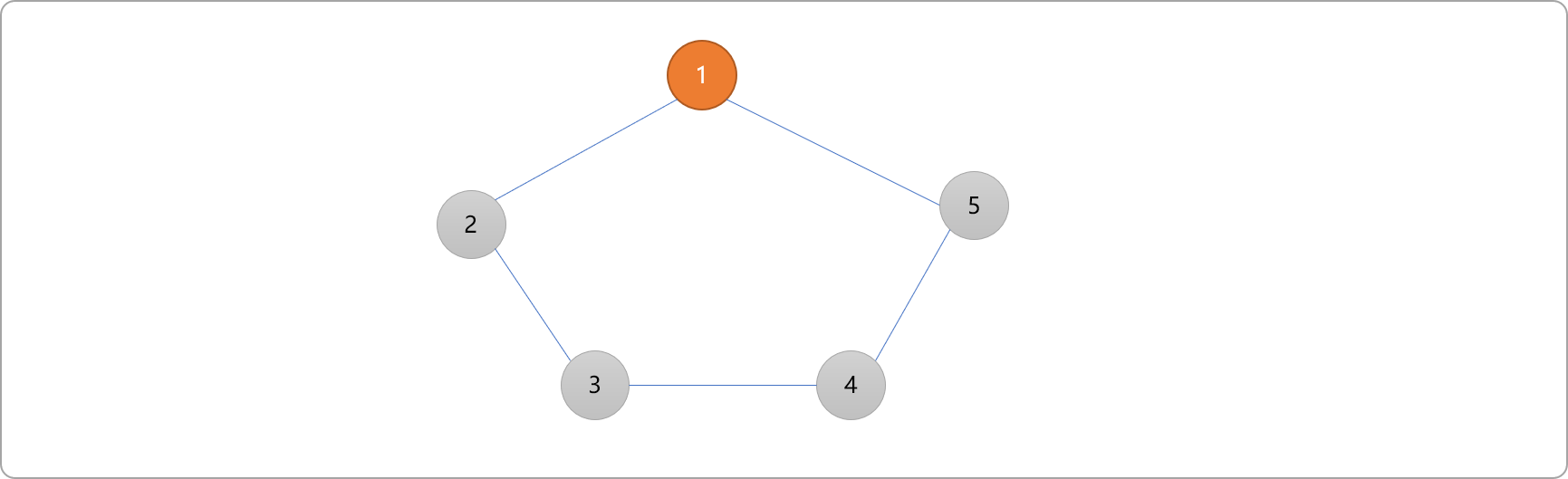
  • 找到编号1的邻接顶点2、5。染色为蓝色。

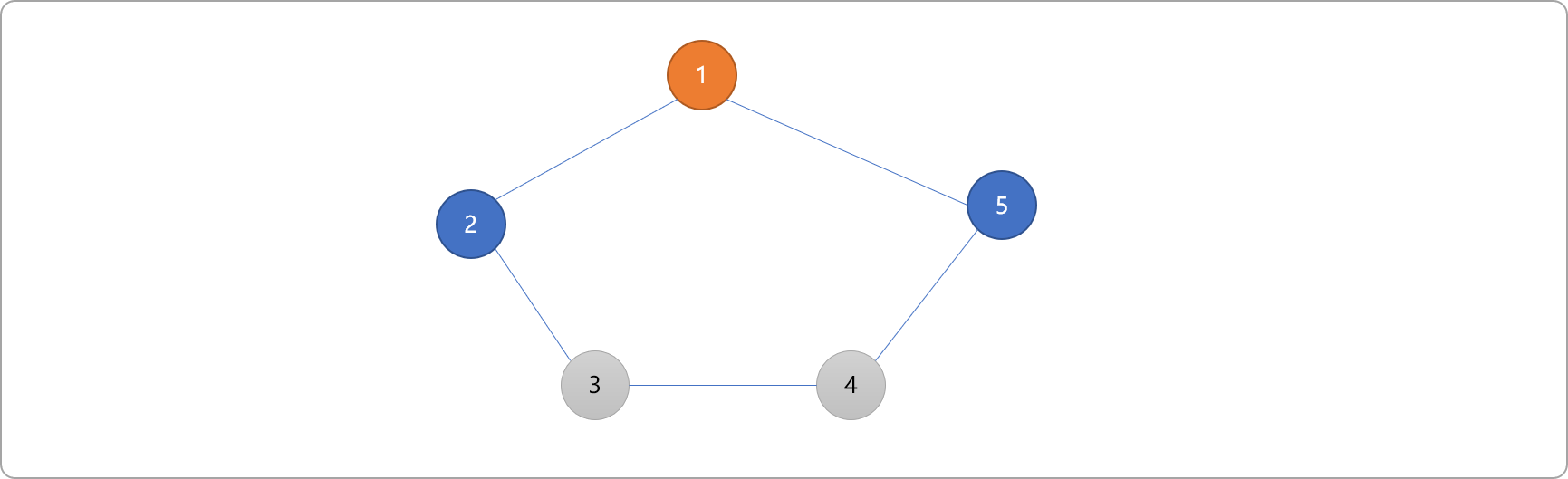
10.png

  • 找到编号2的邻接顶点3，染色为红色。编号5的邻接顶点4，染色为红色。

11.png

  • 编号为3和4的顶点都染上了红色。根据二分图的定义，邻接顶点的颜色不能相同。所以，当环的顶点数量为奇数时，图不具二分性质。

小结一下：

染色算法就是给图中顶点染色：

  • 如果最终所有边两端的颜色不相同，则可认定图为二分图。
  • 如果最终图中只要有一条边两端的颜色相同，则可认定图不是二分图。

2.3 编码实现

如下编码实现中，使用 1表示红色，-1表示蓝色，0表示没有染色。

顶点类型：

#include <iostream>
#include <vector>
using namespace std;
/*
* 顶点类型
*/
struct Vertex {
	//编号
	int vid;
	//数据
	int val;
	//颜色 0：没染色，  1: 红色 -1: 蓝色
	int color;
	//邻接节点
	vector<int> edges;
	Vertex() {
        //默认没有染色
		this->color=0;
	}
	Vertex(int vid,int val,int color  ) {
        //默认没有染色
		this->color=0;
		this->vid=vid;
		this->val=val;
	}
	/*
	*添加邻接顶点
	*/
	void addEdge(int vid) {
		this->edges.push_back(vid);
	}
};

图类： 函数中仅体现核心逻辑，弱化了如验证之类的代码。图的顶点编号从 1开始。

class Graph {
	private:
		//所有顶点
		vector<Vertex*> allVertexs;
		//顶点编号
		int number;
	public:
		Graph() {
			this->number=1;
			//0 位置填充一个占位符。简化操作，顶点的编号值即为其存储位置编号
			this->allVertexs.push_back(NULL);
		}
    
		/*
		*添加顶点,返回顶点的编号。没有检查顶点是否存在
		*/
		int addVertex(int val) {
			//创建新的顶点
			Vertex* ver=new Vertex(number++,val,0);
			this->allVertexs.push_back(ver);
			return ver->vid;
		}
    
		/*
		* 添加邻接边
		*/
		void addEdge(int fromId,int toId) {
			//无向图中顶点间双向关系
			this->allVertexs[fromId]->addEdge(toId);
			this->allVertexs[toId]->addEdge(fromId);
		}

		/*
		* 深度搜索(也可以使用广度搜索)算法对图中的顶点染色
		* 1 :表示红色
		* -1：表示蓝色
		*/
		bool fillColor(int fromId,int color) {
			//当前顶点的颜色
			this->allVertexs[fromId]->color=color;
			//找到所有邻接顶点
			vector<int> vers=this->allVertexs[fromId]->edges;
			for(int i=0; i<vers.size(); i++) {
				if(this->allVertexs[vers[i]]->color!=0) {
					//已经染过颜色
					if( this->allVertexs[vers[i]]->color==color  ) {
						//如果和邻接顶点颜色相同
						return false;
					}
				} else {
					//没染色，深度搜索
					return fillColor(vers[i],-1*color);
				}
			}
			return true;
		}
};

测试代码：

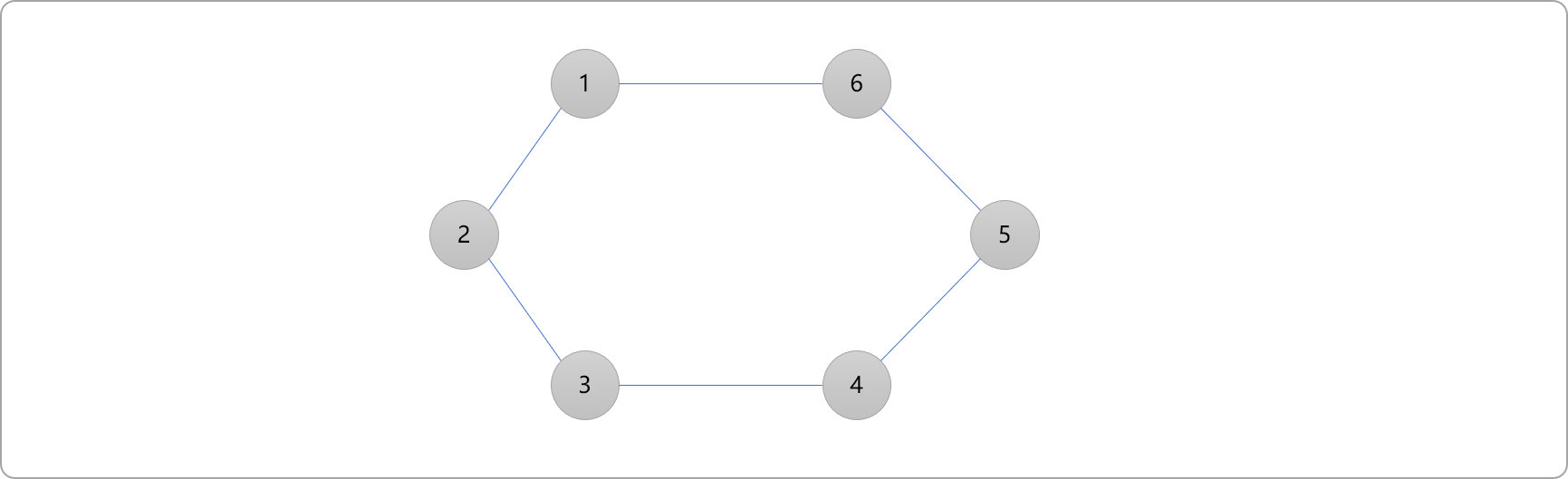
  • 测试下图是否为二分图，环由偶数个顶点构成。

2.png

int main(int argc, char** argv) {
	Graph* graph=new Graph();
	for(int i=1; i<=6; i++)
		graph->addVertex(i);
	graph->addEdge(1,2);
	graph->addEdge(1,6);
	graph->addEdge(2,3);
	graph->addEdge(3,4);
	graph->addEdge(4,5);
	graph->addEdge(5,6);
	string fill=graph->fillColor(1,1)?"是二分图":"不是二分图";
	cout<<fill<<endl;
	return 0;
}

输出结论：

12.png

  • 测试奇数个数的环图。
int main(int argc, char** argv) {
	Graph* graph=new Graph();
	for(int i=1; i<=5; i++)
		graph->addVertex(i);
	graph->addEdge(1,2);
	graph->addEdge(1,5);
	graph->addEdge(2,3);
	graph->addEdge(3,4);
	graph->addEdge(4,5);
	string fill=graph->fillColor(1,1)?"是二分图":"不是二分图";
	cout<<fill<<endl;
	return 0;
}

输出结果：

13.png

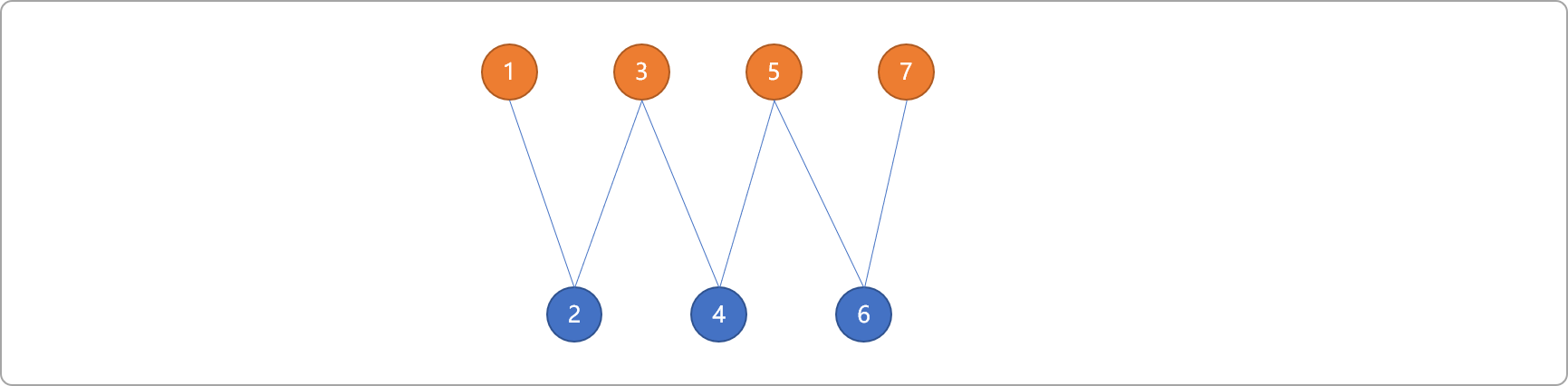
  • 二分图中不一定必须有环结构。
    14.png
int main(int argc, char** argv) {
	Graph* graph=new Graph();
	for(int i=1; i<=7; i++)
		graph->addVertex(i);
	graph->addEdge(1,2);
	graph->addEdge(2,3);
	graph->addEdge(3,4);
	graph->addEdge(4,5);
	graph->addEdge(5,6);
	graph->addEdge(6,7);
	string fill=graph->fillColor(1,1)?"是二分图":"不是二分图";
	cout<<fill<<endl;
	return 0;
}

输出结果：

15.png

3. 二分图最大匹配

3.1 匈牙利算法思想

先了解什么是二分图的最大匹配概念。

二分图把图的顶点分成了两个子集， 如使用 n和m表示。要求选出一些边，所有边中没有公共顶点的边称为匹配边，求最多匹配边的算法为最大匹配算法。

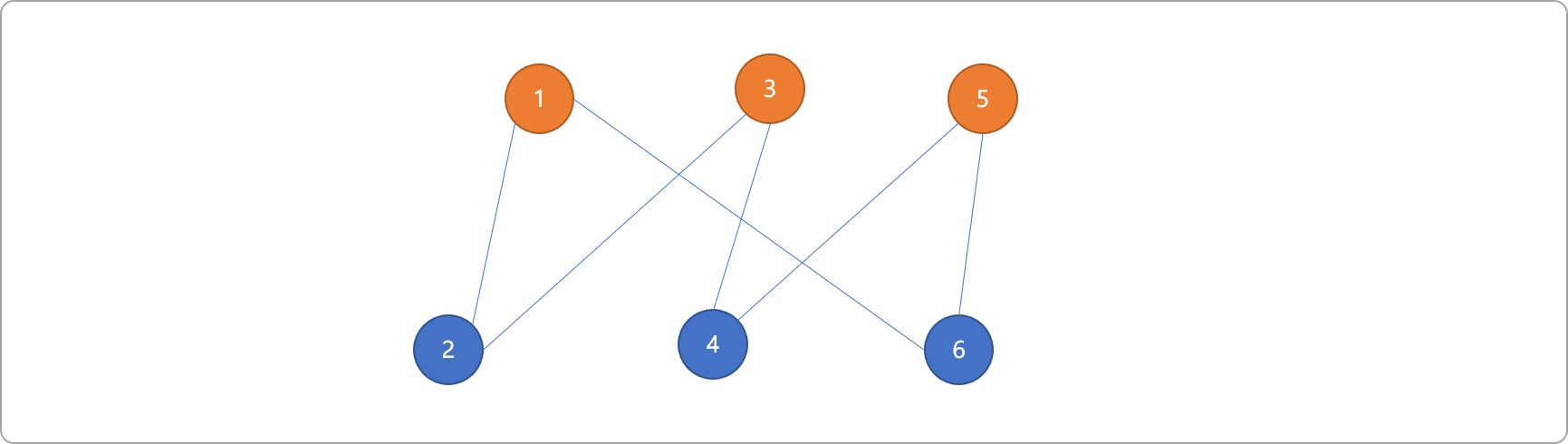
如下图，标记为红色的边为匹配边，蓝色边为不匹配边。且最大匹配数为 3。

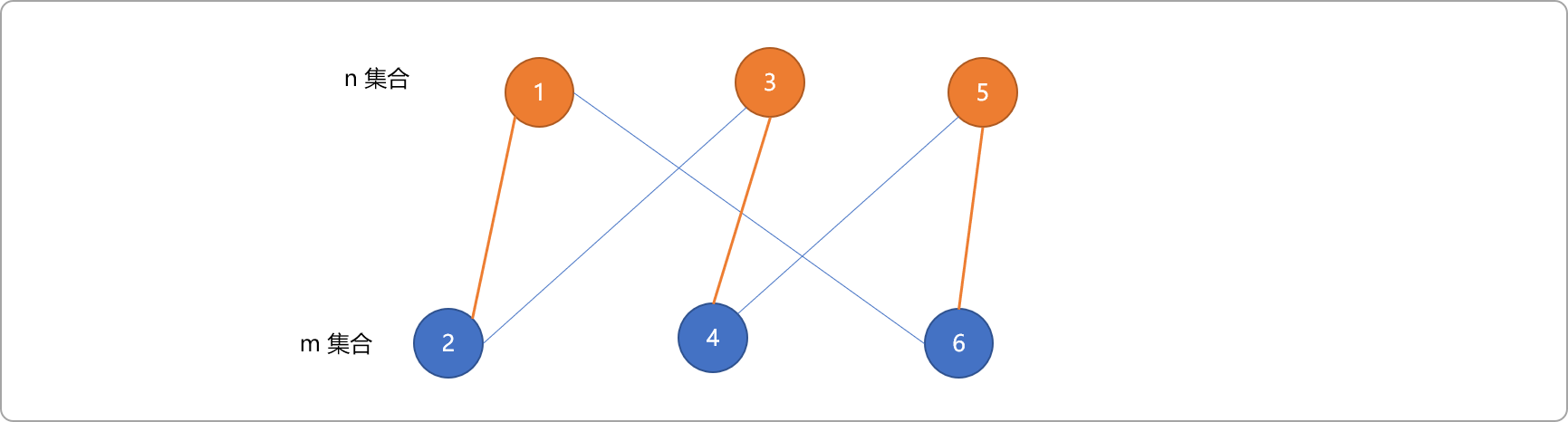
17.png

把n集合当成相亲时的男士群体，m集合当成女士群体。一个男士可以和多个女士有联系，但是，一个男士最终只能迎娶一位女士。即如果集合n和m中的顶点已经被选为匹配边，则这两个顶点与其它顶点连接的边就一定是不匹配边。

求二分图最大匹配边的算法：

  • 用增广路求最大匹配（称作匈牙利算法，匈牙利数学家Edmonds于1965年提出）。
  • 转换成网络流模型。

本文仅讲解匈牙利算法，网络流算法有兴趣者可自行了解。

使用匈牙利算法之前，先要了解两个概念：

  • 交替路：从一个未匹配的点出发，依次经过未匹配边、匹配边、未匹配边…这样的路叫做交替路。
  • 增广路：从一个未匹配的点出发，走交替路，到达了一个未匹配过的点，这条路叫做增广路。

如下图，已知(3.4)和(5,6)为匹配边，3、4、5、6为匹配顶点。

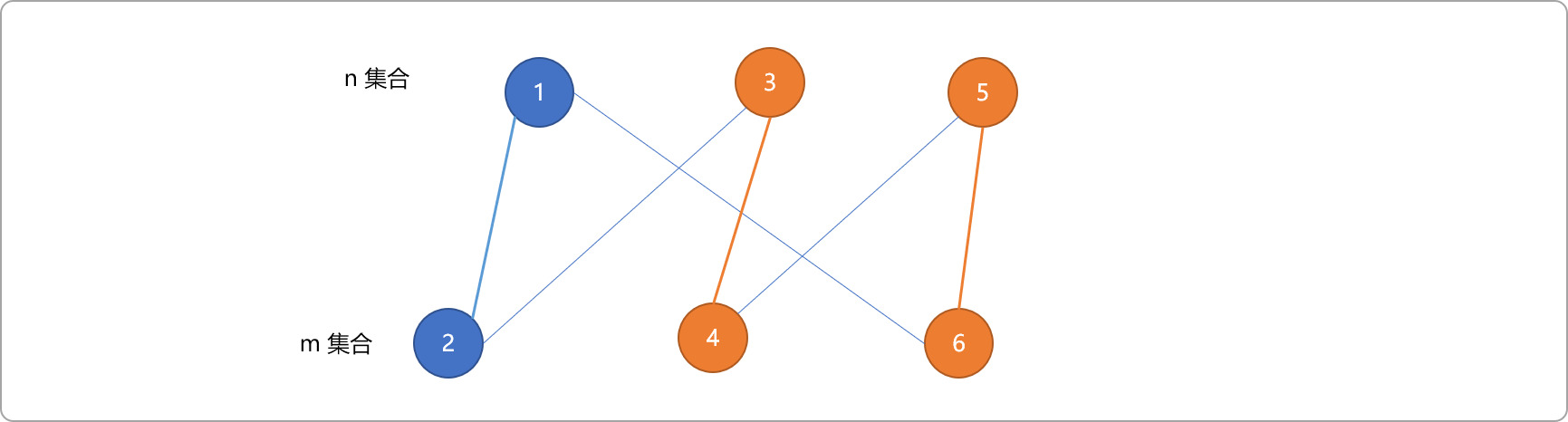
18.png

则，2->3->4->5->6->1便是一条增广路。

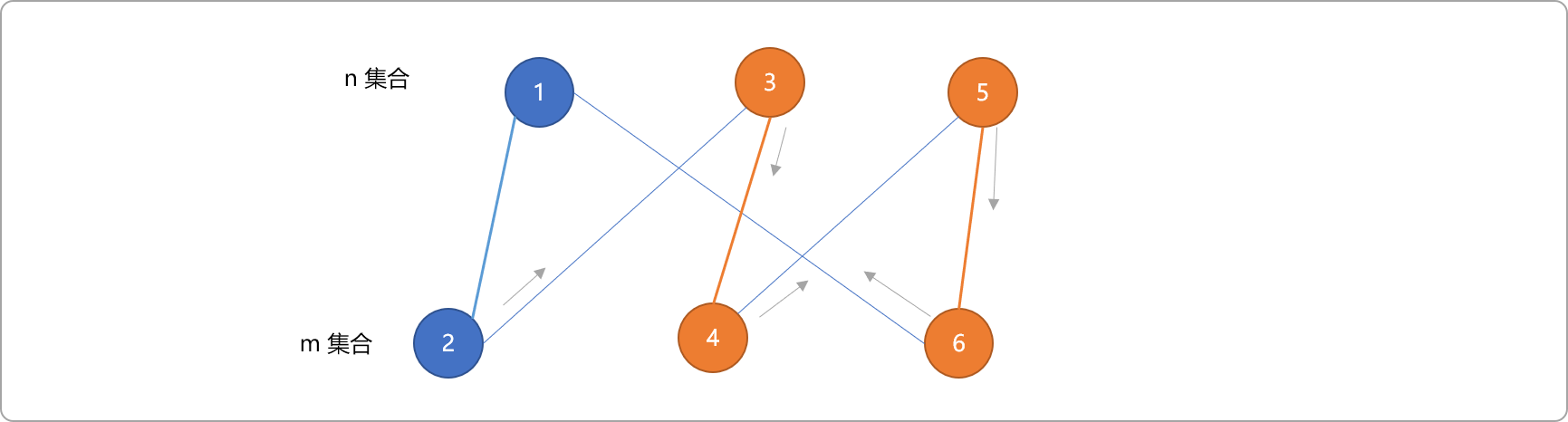
19.png

增广路有如下几个特点：

  • 增广路有奇数条边 。
  • 路径上的点一定分属两个子集。
  • 起点和终点都是目前还没有配对的点。
  • 未匹配边的数量比匹配边的数量多1，这个原由应该很好理解。

匈牙利算法的核心思想：

  • 枚举所有未匹配点，找增广路径。
  • 直到找不到增广路径。

如下描述匈牙利算法的流程：

  • 找出如下图结构的最大匹配。初始所有顶点为非匹配点，所有边为非匹配边。 准备一个数组，存储匹配边。数组下标表示顶点编号，值表示匹配顶点。

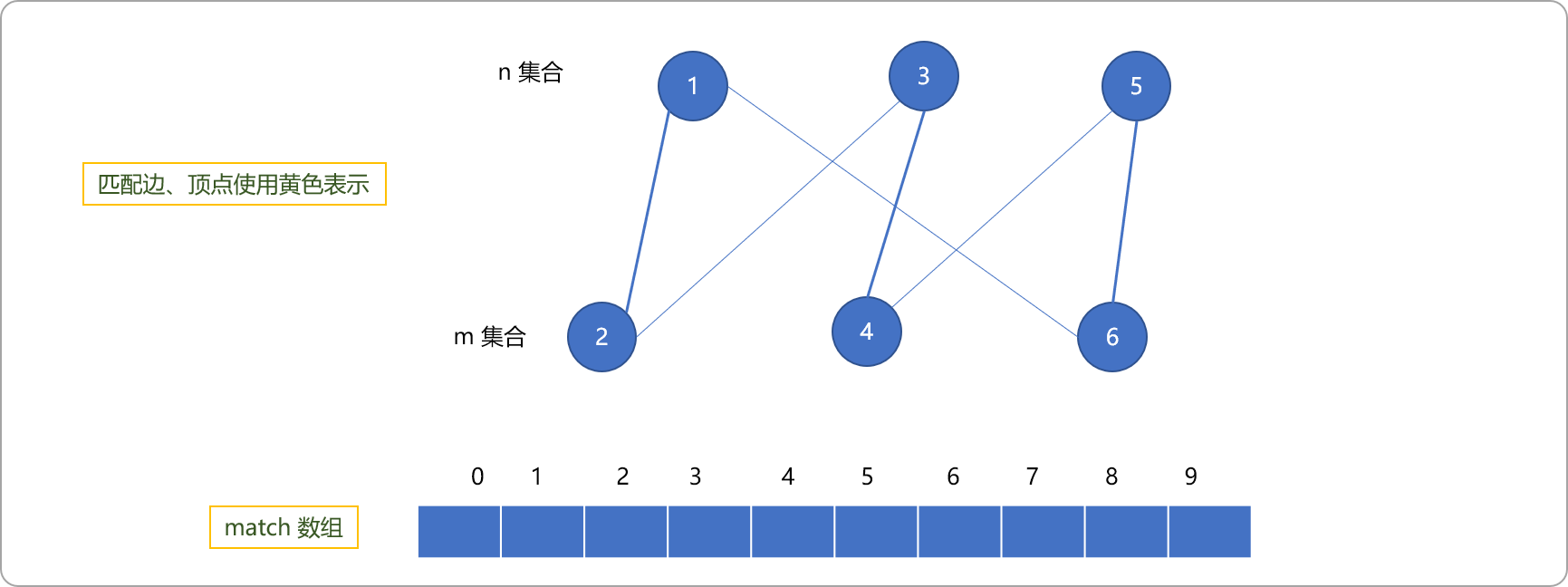
20.png

  • 以编号为1的顶点为出始点，深度搜索查找增广路（终止于非匹配点）。则(1,2)和(1,6)都为有效选择，选择(1,2)。根据增广路的定义，此增广路不能再延长。设置1为匹配点。

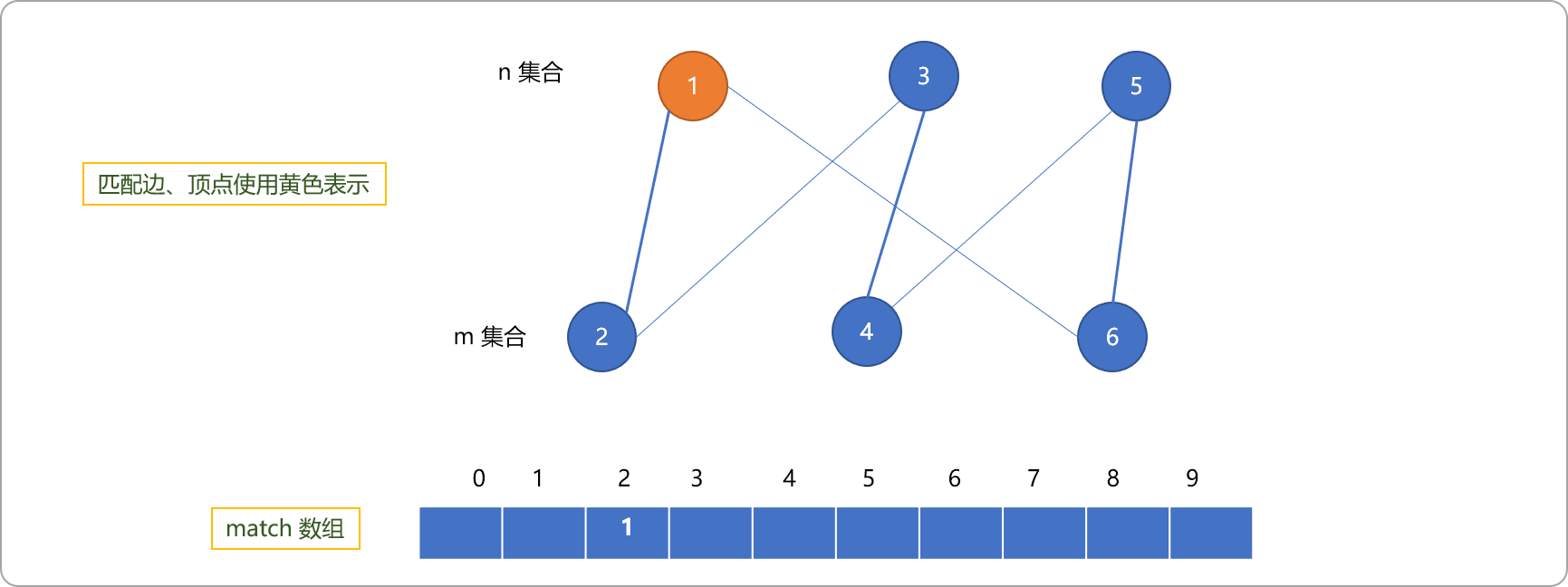
21.png

  • 匈牙利算法的特点是扫描所有顶点，且以每一个顶点为出发点深度搜索查找增广路。

    再从编号为2的顶点出发。如下图所示，2会成为匹配顶点。

    注意，只要图中还存在增广路，现所记录的匹配信息都不是最终结果，这些匹配信息可能会被更新。

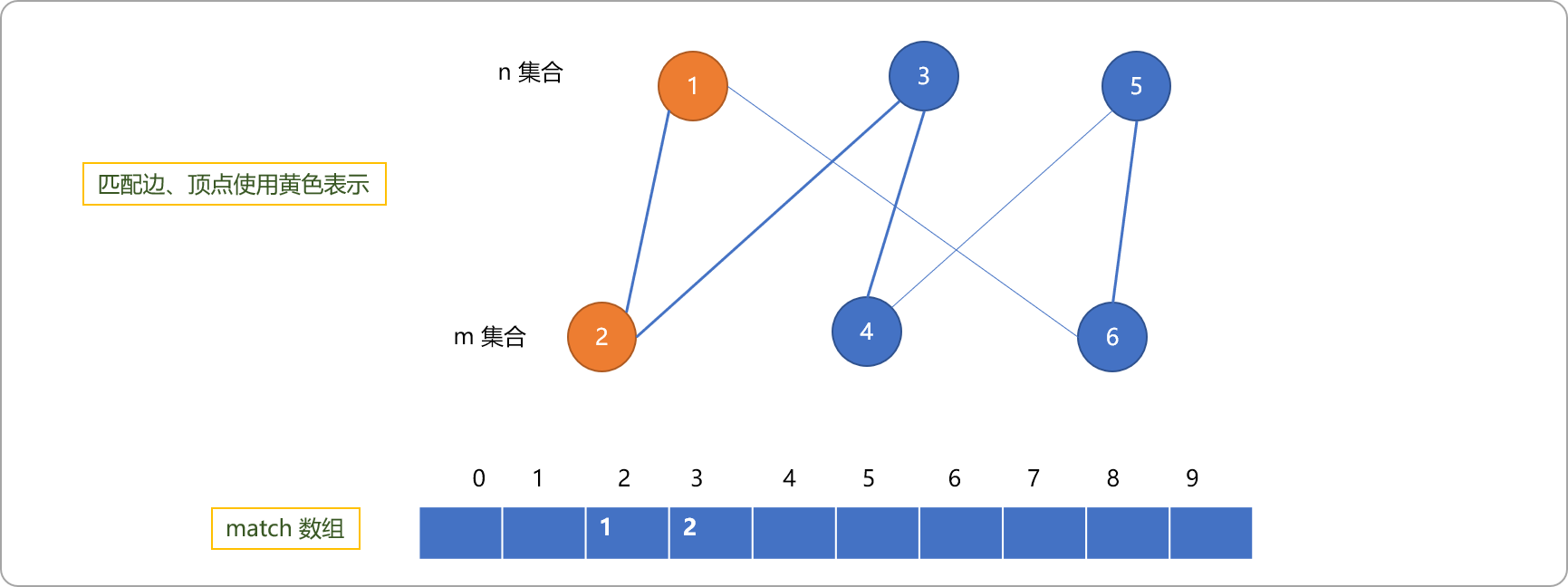
23.png

  • 以顶点3为出发点。以3->2->1->6路径进行搜索，因6是非匹配点，增广路终止于6，设置1为匹配点。

    这里要注意，在递归向上过程中，会修改编号2为3的匹配点。

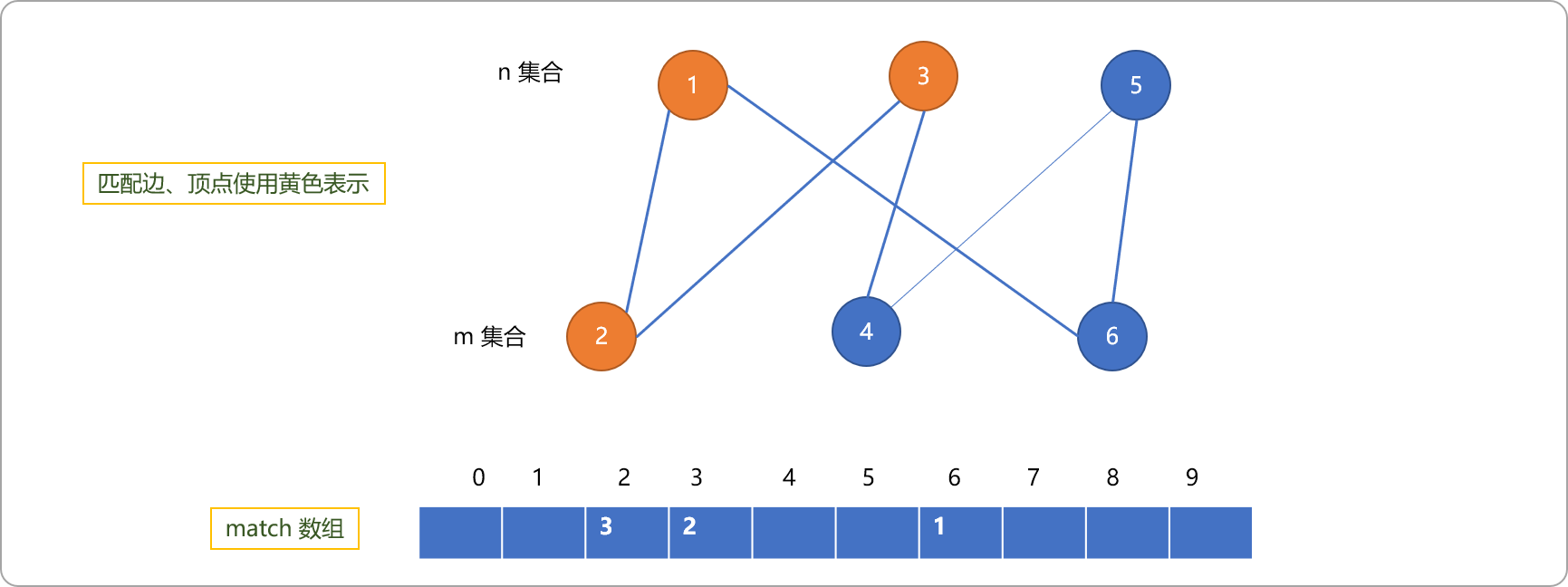
24.png

  • 以编号为 4 的顶点作为出发点。走4->5，因5是非匹配点，设置4为5的匹配点。

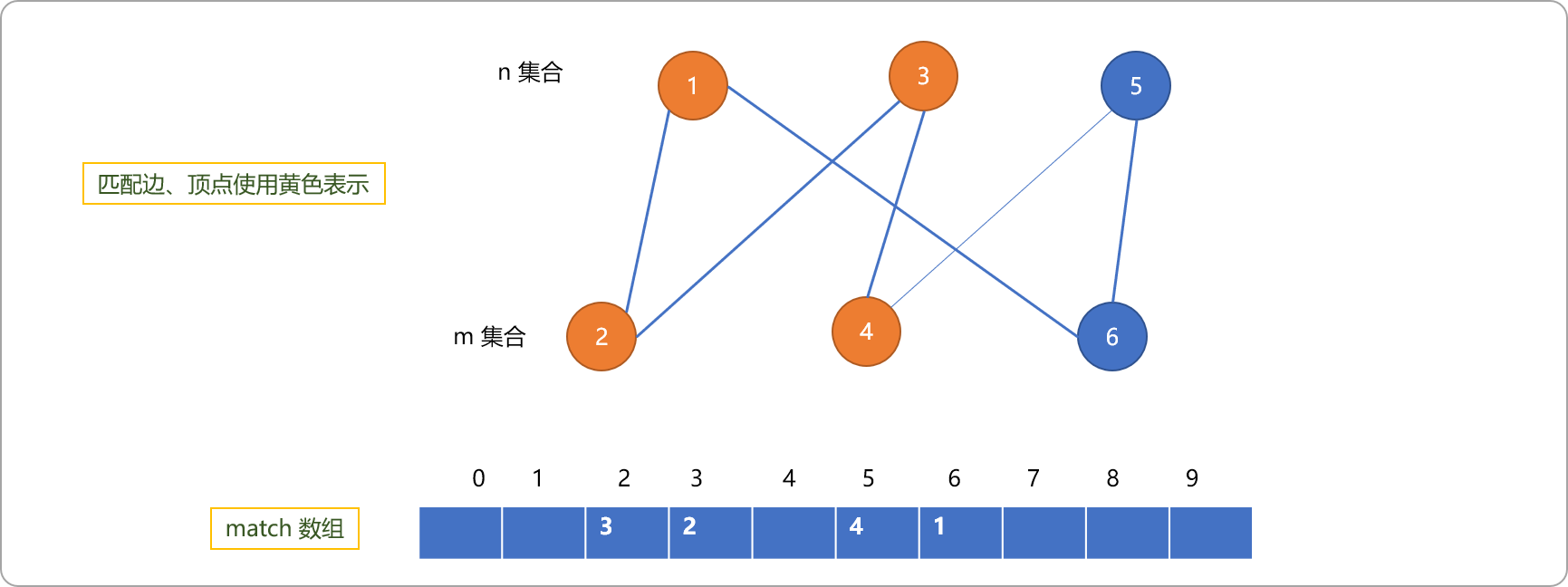
25.png

  • 以编号5为出发点，走5->4路线，置5为4的匹配点。

29.png

  • 以编号为6的顶点出发，设置编号6为1的匹配点。把匹配点之间的边用红色颜色描出来，便是最大匹配边。

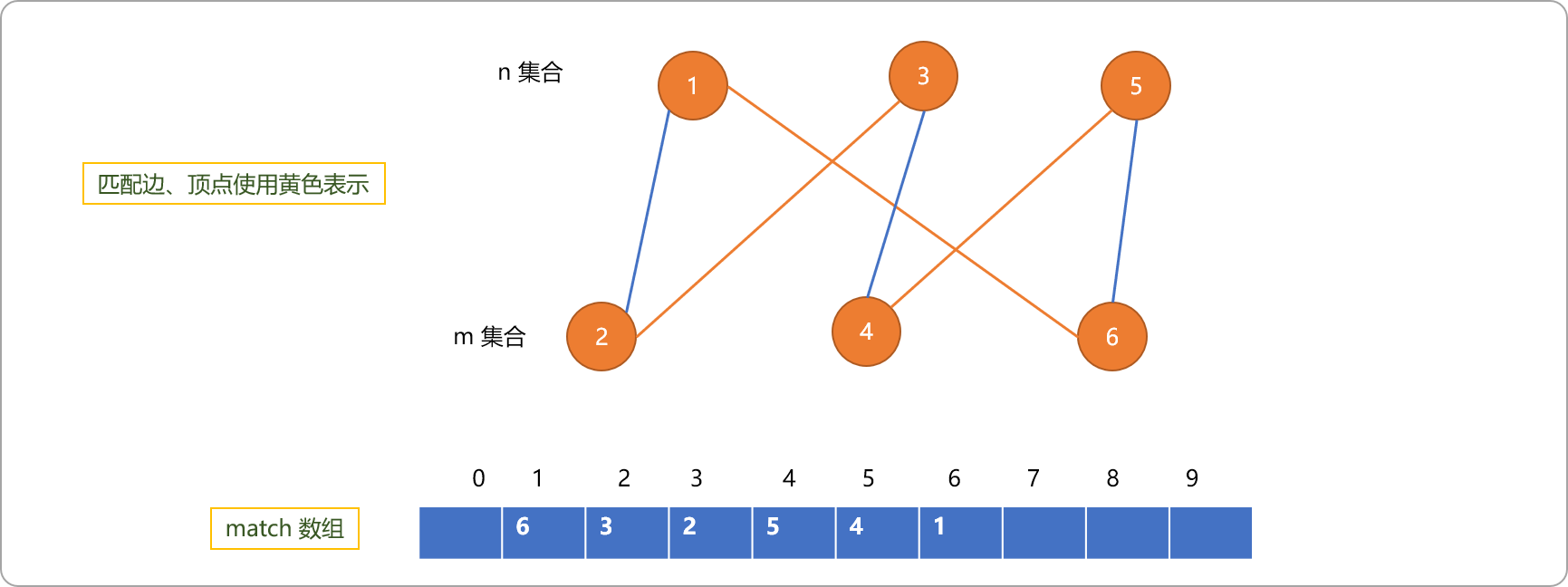
27.png

3.2 编码实现

使用匈牙利算法的前提条件：图必须是二分图。

#include <iostream>
#include <vector>
#include <cstring>
#define maxn 10
using namespace std;

//存储边信息 
vector<int> edges[maxn];
//存储匹配边    
int match[maxn];
//每一次搜索过程中记录顶点状态     
bool vis[maxn];    
int n,m;           
/*
* 深度搜索查找增广路 
*/ 
bool dfs(int x) {
	for(int i=0; i<edges[x].size(); i++) {
		//子节点 
		int v = edges[x][i];
		if(vis[v] == false) {
		    //避免重复访问      
			vis[v] = true;
			/*
			* 1、 如果是非匹配点，直接匹配
			* 2、 否则，继续深度搜索 
			*/ 
			if(match[v] == -1 || dfs(match[v])) {     
				match[v] = x;
				return true;
			}
		}
	}
	return false;
}
int find() {
	n=6;
	m=6;
	edges[1].push_back(2);
	edges[1].push_back(6);
	edges[2].push_back(3);
	edges[2].push_back(1);
	edges[3].push_back(2);
	edges[3].push_back(4);
	edges[4].push_back(5);
	edges[4].push_back(3);
	edges[5].push_back(4);
	edges[5].push_back(6);
	edges[6].push_back(1);
	edges[6].push_back(5);

	int sum = 0;
	memset(match,-1,sizeof(match));

	for(int i=1; i<=n; i++) {
		memset(vis,false,sizeof(vis));     
		if(dfs(i)) sum ++;
	}
	return sum;
}

int main() {
	int res= find();
	cout<<res<<endl;
	for(int i=1;i<=n;i++){
		cout<<match[i]<<"\t";
	}
	return 0;
}

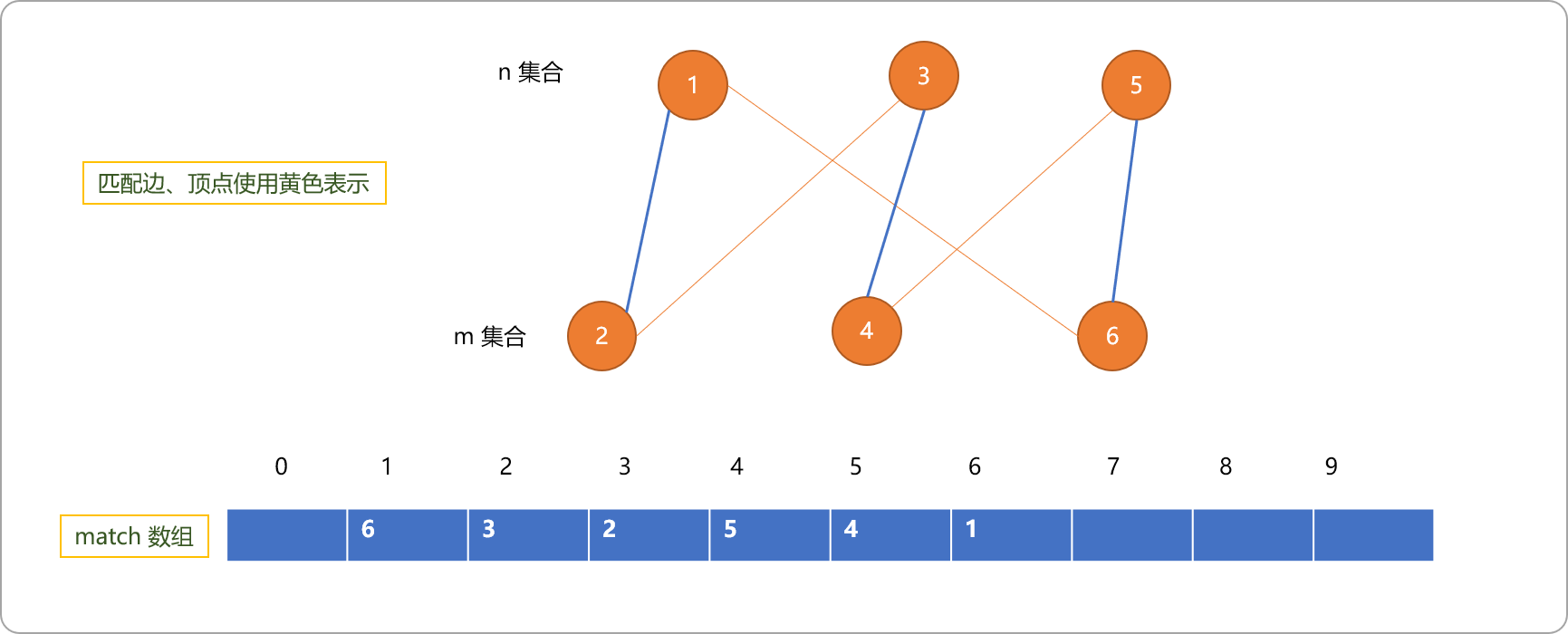
执行代码后，match数组中的内容如下图所示：

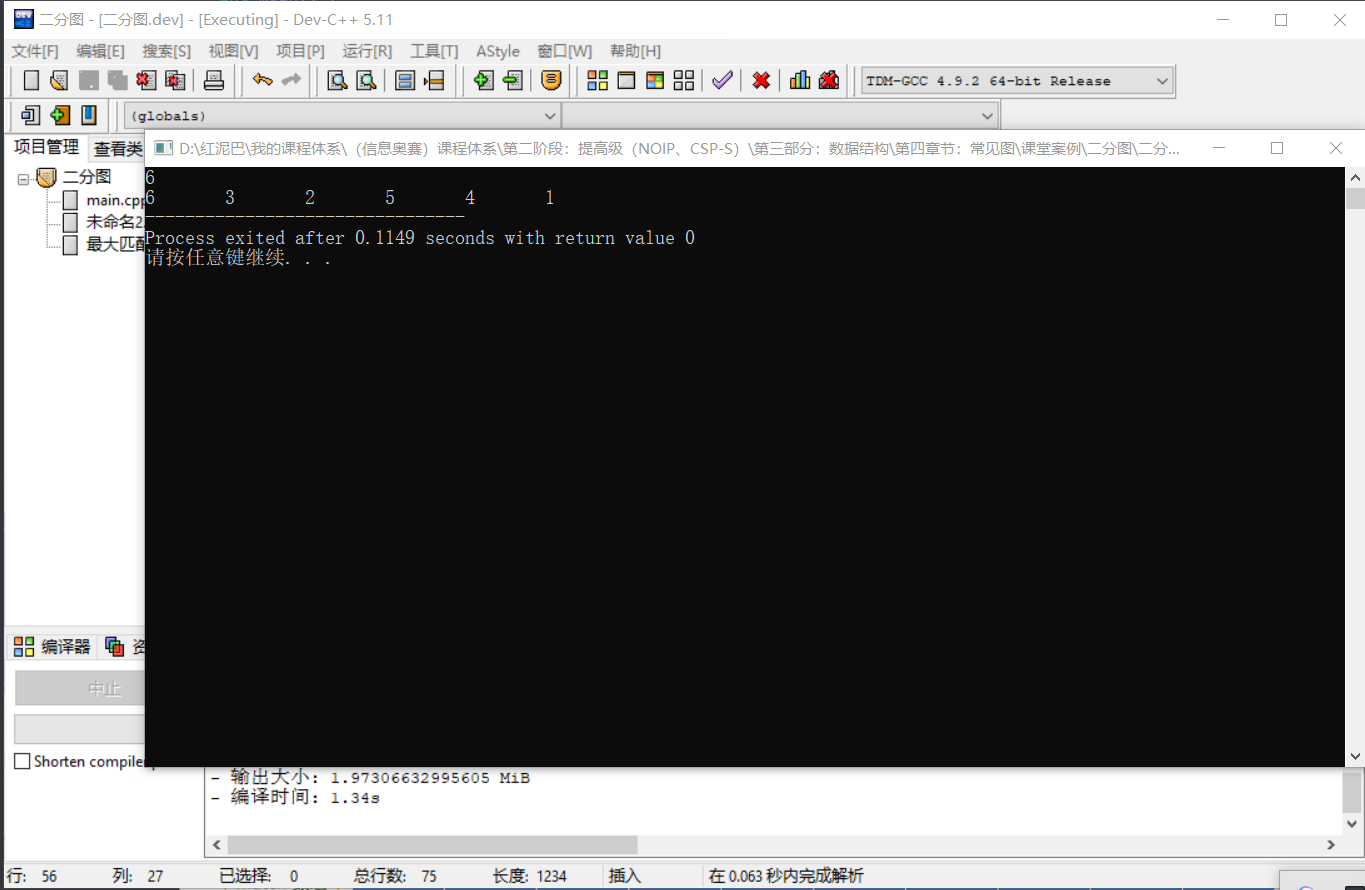
28.png

数组中是双向记录，实际最大匹配边只有 3 条。

26.png

4. 总结

本文讲解了二分图的定义以及如何使用染色算法判定图是否为二分图。且讲解了求解最大匹配边的匈牙利算法。

本质上都是基于深度搜索实现的。

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/532765.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

常用好用的远程连接工具分享

常用好用的远程连接工具分享

1、RayLink 介绍&#xff1a; RayLink它是一款功能强大的远程控制软件&#xff0c;支持Windows、macOS、IOS以及Android等多种操作系统。同时&#xff0c;它还提供了手机端和桌面端两种不同的应用程序&#xff0c;可以通过手机控制电脑&#xff0c;也可以通过电脑控制手机。这…
阅读更多...
C语言编程软件

C语言编程软件

C语言是一门历史很长的编程语言&#xff0c;其编译器和开发工具也多种多样&#xff0c;其开发工具包括编译器&#xff0c;现举几个开发工具供大家选择&#xff0c;当然也要根据自己的操作系统来选择适合自己的开发工具。 好多刚开始接触c语言的朋友都想知道用上面软件开发c语言…
阅读更多...
【JavaScript数据结构与算法】字符串类（计算二进制子串）

【JavaScript数据结构与算法】字符串类（计算二进制子串）

个人简介 &#x1f440;个人主页&#xff1a; 前端杂货铺 &#x1f64b;‍♂️学习方向&#xff1a; 主攻前端方向&#xff0c;也会涉及到服务端&#xff08;Node.js&#xff09; &#x1f4c3;个人状态&#xff1a; 在校大学生一枚&#xff0c;已拿多个前端 offer&#xff08;…
阅读更多...
Grafana之Graph Panel使用(05)

Grafana之Graph Panel使用(05)

Graph是Grafana的原生插件。使用Graph Panel，可以将数据展示成折线、条状、点状等风格。Graph是Grafana展示数据的缺省图形面板，它提供了一组非常丰富的绘图选项。 ① Panel options(面板选项)主要包括：Title(标题)；Description(描述) ②Tooltip(鼠标经过图例展示数据效果)…
阅读更多...
数字产品在教育行业的应用：关键特点和必备功能概览

数字产品在教育行业的应用：关键特点和必备功能概览

数字化转型的浪潮已经席卷了各行各业&#xff0c;不仅出现在互联网、电商、建筑等行业&#xff0c;还应用在了教育行业。数字化的教育ERP软件能够在满足学校需求的基础上&#xff0c;帮助学校完善各类工作流程&#xff0c;提高工作效率。 对于一个拥有多个校区&#xff0c;上万…
阅读更多...
LAY-EXCEL实现导入和导出excel功能

LAY-EXCEL实现导入和导出excel功能

lay-excel 是一款开源的、基于 Google Sheets 的免费的在线数据表格库。它使用了 Google Sheets 的开源代码&#xff0c;并进行了本地化处理&#xff0c;以适应中国用户的使用习惯。 lay-excel 提供了丰富的数据表格类型&#xff0c;包括常见的表格、表格拆分、表格计算、图表等…
阅读更多...
JAVA并发专题（1）之操作系统底层工作的整体认识

JAVA并发专题（1）之操作系统底层工作的整体认识

一、分诺依曼计算机模型 现代计算机模型是基于-冯诺依曼计算机模型&#xff0c;计算机在运行时&#xff0c;先从内存中取出第一条指令&#xff0c;通过控制器的译码&#xff0c;按指令的要求&#xff0c;从存储器中取出数据进行指定的运算和逻辑操作等加工&#xff0c;然后再按…
阅读更多...
irq_domain 负责的事情以及小组成员分担的任务

irq_domain 负责的事情以及小组成员分担的任务

文章目录 简介irq_domain 要做哪些事irq_desc 结构图irq_domain 小组的重要成员有哪些irq_domain 小组的重要成员解析irq_domain 的左膀右臂 irq_chip & irq_domain_opsirq_chip 分担了哪些工作irq_domain_ops 分担了哪些工作 其他成员分担了哪些工作 irq_desc 怎么与 irq …
阅读更多...
小程序技术助力智慧家居生态互联

小程序技术助力智慧家居生态互联

随着科技的不断发展&#xff0c;智能终端设备已经成为人们生活中不可或缺的一部分。不仅可以通过智能手机、平板电脑等设备方便地获取信息和进行沟通&#xff0c;现在还可以通过智能电视、智能冰箱等终端设备运行小程序&#xff0c;为人们提供更加便捷的生活体验。 智能终端设…
阅读更多...
C1 计算机系统概论

C1 计算机系统概论

目录 计算机系统简介 计算机的基本组成 计算机硬件的主要技术指标 计算机系统简介 计算机的基本组成 运算器控制器->中央处理器CPU 输入设备输出设备->I/O设备 运算器&#xff1a;ALU 三个寄存器ACC、X、MQ控制器&#xff1a;CU 两个寄存器IR、PC主存储器&#x…
阅读更多...
解决css背景图覆盖文字

解决css背景图覆盖文字

项目需求&#xff1a;这是个导航栏&#xff08;下面是uveiw的tabs标签&#xff09;&#xff0c;然后高亮的时候会有一个背景图&#xff0c;因为title不固定字数&#xff0c;所以宽度不能写死。 想要的效果 做出来的效果 自己写了个样式&#xff0c;用scroll-view&#xff0…
阅读更多...
10分钟西门子SMART200PLC轻松实现连接自建MQTT云平台操作教程

10分钟西门子SMART200PLC轻松实现连接自建MQTT云平台操作教程

目录 一. 使用流程 二. 准备工作 2.1 需要准备如下物品 2.2 LF220网关准备工作 2.3 PLC准备工作 2.4 电脑的准备工作 2.5 MQTT服务器 三. MQTT网关登陆平台配置步骤 3.1 登录 3.2 网关概况 3.3 MQTT连接配置 3.4 驱动管理 3.5 变量管理 四. MQTT客户…
阅读更多...
全网首次公开，阿里巴巴新产Java性能优化小册（2023版），理论实战起飞

全网首次公开，阿里巴巴新产Java性能优化小册（2023版），理论实战起飞

性能优化可以说是很多一线大厂对其公司内高级开发的基本要求&#xff08;其中以Java岗最为显著&#xff09;。其原因有两个&#xff1a;一是提高系统的性能&#xff0c;二是为公司节省资源。两者都能做到&#xff0c;那你就不可谓不是普通程序员眼中的“调优大神了”。 那么如…
阅读更多...
pyqt5界面+myql+跳绳系统设计

pyqt5界面+myql+跳绳系统设计

pyqt5界面myql跳绳系统设计 改项目主要是学习界面的设计开发&#xff0c;已把一些流行的算法做成功能较好的系统&#xff0c;这里以跳绳计数算法为例子&#xff0c;进行一个开发流程。 跳绳计数算法 1.基于Mediapipe&#xff08;本文使用0.8的版本&#xff09;进行人体骨架关…
阅读更多...
yolo v8

yolo v8

这个系列代码被封装的非常的精致&#xff0c;对二次开发不太友好&#xff0c;虽然也还是可以做些调节 模型的导出 有三种方式试过&#xff0c;都可以导出onnx的模型 1. 用yolov8 源码来自&#xff1a;ultralytics\yolo\engine\exporter.py (不固定尺寸) yolo export modelpa…
阅读更多...
Unity HybridCLR 热更工具学习日记（一）

Unity HybridCLR 热更工具学习日记（一）

目录 导入HybridCLR包、安装设置相关选项 导入HybridCLR包 先找到HybridCLR包的git地址&#xff1a;https://github.com/focus-creative-games/hybridclr 复制包的http地址&#xff0c;打开unity - window - package Manager&#xff1b;点击左上角的 选择Add Package for…
阅读更多...
Ch4.字符串

Ch4.字符串

文章目录 4.字符串KMP算法next数组nextval数组 （优化后的next数组）4.字符串 1.串： 串是一种特殊的线性表，数据直接呈线性关系 2.字符集编码 3.串的存储 (1)顺序存储 ①静态数组 ②动态数组 王道教材采用静态数组 (2)链式存储 4.字符串模式匹配 (1)概念
阅读更多...
7.免交互

7.免交互

文章目录 Here Document免交互Expect例子 Here Document免交互 Here Document 免交互 使用I/O重定向的方式将命令列表提供给交互式程序或命令&#xff0c;比如ftp、 cat或read命令。是标准输入的一种替代品&#xff0c;可以帮助脚本开发人员不必使用临时文件来构建输入信息&a…
阅读更多...
深度学习笔记2——CNN识别手写数字

深度学习笔记2——CNN识别手写数字

深度学习笔记2——CNN识别手写数字 本文将介绍LeNet-5和MNIST手写数字识别的PyTorch实现案例。 参考文献&#xff1a;《Gradient-Based Learning Applied to Document Recognition》数据集&#xff08;MNIST&#xff09;&#xff1a;THE MNIST DATABASE完整代码&#xff08;G…
阅读更多...
ChatGPT接入微信公众号（手把手教学）

ChatGPT接入微信公众号（手把手教学）

前言 本篇文章参考国内服务器 3 分钟将 ChatGPT 接入微信公众号&#xff08;超详细&#xff09;配置&#xff0c;纠正了一些过时的信息。 准备 一个微信公众号 一个能访问外网的梯子 一个ChatGPT账号 有了这些就可以配置了 注册免费服务器&#xff0c;并部署代码 前往Laf…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023