深度学习笔记2——CNN识别手写数字
本文将介绍LeNet-5和MNIST手写数字识别的PyTorch实现案例。
- 参考文献:《Gradient-Based Learning Applied to Document Recognition》
- 数据集(MNIST):THE MNIST DATABASE
- 完整代码(Github):MNIST_LeNet-5_PyTorch.py
手写数字数据集(MNIST)
在深度学习中,常用的实验手写数据集为28x28的MNIST黑白手写数字数据集,由60000张训练+10000张测试图片组成,示例图片如下:

原始数据集文件下载解压后是由4个ubyte文件组成,如下:
| 文件名 | 文件大小 | 注释 |
|---|---|---|
| t10k-images-idx3-ubyte | 7,657KB | 测试10000张图片矩阵数据 |
| t10k-labels-idx1-ubyte | 10KB | 测试10000张图片对应标签数据 |
| train-images-idx3-ubyte | 45,938KB | 训练60000张图片矩阵数据 |
| train-labels-idx1-ubyte | 59KB | 训练60000张图片对应标签数据 |
可以引入struct.unpack()读取这些ubyte文件,需要注意的是头部的魔法数字,读取函数和案例如下:
import struct
import numpy as np
def load_byte(file, cache='>IIII', dtp=np.uint8):
"""
读取 ubyte 格式数据
Args:
file (str): 文件路径的字符串
cache (str): 缓存字符
dtp (type): 矩阵类型
Returns:
np.array
"""
iter_num = cache.count('I') * 4
with open(file, 'rb') as f:
magic = struct.unpack(cache, f.read(iter_num))
data = np.fromfile(f, dtype=dtp)
return data
# 读取出来的均是Numpy矩阵,可以通过dtype指定矩阵类型
train_data = load_byte("train-images-idx3-ubyte") # shape(47040000,)
test_data = load_byte("t10k-images-idx3-ubyte") # shape(60000,)
train_label = load_byte("train-labels-idx1-ubyte", ">II") # shape(7840000,)
test_label = load_byte("t10k-labels-idx1-ubyte", ">II") # shape(10000,)
卷积神经网络(Convolution Neural Network)
卷积神经网络,是Yann Lecun等人于1998年投稿的《Gradient-Based Learning Applied to Document Recognition》中首次提出使用卷积神经网络识别32x32手写数字黑白图像,其网络结构名称为LeNet-5。
网络中采用了Conv2D卷积+Subsampliing下采样的组合提取图像特征,最后采用MLP(Multi-Layer Perceptrons)多层感知机的形式将输入特征映射到输出的10个类中,整体结构如下图:
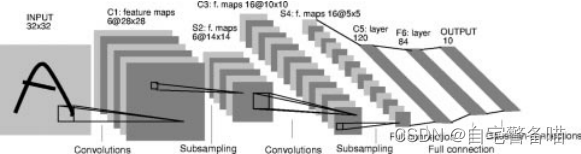
在PyTorch框架中,可以采用MaxPool2d代替Subsampling实现下采样操作,即Conv2d+MaxPool2d的组合。由于文中提出的模型结构输入图片是32x32,而MNIST数据集图片是28x28,因此需要对第一个Conv2d卷积层进行调整,输入通道为1,添加一个padding,使得后续的输出能够适应LeNet-5结构输出,搭建PyTorch代码如下:
import torch
import torch.nn as nn
import torchsummary
class Net(nn.Module):
""" CNN 卷积网络在 MNIST 28x28 手写数字灰色图像上应用版本 """
def __init__(self):
super(Net, self).__init__()
# 卷积层 #
self.conv1 = nn.Conv2d(in_channels=1, out_channels=6, # 输入通道由 3 调整为 1
kernel_size=5, stride=1, padding=2) # padding 使得模型与原文提供的 32x32 结构保持不变
self.conv2 = nn.Conv2d(in_channels=6, out_channels=16,
kernel_size=5, stride=1)
# 池化层 #
self.pool1 = nn.MaxPool2d(kernel_size=2, stride=2)
self.pool2 = nn.MaxPool2d(kernel_size=2, stride=2)
# 全连接层 #
self.fc1 = nn.Linear(16 * 5 * 5, 120)
self.fc2 = nn.Linear(120, 84)
self.fc3 = nn.Linear(84, 10)
# 激活函数 #
self.relu = nn.ReLU()
def forward(self, x):
# 卷积层 1 #
out = self.conv1(x)
out = self.relu(out)
out = self.pool1(out)
# 卷积层 2 #
out = self.conv2(out)
out = self.relu(out)
out = self.pool2(out)
# 全连接层 #
out = out.view(out.size(0), -1)
out = self.fc1(out)
out = self.relu(out)
out = self.fc2(out)
out = self.relu(out)
out = self.fc3(out)
return out
model = Net()
torchsummary.summary(net, input_size=(1, 28, 28), device="cpu") # 采用 keras 的方式顺序打印模型结构
可以调用torchsummary输出keras风格的模型结构表:
----------------------------------------------------------------
Layer (type) Output Shape Param #
================================================================
Conv2d-1 [-1, 6, 28, 28] 156
ReLU-2 [-1, 6, 28, 28] 0
MaxPool2d-3 [-1, 6, 14, 14] 0
Conv2d-4 [-1, 16, 10, 10] 2,416
ReLU-5 [-1, 16, 10, 10] 0
MaxPool2d-6 [-1, 16, 5, 5] 0
Linear-7 [-1, 120] 48,120
ReLU-8 [-1, 120] 0
Linear-9 [-1, 84] 10,164
ReLU-10 [-1, 84] 0
Linear-11 [-1, 10] 850
================================================================
Total params: 61,706
Trainable params: 61,706
Non-trainable params: 0
----------------------------------------------------------------
Input size (MB): 0.00
Forward/backward pass size (MB): 0.11
Params size (MB): 0.24
Estimated Total Size (MB): 0.35
----------------------------------------------------------------
构造数据集
在PyTorch中,训练过程需要使用到torch.utils.data.DataLoader构造的数据迭代器进行模型训练,DataLoader传入的是torch.utils.data.Dataset对象,因此采用torchvision.dataset的MNIST构建数据集对象,代码如下:
from torchvision import transforms
from torchvision.datasets import MNIST
bs = 64 # batch_size
transform = transforms.Compose([
transforms.ToTensor(), # 转换为张量
])
# 构建数据集对象
train_data = MNIST(root=".", train=True, transform=transform)
test_data = MNIST(root=".", train=False, transform=transform)
# 构建数据迭代器
train_db = DataLoader(train_data, batch_size=bs)
test_db = DataLoader(test_data, batch_size=bs)
# 查看单个案例
for (x, y) in train_db:
print(x.shape, y.shape)
break
torch.Size([64, 1, 28, 28]) torch.Size([64])
传入的路径中,需要包含MNIST\raw目录,该目录下包含上述的四个解压后ubyte文件。
训练、验证、测试模型
采用keras进度条的风格的tqdm进度条,在每次epoch训练结束后进行模型验证,部分代码如下:
net = Net() # 初始化模型并加载到GPU
net.to(device)
torchsummary.summary(net, input_size=(num_channels, image_size, image_size)) # 采用 keras 的方式顺序打印模型结构
'''+++++++++++++++++++++++
@@@ 模型训练和验证
+++++++++++++++++++++++'''
criterion = nn.CrossEntropyLoss() # 设置损失函数
optimizer = torch.optim.Adam(net.parameters()) # 配置优化器
# 初始化损失和准确率
train_history = {"loss": {"train": [[] for _ in range(epochs)], "val": [[] for _ in range(epochs)]},
"acc": {"train": [[] for _ in range(epochs)], "val": [[] for _ in range(epochs)]}}
st = time.time()
for epoch in range(epochs):
with tqdm(total=len(train_db), desc=f'Epoch {epoch + 1}/{epochs}') as pbar:
for step, (x, y) in enumerate(train_db):
net.train() # 标记模型开始训练,此时权重可变
x, y = x.to(device), y.to(device) # 转移张量至 GPU
output = net(x) # 将 x 送进模型进行推导
# 计算损失
loss = criterion(output, y) # 计算交叉熵损失
optimizer.zero_grad() # 清空梯度
loss.backward() # 反向传播
optimizer.step() # 一步随机梯度下降算法
# 计算准确率
prediction = torch.softmax(output, dim=1).argmax(dim=1) # 将预测值转换成标签
# 记录损失和准确率
train_history["loss"]["train"][epoch].append(loss.item())
train_history["acc"]["train"][epoch].append(((prediction == y).sum() / y.shape[0]).item())
# 进度条状态更新
pbar.update(1)
pbar.set_postfix({"loss": "%.4f" % np.mean(train_history["loss"]["train"][epoch]),
"acc": "%.2f%%" % (np.mean(train_history["acc"]["train"][epoch]) * 100)})
# 每一个 epoch 训练结束后进行验证
net.eval() # 标记模型开始验证,此时权重不可变
for x, y in val_db:
x, y = x.to(device), y.to(device)
output = net(x)
loss_val = criterion(output, y).item() / len(val_db)
prediction = torch.softmax(output, dim=1).argmax(dim=-1)
# 记录验证损失和准确率
train_history["loss"]["val"][epoch].append(loss_val)
train_history["acc"]["val"][epoch].append(((prediction == y).sum() / y.shape[0]).item())
# 更新进度条
pbar.set_postfix({"loss": "%.4f" % np.mean(train_history["loss"]["train"][epoch]),
"acc": "%.2f%%" % (np.mean(train_history["acc"]["train"][epoch]) * 100),
'val_loss': "%.4f" % np.mean(train_history["loss"]["val"][epoch]),
"val_acc": "%.2f%%" % (np.mean(train_history["acc"]["val"][epoch]) * 100)})
et = time.time()
time.sleep(0.1)
print('Time Taken: %d seconds' % (et - st)) # 69
'''+++++++++++++++++++
@@@ 模型测试
+++++++++++++++++++'''
print('Test data in model...')
correct, total, loss = 0, 0, 0
per_time = [] # 计算每个
net.eval()
with tqdm(total=len(test_db)) as pbar:
for step, (x, y) in enumerate(test_db):
x, y = x.to(device), y.to(device)
st = time.perf_counter()
output = net(x)
torch.cuda.synchronize()
et = time.perf_counter()
per_time.append(et - st)
loss += float(criterion(output, y)) / len(test_db)
prediction = torch.softmax(output, dim=1).argmax(dim=1)
correct += int((prediction == y).sum())
total += y.shape[0]
pbar.update(1)
pbar.set_postfix({'loss': '%.4f' % loss,
'accuracy': '%.2f%%' % (correct / total * 100),
'per_time': '%.4fs' % (et - st)})
print('Time Per-Image Taken: %f seconds' % np.mean(per_time)) # 0.000984
print('FPS: %f' % (1.0 / (np.sum(per_time) / len(per_time)))) # 1015.759509
训练过程中命令行窗口将输出以下进度条记录形式:
Epoch 1/20: 100%|██████████| 94/94 [00:03<00:00, 26.21it/s, loss=1.0145, acc=68.89%, val_loss=0.0165, val_acc=88.14%]
Epoch 2/20: 100%|██████████| 94/94 [00:03<00:00, 27.80it/s, loss=0.2832, acc=91.37%, val_loss=0.0095, val_acc=93.23%]
Epoch 3/20: 100%|██████████| 94/94 [00:03<00:00, 28.02it/s, loss=0.1792, acc=94.60%, val_loss=0.0064, val_acc=95.41%]
Epoch 4/20: 100%|██████████| 94/94 [00:03<00:00, 27.47it/s, loss=0.1261, acc=96.10%, val_loss=0.0051, val_acc=96.21%]
Epoch 5/20: 100%|██████████| 94/94 [00:03<00:00, 26.54it/s, loss=0.0972, acc=96.99%, val_loss=0.0042, val_acc=96.94%]
Epoch 6/20: 100%|██████████| 94/94 [00:03<00:00, 27.78it/s, loss=0.0797, acc=97.56%, val_loss=0.0037, val_acc=97.18%]
Epoch 7/20: 100%|██████████| 94/94 [00:03<00:00, 27.48it/s, loss=0.0693, acc=97.90%, val_loss=0.0034, val_acc=97.52%]
Epoch 8/20: 100%|██████████| 94/94 [00:03<00:00, 27.15it/s, loss=0.0620, acc=98.12%, val_loss=0.0030, val_acc=97.81%]
Epoch 9/20: 100%|██████████| 94/94 [00:03<00:00, 26.14it/s, loss=0.0559, acc=98.30%, val_loss=0.0028, val_acc=98.09%]
Epoch 10/20: 100%|██████████| 94/94 [00:03<00:00, 27.63it/s, loss=0.0510, acc=98.48%, val_loss=0.0026, val_acc=98.14%]
Epoch 11/20: 100%|██████████| 94/94 [00:03<00:00, 24.55it/s, loss=0.0466, acc=98.60%, val_loss=0.0025, val_acc=98.23%]
Epoch 12/20: 100%|██████████| 94/94 [00:03<00:00, 26.40it/s, loss=0.0431, acc=98.70%, val_loss=0.0025, val_acc=98.25%]
Epoch 13/20: 100%|██████████| 94/94 [00:03<00:00, 26.93it/s, loss=0.0396, acc=98.79%, val_loss=0.0024, val_acc=98.33%]
Epoch 14/20: 100%|██████████| 94/94 [00:03<00:00, 26.35it/s, loss=0.0376, acc=98.84%, val_loss=0.0024, val_acc=98.36%]
Epoch 15/20: 100%|██████████| 94/94 [00:03<00:00, 27.65it/s, loss=0.0354, acc=98.91%, val_loss=0.0024, val_acc=98.39%]
Epoch 16/20: 100%|██████████| 94/94 [00:03<00:00, 27.16it/s, loss=0.0332, acc=98.99%, val_loss=0.0024, val_acc=98.41%]
Epoch 17/20: 100%|██████████| 94/94 [00:03<00:00, 25.94it/s, loss=0.0305, acc=99.08%, val_loss=0.0025, val_acc=98.36%]
Epoch 18/20: 100%|██████████| 94/94 [00:03<00:00, 27.69it/s, loss=0.0281, acc=99.13%, val_loss=0.0025, val_acc=98.31%]
Epoch 19/20: 100%|██████████| 94/94 [00:03<00:00, 28.22it/s, loss=0.0256, acc=99.21%, val_loss=0.0025, val_acc=98.31%]
Epoch 20/20: 100%|██████████| 94/94 [00:03<00:00, 28.84it/s, loss=0.0234, acc=99.31%, val_loss=0.0024, val_acc=98.32%]
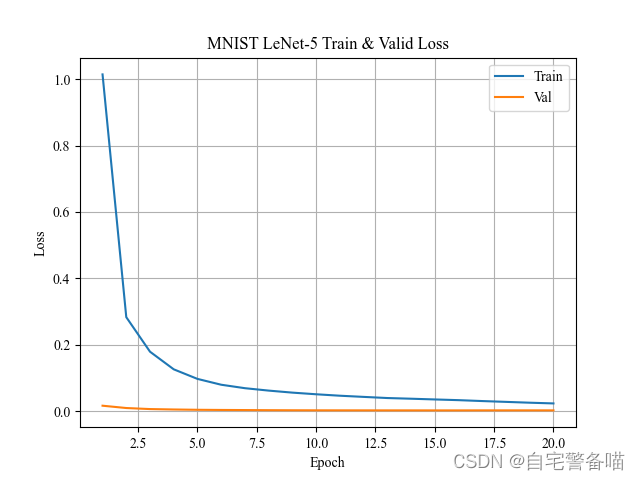
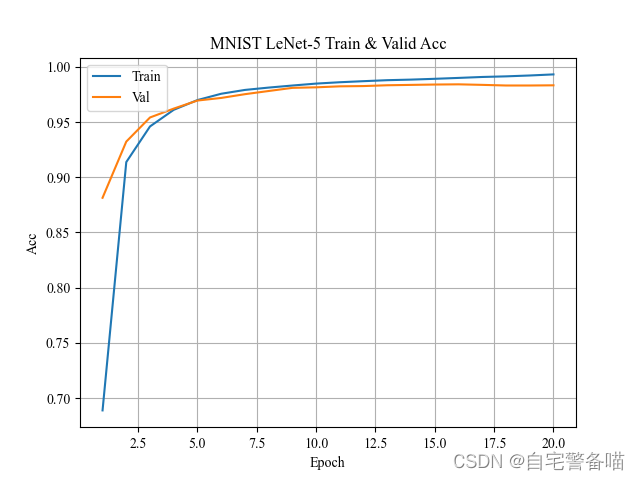
训练结果可视化
每次训练结束后,对训练过程的损失、准确率进行一定可视化,将更直观分析训练过程模型是否收敛。可视化模块采用matplotlib.pyplot,绘制图片如下:
def plot_train_history(history, num_epoch=epochs):
"""
对训练结果的可视化
Args:
history (dict): 训练结果字典(包含 loss 和 accuracy 键)
num_epoch (int): 展示周期数量(默认为 epochs)
Returns:
"""
keys = ['loss', 'acc']
for k in keys:
plt.plot(range(1, num_epoch + 1), np.mean(history[k]["train"][:num_epoch + 1], -1))
plt.plot(range(1, num_epoch + 1), np.mean(history[k]["val"][:num_epoch + 1], -1))
plt.legend(labels=['Train', 'Val'])
plt.title(f'MNIST LeNet-5 Train & Valid {k.title()}')
plt.xlabel('Epoch')
plt.ylabel(k.title())
plt.grid(True)
plt.show()
plot_train_history(train_history, epochs)








![[Java基础]基本概念(上)(标识符,关键字,基本数据类型)](https://img-blog.csdnimg.cn/bea8808e05e64be3b4b30446c351948c.png)