refs

• 参考经典机器学习资料西瓜书

主要符号

• $x$:标量

• $\mathbf{x}$:向量(注意是$x$的粗体形式)

• $\mathbf{x}$:变量集(正粗体)

• $\mathbf{A}$:矩阵(正粗体)

• $\mathbf{I}$:单位阵(正粗体)

• $\chi$:样本空间或状态空间

• $\mathcal{D}$:概率分布(字母D的书法体(caligraph))

• $D$:数据集(数据样本)

• $\mathcal{H}$:假设空间(Hypothesis,字母H的书法体)

• $H$:假设集

• $\mathfrak{L}$:学习算法(字母L的fraktur字体(哥特体),a German style of black-letter type.)

• $(\cdot ,\cdot ,\cdot )$:行向量

• $(\cdot ;\cdot ;\cdot )$列向量

• $(\cdot {)}^{\mathrm{T}}$向量(矩阵)转置(有时为了简单,将${}^{\mathrm{T}}$简记为${}^T$)

• { ⋯   } \{\cdots\} {⋯}:集合

• ∣ { ⋯   } ∣ |\{\cdots\}| ∣{⋯}∣:集合中元素个数

• $||\cdot |{|}_p$:${\mathrm{L}}_p$范数,$p$缺省时表示${\mathrm{L}}_2$范数(有时$\mathrm{L}$作$L$)

• $P(\cdot )$概率质量函数

• $P(\cdot |\cdot )$:条件概率质量函数

• $p(\cdot )$:概率密度函数

• $p(\cdot |\cdot )$:条件概率密度函数

• $\mathbb{E}.\sim \mathcal{D}[f(\cdot )]$:数学期望

  • 字母$E$的黑板粗体(blackboard)
  • 具体是函数$f(\cdot )$对$\cdot$在分布$\mathcal{D}$下的数学期望
  • 意义明确时省略$\mathcal{D}$和$\cdot$中的一个或全部

• $\sup (\cdot )$:上确界

• $\mathbb{I}(\cdot )$:指示函数,在$\cdot$为真时取1,否则取0($\mathbb{I}$是字母$I$的黑板粗体)

• $\text{sign}(\cdot )$:符号函数:

  • $$\text{sign}(\cdot )=\{\begin{array}{ll}-1,& \cdot <0\\ 0,& \cdot =0\\ 1,& \cdot >0\end{array}$$

基本概念

• 学习算法：从数据中产生模型的算法称为学习算法

• 机器学习是研究学习算法的学问

• 从数据中学得到的结果可称为模型

• 进行机器学习先要有数据：

  • 记录的集合称为数据集，记录是关于一个事件或对象的描述，也称为示例（instance)或样本(sample)
  • 属性(attribute)或特征(feature):反映事件或对象在某方面的表现或性质的事项
  • 属性值(attribute value):属性的取值

• 属性张成的空间成为属性空间(sample space),样本空间(smaple space)或输入空间

• 若样本包含n个属性,则可以张成一个n维空间

  • n维空间中的每个(n维)点都对应一个n维坐标向量,因此也可以将一个示例成为一个特征向量(feature vector)

• 令 D = { x 1 , x 2 , ⋯   , x n } D=\{\boldsymbol{x_1},\boldsymbol{x_2},\cdots,\boldsymbol{x_n}\} D={x1​,x2​,⋯,xn​}表示包含m个示例的数据集

• 若每个示例有$d$个属性描述(整数d称为样本${\mathbf{x}}_i$的维数(dimesionality),则可以表示为${\mathbf{x}}_i=(x_{i1},\cdots ,x_{id})$

  • $x_{ij}$表示${\mathbf{x}}_i$向量在第j个属性上的取值
  • ${\mathbf{x}}_i$是d维样本空间$\chi$中的一个向量,记为${\mathbf{x}}_i\in \chi$

• 学习(learning)或训练(training):从数据中学得模型的过程

  • 学习通过执行某个学习算法lai完成

• 训练过程中使用的数据称为训练数据(training data),每个样本称为具体称为训练样本(trianing sample)

• 训练集(traing set):寻来你样本组成的集合

• 假设(hypothesis):学习算法学得的模型对应的数据的某种潜在规律

• 真相(ground-truth):潜在规律自身(真实规律)

  • 学习过程是一个找出或逼近真相的过程

• 学习器(learner):模型的别称,可以看作学习算法在给定数据和参数空间上的实例化

• 标记(label):示例的标签(作为训练样本的结果信息)

  • 例如通过判断西瓜样本(色泽=青绿,根蒂=蜷缩,敲声=浑浊)->好瓜其中好瓜这个结论作为示例的标签

• 样例(example):拥有了标记的的示例(区别于样本sample)

• 预测(prediction):根据模型判断或估计新输入示例具有什么样的标签

• 记$({\mathbf{x}}_i,y_i)$表示第i个样例,$y_i\in \gamma$是${\mathbf{x}}_{\mathbf{i}}$的标记,$\gamma$是所有标记的集合,也称为标记空间(label space)或输出空间

• 对离散值的预测任务称为分类(classification)

  • 只需要区分2个类别得任务称为二分类(binary classification)
    • 其中一个类称为正类(positive class)
    • 另一个类称为负类(或反类)(negative class)
  • 类别超过2的情况,称为多分类(multi-class classification)

• 对非离散的连续值得预测任务是回归(regression)

• 预测任务:通过对训练集D进行学习,建立一个从$\chi$到$\gamma$的映射$f:\chi \to \gamma$

  • 对于二分类任务,$|\gamma |=2$,通常令 γ = { − 1 , + 1 } 或 { 0 , 1 } \gamma=\{-1,+1\}或\{0,1\} γ={−1,+1}或{0,1}
  • n分类任务$|\gamma |=n>2$
  • 对于回归任务,通常$\gamma =\mathbb{R}$,$\mathbb{R}$为实数集

• 训练好模型后,需要对模型进行测试(testing),被预测的样本称为测试样本(testing samle)

• 聚类:将训练集中样本分成若干组,每个组又称为簇(cluster)

  • 自动形成的簇可能对应了一些潜在概念的划分,例如西瓜的颜色,大小等可能不是我们要预测的目标(标签)

• 根据训练数据是否拥有标记信息,学习任务可大致划分为两大类:

  • “监督学习”(supervised learning)
    • 例如分类和回归任务
  • “无监督学习”(unsupervised learning)，
    • 例如聚类任务

• 需注意的是,机器学习的目标是使学得的模型能很好地适用于“新样本”，而不是仅仅在训练样本上工作得很好,即便对聚类这样的无监督学习任务,我们也希望学得的簇划分能适用于没在训练集中出现的样本.

  • 学得模型适用于新样本的能力,称为“泛化”(generalization)能力.
  • 具有强泛化能力的模型能很好地适用于整个样本空间.
    • 现实任务中样本空间的规模通常很大(例如20个属性,每个属性有10个可能取值，则样本空间的规模已达$10^{20}$)
  • 于是,尽管训练集通常只是样本空间的一个很小的采样，我们仍希望它能很好地反映出样本空间的特性，否则就很难期望在训练集上学得的模型能在整个样本空间上都工作得很好.

• 通常假设样本空间中全体样本服从一个未知“分布”(distribution)$\mathcal{D}$,我们获得的每个样本都是独立地从这个分布上采样获得的，即“独立同分布”(independent and identicallydistributed,简称i.i.d.)

• 一般而言,训练样本越多,我们得到的关于D的信息越多,这样就越有可能通过学习获得强泛化能力的模型.

假设空间

• 归纳(induction)与演绎(deduction)是科学推理的两大基本手段.
  • 归纳是从特殊到一般的“泛化”(generalization)过程,即从具体的事实归结出一般性规律;
  • 后者则是从一般到特殊的“特化”(specialization)过程,即从基础原理推演出具体状况．
• 例如
  • 在数学公理系统中,基于一组公理和推理规则推导出与之相洽的定理,这是演绎;
  • 而“从样例中学习”显然是一个归纳的过程,因此亦称“归纳学习”(inductive learning).

概念学习

• 归纳学习有狭义与广义之分
  • 广义的归纳学习大体相当于从样例中学习,
  • 狭义的归纳学习则要求从训练数据中学得概念(concept),因此亦称为“概念学习”或“概念形成”．
• 概念学习技术目前研究、应用都比较少,因为要学得泛化性能好且语义明确的概念太困难
• 现实常用的技术大多是产生“黑箱”模型.
• 对概念学习有所了解,有助于理解机器学习的一些基础思想.

经验误差和过拟合

常见概念🎈

• 错误率(error rate):分类错误的样本数占样本总数的比例
  • $E=\frac{a}{m}$其中m为样本总数,a为被分类错误的样本数
• 精度(accuracy):$A=1-E=1-\frac{a}{m}$,即精度=1-错误率
• 误差(error):学习器的实际预测输出与样本的真实输出之间的差异
  • 训练误差(training error|empirical error):也称经验误差,是学习器在训练集上的误差
  • 泛化误差(generalization error):学习器在新样本上的误差
• 我们总是希望得到泛化误差最小的学习器
  • 我们希望学习器从训练样本中能尽可能学出适用于所有潜在样本的普遍规律
• 此外,经验误差很小的学习器往往不是我们想要的,他们在多数情况下不好(过拟合)

泛化性能

过拟合

• 学习器把训练样本学得太好(过度),很可能把训练样本自身的一些特点当作潜在样本都有的一般性质,这现象显然是不好的行为,会影响泛化能力,称为过拟合(overfitting)
  • 常见的情况是学习器学习能力过于强大,导致把训练样本的特有特性都学习到了
  • 这是机器学习面临的关键问题
  • 过拟合无法彻底避免,我们只能缓解或减小过拟合风险

欠拟合

• 相反,如果对训练样本的一般性质尚未学好,则成为欠拟合(underfitting)
  • 通常由于学习能力低下造成,这类情况比较好克服,例如:
    • 对于决策树,可以扩展分支
    • 对于神经网络,可以增加训练轮数

例

• 例如:
  • 训练集中的树叶基本都有锯齿边,现在新的样本树叶没有锯齿,由于学习器把锯齿边作为样本是树叶的特征作了学习,因此无锯齿的新树叶样本被判定为不是树叶,这种现象理解为过拟合
  • 如果将一整棵树判定为一片树叶,则是欠拟合

模型选择问题

• 在解决进行某个任务的时候,可能有多种算法可供选择,对于同一中算法,使用不同的参数配置,也会产生不同的模型.
• 对算法的选择和参数配置的选择问题是机器学习中的模型选择(model selection)问题

评估方法(实验估计方案)

样本采样

• 划分测试集(训练集)要尽可能保持数据分布一致性,避免因数据划分过程中引入额外的偏差而对最终结果产生影响
• 分层采样(stratified sampling):在分类任务中,要保持样本的类别比例相似,以采样(sampling)的角度来看,保留类别比例的采样方式称为分层采样
  • 例如,训练集S中正例和反例都是$a:b$

测试集

• 测试集(testing set):测试学习器对新样本的判别能力,以测试集上的测试误差(testing error)作为泛化误差的近似

• 对于测试集,通常假设测试样本也是从样本真实分布中独立同分布采样而得.

• 假设我们有一个包含$m$个样例的数据集$D=\{({\mathbf{x}}_1,y_1),({\mathbf{x}}_2,y_2),\cdots ,({\mathbf{x}}_m,y_m)\}$,可以通过各种方法从D中产生处训练集$S$和测试集$T$

留出法

• 留出法(hold-out),将D划分为两个互斥的集合,其中一个作为训练集S,另一个作为测试集T
  • $D=S\cup T$,$S\cap T=\varnothing$
  • 在S上训练出模型后,用T对模型进行评估(评估器测试误差,作为对泛化误差的估计)
• 单次使用留出法得到的估计结果往往是不够稳定可靠,使用留出法一般要要采用若干次随机划分,重复进行试验评估后取平均值作为留出法的评估结果

保真性

• 通常希望评估数据集D上训练的模型,留出法需要分割训练集和测试集
  • 如果训练集S样本数量接近D,则模型可能更加接近直接用D训练出来的模型,但T此时较小,评估结果可能不够稳定准确
  • 反之,较大的T使得S和D差距变大,基于S训练出来的模型和D训练的模型可能有较大差别,降低了评估结果的保真性(fidelity)
• 通常做法是将$\frac{2}{3}\sim \frac{4}{5}$的样本作为训练集,剩余样本作为测试

交叉验证法

• 交叉验证法(cross validation):先将数据集D划分为k个大小相似的互斥子集
  • $D=D_1\cup D_2\cup \cdots \cup D_k={\bigcup }_{i=1}^k{D}_i$
  • $D_i\cap D_j=\varnothing ,i\ne j$
  • 每个子集$D_i$都尽可能保持数据分布的一致性(从D中通过分层采样得到(stratified k-fold))
  • 这类划分可供k次试验(训练+测试),每次用k-1个子集的并集作为训练集,剩余的一个子集作为测试集
  • 最终对k次试验的测试结果取平均值返回
• 交叉验证法的稳定性和保真性很大程度取决于k的取值,通常把交叉验证法称为k折交叉验证($k-fold$ cross validation)
• k通常取10,5,20等

p次k折交叉验证

• 将数据集D划分为k个子集存在多种划分方式
• 为例减少因样本划分的不同而引入的差异,k折交叉验证通常要随机使用不同的划分重复p次
• 最终的评估结果是p次k折交叉验证结果的均值(总共执行$p\times k$次试验(训练+测试),相当执行了$p\times k$次留出法试验)

留一法

• 假设数据集D中包含m个样本,若令$k=m$,则得到交叉验证法的一个特例:留一法(Leave-One-Out,LOO).
• LOO不受随机样本划分方式的影响,因为m个样本只有唯一的方式:划分为m个子集,且每个子集包含一个样本
• LOO的S集和D集样本数量只差1,因此绝大多数情况下,LOO中被实际评估的模型(基于S)和期望评估的模型(基于D)和相似.
• LOO的评估结果往往被认为比较准确.
• 容易发现,LOO在需要做$1\times m$次试验,即,需要训练m个模型,评估测试结果求平均值
• 在数据集很大时,m很大,训练你m个模型的计算开销可能非常大,如果再算上调参,则更加让人难以接受.

自助法

• 在留出法和交叉验证法中,由于保留了D中的一部分T作为测试集,因此实际评估的模型所用的训练集S比D小,引入了一些因为训练样本规模不同而导致的估计偏差.
• 虽然留一法受训练样本规模变化影响较小,但是计算代价太高
• 自助法(bootstrapping)是一个较好的解决方案,可以减少样本训练样本规模不同造成的影响,同时还能比较高县地进行实验估计,它直接以自助采样法为基础:

自主采样法

• 自助采样法(bootstrap sampling),设数据集D包含m个样本,对齐进行采样得到数据集$D^{\prime }$:

  • 每次从D中挑选一个样本,将其拷贝到D’,被拷贝的样本放回D中
  • 将上述过程重复m次,得到包含m个样本的数据集$D^{\prime }$,作为自助采样的结果
  • D中的一部分会出现在D’中,另一部分不出现

• 任何样本每次采样中被采到的概率总是$\frac{1}{m}$,不被采到的概率为$1-\frac{1}{m}$

• 某个样本m次采样始终不被采到的概率:$(1-\frac{1}{m}{)}^m$,对其取极限:

  • $$\underset{m\to \infty }{\lim }(1-\frac{1}{m}{)}^m=e^{-1}\approx 0.368$$

  • 注意m既是是样本总数,同时也是采样次数

• 通过自助采样(m足够大),初始数据集D中约有36%的样本未出现在采样数据集$D^{\prime }$中

• 我们可以采用$D^{\prime }$作为训练集,$S=D\backslash D^{\prime }$作为测试集

  • $D\backslash D^{\prime }$中,\(backslash)集合减法,相当于$D-D^{\prime }$
  • 这样,实际评估的模型与期望评估的模型都是用m个训练样本,而且,根据上面的极限值$1/e$,仍然有$\frac{1}{3}$左右的样本不会被用于训练(不再训练集$D^{\prime }$中出现)
  • 上述方法称为包外估计(out-of-bag estimate)

• 优点:

  • 自助法在数据集较小,那一有效划分训练/测试集时很有用
  • 自助法能够从初始数据集中产生多个不同的训练集,对集成学习很有用

• 缺点:

  • 自助法产生的数据集改变了初始数据集的分布,引入了估计偏差(因此,当数据量充足时,更多的使用留出法和交叉验证法)

调参

• 参数调剂或调参(parameter tuning),大多数机器学习算法有些参数(parameter)需要设定,参数配置不同,学习器学习得得模型性能可能有显著差别
• 学习算法很多参数时在实数范围内取值,显示做法时对每个参数选定一个范围和变化步长
  • 例如,[m,m+0.2]内以0.05为步长,那么需要参加评估的候选参数有$0.2/0.05+1=5$个
  • 这种离散的选择参数结果往往不是最佳的,但为例学习过程变得可行,需要对计算开县和性能估计之间机型着折衷,采用一系列的离散值作为候选参数
  • 此外,即便是折中后的做法,对于有多个参数需要调节的算法,依然可能要做大量的模型考察,假设算法有a个参数需要调整,每个参数仅考虑b个候选值,则就产生了$b^a$中不同的参数组合

模型交付

• 上述介绍的训练/评估方法都对数据集D做了一定的预留(作为测试集)进行评估和测试,因此事实上只用了一部分数据训练模型
• 当模型选择工作完成后,学习算法和参数配置已经选定.这时要用数据集D重新对选定后的算法和配套参数配置进行训练(这个模型在训练过程中使用了所有m个样本),作为最终模型

测试数据和验证数据

• 为了区分,通常把模型在实际使用过程中遇到的数据称为测试数据,对应于测试集

• 模型评估和选择阶段用于评估测试的数据集称为验证集(validation set)

• 对比不同算法的泛化性能时,从数据集划分一部分作为测试集,用测试集上的判别效果来估计模型在实际使用时的泛化能力

• 把训练数据另外划分为训练集和测试集,基于验证集上的性能来进行模型选择和调参

• 例如,数据集D本划分为测试集T和S=D-T,使用一下实验基于S

  • 对算法A选中参数配置P1,使用交叉验证法评估训练出来的模型性能,得到评估结果R1
  • 假设该模型性能不能令人满意,我们再选择一组参数P2,再次训练,重新评估,得到评估结果R2
  • 反复执行上述过程,直到得到满意的评估结果位置,记录此时的参数配置
  • 这个过程中S被划分为SS和SV,分别作为单次实验中的训练集和验证集
  • 可见,验证集其实是训练数据中的一部分

性能度量

• 对学习器的泛化性能进行评估，不仅需要有效可行的实验估计方法，还需要有衡量模型泛化能力的评价标准，这就是性能度量(performance measure).
• 性能度量反映了任务需求,对比不同模型的能力时,可能选用不同的性能度量,而不同的性能度量可能产生不同的评判结果(意味着模型的好坏时相对的,比如A模型再M1度量指标上好于B模型,但B模型可能再M2度量指标上好于模型A)
• 模型的好坏不仅仅取决于算法和数据,还取决于任务需求
• 设样例集$D=\{({\mathbf{x}}_1,y_1),\cdots ,({\mathbf{x}}_m,y_m)\}$其中$y_i$是样本${\mathbf{x}}_i$的真实标记
• 通过比较学习器的预测结果$f(\mathbf{x})$和真实标记$y$来评估学习器$f$的性能

均方误差

• 回归任务最常用的性能度量是均方误差(mean squared error),MSE:

  • $$E(f;D)=\frac{1}{m}\sum _{i=1}^m(f({\mathbf{x}}_{\mathbf{i}})-y_i{)}^2$$

• 对于数据分布D和概率密度函数p,MSE描述为:

  • $$E(f;D)={\int }_{x\sim D}(f(\mathbf{x})-y{)}^{2}p(\mathbf{x})\mathrm{d}\mathbf{x}$$

指示函数符号

• $\mathbb{I}$符号表示指示函数($\mathbb{I}(\cdot )$表示表达式$\cdot$为真时,结果取1,否则取0)

错误率

• $$\begin{gathered} E(f;D)=\frac{1}{m}\sum _{i=1}^m\mathbb{I}(f({\mathbf{x}}_{\mathbf{i}})\ne y_i) \\ 对于数据分布D和概率密度函数p \\ E(f;D)={\int }_{x\sim D}\mathbb{I}(f(\mathbf{x})\ne y)p(\mathbf{x})\mathrm{d}\mathbf{x} \end{gathered}$$

精度

• $$\begin{gathered} acc(f;D)=1-E(f;D) \\ 具体分为离散情况:\frac{1}{m}\sum _{i=1}^m\mathbb{I}(f({\mathbf{x}}_{\mathbf{i}})=y_i) \\ 非离散情况:{\int }_{x\sim D}\mathbb{I}(f(\mathbf{x})=y)p(\mathbf{x})\mathrm{d}\mathbf{x} \end{gathered}$$

混淆矩阵

• 二分类中,真实类别$y$和学习器预测类别$f(\mathbf{x})$的组合划分为:

  • True Positive,TP,真正例,真阳例
  • False Positive,FP,假正例,假阳例
  • True Negative,TN,真反例,真阴例
  • False Negative,FN,假反例,假阴例

• 假设样本总数为m,满足:

  • TP+FP+TN+FN=m

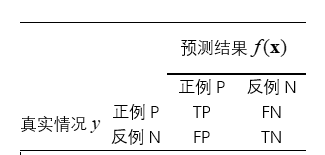
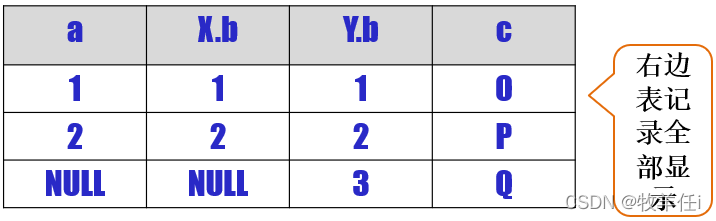
  • 混淆矩阵	黄色部分表示预测为正例的样本
    这是二分类情况下的,多分类有类似的推广概念	蓝字部分表示真实为正例的样本

precision

• precision,有多种译法:查准率,准确率

• $$P=\frac{TP}{TP+FP}$$

• 区别于上面提到的精度,错误率和精度是更加综合的指标,而precision和recall是更加具体的指标

recall

• recall,有多种译法:查全率,回召率

• $$R=\frac{TP}{TP+FN}$$

precision和recall的矛盾

• 通常,P,R是一对矛盾的度量
  • P高R往往偏低
  • R高P往往偏低
• 以选西瓜为例,假设瓜的总量丰富
• 如果十分保守,只选非常有把握的瓜(挑出的瓜中好瓜比例尽量高),那么可以提高P
  • 因为FP会减小,从而FN变大,导致R变小
  • 会导致许多好瓜被遗漏
  • 对于内容推荐这类任务,通常希望查准率高,推荐给用户的内容尽可能使用户喜欢的,没有较高把握用户喜欢的内容就不推荐了,这些遗漏通常不太重要.
• 尽可能多的选瓜,可以提高R(查全率)
  • 因为TP变大,FP增大,FN不会变大,反而会减少,导致P变小
  • 但是导致差的瓜被选中(成为假阳例),导
  • 例如传染病病毒检测中,希望减少遗漏阳性患者的可能,更加关心查准率
  • 逃犯的搜查也是类似的
• 只有在一些简单的任务中,P,R才会同时比较高

P-R曲线图

• sklearn.metrics.precision_recall_curve — scikit-learn documentation
• P-R 图直观地显示出学习器在样本总体上的查全率、查准率.
• 
• 在进行比较时，若一个学习器的P - R 曲线被另一个学习器的曲线完全“包住”，则可断言后者的性能优于前者
• 例如曲线A完全包住曲线C,称A地性能由于C
• 如果P-R曲线发生交叉,则不容易比较好坏

BEP平衡点

• BEP(Break Event Point)使P-R曲线上P=R时的位置,距离原点越远,则认为BEP越好,可以作为简单的综合指标,来比较P-R曲线发生交叉时的粗略比较

$F_1,F_{\beta }$

• 由于BEP过于简单,更常用的是F1度量(P,R的调和平均数):

  • $$F1=\frac{2PR}{P+R}$$

• $F_1$是基于P,R的调和平均(harmonic mean)定义的

  • 调和平均数比算数平均数和集合平均数更加重视较小值

  • $$F_1^{-1}=\frac{1}{2}(P^{-1}+R^{-1})$$

• $F_{\beta }$

  • 某些任务更加看重P,R中的一方

  • 则考虑使用$F_1$的一般形式:$F_{\beta }$,借助$\beta$表达我们对P,R的不同偏好程度

  • $$F_{\beta }=\frac{(1+{\beta }^2)PR}{({\beta }^{2}P)+R}$$

  • 可以看到$F_1$是$\beta =1$时的特例

  • $\beta >0$度量了R对P的相对重要性

    • $\beta >1$时R有更大的影响
    • $\beta <1$时则相反(P有更大影响)

macro@micro

• 对于多个二分类混淆矩阵$C_1,\cdots ,C_n$，例如
  • 进行多次训练+测试，每次可得到一个混淆矩阵
  • 在多个数据集上进行训练+测试，每个数据集上的实验都可以得到混淆矩阵，以估计算法的全局性能
• 多分类任务中，每两两个类别的组合都对应一个混淆矩阵，也可以获得多个混淆矩阵

macro

• 宏查准率(macro-P)和宏查全率(macro-R)：
  • 在各个混淆矩阵上分别计算出P和R,记为$(P_1,R_1),(P_2,R_2),\cdots ,(P_n,R_n)$,再计算平均值,得到macro-P,macro-R
  • macro-P=$\frac{1}{n}{\sum }_{i=1}^n{P}_i$,简记为$P_M$
  • macro-R=$\frac{1}{n}{\sum }_{i=1}^n{R}_i$,简记为$R_M$
• 宏F1(macro-F1):
  • macro-F1=$\frac{2P_M{R}_M}{P_M+R_M}$,简记为$F_{1M}$

micro

• 若将各混淆矩阵的对应元素(即TP,FP,TN,FN)各自进行平均,得到的平均值分别记为$\overline{TP},\overline{FP},\overline{TN},\overline{FN}$

• micro-P,简记为$P_m$

  • $$P_m=\frac{\overline{TP}}{\overline{TP}+\overline{FP}}$$

• micro-R,简记为$R_m$

  • $$R_m=\frac{\overline{TP}}{\overline{TP}+\overline{FN}}$$

• micro-F1,简记为$F_{1m}$

  • $$F_{1m}=\frac{2P_m{R}_m}{P_m+R_m}$$

ROC

• 很多学习器是为测试样本产生一个实值或概率预测(统称为预测值),然后将这个预测值与一个分类阈值(threshold)进行比较,若大于阈值则分为正类,否则为反类．
• 例如,神经网络在一般情形下是对每个测试样本预测出一个[0.0,1.0]之间的实值,然后将这个值与0.5进行比较,大于0.5则判为正例,否则为反例.
• 这个实值或概率预测结果的好坏,直接决定了学习器的泛化能力.

截断点

• Multiclass Receiver Operating Characteristic (ROC) — scikit-learn documentation

• 实际上,根据这个实值或概率预测结果，我们可(根据各样本的预测值)将测试样本进行排序，“最可能”是正例的排在最前面,“最不可能”是正例的排在最后面.这样,分类过程就相当于在这个排序中选用某个“截断点”(cut point)将样本分为两部分,前一部分判作正例,后一部分则判作反例.

• 在不同的应用任务中,我们可根据任务需求来采用不同的截断点，例如若我们更重视“查准率”，则可选择排序中靠前的位置进行截断(尽可能选择比较有把握的样本);若更重视“查全率”,则可选择靠后的位置进行截断.

• 因此,排序本身的质量好坏,体现了综合考虑学习器在不同任务下的“期望泛化性能”的好坏,或者说，“一般情况下”泛化性能的好坏.

• ROC曲线则是从这个角度出发来研究学习器泛化性能的有力工具.

  • ROC全称是“受试者工作特征”(Receiver Operating Characteristic)曲线，它源于“二战”中用于敌机检测的雷达信号分析技术，二十世纪六七十年代开始被用于一些心理学、医学检测应用中,此后被引入机器学习领域

  • 与P-R曲线相似,我们根据学习器的预测结果对样例进行排序,按此顺序逐个把样本作为正例进行预测,每次计算出两个重要量的值,分别以它们为横、纵坐标作图,就得到了“ROC曲线”.

  • 与P-R曲线使用查准率、查全率为纵、横轴不同, ROC曲线的纵轴是“真正例率”(True Positive Rate,简称TPR),横轴是“假正例率”(False PositiveRate,简称FPR)

  • $$\begin{gathered} TPR=\frac{TP}{TP+FN} \\ FPR=\frac{FP}{TN+FP} \end{gathered}$$

  • 更具表达式比较可以发现TPR就是回召率(查全率)R

• ROC曲线图简称ROC图

  • 对角线对应于随机猜测模型,因为所有反例样本被预测错的比例和所有正例样本被正确预测的比例相同,对于二分类任务,效果相当于随机猜测
  • 对于点$(0,1)$表示模型能够将所有正例样本预测为正例,所有反例样本预测为反例(也就是所有样例都被正确预测),属于最理想的情况.从cut point的角度来看,就是截断点之前的样本都是正例,截断点之后的样例都是反例

• 现实任务中,无论是P-R图还是ROC图,都仅能获得有限个坐标对,而无法获得真正光滑的ROC曲线,只能绘制出近似的ROC曲线

  • 

• ROC曲线的绘制(描点方法):

  • 给定$m_{+}$各正例和$m_{-}$个反例($m_{[-]}+m_{[+]}=n$,对学习器预测结果对样例进行排序
    • 不妨将n个样本的预测结果排序后的有序序列记为$[s_1,\cdots ,s_n]$,其中$s_i⩾s_j(0<i<j⩽0)$
  • 先把分类阈值(threshold)设置为最大($s_1$),这相当于将所有样例预测为反例,此时TPR,FPR均为0(TP,FP都为0),在坐标$(0,0)$出标记第一个点
  • 将threshold依次设置为$s_i(i=2,\cdots ,n)$,则个过程相当于依次将每个样本划分为正例部.
    • 设前一个标记点坐标为(x,y),对应的(TP,FP)=(a,b),则$(x,y)=(\frac{a}{m_{-}},\frac{b}{m_{+}})$
      • 若当前样例为TP,则对应的标记点为$(\frac{a}{m_{-}},\frac{b+1}{m_{+}})=(x,y+\frac{1}{m_{+}})$
      • 若当前例为FP,则对应的标记点为$(\frac{a+1}{m_{-}},\frac{b}{m_{+}})=(x+\frac{1}{m_{-}},y)$
  • 将生成的n个点依次连接得到近似ROC曲线

AUC

• 进行学习器比较时,与P-R图类似,如果学习器A的ROC曲线被学习器B的曲线完全包住,则认为B由于A

• A,B的ROC曲线发生交叉,则难以直接比较优劣,一个比较合理的判据时ROC曲线下的面积,AUC(Aera Under ROC Curve)

• 假定ROC是由坐标序列$\{(x_1,y_1),(x_2,y_2),\cdots ,(x_m,y_m)\}$的点按序列连接而形成(其中,$x_1=0,x_m=1$)

• $$AUC\approx \frac{1}{2}\sum _{i=1}^{m-1}(x_{i+1}-x_i)(y_i+y_{i+1})$$

• 给定$m_{+}$个正例和$m_{-}$个反例,令$D^{+},D^{-}$分别表示正,反例集合,排序损失(loss)定义为:

  • $$L_{rank}=\frac{1}{m_{+}{m}_{-}}\sum _{x^{+}\in D^{+}}\sum _{x^{-}\in D^{-}}\left(\mathbb{I}(f(x^{+})<f(x^{-}))+\frac{1}{2}\mathbb{I}(f(x^{+}=f(x^{-})))\right)$$

  • 考虑每一对正,反例

    • 若正例的预测值小于反例,则记一个罚分
    • 若相等,则记0.5个罚分

  • $L_{rank}$对应的是ROC曲线之商的面积,$AUC=1-L_{rank}$

  • 若一个正例在ROC曲线上对应的坐标为$(x,y)$,则$x$恰是排序在其之前的反例所占的比例(FPR)

比较检验

• 有了实验评估方法和性能度量,看起来就能对学习器的性能进行评估比较了:
  • 先使用某种实验评估方法测得学习器的某个性能度量结果,然后对这些结果进行比较.
• 实际上比直接取得性能度量的值然后比大小要复杂得多,重要因素:
  • 首先,我们希望比较的是泛化性能,然而通过实验评估方法我们获得的是测试集上的性能,两者的对比结果可能未必相同;
  • 第二,测试集上的性能与测试集本身的选择有很大关系,不同大小的测试集会得到不同的结果,即便用相同大小的测试集,若包含的测试样例不同,测试结果也会有不同;
  • 第三,很多机器学习算法本身有一定的随机性,即便用相同的参数设置在同一个测试集上多次运行,其结果也会有不同.
• 统计假设检验(hypothesis test)为我们进行学习器性能比较提供了重要依据.
• 基于假设检验结果我们可推断出,若在测试集上观察到学习器A比B好,则A的泛化性能是否在统计意义上优于B,以及这个结论的把握有多大.

偏差和方差

• Bias–variance tradeoff - Wikipedia

• 在机器学习中，偏差（bias）和方差（variance）是用来描述模型的两个重要特性。

• 偏差是指模型的预测值与真实值之间的差异，即模型本身的准确性。如果一个模型的偏差很高，则说明模型对训练数据的拟合程度不够，可能存在欠拟合的问题。

• 方差是指模型在不同数据集上预测结果的差异，即模型的稳定性。如果一个模型的方差很高，则说明模型对训练数据过度拟合，对新数据的预测能力不足，可能存在过拟合的问题。

偏差-方差分解(TODO)

• 偏差方差分解(bias-variance decomposition)是解释学习算法泛化性能的重要工具,本文将其简称为BVD
• BVD尝试对学习算法期望泛化错误率进行拆解.
  • 算法在不同训练集,甚至同分布的不同训练集上学得的结果可能是不同的.
• 对测试样本$\mathbf{x}$
  • 令$y_D$为$\mathbf{x}$在数据集中的标记
  • y为$\mathbf{x}$为真实标记
  • $f(\mathbf{x};D)$为训练集D上学得模型$f$在$\mathbf{x}$上得预测输出
• 以回归任务为例.

折衷方案

In statistics and machine learning, the bias–variance tradeoff is the property of a model that the variance of the parameter estimated across samples can be reduced by increasing the bias in the estimated parameters. The bias–variance dilemma or bias–variance problem is the conflict in trying to simultaneously minimize these two sources of error that prevent supervised learning algorithms from generalizing beyond their training set:[1][2]

• The bias error is an error from erroneous assumptions in the learning algorithm. High bias can cause an algorithm to miss the relevant relations between features and target outputs (underfitting).
• The variance is an error from sensitivity to small fluctuations in the training set. High variance may result from an algorithm modeling the random noise in the training data (overfitting).

The bias–variance decomposition is a way of analyzing a learning algorithm’s expected generalization error with respect to a particular problem as a sum of three terms, the bias, variance, and a quantity called the irreducible error, resulting from noise in the problem itself.

• 在统计学和机器学习中，偏差-方差权衡（bias-variance tradeoff）指的是模型的参数在样本之间估计的方差可以通过增加估计参数的偏差来减少。

• 偏差-方差困境或偏差-方差问题是指在尝试同时最小化这两个误差源的情况下，阻止监督学习算法超越其训练集进行泛化的冲突。

• 偏差误差是由于学习算法中的错误假设而导致的误差。

  • 高偏差可能导致算法忽略特征和目标输出之间的相关性（欠拟合）。

• 方差误差是由于对训练集中的微小波动过于敏感而导致的误差。

  • 高方差可能是由于算法对训练数据中的随机噪声进行建模（过拟合）。

偏差-方差分解是一种分析学习算法在特定问题上的预期泛化误差的方法，将其表示为偏差、方差和一个称为不可避免误差的量的总和，该量由问题本身的噪声引起。

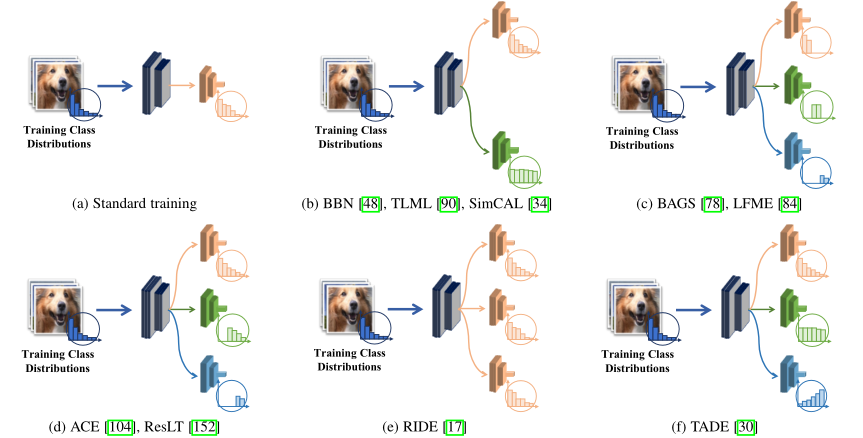
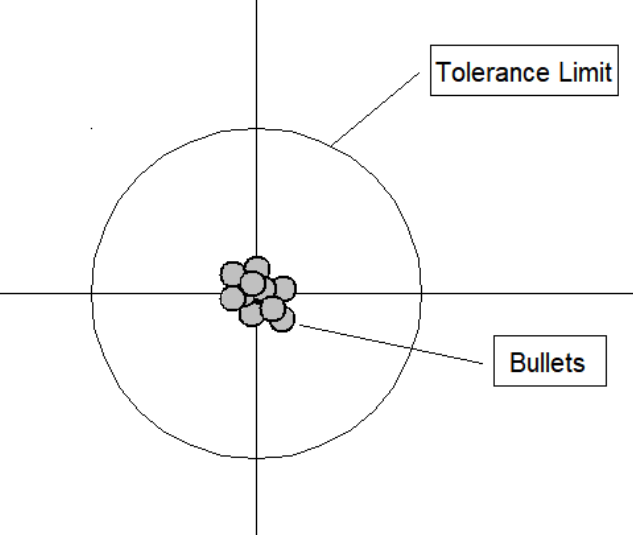	低偏差-低方差		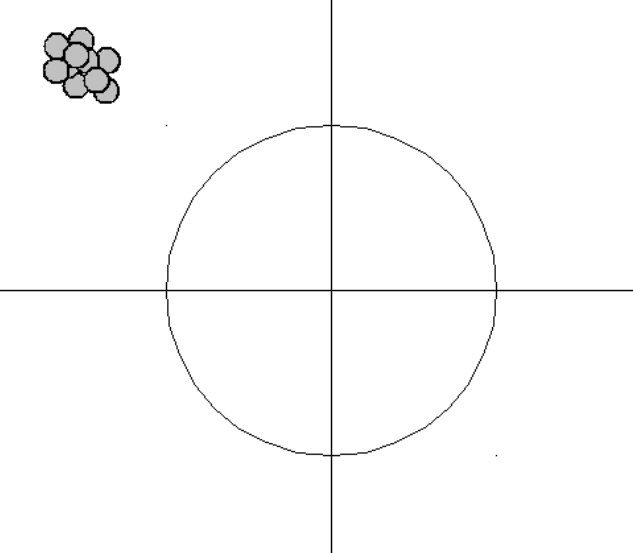高偏差-低方差
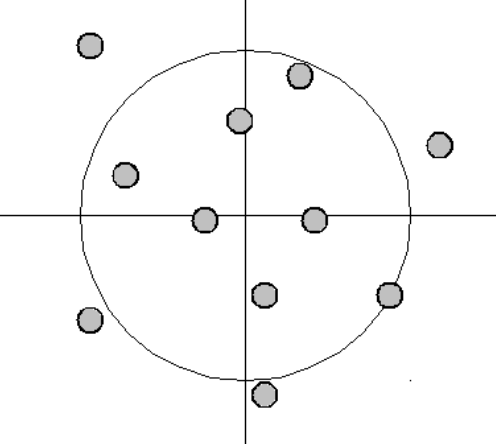	低偏差-高方差		高偏差-高方差

---

• The bias–variance tradeoff is a central problem in supervised learning. Ideally, one wants to choose a model that both accurately captures the regularities in its training data, but also generalizes well to unseen data. Unfortunately, it is typically impossible to do both simultaneously. High-variance learning methods may be able to represent their training set well but are at risk of overfitting to noisy or unrepresentative training data. In contrast, algorithms with high bias typically produce simpler models that may fail to capture important regularities (i.e. underfit) in the data.偏差-方差权衡是监督学习中的一个核心问题。理想情况下，我们希望选择一个既能够准确地捕捉训练数据中的规律，又能够很好地泛化到未见过的数据的模型。然而，通常情况下，两者无法同时实现。高方差的学习方法可能能够很好地表示它们的训练集，但存在过度拟合到噪声或不具代表性的训练数据的风险。相比之下，具有高偏差的算法通常会产生简单的模型，可能无法捕捉数据中的重要规律（即欠拟合）。

• It is an often made fallacy to assume that complex models must have high variance; High variance models are ‘complex’ in some sense, but the reverse needs not be true[clarification needed]. In addition, one has to be careful how to define complexity: In particular, the number of parameters used to describe the model is a poor measure of complexity. This is illustrated by an example adapted from: The model $f_{a,b}(x)=a\sin (bx)$ has only two parameters ($a,b$) but it can interpolate any number of points by oscillating with a high enough frequency, resulting in both a high bias and high variance.有一个常见的谬论是认为复杂的模型必须具有高方差；高方差的模型在某种意义上是“复杂”的，但反过来并不一定成立。此外，我们必须小心如何定义复杂性：特别是，用于描述模型的参数数量是一个不好的复杂度度量。这可以通过一个例子来说明：模型$f_{a,b}(x)=a\sin (bx)$只有两个参数($a,b$)，但是它可以通过高频振荡来插值任意数量的点，导致既有高偏差又有高方差。

• An analogy can be made to the relationship between accuracy and precision.

• Accuracy is a description of bias and can intuitively be improved by selecting from only local information. Consequently, a sample will appear accurate (i.e. have low bias) under the aforementioned selection conditions, but may result in underfitting. In other words, test data may not agree as closely with training data, which would indicate imprecision and therefore inflated variance.

• A graphical example would be a straight line fit to data exhibiting quadratic behavior overall.

• 可以将偏差-方差权衡和准确度和精度之间的关系进行类比。

• 准确度是偏差的描述，可以通过只选择局部信息来直观地提高。因此，在上述选择条件下，样本将看起来准确（即偏差小），但可能导致欠拟合。换句话说，测试数据可能与训练数据不太吻合，这将表明精度不高，因此方差膨胀。
  一个图形化的例子是将一条直线拟合到总体呈二次函数行为的数据上。

• Precision is a description of variance and generally can only be improved by selecting information from a comparatively larger space. The option to select many data points over a broad sample space is the ideal condition for any analysis. However, intrinsic constraints (whether physical, theoretical, computational, etc.) will always play a limiting role. The limiting case where only a finite number of data points are selected over a broad sample space may result in improved precision and lower variance overall, but may also result in an overreliance on the training data (overfitting). This means that test data would also not agree as closely with the training data, but in this case the reason is due to inaccuracy or high bias. To borrow from the previous example, the graphical representation would appear as a high-order polynomial fit to the same data exhibiting quadratic behavior. Note that error in each case is measured the same way, but the reason ascribed to the error is different depending on the balance between bias and variance. To mitigate how much information is used from neighboring observations, a model can be smoothed via explicit regularization, such as shrinkage.

• 为了取得好的预测结果，需要在偏差和方差之间进行折衷。

• 如果模型的偏差和方差都很高，则需要增加模型的复杂度，增加模型的参数或使用更复杂的算法；

  • 如果模型的偏差和方差都很高，说明模型很可能存在过拟合（overfitting）的问题。过拟合是指模型在训练数据上过度拟合，导致对新的数据的预测效果较差。
  • 模型的偏差很高意味着模型无法很好地拟合训练数据，而模型的方差很高则表明模型过度关注训练数据的噪声或随机性，从而对训练数据过度拟合。

小结

• 如果模型的偏差很高而方差很低，则需要减少模型的复杂度，减少模型的参数或使用更简单的算法；
  • 如果模型的偏差很高而方差很低，说明模型对训练数据的拟合程度不够，但是对新的数据具有较好的泛化能力。这种情况通常称为欠拟合（underfitting）。模型的偏差很高意味着模型的表现能力不足，无法很好地捕捉数据的特征，或者模型的参数设置不合理，模型本身的复杂度不够。而模型的方差很低则表明模型对数据的随机性不敏感，即不会因为数据的微小变化而导致预测结果产生较大的波动。
  • 解决欠拟合问题的方法包括增加模型的复杂度，如增加模型的参数或使用更复杂的算法，或者增加训练数据的数量。但是需要注意，过度增加模型的复杂度也可能导致过拟合问题，因此需要在模型的偏差和方差之间进行平衡，找到最优的模型复杂度。
• 如果模型的偏差很低而方差很高，则需要增加训练数据的数量或使用正则化等方法来减少过拟合的问题。