三个数学难题:

群的定义:

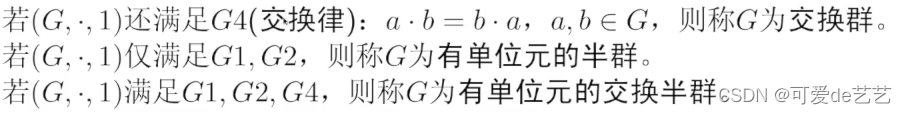
 满足乘法结合律，有单位元，逆元即为群，如果同时满足交换律则为交换群

满足乘法结合律，有单位元即为半群，如果同时满足交换律则为交换半群 

希尔密码:

 其中加密矩阵为n阶一般线性群，在本例中矩阵元素为0到25的数字

子群：

循环群并定义生成元的概念:

置换的定义:

 也就是一个集合S映射到自己，并且这个映射是双射，则为置换

对称群的概念:

 

置换密码:对应的是明文中字符位置映射

 第二行是明文的位置，第一行是密文的位置，这里是指把明文第四个位置换到第一个位置，以此类推，解密即为逆映射，把这两行调换即可

代换密码:对应的是字母表上的字母映射

 这里是第一行为明文，第二行为密文，逆映射同样是把两行调换

离散对数问题:

 模n乘:乘完模n，Zn表示0到n-1有n个元素的整数，Zn*表示有素数个元素的集合

  

 如果运算定义成了实数+，那么a^x=a+a+a...共x次，所以是b=xa