[入门必看]数据结构5.4：树、森林

news2024/11/23 11:47:47

[入门必看]数据结构5.4：树、森林

  • 第五章 树与二叉树
  • 5.4 树、森林
    • 知识总览
      • 5.4.1 树的存储结构
      • 5.4.2 树、森林与二叉树的转化
      • 5.4.3 树和森林的遍历
    • 5.4.1 树的存储结构
      • 树的逻辑结构
      • 回顾：二叉树的顺序存储
      • 如何实现树的顺序存储？
      • 树的存储1：双亲表示法
        • 拓展：双亲表示法存储“森林”
        • 双亲表示法的优缺点
      • 树的存储2：孩子表示法
        • 拓展：孩子表示法存储“森林”
        • 孩子表示法的优缺点
      • 树的存储3：孩子兄弟表示法
        • 拓展：孩子兄弟表示法存储“森林”
    • 5.4.2 树、森林与二叉树的转化
      • 树->二叉树的转换
      • 森林->二叉树的转换
      • 二叉树->树的转换
      • 二叉树->森林的转换
    • 5.4.3 树和森林的遍历
      • 树的逻辑结构
      • 树的先根遍历
      • 树的后根遍历
      • 树的层次遍历
      • 森林的先序遍历
      • 森林的中序遍历
  • 知识回顾与重要考点
    • 5.4.1 树的存储结构
    • 5.4.2 树、森林与二叉树的转化
    • 5.4.3 树和森林的遍历

第五章 树与二叉树

小题考频：30
大题考频：8

5.4 树、森林

难度：☆☆☆

知识总览

5.4.1 树的存储结构

在这里插入图片描述

5.4.2 树、森林与二叉树的转化

在这里插入图片描述

5.4.3 树和森林的遍历

在这里插入图片描述

5.4.1 树的存储结构

在这里插入图片描述

树的逻辑结构

在这里插入图片描述

树是一种递归定义的数据结构
一棵树要么是空树，要么至少有一个根结点，根结点的下方可能有零棵或多棵互不相交的子树。

二叉树：一个分支结点最多只能有两棵子树
树：一个分支结点可以有多棵子树

如何用顺序存储来存储树这种数据结构？

回顾：二叉树的顺序存储

在这里插入图片描述

二叉树的顺序存储：按照完全二叉树中的结点顺序，将各结点存储到数组的对应位置。数组下标反映结点之间的逻辑关系
在这里插入图片描述

顺序存储二叉树时，结点编号会和完全二叉树对应。
那么这种思路能否推广到普通的树？

如何实现树的顺序存储？

在这里插入图片描述

由于每个分支结点的子树数量不确定，所以没有与之对应的“完全树”，单纯依靠数组下标无法判断结点之间的逻辑关系。

可以发现树中，除了根结点外，其他任意结点都有且只有一个双亲结点（父结点）。

思路：用数组顺序存储各个结点。每个结点对应一个数组下标，在其中保存数据元素、指向双亲结点（父结点）的“指针”

在这里插入图片描述

树的存储1：双亲表示法

在这里插入图片描述

数组元素中，包含两个字段，第一个字段表示数据元素，第二个字段用一个int型变量指明双亲在数组中的下标是多少。
用刚才定义的结构体声明一个数组。
最后记录结点的总数。

拓展：双亲表示法存储“森林”

在这里插入图片描述

双亲表示法的优缺点

在这里插入图片描述

优点：找双亲（父结点）好
缺点：找孩子难，要遍历整个数组
应用场景：找父亲多，找孩子少，Eg.并查集

树的存储2：孩子表示法

在这里插入图片描述

在每个数组在链表元素中，保留一个链表头指针，如果其有孩子，在链表中保存所有孩子结点的编号

在这里插入图片描述

孩子表示法是顺序存储+链式存储结合
一个数组元素中包含data和一个链表CTNode的指针，链表结点中保存孩子的编号以及指向下一个链表结点的指针。
用刚才定义的结构体CTBox声明一个数组，存储各结点的信息。
并记录结点总数和根的位置。

拓展：孩子表示法存储“森林”

在这里插入图片描述

用孩子表示法存储森林，需要记录多个根的位置

孩子表示法的优缺点

在这里插入图片描述

优点：找孩子好
缺点：找双亲（父结点）难，要遍历整个数组
应用场景：找孩子多，找父亲少，Eg.服务流程树【办理业务请按1】

树的存储3：孩子兄弟表示法

在这里插入图片描述

链式实现
结构体包含数据，和两个指针，第一个指针指向第一个孩子，第二个指针指向右边一个兄弟【类似二叉树结点的定义】
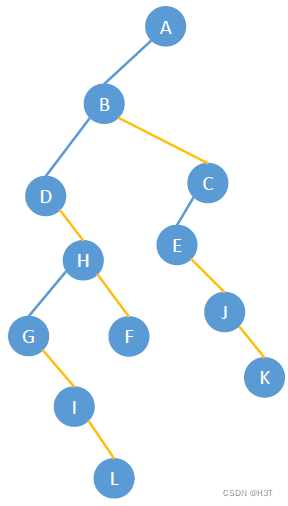
采用二叉链表实现

在这里插入图片描述

根结点是A，左指针指向B，右指针指向NULL；
C是B的右边第一个兄弟结点，连到B的右指针，D结点连到C的右指针；
E是B的第一个孩子，连到B的左指针；
F是E的右边第一个兄弟结点，连到E的右指针，G结点连到F的右指针，H连到G的右指针，I连到H的右指针，J连到I的右指针；
K是E的第一个孩子，连到E的左指针。

孩子兄弟表示法形态和二叉树类似。

拓展：孩子兄弟表示法存储“森林”

在这里插入图片描述

把树根C看做B的兄弟，连到B右指针上，以此类推。

5.4.2 树、森林与二叉树的转化

在这里插入图片描述

树->二叉树的转换

用孩子兄弟表示法存储树或者森林的时候会呈现出和二叉树类似的形态。
树、森林与二叉树的转换本质上就是画出用孩子兄弟表示法表示的树和森林。

在这里插入图片描述

树 -> 二叉树转换技巧：
① 先在二叉树中，画一个根结点。
② 按**“树的层序”**依次处理每个结点。

处理一个结点的方法是：如果当前处理的结点在树中有孩子，就把所有孩子结点“用右指针串成糖葫芦”，并在二叉树中把第一个孩子挂在当前结点的左指针下方

Eg1：

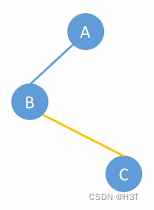
A结点：

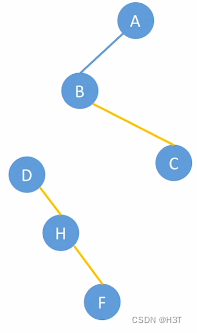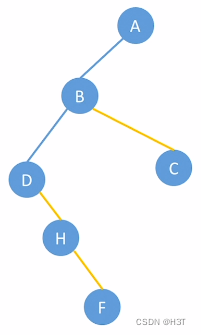
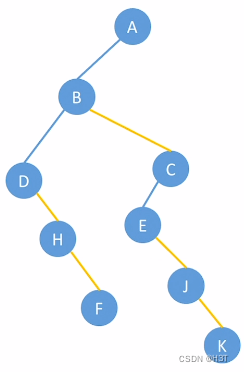
在这里插入图片描述----->在这里插入图片描述

B结点：
在这里插入图片描述----->在这里插入图片描述

C结点：
在这里插入图片描述

H结点：
在这里插入图片描述

Eg2.
在这里插入图片描述

森林->二叉树的转换

在这里插入图片描述
思路同上。
注意，第一步：森林中各树的根结点视为兄弟，用右指针串起来。
在这里插入图片描述
Eg2.

加粗样式

二叉树->树的转换

在这里插入图片描述
还原A结点：
在这里插入图片描述
以此类推还原。

Eg2.
在这里插入图片描述

二叉树->森林的转换

在这里插入图片描述
原理类似。
注意，先将根节点和一串右指针还原成多棵树的根结点。

Eg2.
在这里插入图片描述

5.4.3 树和森林的遍历

在这里插入图片描述

树的逻辑结构

在这里插入图片描述

有递归特性，可以用递归算法来实现对树的遍历

树的先根遍历

在这里插入图片描述

访问根结点visit(R)，接下来用while循环来检查其还有没有下一个没有被访问过的子树。
如果有，那么对子树也采取先根遍历的策略。

树的先根遍历序列与这棵树相应二叉树的先序序列相同。

树的后根遍历

在这里插入图片描述

原理类似，处理完所有子树时访问结点。
树的后根遍历序列与这棵树相应二叉树的后序序列相同。

树的层次遍历

在这里插入图片描述
实现思路和二叉树一样，用一个辅助队列来实现

根结点入队：
在这里插入图片描述
队头元素出队，该元素的孩子依次入队
在这里插入图片描述
重复该过程

尽量横向探索，也叫广度优先遍历。
那么先根遍历和后根遍历，也叫深度优先遍历。

森林的先序遍历

在这里插入图片描述

森林去掉根结点后各子树又组成森林，森林这种数据结构是和树相互递归定义的
可以用递归的思想来遍历森林

首先，访问森林中第一棵树的根结点B
先序遍历第一棵树中根结点的子树森林，E、F两棵树组成的森林
重复第一步，先访问森林中第一棵树的根结点E
遍历E的两个子树森林，即K、L两棵树组成的森林
遍历完K后，再遍历除了第一棵树K之后的剩余的树构成的森林，即L

效果等同于依次对各个树进行先根遍历
可以对各个子树进行一个先序遍历，然后排出一个完整的序列

另一种方法：转换成与之对应的二叉树：
在这里插入图片描述

效果等同于依次对二叉树的先序遍历

森林的中序遍历

在这里插入图片描述
同样可以转换成与之对应的二叉树：
在这里插入图片描述

效果等同于依次对二叉树的中序遍历

知识回顾与重要考点

5.4.1 树的存储结构

在这里插入图片描述

  • 双亲表示法：顺序存储，保存父结点下标，易找父，难找孩
  • 孩子表示法：顺序存储，保存孩子链表头指针（顺序+链式），易找孩，难找父
    在这里插入图片描述
  • 孩子兄弟表示法：二叉链表存储，左孩子右兄弟，形态上和二叉树类似

重要考点：树、森林与二叉树的转换

5.4.2 树、森林与二叉树的转化

在这里插入图片描述

  • 本质上就是用孩子兄弟表示法存储树或森林
  • 存储森林时，将每棵树的根结点视为兄弟
  • Tips：记“本质”，不记方法。方法只是表象，“本质”才是内核。

5.4.3 树和森林的遍历

在这里插入图片描述

  • 对森林的遍历可以转换成对二叉树的遍历

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/530808.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

【连续介质力学】张量的范数、各向同性和各向异性张量、同轴张量和极分解

【连续介质力学】张量的范数、各向同性和各向异性张量、同轴张量和极分解

张量的范数 张量的大小，使用Frobenius 范数： ∣ ∣ v ⃗ ∣ ∣ v ⃗ ⋅ v ⃗ v i v i （向量） ||\vec v|| \sqrt{\vec v \cdot \vec v} \sqrt{v_iv_i} （向量） ∣∣v ∣∣v ⋅v ​vi​vi​ ​&#xff…
阅读更多...
okhttp篇2：Dispatcher

okhttp篇2：Dispatcher

Dispatchers维护着一个线程池，3个双端队列，准备执行的AsynCall，正在执行的AsynCall，正在执行的同步Call（RealCall）。 同时规定每个Host最多同时请求5个Request，同时可最多执行64个Request。 p…
阅读更多...
玩转Google开源C++单元测试框架Google Test系列(gtest)之一 - 初识gtest

玩转Google开源C++单元测试框架Google Test系列(gtest)之一 - 初识gtest

一、前言 本篇将介绍一些gtest的基本使用，包括下载，安装，编译，建立我们第一个测试Demo工程，以及编写一个最简单的测试案例。 二、下载 如果不记得网址， 直接在google里搜gtest，第一个就是。目…
阅读更多...
Docker下Gitlab配置Let’s Encrypt证书

Docker下Gitlab配置Let’s Encrypt证书

Docker下Gitlab配置Let’s Encrypt证书 1 参考文档2 常见问题2.1 前置条件2.2 不支持ip2.3 重复签发2.4 外网无法访问 ※3 内网穿透配置（可选）4 Gitlab 创建并配置Let’s Encrypt证书4.1 开放Let’s Encrypt签发所需端口4.2 新增存储HTTPS证书文件夹4.3 …
阅读更多...
多态与虚函数（补）

多态与虚函数（补）

多态与虚函数（补） 静态联编与动态联编的深层次理解多态底层原理 示例示例一示例二示例三示例四 对象与内存虚析构函数构造函数为什么不能是虚函数？ 静态联编与动态联编的深层次理解 我们首先看下面一段代码 class object { private: int va…
阅读更多...
C learning_12 操作符前篇（算术操作符、移位操作符、位操作符、赋值操作符、单目操作符、关系操作符、逻辑操作符）

C learning_12 操作符前篇（算术操作符、移位操作符、位操作符、赋值操作符、单目操作符、关系操作符、逻辑操作符）

目录 算术操作符 移位操作符 移位规则 位操作符 交换两个整形变量的写法 赋值操作符 单目操作符 sizeof和数组的纠缠 和--运算符 多组输入的方案 关系操作符 逻辑操作符 算术操作符 -- 加法操作符（）：用于将两个值相加。 -- 减法操…
阅读更多...
Python爬虫（二）：Requests库

Python爬虫（二）：Requests库

所谓爬虫就是模拟客户端发送网络请求，获取网络响应，并按照一定的规则解析获取的数据并保存的程序。要说 Python 的爬虫必然绕不过 Requests 库。 1 简介 对于 Requests 库，官方文档是这么说的： Requests 唯一的一个非转基因的 P…
阅读更多...
存储知识点：RAID0、RAID1、RAID5、RAID10特点是什么？所需的硬盘数量分别为多少？

存储知识点：RAID0、RAID1、RAID5、RAID10特点是什么？所需的硬盘数量分别为多少？

RAID（Redundant Array of Independent Disks）是一种将多个独立的硬盘组合成一个逻辑磁盘的技术，目的是提高性能或容错能力。RAID有不同的级别，常见的有RAID0、RAID1、RAID5、RAID10等。下面我们来介绍这些级别的特点和所需的硬盘数…
阅读更多...
套接字编程简介

套接字编程简介

作者：V7 博客：https://www.jvmstack.cn 一碗鸡汤 少年辛苦终身事，莫向光阴惰寸功。 —— 杜荀鹤 Socket概述 在计算机中产生和接受IO流的数据源是多种多样的，在网络编程中，有一个特殊的数据源就是socket。通俗点soc…
阅读更多...
linux的系统日志

linux的系统日志

目录 一、日志文件的产生 二、日志文件存放在哪儿 （1）文本日志 （2）二进制日志 三、日志存放规则的配置文件 四、日志轮转 五、分析和监控日志 一、日志文件的产生 日志内容：内核、开机引导、守护进程启动运行的…
阅读更多...
华为和思科两种常见的网络设备如何进行ospf配置？

华为和思科两种常见的网络设备如何进行ospf配置？

概述 ospf（开放最短路径优先）是一种基于链路状态的动态路由协议，它可以在网络中自动发现和维护最优的路由路径。ospf广泛应用于大型和复杂的网络环境，因为它具有以下优点： 支持分层路由，可以将网络划分为…
阅读更多...
WebAssembly黑暗的一面

WebAssembly黑暗的一面

案例1：技术支持诈骗 什么是技术支持诈骗？ 技术支持诈骗是一种电话欺诈，其中诈骗者声称可以提供合法的技术支持服务。该骗局可能以陌生电话开始，骗子通常会声称来自合法的第三方的员工，如“微软”或“Windows部门”。他…
阅读更多...
YOLOv5实现目标分类计数并显示在图像上

YOLOv5实现目标分类计数并显示在图像上

有同学后台私信我，想用YOLOv5实现目标的分类计数，因此本文将在之前目标计数博客的基础上添加一些代码，实现分类计数。阅读本文前请先看那篇博客，链接如下： YOLOv5实现目标计数_Albert_yeager的博客 1. 分类实现 以co…
阅读更多...
web 实验一 HTML基本标签实验

web 实验一 HTML基本标签实验

实验原理 通过创建HTML5网页，验证form内多种元素标签及其属性的作用及意义。 实验目的 理解并掌握Form表单提交必须声明的内容 理解并掌握Input元素中多种类型属性的使用方法及使用场景 理解并掌握Label元素的使用方法 理解并掌握Datalist元素的使用方法 理解并掌握…
阅读更多...
软件测试学习——笔记一

软件测试学习——笔记一

一、软件和软件测试 1、软件和软件分类 （1）软件：程序、数据、文档——用户手册 （2）软件的分类 按层次划分：系统软件、应用软件按组织划分：开源软件（代码公开）、商业软…
阅读更多...
RSA 加密算法在C++中的实现 面向初学者（附代码）

RSA 加密算法在C++中的实现 面向初学者（附代码）

概述 博文的一，二部分为基础知识的铺垫。分别从密码学，数论两个方面为理解RSA算法做好了准备。第三部分是对RSA加密过程的具体介绍，主要涉及其密钥对（key-pair）的获取。前三个部分与编程实践无关，可以当作…
阅读更多...
C# | 内存池

C# | 内存池

内存池 文章目录 内存池前言什么是内存池内存池的优点内存池的缺点 实现思路示例代码结束语 前言 在上一篇文章中，我们介绍了对象池的概念和实现方式。对象池通过重复利用对象，避免了频繁地创建和销毁对象，提高了系统的性能和稳定性。 今天我…
阅读更多...
你真的了解索引吗

你真的了解索引吗

当我们学习存储算法和索引算法时，他们可以深入了解如何在系统中存储和查询数据。因为存储和查询数据是许多系统的核心功能之一，例如数据库、搜索引擎等。理解这些算法可以帮助程序员更好地设计和优化系统架构，提高系统的可扩展性、可用性和性…
阅读更多...
玩转Google开源C++单元测试框架Google Test系列(gtest)之二 - 断言

玩转Google开源C++单元测试框架Google Test系列(gtest)之二 - 断言

一、前言 这篇文章主要总结gtest中的所有断言相关的宏。 gtest中，断言的宏可以理解为分为两类，一类是ASSERT系列，一类是EXPECT系列。一个直观的解释就是： 1. ASSERT_* 系列的断言，当检查点失败时，退出当前…
阅读更多...
大数据之光：Apache Spark 实用指南 大数据实战详解【上进小菜猪大数据】

大数据之光：Apache Spark 实用指南 大数据实战详解【上进小菜猪大数据】

上进小菜猪，沈工大软件工程专业，爱好敲代码，持续输出干货。 本文将深入探讨Apache Spark作为一种强大的大数据处理框架的基本概念、特点和应用。我们将详细介绍Spark的核心组件，包括Spark Core、Spark SQL、Spark Streaming和Spa…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023