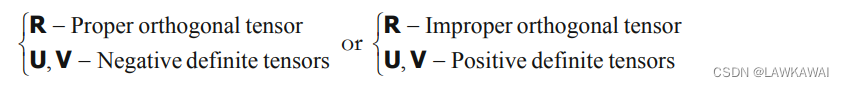张量的范数
张量的大小,使用Frobenius 范数:
∣
∣
v
⃗
∣
∣
=
v
⃗
⋅
v
⃗
=
v
i
v
i
(向量)
||\vec v|| = \sqrt{\vec v \cdot \vec v} = \sqrt{v_iv_i} (向量)
∣∣v∣∣=v⋅v=vivi(向量)
∣
∣
T
∣
∣
=
T
:
T
=
T
i
j
T
i
j
(二阶张量)
||T|| = \sqrt{ T:T} = \sqrt{T_{ij}T_{ij}} (二阶张量)
∣∣T∣∣=T:T=TijTij(二阶张量)
∣
∣
A
∣
∣
=
A
:
⋅
A
=
A
i
j
k
A
i
j
k
(三阶张量)
||A|| = \sqrt{ A:\cdot A} = \sqrt{A_{ijk}A_{ijk}} (三阶张量)
∣∣A∣∣=A:⋅A=AijkAijk(三阶张量)
∣
∣
C
∣
∣
=
C
:
:
C
=
C
i
j
k
l
C
i
j
k
l
(四阶张量)
||C|| = \sqrt{ C:: C} = \sqrt{C_{ijkl}C_{ijkl}} (四阶张量)
∣∣C∣∣=C::C=CijklCijkl(四阶张量)
在主空间,张量的特征值
T
1
,
T
2
,
T
3
T_1, T_2, T_3
T1,T2,T3,在主空间中:
∣
∣
T
∣
∣
=
T
:
T
=
T
i
j
T
i
j
=
T
1
2
+
T
2
2
+
T
3
3
=
I
T
2
−
2
I
I
T
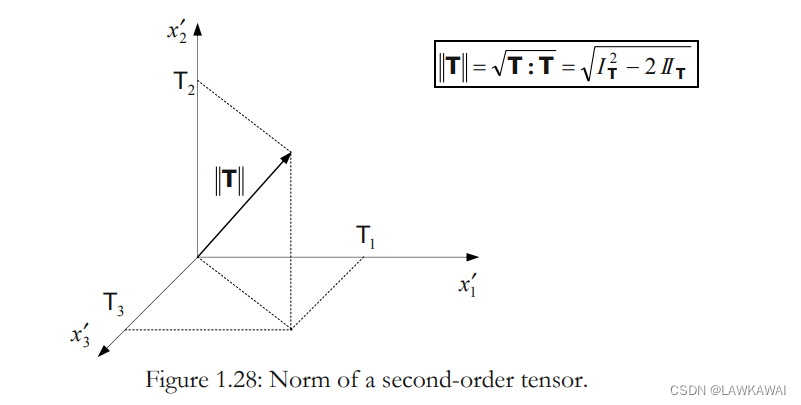
||T|| = \sqrt{ T:T} = \sqrt{T_{ij}T_{ij}} =\sqrt{T_1^2+T_2^2+T_3^3}=\sqrt{I_T^2-2II_T}
∣∣T∣∣=T:T=TijTij=T12+T22+T33=IT2−2IIT
所以,
∣
∣
T
∣
∣
||T||
∣∣T∣∣是一个不变量,
∣
∣
T
∣
∣
||T||
∣∣T∣∣表示的在主空间下主方向的长度
各向同性和各向异性张量
各向同性:在任意坐标系下,张量的分量都是一样的, T = T ′ T = T' T=T′
各向同性一阶张量:
在坐标系
(
x
1
,
x
2
,
x
3
)
(x_1, x_2, x_3)
(x1,x2,x3) 的分量
(
v
1
,
v
2
,
v
3
)
(v_1, v_2, v_3)
(v1,v2,v3)
在坐标系
(
x
1
′
,
x
2
′
,
x
3
′
)
(x_1', x_2', x_3')
(x1′,x2′,x3′) 的分量
(
v
1
′
,
v
2
′
,
v
3
′
)
(v_1', v_2', v_3')
(v1′,v2′,v3′)
根据变换定律:
v
⃗
=
v
i
e
^
i
=
v
j
′
e
^
j
′
⟹
v
i
′
=
a
i
j
v
j
\vec v = v_i \hat e_i = v_j' \hat e_j' \implies v_i' = a_{ij}v_j
v=vie^i=vj′e^j′⟹vi′=aijvj
由各向同性的定义,
v
i
=
v
j
′
v_i = v_j'
vi=vj′,那么有:
e
^
i
=
e
^
j
′
\hat e_i = \hat e_j'
e^i=e^j′
所以,要么是坐标系根本没有变换,要么满足各向同性的一阶张量只能是零向量 0 ⃗ \vec 0 0
各向同性二阶张量:
例子:单位张量
1
1
1,
δ
k
l
\delta_{kl}
δkl,根据二阶张量的变换定律:
δ
i
j
′
=
a
i
k
a
j
l
δ
k
l
=
a
i
k
a
j
k
=
δ
i
j
\delta_{ij}' = a_{ik}a_{jl}\delta_{kl}=a_{ik}a_{jk}=\delta_{ij}
δij′=aikajlδkl=aikajk=δij
所以,如果一个二阶张量是各向同性的,那么这个张量是球形张量
各向同性三阶张量:
Levi-Civita pseudo-tensor:
ϵ
i
j
k
\epsilon_{ijk}
ϵijk 不是真的张量
ϵ
i
j
k
′
=
a
i
l
a
j
m
a
k
n
ϵ
l
m
n
=
∣
A
∣
ϵ
i
j
k
=
ϵ
i
j
k
\epsilon _{ijk}'=a_{il}a_{jm}a_{kn}\epsilon_{lmn}=|A|\epsilon_{ijk}=\epsilon_{ijk}
ϵijk′=ailajmaknϵlmn=∣A∣ϵijk=ϵijk
各向同性四阶张量:
I
I
‾
‾
i
j
k
l
=
δ
i
j
δ
k
l
\overline{\overline{II}}_{ijkl} = \delta_{ij}\delta_{kl}
IIijkl=δijδkl
I
I
i
j
k
l
=
δ
i
k
δ
j
l
II_{ijkl} = \delta_{ik}\delta_{jl}
IIijkl=δikδjl
I
I
‾
i
j
k
l
=
δ
i
l
δ
j
k
\overline{II}_{ijkl} = \delta_{il}\delta_{jk}
IIijkl=δilδjk
所以,任意一个四阶各向同性张量可以表示为以上张量的线性组合:

问题1.37 四阶张量: C i j k l = λ δ i j δ k l + μ ( δ i k δ j l + δ i l δ j k ) C_{ijkl}=\lambda\delta_{ij}\delta_{kl}+\mu (\delta_{ik}\delta_{jl} + \delta_{il} \delta_{jk}) Cijkl=λδijδkl+μ(δikδjl+δilδjk),证明C是各向同性

同轴张量 Coaxial tensor
如果张量
T
T
T和
S
S
S有相同的特征向量,那么它们是同轴张量,也就是它们之间点积是可以交换的:
T
⋅
S
=
S
⋅
T
⟹
S
,
T
是同轴的
T \cdot S = S \cdot T \implies S,T 是同轴的
T⋅S=S⋅T⟹S,T是同轴的
如果张量
T
T
T和
S
S
S同轴且对称的,那么它们的谱表示:
T
=
∑
a
=
1
3
T
a
n
^
(
a
)
⨂
n
^
(
a
)
;
S
=
∑
a
=
1
3
S
a
n
^
(
a
)
⨂
n
^
(
a
)
;
T= \sum_{a=1}^3 T_a\hat n^{(a)}\bigotimes \hat n^{(a)} ; \quad S= \sum_{a=1}^3 S_a\hat n^{(a)}\bigotimes \hat n^{(a)} ;
T=a=1∑3Tan^(a)⨂n^(a);S=a=1∑3San^(a)⨂n^(a);
S
S
S和
S
−
1
S^{-1}
S−1是同轴的:
S
−
1
⋅
S
=
S
⋅
S
−
1
=
1
S^{-1}\cdot S = S \cdot S^{-1} = 1
S−1⋅S=S⋅S−1=1
S
=
∑
a
=
1
3
S
a
n
^
(
a
)
⨂
n
^
(
a
)
;
S
−
1
=
∑
a
=
1
3
1
S
a
n
^
(
a
)
⨂
n
^
(
a
)
;
S= \sum_{a=1}^3 S_a\hat n^{(a)}\bigotimes \hat n^{(a)} ; \quad S^{-1}= \sum_{a=1}^3 \frac{1}{S_a}\hat n^{(a)}\bigotimes \hat n^{(a)} ;
S=a=1∑3San^(a)⨂n^(a);S−1=a=1∑3Sa1n^(a)⨂n^(a);
如果
S
S
S和
T
T
T是同轴且对称的张量,那么
S
⋅
T
S \cdot T
S⋅T的结果是另一个对称张量:
T
⋅
S
=
S
⋅
T
⟹
T
⋅
S
−
S
⋅
T
=
0
⟹
T
⋅
S
−
(
T
⋅
S
)
T
=
0
⟹
2
(
T
⋅
S
)
s
k
e
e
w
=
0
T\cdot S = S \cdot T \\ \implies T \cdot S -S \cdot T = 0 \\ \implies T \cdot S -(T \cdot S)^T = 0 \\ \implies 2(T\cdot S)^{skeew} = 0
T⋅S=S⋅T⟹T⋅S−S⋅T=0⟹T⋅S−(T⋅S)T=0⟹2(T⋅S)skeew=0
所以张量的反对称部分是零张量,那么张量只由对称张量组成:
(
T
⋅
S
)
≡
(
T
⋅
S
)
s
y
m
(T \cdot S) \equiv (T \cdot S)^{sym}
(T⋅S)≡(T⋅S)sym
极分解
令 F F F是非奇异的二阶张量, det F ≠ 0 ⟹ ∃ F − 1 \det F \neq 0 \implies \exists F^{-1} detF=0⟹∃F−1
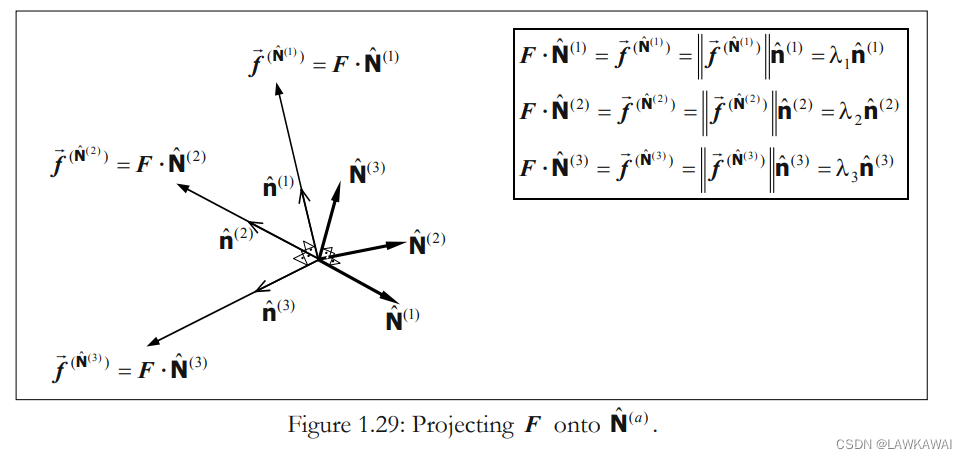
张量满足: F ⋅ N ^ = f ⃗ ( N ^ ) = ∣ ∣ f ⃗ ( N ^ ) ∣ ∣ n ^ = λ n ^ n ^ ≠ 0 ⃗ F \cdot \hat N = \vec f^{(\hat N)}=||\vec f^{(\hat N)}||\hat n = \lambda_{\hat n}\hat n \neq \vec 0 F⋅N^=f(N^)=∣∣f(N^)∣∣n^=λn^n^=0
给定一个正交基
N
^
(
a
)
\hat N^{(a)}
N^(a), 可得:

以上
F
F
F 的表达式并不是
F
F
F 的谱表示,因为
λ
a
\lambda_a
λa不是
F
F
F的特征值,并且
n
^
(
a
)
\hat n^{(a)}
n^(a)和
N
^
(
a
)
\hat N^{(a)}
N^(a)也都不是
F
F
F的特征向量
可以发现,对于任意正交基
N
^
(
a
)
\hat N^{(a)}
N^(a),新基
n
^
(
a
)
\hat n^{(a)}
n^(a) 不一定是正交的
现在,我们希望找到一个基
N
^
(
a
)
\hat N^{(a)}
N^(a),使得新基
n
^
(
a
)
\hat n^{(a)}
n^(a)是正交的,也就是:
f
⃗
(
N
^
(
1
)
)
⋅
f
⃗
(
N
^
(
2
)
)
=
0
f
⃗
(
N
^
(
2
)
)
⋅
f
⃗
(
N
^
(
3
)
)
=
0
f
⃗
(
N
^
(
3
)
)
⋅
f
⃗
(
N
^
(
1
)
)
=
0
\vec f^{(\hat N^{(1)})} \cdot \vec f^{(\hat N^{(2)})} = 0 \\ \vec f^{(\hat N^{(2)})} \cdot \vec f^{(\hat N^{(3)})} = 0 \\ \vec f^{(\hat N^{(3)})} \cdot \vec f^{(\hat N^{(1)})} = 0
f(N^(1))⋅f(N^(2))=0f(N^(2))⋅f(N^(3))=0f(N^(3))⋅f(N^(1))=0
那么我们根据正交变换 n ^ ( a ) = R ⋅ N ^ ( a ) \hat n^{(a)} = R \cdot \hat N^{(a)} n^(a)=R⋅N^(a) 来寻找一个空间,可以保证 n ^ ( a ) \hat n^{(a)} n^(a) 的正交性,因为正交变换既不改变向量之间的角度,也不改变其大小
所以,假设有一个从
N
^
(
a
)
\hat N^{(a)}
N^(a)到
n
^
(
a
)
\hat n^{(a)}
n^(a) 的变换,正交变换
n
^
(
a
)
=
R
⋅
N
^
(
a
)
\hat n^{(a)} = R \cdot \hat N^{(a)}
n^(a)=R⋅N^(a),那么:
F
=
∑
a
=
1
3
λ
a
n
^
(
a
)
⨂
N
^
(
a
)
=
∑
a
=
1
3
λ
a
R
⋅
N
^
(
a
)
⨂
N
^
(
a
)
=
R
⋅
∑
a
=
1
3
λ
a
N
^
(
a
)
⨂
N
^
(
a
)
=
R
⋅
U
F = \sum_{a =1}^3\lambda_a \hat n^{(a)}\bigotimes \hat N^{(a)} =\sum_{a =1}^3\lambda_a R \cdot \hat N^{(a)}\bigotimes \hat N^{(a)} \\ =R \cdot\sum_{a =1}^3\lambda_a \hat N^{(a)}\bigotimes \hat N^{(a)} = R \cdot U
F=a=1∑3λan^(a)⨂N^(a)=a=1∑3λaR⋅N^(a)⨂N^(a)=R⋅a=1∑3λaN^(a)⨂N^(a)=R⋅U
F = R ⋅ U ⟹ U = R T ⋅ F F = R \cdot U \implies U = R^T \cdot F F=R⋅U⟹U=RT⋅F
其中, U = N ^ ( a ) ⨂ N ^ ( a ) U = \hat N^{(a)}\bigotimes \hat N^{(a)} U=N^(a)⨂N^(a),是一个对称张量, U = U T U = U^T U=UT
反过来,
N
^
(
a
)
=
R
T
⋅
n
^
(
a
)
=
n
^
(
a
)
⋅
R
\hat N^{(a)} = R^T \cdot \hat n^{(a)} = \hat n^{(a)} \cdot R
N^(a)=RT⋅n^(a)=n^(a)⋅R, 那么:
F
=
∑
a
=
1
3
λ
a
n
^
(
a
)
⨂
N
^
(
a
)
=
∑
a
=
1
3
λ
a
n
^
(
a
)
⨂
n
^
(
a
)
⋅
R
=
V
⋅
R
F = \sum_{a =1}^3\lambda_a \hat n^{(a)}\bigotimes \hat N^{(a)} =\sum_{a =1}^3\lambda_a \hat n^{(a)}\bigotimes \hat n^{(a)} \cdot R \\ =V \cdot R
F=a=1∑3λan^(a)⨂N^(a)=a=1∑3λan^(a)⨂n^(a)⋅R=V⋅R
F = V ⋅ R ⟹ V = F ⋅ R T F = V \cdot R \implies V = F \cdot R^T F=V⋅R⟹V=F⋅RT
其中, V = n ^ ( a ) ⨂ n ^ ( a ) V = \hat n^{(a)}\bigotimes \hat n^{(a)} V=n^(a)⨂n^(a)
U U U 和 V V V有相同的特征值,但不同的特征向量
定义极分解:
F
=
R
⋅
U
=
V
⋅
R
T
(极分解)
\boxed{F = R \cdot U = V \cdot R^T} (极分解)
F=R⋅U=V⋅RT(极分解)
对
F
T
F^T
FT和
F
F
F进行点积:
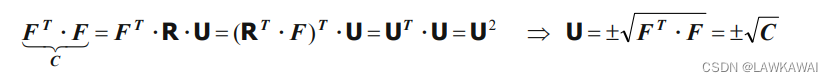
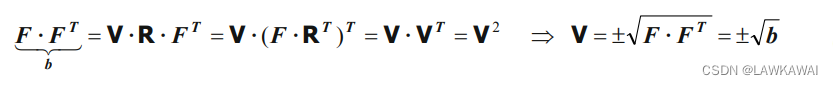
NOTE: 由于 det F ≠ 0 \det F \neq 0 detF=0,所以 C C C 和 b b b是正定对称张量,表示 C C C和 b b b的特征值是正实数,但是 det F ≠ 0 \det F \neq 0 detF=0 有以下两种情况:
- 如果
det
F
>
0
\det F > 0
detF>0
det F = det R det U = det V det R T > 0 \det F = \det R \det U = \det V \det R^T > 0 detF=detRdetU=detVdetRT>0,那么:

- 如果
det
F
<
0
\det F < 0
detF<0
det F = det R det U = det V det R T < 0 \det F = \det R \det U = \det V \det R^T < 0 detF=detRdetU=detVdetRT<0,那么: