评估对比

我们现在对 t=25 的生存率得出了一个新的估计值，为0.56。现在，让我们将其与之前所做的估计进行比较。

当我们假设所有患者在他们截尾时间立即死亡时，我们获得了一个低生存概率为0.29。而在另一极端，如果我们假设他们永久存活时，生存率估计值为0.71。

我们还研究了如果我们可以访问数据中的真实事件发生时间会发生什么情况，虽然这通常是不可能观察到的，但在这个假想的场景中，我们可以联系患者并找出事件发生的时间。我们有一个真实的估计值可以基于此进行计算，真实概率为0.57。

我们可以看到，我们的新估计（基于链式法则）更接近于真实估计，比我们两个极端观测得到的更接近。因此，我们已经学习了如何在存在删失的情况下估计生存概率。

现在我们已经学习了如何在存在删失的情况下估计超过25个月的生存概率，让我们看看如何将其推广到任何时间点 小t。

在这里，我们可以表示任何时间点t的生存概率为一个乘积。我们可以在i处开始，从零时刻一直延续到时间点t，然后在其中我们会有1减去事件时间在i时发生的概率

现在，我们已经学会了如何直接从数据中估计该数量作为在时间i内死亡的患者数和在i时刻已知存活的人数之比。我们可以用di来简写分子，ni来简写分母，这带来了生存函数的表达式
即：${\prod }_{i=0}^{t}1-\frac{d_i}{n_i}$

Kaplan Meier估计

这就是Kaplan-Meier估计，它可以让我们从种群中得到一个生存函数。因此，我们所做的是，我们能够使用生存数据来表示种群，我们根据这些数据建立了Kaplan-Meier生存模型。

这个模型的关键是，我们估计的生存函数适用于人群中的所有患者；它并不是针对特定患者的。我们可以计算两个不同种群的Kaplan-Meier曲线或生存曲线，并将其相互比较。

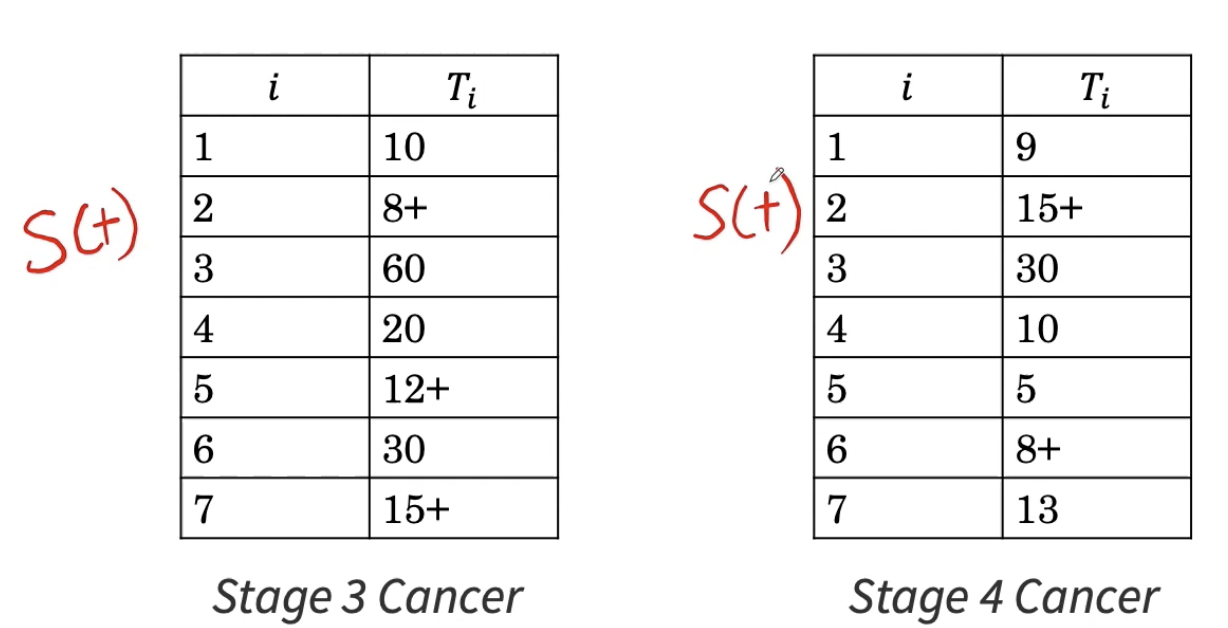
例如，我们想知道3期癌症和4期癌症患者的预后。我们可以使用Kaplan-Meier估计建立两个独立的生存函数，并且我们可以在同一图上绘制生存的Kaplan-Meier估计。

这里用橙色表示第4期生存率的估计图，用蓝色表示第3期的生存率。因此，如果你想告诉人群中任何患者的预后或生存概率，我们只需在给定的时间，比方说50，查询当时的生存概率或y值，就可以知道两个人群中患者的生存概率的差异。

我们已经看到了如何使用Kaplan-Meier估计来获得生存曲线。本周，我们讨论了生存分析的问题。使用生存建模，我们看到了我们现在如何对任何时间t的生存进行建模。我们研究了生存分析中数据的一个关键特征：右删失。

正如我们所看到的，右删失是一种数据缺失问题，因为研究终止，或者因为患者在经历事件之前离开了研究，所以没有观察到事件发生的时间。我们最后研究了Kaplan-Meier估计器，该估计器考虑了删失来估计整个种群的生存函数。

我们还没有研究的是如何通过考虑患者的特殊情况来对患者的生存率进行个性化估计。下周，我们将研究建立和评估这种个性化生存预测模型的策略。

本次课完有个小练习，一共8个题来检验一下学习成果吧

结束此周的学习之后，将通过两个编程作业来进行总结回顾

see you in next homework~~

文章持续更新，可以关注微信公众号【医学图像人工智能实战营】获取最新动态，一个关注于医学图像处理领域前沿科技的公众号。坚持已实践为主，手把手带你做项目，打比赛，写论文。凡原创文章皆提供理论讲解，实验代码，实验数据。只有实践才能成长的更快，关注我们，一起学习进步~

我是Tina, 我们下篇博客见~

白天工作晚上写文，呕心沥血

觉得写的不错的话最后，求点赞，评论，收藏。或者一键三连