本文已收录到 AndroidFamily,技术和职场问题,请关注公众号 [彭旭锐] 提问。
- 往期回顾:LeetCode 双周赛第 104 场 · 流水的动态规划,铁打的结构化思考
周赛概览
T1. 找出转圈游戏输家(Easy)
- 标签:模拟、计数
T2. 相邻值的按位异或(Medium)
- 标签:模拟、数学、构造
T3. 矩阵中移动的最大次数(Medium)
- 标签:图、BFS、DFS、动态规划
T4. 统计完全连通分量的数量(Medium)
- 标签:图、BFS、DFS、并查集
T1. 找出转圈游戏输家(Easy)
https://leetcode.cn/problems/find-the-losers-of-the-circular-game/
题解(模拟)
简单模拟题。
使用标记数组标记接触到球的玩家,再根据标记数组输出结果:
class Solution {
fun circularGameLosers(n: Int, k: Int): IntArray {
val visit = BooleanArray(n)
var i = 0
var j = 1
var cnt = n
while (!visit[i]) {
visit[i] = true
i = (i + j++ * k) % n
cnt--
}
val ret = IntArray(cnt)
var k = 0
for (i in visit.indices) {
if(!visit[i]) ret[k++] = i + 1
}
return ret
}
}
复杂度分析:
- 时间复杂度: O ( n ) O(n) O(n) 每位玩家最多标记一次和检查一次;
- 空间复杂度: O ( n ) O(n) O(n) 标记数组空间。
T2. 相邻值的按位异或(Medium)
https://leetcode.cn/problems/neighboring-bitwise-xor/
预备知识
记 ⊕ 为异或运算,异或运算满足以下性质:
- 基本性质:x ⊕ y = 0
- 交换律:x ⊕ y = y ⊕ x
- 结合律:(x ⊕ y) ⊕ z = x ⊕ (y ⊕ z)
- 自反律:x ⊕ y ⊕ y = x
题解一(模拟)
由于每一位 derived[i] 可以由 original[i] ⊕ original[i + 1] 获得,我们可以令原始的 original[0] 为 0,再按顺序递推到 original[n](循环数组),最后再检查 original[0] 和 original[n] 是否相同。如果不同,说明 derived 数组是不可构造的。
class Solution {
fun doesValidArrayExist(derived: IntArray): Boolean {
var pre = 0
for ((i,d) in derived.withIndex()) {
if (d == 1) pre = pre xor 1
}
return pre == 0
}
}
复杂度分析:
- 时间复杂度: O ( n ) O(n) O(n) 其中 n 为 derived 数组的长度;
- 空间复杂度:仅使用常量级别空间。
题解二(数学)
继续挖掘问题的数学性质:
- 题目要求: d e r i v e d [ i ] = o r i g i n a l [ i ] ⊕ o r i g i n a l [ i + 1 ] derived[i] = original[i] ⊕ original[i + 1] derived[i]=original[i]⊕original[i+1]
- 根据自反律(两边异或 original[i]): o r i g i n a l [ i + 1 ] = d e r i v e d [ i ] ⊕ o r i g i n a l [ i ] original[i + 1] = derived[i] ⊕ original[i] original[i+1]=derived[i]⊕original[i]、 o r i g i n a l [ i + 2 ] = d e r i v e d [ i + 1 ] ⊕ o r i g i n a l [ i + 1 ] original[i + 2] = derived[i + 1] ⊕ original[i + 1] original[i+2]=derived[i+1]⊕original[i+1]
- 根据递推关系有 o r i g i n a l [ n − 1 ] = d e r i v e d [ n − 2 ] ⊕ d e r i v e d [ n − 1 ] … d e r i v e d [ 0 ] ⊕ o r i g i n a l [ 0 ] original[n - 1] = derived[n - 2] ⊕ derived[n - 1]… derived[0] ⊕ original[0] original[n−1]=derived[n−2]⊕derived[n−1]…derived[0]⊕original[0]
- 题目要求: o r i g i n a l [ 0 ] ⊕ o r i g i n a l [ n − 1 ] = d e r i v e d [ n − 1 ] original[0] ⊕ original[n - 1] = derived[n-1] original[0]⊕original[n−1]=derived[n−1]
- 联合两式: o r i g i n a l [ 0 ] = o r i g i n a l [ 0 ] ⊕ d e r i v e d [ n − 1 ] ⊕ d e r i v e d [ n − 1 ] … d e r i v e d [ 0 ] ⊕ o r i g i n a l [ 0 ] original[0] = original[0] ⊕ derived[n-1] ⊕ derived[n - 1]… derived[0] ⊕ original[0] original[0]=original[0]⊕derived[n−1]⊕derived[n−1]…derived[0]⊕original[0],即 0 = d e r i v e d [ n − 1 ] ⊕ d e r i v e d [ n − 1 ] … d e r i v e d [ 0 ] 0 = derived[n-1] ⊕ derived[n - 1]… derived[0] 0=derived[n−1]⊕derived[n−1]…derived[0]
根据结论公式模拟即可:
class Solution {
fun doesValidArrayExist(derived: IntArray): Boolean {
// return derived.fold(0) {acc, e -> acc xor e} == 0
return derived.reduce {acc, e -> acc xor e} == 0
}
}
复杂度分析:
- 时间复杂度: O ( n ) O(n) O(n) 其中 n 为 derived 数组的长度;
- 空间复杂度:仅使用常量级别空间。
T3. 矩阵中移动的最大次数(Medium)
https://leetcode.cn/problems/maximum-number-of-moves-in-a-grid/
题目描述
给你一个下标从 0 开始、大小为 m x n 的矩阵 grid ,矩阵由若干 正 整数组成。
你可以从矩阵第一列中的 任一 单元格出发,按以下方式遍历 grid :
- 从单元格
(row, col)可以移动到(row - 1, col + 1)、(row, col + 1)和(row + 1, col + 1)三个单元格中任一满足值 严格 大于当前单元格的单元格。
返回你在矩阵中能够 移动 的 最大 次数。
示例 1:
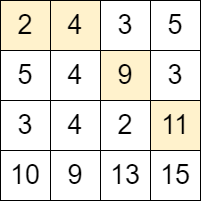
输入:grid = [[2,4,3,5],[5,4,9,3],[3,4,2,11],[10,9,13,15]]
输出:3
解释:可以从单元格 (0, 0) 开始并且按下面的路径移动:
- (0, 0) -> (0, 1).
- (0, 1) -> (1, 2).
- (1, 2) -> (2, 3).
可以证明这是能够移动的最大次数。
示例 2:
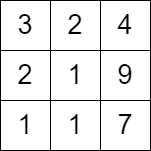
输入:grid = [[3,2,4],[2,1,9],[1,1,7]]
输出:0
解释:从第一列的任一单元格开始都无法移动。
提示:
m == grid.lengthn == grid[i].length2 <= m, n <= 10004 <= m * n <= 1051 <= grid[i][j] <= 106
问题结构化
1、概括问题目标
计算可移动的最大次数,也可以理解为可访问距离 - 1。
2、分析问题要件
在每次移动操作中,可以移动到右边一列的最近三行位置(i-1, i, j+1)且要求数字严格大于当前位置。
3、提高抽象程度
- 子问题:我们发现每次移动后,可移动次数就是在新位置可移动次数 + 1,这是一个与原问题相似但规模更小的子问题;
- 是否为决策问题?由于每次移动最多有三个位置选择,因此这是决策问题。
4、具体化解决手段
- 手段 1(记忆化递归):定义 dfs(i, j) 表示从 grid[i][j] 开始的最大移动次数,那么有 dfs(i, j)= mas{dfs(i-1, j+1), dfs(i, j+1), dfs(i+1, j+1)};
- 手段 2(递推):在记忆化递归中我们是在「归」的过程中合并子问题的解,由于递归的方向是验证矩阵从上到下,从左到右的,我们可以消除「递」的过程而只保留「归」的过程,将递归转换为递推;
- 手段 3(BFS):由于可移动次数取决于最多可以移动到的列号,我们可以用 BFS / DFS 搜索最远可以访问的列号。
题解一(记忆化递归)
根据「手段 1」模拟即可:
- 递归函数:dfs(i, j)= mas{dfs(i-1, j+1), dfs(i, j+1), dfs(i+1, j+1)}
- 起始状态:dfs(i, 0)
- 边界条件:dfs(i, j) = 0
class Solution {
val directions = arrayOf(intArrayOf(-1, 1), intArrayOf(0, 1), intArrayOf(1, 1)) // 右上、右、右下
private val memo = HashMap<Int, Int>()
private val U = 1001
fun maxMoves(grid: Array<IntArray>): Int {
var ret = 0
for (i in 0 until grid.size) {
ret = Math.max(ret, dfs(grid, i, 0))
}
return ret - 1
}
private fun dfs(grid: Array<IntArray>, i: Int, j: Int): Int {
val n = grid.size
val m = grid[0].size
val key = i * U + j
if (memo.contains(key)) return memo[key]!!
// 枚举选项
var maxChoice = 0
for (direction in directions) {
val newI = i + direction[0]
val newJ = j + direction[1]
if (newI < 0 || newI >= n || newJ < 0 || newJ >= m || grid[i][j] >= grid[newI][newJ]) continue
maxChoice = Math.max(maxChoice, dfs(grid, newI, newJ))
}
memo[key] = maxChoice + 1
return maxChoice + 1
}
}
复杂度分析:
- 时间复杂度: O ( n m ) O(nm) O(nm) 总共有 nm 个子问题,每个子问题枚举 3 个选项时间复杂度是 O(1);
- 空间复杂度: O ( n m ) O(nm) O(nm) 备忘录空间。
题解二(递推)
消除「递」的过程而只保留「归」的过程,将递归转换为递推:
class Solution {
fun maxMoves(grid: Array<IntArray>): Int {
val n = grid.size
val m = grid[0].size
val step = Array(n) { IntArray(m) }
for (i in 0 until n) step[i][0] = 1
var ret = 0
// 按列遍历
for(j in 1 until m) {
for(i in 0 until n) {
for(k in Math.max(0, i - 1) .. Math.min(n - 1,i + 1)) {
if (step[k][j - 1] > 0 && grid[i][j] > grid[k][j - 1]) step[i][j] = Math.max(step[i][j], step[k][j - 1] + 1)
}
ret = Math.max(ret, step[i][j])
}
}
return Math.max(ret - 1, 0)
}
}
另外,我们也可以用滚动数组优化空间:
class Solution {
fun maxMoves(grid: Array<IntArray>): Int {
val n = grid.size
val m = grid[0].size
var step = IntArray(n) { 1 }
var ret = 0
// 按列遍历
for(j in 1 until m) {
val newStep = IntArray(n) { 0 } // 不能直接在 step 数组上修改
for(i in 0 until n) {
for(k in Math.max(0, i - 1) .. Math.min(n - 1,i + 1)) {
if (step[k] > 0 && grid[i][j] > grid[k][j - 1]) newStep[i] = Math.max(newStep[i], step[k] + 1)
}
ret = Math.max(ret, newStep[i])
}
step = newStep
}
return Math.max(ret - 1, 0)
}
}
复杂度分析:
- 时间复杂度: O ( n m ) O(nm) O(nm)
- 空间复杂度: O ( n ) O(n) O(n)
题解三(BFS)
按照广度优先搜索,使用队列维护可以访问的节点,再使用该节点探测下一层可到达的位置并入队。
class Solution {
fun maxMoves(grid: Array<IntArray>): Int {
val n = grid.size
val m = grid[0].size
// 行号
var queue = LinkedList<Int>()
for (i in 0 until n) {
queue.offer(i)
}
// 访问标记
val visit = IntArray(n) { -1 }
// 枚举列
for (j in 0 until m - 1) {
val newQueue = LinkedList<Int>() // 不能直接在 step 数组上修改
for (i in queue) {
for (k in Math.max(0, i - 1)..Math.min(n - 1, i + 1)) {
if (visit[k] < j && grid[k][j + 1] > grid[i][j]) {
newQueue.offer(k)
visit[k] = j
}
}
}
queue = newQueue
if (queue.isEmpty()) return j
}
return m - 1
}
}
复杂度分析:
- 时间复杂度: O ( n m ) O(nm) O(nm)
- 空间复杂度: O ( n ) O(n) O(n)
相似问题:
- 62. 不同路径
- 63. 不同路径 II
T4. 统计完全连通分量的数量(Medium)
https://leetcode.cn/problems/count-the-number-of-complete-components/
问题描述
给你一个整数 n 。现有一个包含 n 个顶点的 无向 图,顶点按从 0 到 n - 1 编号。给你一个二维整数数组 edges 其中 edges[i] = [ai, bi] 表示顶点 ai 和 bi 之间存在一条 无向 边。
返回图中 完全连通分量 的数量。
如果在子图中任意两个顶点之间都存在路径,并且子图中没有任何一个顶点与子图外部的顶点共享边,则称其为 连通分量 。
如果连通分量中每对节点之间都存在一条边,则称其为 完全连通分量 。
示例 1:
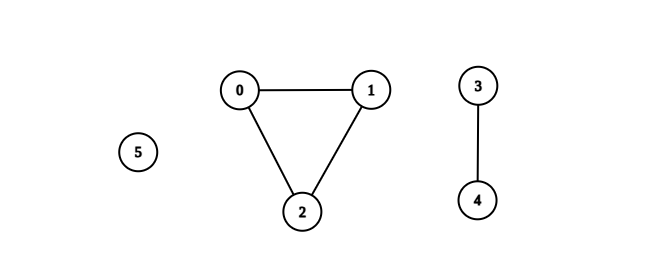
输入:n = 6, edges = [[0,1],[0,2],[1,2],[3,4]]
输出:3
解释:如上图所示,可以看到此图所有分量都是完全连通分量。
示例 2:
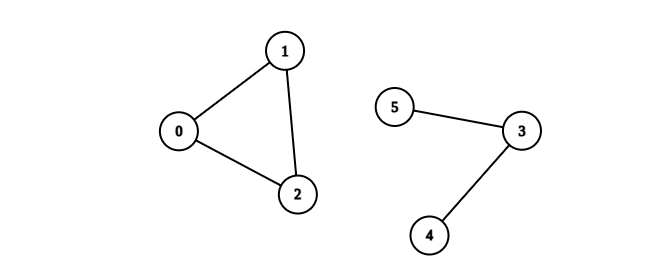
输入:n = 6, edges = [[0,1],[0,2],[1,2],[3,4],[3,5]]
输出:1
解释:包含节点 0、1 和 2 的分量是完全连通分量,因为每对节点之间都存在一条边。
包含节点 3 、4 和 5 的分量不是完全连通分量,因为节点 4 和 5 之间不存在边。
因此,在图中完全连接分量的数量是 1 。
提示:
1 <= n <= 500 <= edges.length <= n * (n - 1) / 2edges[i].length == 20 <= ai, bi <= n - 1ai != bi- 不存在重复的边
预备知识 - 完全图
完全图中每对不同的顶点之间都恰连有一条边相连,n 个节点的完全图有 n*(n − 1) / 2 条边。
问题分析
这道题是比较直接的岛屿 / 连通分量问题,我们直接跑 DFS / BFS / 并查集,计算每个连通分量的节点数和边数是否平衡。
如果连通分量是完全图,那么节点数 v 和边数 e 满足 e == v * (v - 2) / 2
题解一(DFS)
枚举每个节点跑 DFS,统计相同连通分量的节点数 v 和节点数 e,由于在遍历的时候,同一条边会在两个节点上重复统计,所以判断连通分量是否为完全图的公式调整为 e == v * (v - 2)。
class Solution {
fun countCompleteComponents(n: Int, edges: Array<IntArray>): Int {
// 建图(邻接表)
val graph = Array(n) { mutableListOf<Int>() }
for (edge in edges) {
graph[edge[0]].add(edge[1])
graph[edge[1]].add(edge[0]) // 无向边
}
// 标记数组
val visit = BooleanArray(n)
// 枚举
var ret = 0
for (i in 0 until n) {
if (visit[i]) continue
val cnt = IntArray(2) // v, e
dfs(graph, visit, i, cnt)
if (cnt[1] == cnt[0] * (cnt[0] - 1)) ret++
}
return ret
}
private fun dfs(graph: Array<out List<Int>>, visit: BooleanArray, i: Int, cnt: IntArray) {
visit[i] = true
cnt[0] += 1 // 增加节点
cnt[1] += graph[i].size // 增加边(会统计两次)
for (to in graph[i]) {
if (!visit[to]) dfs(graph, visit, to, cnt)
}
}
}
复杂度分析:
- 时间复杂度: O ( n + m ) O(n + m) O(n+m) 其中 n 为节点数,m 为 edges 的长度;
- 空间复杂度:图空间 O ( m ) O(m) O(m),标记数组空间 O ( n ) O(n) O(n)。
题解二(BFS)
附赠一份 BFS 代码:
class Solution {
fun countCompleteComponents(n: Int, edges: Array<IntArray>): Int {
// 建图(邻接表)
val graph = Array(n) { mutableListOf<Int>() }
for (edge in edges) {
graph[edge[0]].add(edge[1])
graph[edge[1]].add(edge[0]) // 无向边
}
// 标记数组
val visit = BooleanArray(n)
// 枚举
var ret = 0
for (i in 0 until n) {
if (visit[i]) continue
var v = 0
var e = 0
// BFS
var queue = LinkedList<Int>()
queue.offer(i)
visit[i] = true
while (!queue.isEmpty()) {
val temp = queue
queue = LinkedList<Int>()
for (j in temp) {
v += 1 // 增加节点
e += graph[j].size // 增加边(会统计两次)
for (to in graph[j]) {
if (!visit[to]) {
queue.offer(to)
visit[to] = true
}
}
}
}
if (e == v * (v - 1)) ret++
}
return ret
}
}
复杂度分析:
- 时间复杂度: O ( n + m ) O(n + m) O(n+m) 其中 n 为节点数,m 为 edges 的长度;
- 空间复杂度:图空间、标记数组空间和队列空间。
题解三(并查集)
附赠一份并查集代码:
class Solution {
fun countCompleteComponents(n: Int, edges: Array<IntArray>): Int {
val uf = UnionFind(n)
for (edge in edges) {
uf.union(edge[0], edge[1])
}
return uf.count()
}
private class UnionFind(n: Int) {
private val parent = IntArray(n) { it }
private val rank = IntArray(n)
private val e = IntArray(n)
private val v = IntArray(n) { 1 }
fun find(x: Int): Int {
// 路径压缩
var a = x
while (parent[a] != a) {
parent[a] = parent[parent[a]]
a = parent[a]
}
return a
}
fun union(x: Int, y: Int) {
val rootX = find(x)
val rootY = find(y)
if (rootX == rootY) {
e[rootX]++
} else {
// 按秩合并
if (rank[rootX] < rank[rootY]) {
parent[rootX] = rootY
e[rootY] += e[rootX] + 1 // 增加边
v[rootY] += v[rootX] // 增加节点
} else if (rank[rootY] > rank[rootX]) {
parent[rootY] = rootX
e[rootX] += e[rootY] + 1
v[rootX] += v[rootY]
} else {
parent[rootY] = rootX
e[rootX] += e[rootY] + 1
v[rootX] += v[rootY]
rank[rootX]++
}
}
}
// 统计连通分量
fun count(): Int {
return parent.indices.count { parent[it] == it && v[it] * (v[it] - 1) / 2 == e[it] }
}
}
}
复杂度分析:
- 时间复杂度: O ( n + a m ) O(n + am) O(n+am) 其中 n 为节点数,m 为 edges 的长度,其中 a a a 为反阿克曼函数。
- 空间复杂度: O ( n ) O(n) O(n) 并查集空间。
往期回顾
- LeetCode 单周赛第 344 场 · 手写递归函数的通用套路
- LeetCode 单周赛第 343 场 · 结合「下一个排列」的贪心构造问题
- LeetCode 双周赛第 104 场 · 流水的动态规划,铁打的结构化思考
- LeetCode 双周赛第 103 场 · 区间求和的树状数组经典应用








![[刷题]贪心入门](https://img-blog.csdnimg.cn/1c2ea4f5788f4b83a7aa13c3a3604490.png)