分子模拟力场
AMBER力场是在生物大分子的模拟计算领域有着广泛应用的一个分子力场。开发这个力场的是Peter Kollman课题组,最初AMBER力场是专门为了计算蛋白质和核酸体系而开发的,计算其力场参数的数据均来自实验值,后来随着AMBER力场的广泛应用,包括Kollman在内的很多课题组对AMBER力场的内容不断进行丰富,逐渐开发出了一个可以用于生物大分子、有机小分子和高分子模拟计算的力场体系。但是总体来讲,AMBER力场的优势在于对生物大分子的计算,其对小分子体系的计算结果常常不能令人满意。
AMBER力场的势能函数形势较为简单,所需参数不多,计算量也比较小,这是这个力场的一大特色,但也在一定程度上限制了这个力场的扩展性。
本力场用谐振子模型计算键长伸缩能和键角弯转能,用傅里叶级数的形式来描述二面角扭转能,选用Lennard-Jones势来模拟范德华作用;用库仑公式来描述静电相互作用。其势能表达式为:
V
(
r
N
)
=
∑
bonds
1
2
k
b
(
l
−
l
0
)
2
+
∑
angles
1
2
k
a
(
θ
−
θ
0
)
2
+
∑
torsions
1
2
V
n
[
1
+
cos
(
n
ω
−
γ
)
]
+
∑
j
=
1
N
−
1
∑
i
=
j
+
1
N
{
4
ϵ
i
,
j
[
(
σ
i
j
r
i
j
)
12
−
(
σ
i
j
r
i
j
)
6
]
+
q
i
q
j
4
π
ϵ
0
r
i
j
}
\begin{aligned} V_{\left(r^N\right)} & =\sum_{\text {bonds }} \frac{1}{2} k_b\left(l-l_0\right)^2+\sum_{\text {angles }} \frac{1}{2} k_a\left(\theta-\theta_0\right)^2+\sum_{\text {torsions }} \frac{1}{2} V_n[1+\cos (n \omega-\gamma)] \\ & +\sum_{j=1}^{N-1} \sum_{i=j+1}^N\left\{4 \epsilon_{i, j}\left[\left(\frac{\sigma_{i j}}{r_{i j}}\right)^{12}-\left(\frac{\sigma_{i j}}{r_{i j}}\right)^6\right]+\frac{q_i q_j}{4 \pi \epsilon_0 r_i j}\right\} \end{aligned}
V(rN)=bonds ∑21kb(l−l0)2+angles ∑21ka(θ−θ0)2+torsions ∑21Vn[1+cos(nω−γ)]+j=1∑N−1i=j+1∑N{4ϵi,j[(rijσij)12−(rijσij)6]+4πϵ0rijqiqj}
分子力场成键模型
键长
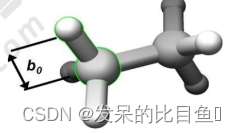
E
r
=
∑
Rands
K
r
2
(
r
i
j
−
r
i
j
′
)
2
E_r=\sum_{\text {Rands }} \frac{K_r}{2}\left(r_{i j}-r_{i j}^{\prime}\right)^2
Er=Rands ∑2Kr(rij−rij′)2
键角
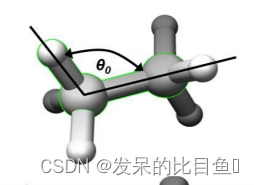
E
θ
=
∑
angles
K
θ
2
(
θ
i
j
−
θ
i
j
′
)
2
E_\theta=\sum_{\text {angles }} \frac{K_\theta}{2}\left(\theta_{i j}-\theta_{i j}^{\prime}\right)^2
Eθ=angles ∑2Kθ(θij−θij′)2
二面角

E
χ
=
∑
dihedrals
V
n
2
[
1
+
cos
(
n
χ
i
j
k
l
−
δ
)
]
E_\chi=\sum_{\text {dihedrals }} \frac{V_n}{2}\left[1+\cos \left(n \chi_{i j k l}-\delta\right)\right]
Eχ=dihedrals ∑2Vn[1+cos(nχijkl−δ)]
非键价能
非键价能,一般用两部分来描述:其一为静电相互作用能,通过库伦定律来计算;后者为范德华相互作用,采用Lennard-Jones势能函数来描述。
∑
nonbij
(
A
i
j
r
i
j
12
)
−
(
B
i
j
r
i
j
6
)
A
i
j
=
ε
i
ε
j
(
R
i
+
R
j
2
)
12
B
i
j
=
2
ε
i
ε
j
(
R
i
+
R
j
2
)
6
\begin{aligned} & \sum_{\text {nonbij }}\left(\frac{A_{i j}}{r_{i j}^{12}}\right)-\left(\frac{B_{i j}}{r_{i j}^6}\right) \\ & A_{i j}=\sqrt{\varepsilon_i \varepsilon_j}\left(\frac{R_i+R_j}{2}\right)^{12} \\ & B_{i j}=2 \sqrt{\varepsilon_i \varepsilon_j}\left(\frac{R_i+R_j}{2}\right)^6 \end{aligned}
nonbij ∑(rij12Aij)−(rij6Bij)Aij=εiεj(2Ri+Rj)12Bij=2εiεj(2Ri+Rj)6
范德华力
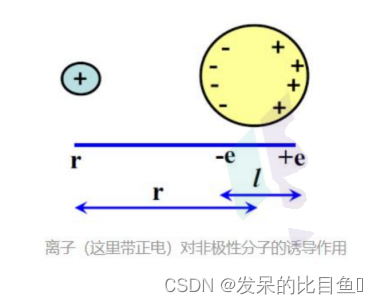
范德华力(英语:van der Waals’Forces;又名:范德瓦耳斯力)在化学中指分子或非极性原子(稀有气体)之间非定向的、无饱和性的、较弱的相互作用力,包括排斥力和吸引力。根据荷兰物理学家van der Waals(约翰内斯·范德瓦耳斯)命名,其于1910获得Noble物理奖。范德华力是分别来自两个分子中的一种中性原子之间通过瞬间静电相互作用产生的一种弱的分子之间的力,这是由于附近粒子波动极化的相关性引起的(量子动力学的结构),具体而言,电子密度可能会暂时更大地转移到原子核的一侧。这会产生一个瞬态电荷,附近的原子可以被吸引或排斥。但它比化学键或共价键弱得多,通常其能量小于5kJ/mol(O.4~4kJ/mol)。当两个原子之间的距离为它们的范德华半径之和时,范德华引力最强。强的范德华排斥作用可以防止原子相互靠近。范德华力的大小和分子的大小成正比。
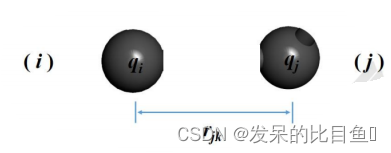
E ( r ) = 1 4 π ε 0 q i q j ε r E(r)=\frac{1}{4 \pi \varepsilon_0} \frac{q_i q_j}{\varepsilon r} E(r)=4πε01εrqiqj
非键价能(静电相互作用能,范德华相互作用)只在两种情况下计算
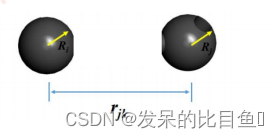
两原子分属于两个分子
两个原子属于同一个分子但其
间隔多于两个连接的化学键
力场历史
- ff84(parm91X.ua.dat)
最早的AMBER力场,用于模拟核酸和蛋白质的联合原子力场。 - ff86力场(parm91X.dat)。
将f84扩展为全原子力场。和f84一样对氢键也是用Lennard-Jones 10-12势。 - ff94力场(parm94.dat)
来自Cornell.Kollman et al。适合溶剂环境。电荷由RESPHF/6-31G*获得。 - f96力场(parm96.dat)
来自Beachy et al,算出来的能量更接近量化结果,但构象有明显偏向beta等问题。 - ff99力场(parm99.dat)
大部分参数来自94力场,修改了许多扭转角的参数。甘氨酸的骨架参数有问题,螺旋和延展构象的平衡性不对 - ff02力场(parm99.dat+frcmod.ff02pol.rl)
999力场的可极化版,增加了可极化的偶极子 - ff03(parm99.dat+frcmod.ff03)
来自Yong Duan etal.获取电荷时通过连续介电模型表现溶剂可极化效应,修改了蛋白phi、psi骨架参数,减少了对螺旋构象的偏爱。 - fl0力场(parm10.dat)
对f99的各种参数补丁的集合,相当于parm99.dat+frcmod.ff03+bsc0+chi.OL3+
新的离子参数+原子和残基名的修改以顺应PDB format version3。 - ff12SB(parm10.dat+frcmod.ff12SB)
对骨架及侧链的扭转参数进行修正,。 - ff14SB(parm10.dat+frcmod.ff14SB)
继续对骨架及侧链的扭转参数进行修正,并对二面角进行修正ff19力场(parm19.dat+frcmod.ff19SB)
改善蛋白质结构依赖性,例如螺旋倾向,并再现了氨基酸特异性拉氏图差异
力场选择推荐
| Moleculel/on Type | Force Field |
|---|---|
| protein | ff19SB |
| DNA | OL15 |
| RNA | OL3 |
| carbohydrates | GLYCAM_06j |
| lipids | lipids 17 |
| organic molecules(usually ligands) | gaff2 |
| ions | should be matched to water model;see force fields for ions for further discussion |
| water model | should be matched to atomic ions; common water models include tip3p, spc/e,tip4pew,and OPC |
能量最小化
能量极小化算法
-
一级微商算法
- 最陡下降算法Steepest Descents-SD
- 共轮梯度算法Conjugate Gradients-CONJ
-
二级微商算法
- Newton-Raphson Method
-
能量极小化算法比较
- 最陡下降法:
- 方向变化大,收敛慢,优化辐度大。
- 共辄梯度法
- 收敛快,易陷入局部势阱,对初始结构偏离不大。
- Newton-Raphson法
- 计算量较大,当微商小时收敛快。
- 最陡下降法:
由于我们进行的初始结构来自晶体结构或同源建模,所以在分子内部存在着一定的结构张力,可能会存在两个原子靠得太近的情况(称之为bad contact),能量最小化就是真正的动力学之前释放这些张力,如果没有这个步骤,在动力学模拟开始之后,整个体系可能会因此变形、散架。所以需要在正式模拟开始的第一步对体系进行能量最小化
比较常用的能量最小化方法有两种,最速下降法和共扼梯度法.最速下降法是快速移除体系内应力的好方法,但是接近能量极小点时收敛比较慢,而共梯度法在能量极小点附近收敛效率高一些.所以一般做能量最小化时都是先利用最速下降法进行优化,完成之后再对得到的构象利用共梯度法优化一次,这样做能有效地保证后续模拟的进行.
注意:
1、由于只是局部优化,这样的计算只能找到所用的初始构象附近的“最优构象”。所以选择初始构象是非常关键的。
2、若为找到全局能量最低构象,须将所有可能的初始构象分别进行优化,最后进行比较,确定分子体系的最优构象。
3、对于较大的分子,可能的初始构象的数目会随原子数目的增加而急剧增加。在选择初始构象时,应把从基本的化学知识方面考虑是不可能的构象略去。
溶剂化模型

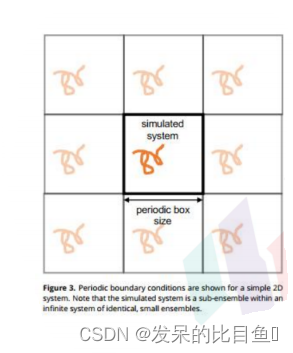
该模型直接将研究体系放在水盒子中,通常还添加抗衡离子以中和体系电荷。这种直接模拟溶质与溶剂之间相互作用的方法,大大提高了模拟的准确性,但大量水分子也会带来计算量的急剧增加。通常使用一定大小的水盒子把溶质包裹起来,采用周期边界条件(periodic boundary condition,PBC)
来表现无限溶剂环境。
隐式溶剂模型: 模仿的溶剂特性而没有真实的溶剂分子
该模型不添加水分子,而用连续介质模型(数学方程)来反映该效应。隐式溶剂模型有许多优势,包括:减少体系粒子数目,降低计算开销;无溶剂摩擦效应,加快构像变化,避免长时间模拟;无需显式水的平衡过程。最著名的模型为广义波恩(Generalized Born, GB)方法。
通常,我们在做常规分子动力学模拟时会采用显式溶剂模型,而在之后的结合自由能计算则采用隐式溶剂模型(MM/GB(PB)SA方法)。
周期边界条件
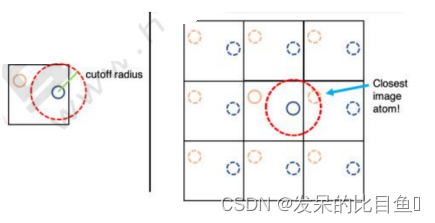
范德华公式
(
A
i
j
r
i
j
12
)
−
(
B
i
j
r
i
j
6
)
\text { 范德华公式 } \quad\left(\frac{A_{i j}}{r_{i j}^{12}}\right)-\left(\frac{B_{i j}}{r_{i j}^6}\right)
范德华公式 (rij12Aij)−(rij6Bij)
计算单元格中蓝色原子和黄色原子的范德华势能,首先要计算两个原子之间的距离考虑到截断半径,一般是单元格长度的一半
计算的范德华势能其实是蓝色原子和镜像中的黄色原子
能量优化
体系的优化分为两步,第一步固定蛋白和小分子,对添加的水盒优化。第二步则是对整个体系的优化。
vim min1.in
min with restrain
&cntr1
imin}=1,
maxcyc =10000,
ncyc}=5000,
ntb =1,
ntr =1,
ntpr =500,
cut =10,
ioutfm =1,
ntxo =1,
restraint_wt =500.0,
restraintmask = ' :1-199',
/
vim min2.in
min with no-restrain
&cntrl
imin =1,
maxcyc =50000,
ncyc =25000,
ntb =1,
ntr =0,
cut =10,
ntpr =500,
ioutfm =1,
ntxo=1,
/
imin
=
1
单点能量计算,做到最小化
\operatorname{imin}=1 \quad \text { 单点能量计算,做到最小化 }
imin=1 单点能量计算,做到最小化
n
t
p
r
=
1
这个表明采集计算信息的频率, 输出到 mdout 文件中。
ntpr=1 \quad \text { 这个表明采集计算信息的频率, 输出到 mdout 文件中。}
ntpr=1 这个表明采集计算信息的频率, 输出到 mdout 文件中。
n
t
b
=
1
采用周期性边界的恒容条件
,
表明这是一
N
V
T
系综
,
周期性边界在附录中说明
ntb=1 采用周期性边界的恒容条件, 表明这是一 NVT 系综, 周期性边界在附录中说明
ntb=1采用周期性边界的恒容条件,表明这是一NVT系综,周期性边界在附录中说明
c
u
t
=
9.0
由于计算能量时需要有一个截断距离, 这个参数指定截断距离。
cut=9.0 \text { 由于计算能量时需要有一个截断距离, 这个参数指定截断距离。 }
cut=9.0 由于计算能量时需要有一个截断距离, 这个参数指定截断距离。
n
t
r
=
1
增加限制力
,
与下面的
H
o
l
d
t
h
e
p
r
o
t
e
i
n
f
i
x
e
d
照应或者出现
r
e
s
t
r
a
i
n
t
_
w
t
标识
ntr=1 增加限制力, 与下面的 Hold \quad the \quad protein \quad fixed 照应或者出现 restraint\_wt 标识
ntr=1增加限制力,与下面的Holdtheproteinfixed照应或者出现restraint_wt标识
maxcyc
=
5000
能量最小化的算法涉及循环迭代, 这里指定迭代次数。
\operatorname{maxcyc}=5000 \text { 能量最小化的算法涉及循环迭代, 这里指定迭代次数。 }
maxcyc=5000 能量最小化的算法涉及循环迭代, 这里指定迭代次数。
n
t
m
i
n
=
1
最小化方法的标志
,
n
t
m
i
n
=
1
表示先用最陡下降法优化, 然后用共轪梯度法
ntmin =1 最小化方法的标志, ntmin=1 \text { 表示先用最陡下降法优化, 然后用共轪梯度法 }
ntmin=1最小化方法的标志,ntmin=1 表示先用最陡下降法优化, 然后用共轪梯度法
n
c
y
c
=
2500
ncyc=2500
ncyc=2500 如上所说, 循环迭代的算法不同, 此处指定到哪一步第一种迭代算法结束。表示先用 2500 步的最陡下降法优化然后做 2500 步共轭梯度法优化
升高温度
由于动力学模拟的是真实的生物体环境,因此必须使研究对象升温升压到临界值,体系达到平衡,才能做实际的动力学模拟
hot to 300k
imin =0,
irest =0,
ntx =1,
ntb =1,
cut =10,
ntr =1,
ntc =2,
ntf =2,
tempi =0.0,
tempo =300.0,
ntt =3,
gamma_ln =1.0,
nstlim =150000,
dt =0.002,
ntpr =500,
ntwx =1000,
ntwr =500,
restraint_wt =10.0,
restraintmask ='1: 1-199',
imin
=
0
\operatorname{imin}=0 \quad
imin=0 开始做动力学, 而不是能量最小化。
n
m
r
o
p
t
=
1
nmropt=1
nmropt=1 这个参数原本用于指定
n
m
r
\mathrm{nmr}
nmr 限制, 现在被机智地借来用于控制升温过程。
n
t
w
r
=
500
ntwr=500
ntwr=500 采集计算信息的频率, 每隔 100 步打印一次信息写入 restrt 文件中
n
t
f
=
2
\mathrm{ntf}=2
ntf=2 忽略涉及到
H
\mathrm{H}
H 原子的键的相互作用
n
s
t
l
i
m
=
25000
nstlim=25000
nstlim=25000 动力学过程的步长, 前面说过动力学的原理, 它是连续地解牛顿运动方程。动力学的时长会等于步长 (nstlim) 乘以每一步的时间间隔(如下,
d
t
)
\mathrm{dt})
dt) 。
d
t
=
0.002
\mathrm{dt}=0.002
dt=0.002 每一步的时间间隔,单位是 ps。
n
t
p
=
0
\mathrm{ntp}=0 \quad
ntp=0 暂时不考虑控制压力
n
t
t
=
3
ntt=3
ntt=3用郎之万动力学的方法, 且需要设置一个 gamma_ln 值。
gamma_
ln
=
2.0
\ln =2.0
ln=2.0 以上两个参数指定如何控制温度。
n
t
c
=
2
\mathrm{ntc}=2
ntc=2 以上两个参数针对氢原子做 shake 限制, 主要由于氢原子的振动频率过高, 氢原子的
运动还存在量子效应。所以涉及到
H
\mathrm{H}
H 原子的键需要被限制
t
e
m
p
i
=
0.0
tempi=0.0
tempi=0.0 初始的模拟温度, 单位为
K
\mathrm{K}
K
t
e
m
p
0
=
300.0
temp0=300.0
temp0=300.0升温后的温度, 单位为
K
\mathrm{K}
K
t
o
l
=
0.000001
tol=0.000001
tol=0.000001 用 shake 重新设置坐标的一个几何公差
注意:
irest
=
1
,
n
t
x
=
5
irest
=
0
,
n
t
x
=
1
\begin{aligned} & \text { irest }=1, n t x=5 \\ & \text { irest }=0, n t x=1 \end{aligned}
irest =1,ntx=5 irest =0,ntx=1
动力学模拟
一般来说第一步的MD模拟时间要长一些, 确保体系构象已 经稳定, 之后进行第二步的MD用于能量、相互作用分析等。
md for 40 ns
&cntrl
imin =0,
irest =1,
ntx =7,
ntb =2,
pres0=1.0,
ntp =1,
taup =2.0,
cut =10,
ntr=0,
ntc=2,
ntf =2,
tempi =300.0,
temp0=300.0,
ntt =3,
gamma_ln =1.0,
nstlim =20000000,
dt=0.002,
ntpr =500,
ntwx =500,
ntwr =500
/
&cntrl
imin =0,
irest =1,
ntx =7,
ntb =2,
pres0=1.0,
ntp =1,
taup =2.0,
cut=10,
ntr =0,
ntc=2,
ntf=2,
tempi =300.0,
temp0=300.0,
ntt=3, gamma_ln =1.0,
nstlim =5000000, dt=0.002,
ntpr =500, ntwx =500, ntwr =500,
ntwprt =3204,
/
n
t
x
=
5
n t x=5 \quad
ntx=5 Read coordinates and velocities from unformatted inpcrd coordinate file
n
t
x
n t x
ntx 等于 5 表示将读取另一种格式的 inpcrd 文件, 它往往配合 irest=1 (如下) 使用。
irest
=
1
=1
=1 Restart previous MD run [This means velocities are expected in the inpcrd file and will be
used to provide initial atom velocities]
irest 等于 1 表明将重启上一次的动力学, 也就意味着希望能从输入文件中读取到上
一次动力学结束时对应的 (除了坐标信息外的) 原子速度信息 (储存在 rst 文件中)。
t
e
m
p
0
=
300.0
temp0=300.0
temp0=300.0 Thermostat temperature. Run at
300
K
300 \mathrm{~K}
300 K
动力学过程中需要控制保持的温度,一般在
300
K
300 \mathrm{~K}
300 K 左右
n
t
b
=
2
ntb=2 \quad
ntb=2 Use periodic boundary conditions with constant pressure
采用周期性边界的恒压条件。一般动力学即采用此 NPT 系综。
n
t
p
=
1
ntp=1 \quad
ntp=1 Use the Berendsen barostat for constant pressure simulation
设定控压的算法。
i
g
=
−
1
ig =-1
ig=−1 The seed for the pseudo-random number generator, If
i
g
=
−
1
i g=-1
ig=−1, the random seed willbe based on the current date and time, and hence will be different for every run
n
t
r
=
1
ntr=1
ntr=1 Flag for restraining specified atoms in Cartesian space using a harmonic potential, if
n
t
r
>
0
n t r>0
ntr>0.
The restrained atoms are determined by the restraintmask string