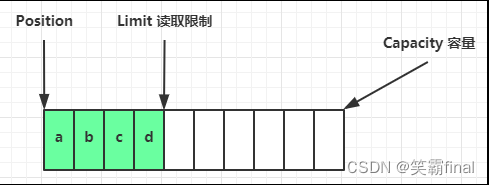
首先看
汉明码
一、矩阵解释 单bit纠正( SEC,single error correction )
以数据位为8位(m)为例,编码位数为r,2^r>=m+r+1
r最小为4
编码后位数为4+8=12位
编码位为p1,p2 ,p3, p4
p1掌控:d1 d2 d4 d5 d7,分别对应位置是:11,101,111,1001,1011(也就是位置的二进制编码,第一位为1的,注意p1由其掌控的数据为求取得到)
p2掌控:d1 d3 d4 d6 d7,分别对应位置是: 11,110,111,1010,1011(也就是位置的二进制编码,第二位为1的)
p3:... :d2 d3 d4 d8(第三位为1的)
p4:....: d5 d6 d7 d8(第四位为1的)
|
位置编码
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
9
|
10
|
11
|
12
|
13
|
14
|
|
位置二进制编码
|
1
|
10
|
11
|
100
|
101
|
110
|
111
|
1000
|
1001
|
1010
|
1011
|
1100
| ||
|
数据为和编码为标志
|
p1
|
p2
|
d1
|
p3
|
d2
|
d3
|
d4
|
p4
|
d5
|
d6
|
d7
|
d8
| ||
|
p1
|
1
|
1
|
1
|
1
|
1
|
1
| ||||||||
|
p2
|
1
|
1
|
1
|
1
|
1
|
1
| ||||||||
|
p3
|
1
|
1
|
1
|
1
|
1
| |||||||||
|
p4
|
1
|
1
|
1
|
1
|
1
|
根据上表可以得到奇偶校验矩阵H:
H=
1 0 1 0 1 0 1 0 1 0 1 0
0 1 1 0 0 1 1 0 0 1 1 0
0 0 0 1 1 1 1 0 0 0 0 1
0 0 0 0 0 0 0 1 1 1 1 1
比如数据为1001_1100, 按照奇校验求取得到下表(就是保证所有位(包括校验位p)的1的个数是奇数)。
p1=^(10110)+1= 0(因为是奇数所以p1=0,这里1+1不进位,所以等于0)
p2=^(10110) +1 = 0
p3=^(00010)+1 = 0
p4=^(1100)+1=1 (因为是偶数所以p4=1)
|
位置编码
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
9
|
10
|
11
|
12
|
13
|
14
|
|
位置二进制编码
|
1
|
10
|
11
|
100
|
101
|
110
|
111
|
1000
|
1001
|
1010
|
1011
|
1100
| ||
|
数据为和编码为标志
|
p1
|
p2
|
d1
|
p3
|
d2
|
d3
|
d4
|
p4
|
d5
|
d6
|
d7
|
d8
| ||
|
值
|
0
|
0
|
1
|
0
|
0
|
0
|
1
|
1
|
1
|
1
|
0
|
0
| ||
|
p1
|
1
|
1
|
1
|
1
|
1
|
1
| ||||||||
|
p2
|
1
|
1
|
1
|
1
|
1
|
1
| ||||||||
|
p3
|
1
|
1
|
1
|
1
|
1
| |||||||||
|
p4
|
1
|
1
|
1
|
1
|
1
|
编码后数据流是:0 0 1 0 0 0 1 1 1 1 0 0
如果对方接受到的数据是0 0 1 0 0 0 1 1 1 1 0 0那么数据流和奇偶校验矩阵的乘积 矩阵
相乘并模2加法应该是一个全1矩阵,表示没有位置出错。
理解:
实际上就是对p和p所掌控的数据位重新取异或。(因为编码使,p和p所掌控的数据是按照奇校验计算的,所以对这些位重新取异或后值应该为1)
模二加法的话是1+1=0,1+0=1不进位
数据流是:
0 0 1 0 0 0 1 1 1 1 0 0
乘法:
1 0 1 0 1 0 1 0 1 0 1 0 0 1
0 1 1 0 0 1 1 0 0 1 1 0 * 0 1
0 0 0 1 1 1 1 0 0 0 0 1 1 = 1
0 0 0 0 0 0 0 1 1 1 1 1 0 1
0
0
1
1
1
1
0
0
A、如果接收到的单bit出错,比如第5位(d2):0 0 1 0 1 0 1 1 1 1 0 0
数据流是:
0 0 1 0 1 0 1 1 1 1 0 0
矩阵乘法:
1 0 1 0 1 0 1 0 1 0 1 0 0 0 p1'
0 1 1 0 0 1 1 0 0 1 1 0 * 0 1 p2'
0 0 0 1 1 1 1 0 0 0 0 1 1 = 0 p3'
0 0 0 0 0 0 0 1 1 1 1 1 0 1 p4'
1
0
1
1
1
1
0
0
计算出来结果不是全1的,所以存在错误,如果是单bit出错,计算结果0101=5就表示出错位置,但是高于1bit的话实际上也会爆出来是出错,只是没有办法确认是哪几位。
p1'和p3'与值为0说明奇校验没有过。
图解释,如下,d2出错,从图中可以很形象的确认出p1'和p3'会报错:
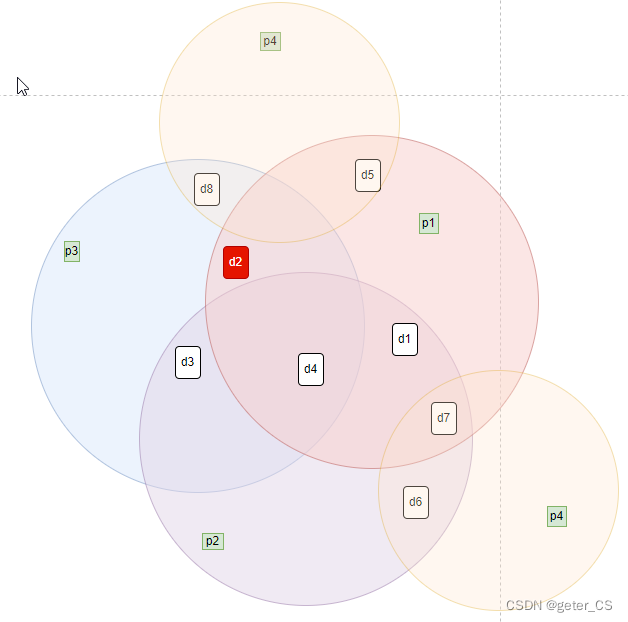
B、如果接收到的两bit出现错误
原始编码后数据: 0 0 1 0 0 0 1 1 1 1 0 0
如果第5位(d2)和第11位(d7)位出错:0 0 1 0 1 0 1 1 1 1 1 0
数据流是:
0 0 1 0 1 0 1 1 1 1 1 0
矩阵乘法:
1 0 1 0 1 0 1 0 1 0 1 0 0 1 p1'
0 1 1 0 0 1 1 0 0 1 1 0 * 0 0 p2'
0 0 0 1 1 1 1 0 0 0 0 1 1 = 0 p3'
0 0 0 0 0 0 0 1 1 1 1 1 0 0 p4'
1
0
1
1
1
1
1
0
从计算结果来看p2',p3',p4'计算出来有错误,奇校验没有过,但是p1'是正确的。1000=8没法确认出错的bit。
如下图所示,因为d2和d7都在p1中所以,求异或后抵消了,所以p1'是计算出来正确的。由于d2出错,所以p3'报错,由于d7出错,所以p4'和p2'报错。从图上也知道没法确认出错bit,也没有办法确认出错bit数量。也没法纠正。
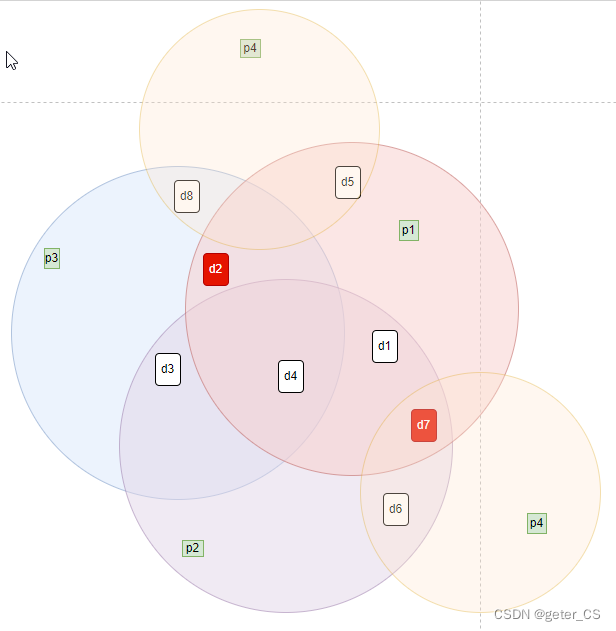
二、矩阵解释 单bit纠正,两bit检测( SECDED,single error correction and double error detection)(3bit err not work)
实现这种校验,需要额外增加一个校验位
global parity check bit,称为g
依然按照上面两种情况举例。
|
位置编码
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
9
|
10
|
11
|
12
|
13
|
14
|
|
位置二进制编码
|
1
|
10
|
11
|
100
|
101
|
110
|
111
|
1000
|
1001
|
1010
|
1011
|
1100
| ||
|
数据为和编码为标志
|
p1
|
p2
|
d1
|
p3
|
d2
|
d3
|
d4
|
p4
|
d5
|
d6
|
d7
|
d8
|
g
| |
|
值
|
0
|
0
|
1
|
0
|
0
|
0
|
1
|
1
|
1
|
1
|
0
|
0
|
0
| |
|
p1
|
1
|
1
|
1
|
1
|
1
|
1
| ||||||||
|
p2
|
1
|
1
|
1
|
1
|
1
|
1
| ||||||||
|
p3
|
1
|
1
|
1
|
1
|
1
| |||||||||
|
p4
|
1
|
1
|
1
|
1
|
1
| |||||||||
|
g
|
1
|
1
|
1
|
1
|
1
|
1
|
1
|
1
|
1
|
1
|
1
|
1
|
g的话是所有为校验位:^(0 0 1 0 0 0 1 1 1 1 0 0)+1=0
编码后数据流是: 0 0 1 0 0 0 1 1 1 1 0 0 0
A、如果接收到的单bit出错,比如第5位(d2):0 0 1 0 1 0 1 1 1 1 0 0 0
数据流是:
0 0 1 0 1 0 1 1 1 1 0 0 0
矩阵乘法:
1 0 1 0 1 0 1 0 1 0 1 0 0 0 0 p1'
0 1 1 0 0 1 1 0 0 1 1 0 0 * 0 1 p2'
0 0 0 1 1 1 1 0 0 0 0 1 0 1 = 0 p3'
0 0 0 0 0 0 0 1 1 1 1 1 0 0 1 p4'
1 1 1 1 1 1 1 1 1 1 1 1 1 1 0 g'
0
1
1
1
1
0
0
0
计算出来结果不是全1的,所以存在错误,如果是单bit出错(注意这里用的如果),计算结果0101=5就表示出错位置。由于g'不等于1所以整体上来说奇偶校验没有过存在错误的bit。
而且p1'和p3'也出错了。如果是单bit出错所以是可以找到对应bit并纠正的。(注意这里是如果)
整体出错,分量也出错,那么是单bit出错(
前提是没有超过3bit出错)
图解释,如下,d2出错,从图中可以很形象的确认出p1'和p3'会报错,g也会报错:
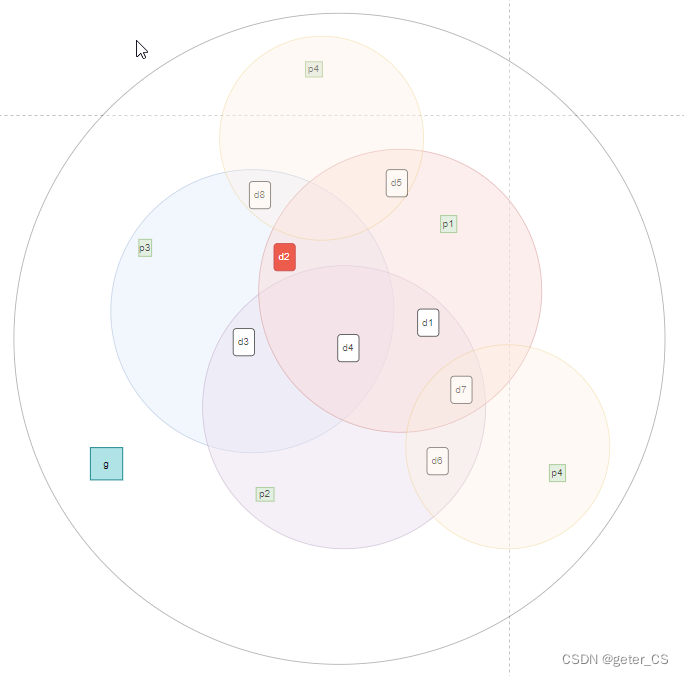
B、如果接收到的两bit出现错误
原始编码后数据: 0 0 1 0 0 0 1 1 1 1 0 0 0
如果第5位(d2)和第11位(d7)位出错:0 0 1 0 1 0 1 1 1 1 1 0 0
数据流是:
0 0 1 0 1 0 1 1 1 1 1 0 0
矩阵乘法:
1 0 1 0 1 0 1 0 1 0 1 0 0 0 1 p1'
0 1 1 0 0 1 1 0 0 1 1 0 0 * 0 0 p2'
0 0 0 1 1 1 1 0 0 0 0 1 0 1 = 0 p3'
0 0 0 0 0 0 0 1 1 1 1 1 0 0 0 p4'
1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 g'
0
1
1
1
1
1
0
从计算结果来看p2',p3',p4'计算出来有错误,但是p1’和g'是正确的。1000=8没法确认出错的bit。
如下图所示,因为d2和d7都在p1中所以,求异或后抵消了,所以p1'是计算出来正确的(g'也是一样的)。由于d2出错,所以p3'报错,由于d7出错,所以p4'和p2'报错。从图上也知道没法确认出错bit,也没法纠正。由于
整体是正确的,但是分量有错误,所以判断出事两个bit出错了,但是没法纠正也没法确认出错bit。(
前提是没有超过3bit出错)

C.如果接收到的是3 bits错误或以上,SECDED没法work。
原始编码后数据: 0 0 1 0 0 0 1 1 1 1 0 0 0
如果第5位(d2)和第11位(d7)以及第10位(d6)出错:0 0 1 0 1 0 1 1 1 0 1 0 0
数据流是:
0 0 1 0 1 0 1 1 1 0 1 0 0
矩阵乘法:
1 0 1 0 1 0 1 0 1 0 1 0 0 0 1 p1'
0 1 1 0 0 1 1 0 0 1 1 0 0 * 0 1 p2'
0 0 0 1 1 1 1 0 0 0 0 1 0 1 = 0 p3'
0 0 0 0 0 0 0 1 1 1 1 1 0 0 1 p4'
1 1 1 1 1 1 1 1 1 1 1 1 1 1 0 g'
0
1
1
1
1
1
0
从计算结果来看p3'计算出来有错误,但是p1’,p2’,p4'和g'是正确的。1101=13没法确认出错的bit。
如下图所示,因为d2和d7都在p1中所以,求异或后抵消了,所以p1'是计算出来正确的。由于d2出错,所以p3'报错,由于d7和d6出错,所以p4'和p2'校验正确。
由于有三个bit错误没法抵消,所以g'也是奇校验没有通过。
由于整体是错误的,分量也有错误,从下图也知道没法确认出错bit数,也没法纠正。
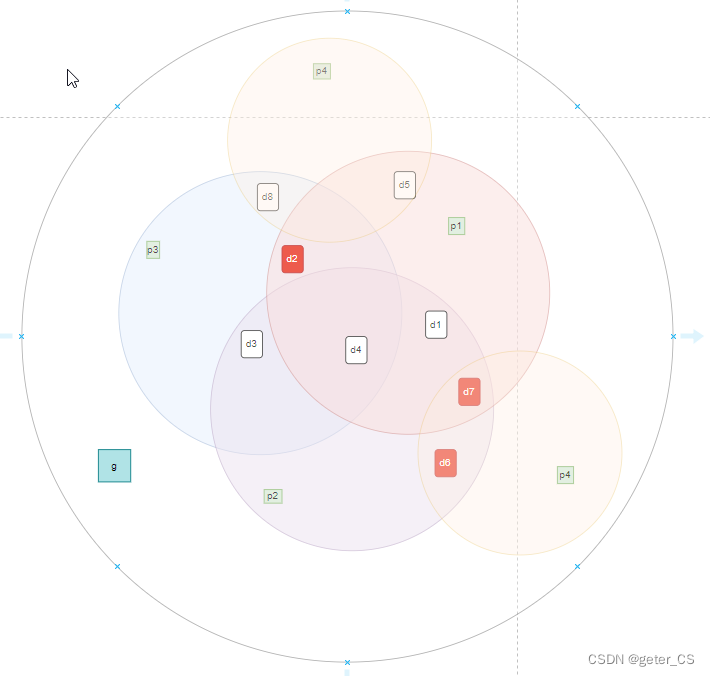
所以超过三个bits出错的话没法work。超过3个bit(包括三个)没法区分是哪个bit出错,出错了几个bit。但是能分出是奇数个还是偶数个。
整体校验通过,分量没有通过那么是偶数个bit出错。
整体校验失败,分量校验也失败的话那么是奇数个bit出错。
从上面分析可以得出另一个结论是,实际上划分p1,p2,p3,p4所掌控的数据,并不一定要按照上面的规则去划分,按照图像解释只要能保证单个bit出错能定位到该bit就可以。
也就是校验矩阵可以采用其
三.生成码和校验码(G and
H
)
A.校验矩阵
|
位置编码
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
9
|
10
|
11
|
12
|
13
|
14
|
|
位置二进制编码
|
1
|
10
|
11
|
100
|
101
|
110
|
111
|
1000
|
1001
|
1010
|
1011
|
1100
| ||
|
数据为和编码为标志
|
p1
|
p2
|
d1
|
p3
|
d2
|
d3
|
d4
|
p4
|
d5
|
d6
|
d7
|
d8
| ||
|
值
|
0
|
0
|
1
|
0
|
0
|
0
|
1
|
1
|
1
|
1
|
0
|
0
| ||
|
p1
|
1
|
1
|
1
|
1
|
1
|
1
| ||||||||
|
p2
|
1
|
1
|
1
|
1
|
1
|
1
| ||||||||
|
p3
|
1
|
1
|
1
|
1
|
1
| |||||||||
|
p4
|
1
|
1
|
1
|
1
|
1
|
实际上校验码矩阵H中,是可以将p和d位置分开来的。
原来的校验矩阵H是上表中的红色以及框起来的部分组成的,形式如下
1 0 1 0 1 0 1 0 1 0 1 0
0 1 1 0 0 1 1 0 0 1 1 0
0 0 0 1 1 1 1 0 0 0 0 1
0 0 0 0 0 0 0 1 1 1 1 1
如果将数据和校验位分开不做穿插排列的话(原始数据还是1001_1100),可排成如下表格:
|
位置编码
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
9
|
10
|
11
|
12
|
13
|
14
|
|
位置二进制编码
|
1
|
10
|
100
|
1000
|
101
|
110
|
111
|
1001
|
1010
|
1011
|
1100
|
1101
| ||
|
数据为和编码为标志
|
p1
|
p2
|
p3
|
p4
|
d1
|
d2
|
d3
|
d4
|
d5
|
d6
|
d7
|
d8
| ||
|
值
|
0
|
0
|
0
|
1
|
1
|
0
|
0
|
1
|
1
|
1
|
0
|
0
| ||
|
p1(位置编号第一位为1的数据)
|
1
|
1
|
1
|
1
|
1
|
1
| ||||||||
|
p2(位置编号第二位为1的数据)
|
1
|
1
|
1
|
1
|
1
| |||||||||
|
p3(位置编号第三位为1的数据)
|
1
|
1
|
1
|
1
|
1
|
1
| ||||||||
|
p4(位置编号第4位为1的数据)
|
1
|
1
|
1
|
1
|
1
|
1
|
(注意表格中:位置二进制编码也往前提了)
那么现在的校验矩阵H就是两部分组成,一部分是校验位的单位阵(eye,上表黄色框部分),一部分是数据位的归属阵(上表红色框部分):
p1 p2 p3 p4 d1 d2 d3 d4 d5 d6 d7 d8
1 0 0 0 1 0 1 1 0 1 0 1
0 1 0 0 0 1 1 0 1 1 0 0
0 0 1 0 1 1 1 0 0 0 1 1
0 0 0 1 0 0 0 1 1 1 1 1 (4*12)
生成矩阵G也是有两部分组成,一个是数据位归属阵的转置阵( 行换成同序数的列),一部分是数据的单位阵(eye):
p1 p2 p3 p4 d1 d2 d3 d4 d5 d6 d7 d8
1 0 1 0 1 0 0 0 0 0 0 0
0 1 1 0 0 1 0 0 0 0 0 0
1 1 1 0 0 0 1 0 0 0 0 0
1 0 0 1 0 0 0 1 0 0 0 0
0 1 0 1 0 0 0 0 1 0 0 0
1 1 0 1 0 0 0 0 0 1 0 0
0 0 1 1 0 0 0 0 0 0 1 0
1 0 1 1 0 0 0 0 0 0 0 1 (8*12)
B.生成矩阵
生成矩阵G可以用于在编码器中生成编码后打代码。
公式是c=
mG
比如上面源码m是
1001_1100,矩阵乘法后,取模二加法再+1(奇校验):
mG=
1 0 0 1 1 1 0 0 (1*8)*
1 1 0 1 0 1 0 0 0 0 0 0 0
0 0 1 1 0 0 1 0 0 0 0 0 0
0 1 1 1 0 0 0 1 0 0 0 0 0
1 1 0 0 1 0 0 0 1 0 0 0 0
1 0 1 0 1 0 0 0 0 1 0 0 0
1 1 1 0 1 0 0 0 0 0 1 0 0
0 0 0 1 1 0 0 0 0 0 0 1 0
0 1 0 1 1 0 0 0 0 0 0 0 1 (8*12)= 0 1 0 0 1 0 0 1 1 1 0 0(1*12)
(方便看着计算例了这列) p1 p2 p3 p4 d1 d2 d3 d4 d5 d6 d7 d8
最终求出的矩阵(1*12)就是编码后的数据,前四位是校验位,后面8位是原数据没变。
p1=^(d1d3d5d7)+1=^(1010)+1=1
p2=^(d2d3d6d7)+1=^(0010)+1=0
C.校验
奇校验情况下如果收到的码是正确的,那么可H和收到的数据相乘应该为全为一(取模二加法):
接收到的正确的码:
0 1 0 0 1 0 0 1 1 1 0 0
校验:
1 0 0 0 1 0 1 1 0 1 0 1
0 1 0 0 0 1 1 0 1 1 0 0 *
0 0 1 0 1 1 1 0 0 0 1 1
0 0 0 1 0 0 0 1 1 1 1 1 (4*12)
0
1
0
0
1 1
0 = 1
0 1
1 1
1
1
0
0(12*1)
只要生成矩阵和校验矩阵能够对应上,就能进行编码和校验,并不一定说要p1使用第一位为1的位置,p2使用第二位为1的位置。
(我也可以p1使用第一位为0,p2第二位为0的位置)
四.任意生成矩阵和校验矩阵(不完全正确自己理解的总结)
三中例子,4位的矫正位,可以表示16个错误位。(还是奇校验),可以写成如下错码表
|
位置编码
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
9
|
10
|
11
|
12
|
13
|
14
|
|
位置二进制编码
|
1
|
10
|
100
|
1000
|
101
|
110
|
111
|
1001
|
1010
|
1011
|
1100
|
1101
| ||
|
错码位
|
p1
|
p2
|
p3
|
p4
|
d1
|
d2
|
d3
|
d4
|
d5
|
d6
|
d7
|
d8
| ||
|
p1'p2'p3'p4'
|
0111
|
1011
|
1101
|
1110
|
0101
|
1001
|
0001
|
0110
|
1010
|
0010
|
1100
|
0100
|
图像解释:
0111表示p1'计算出来不正确,所以错误位是p1 (表示p1属于p1)
1001表示p2'p3'计算出来不正确,所以错误位是d2(1001表示d2属于p2和p3)
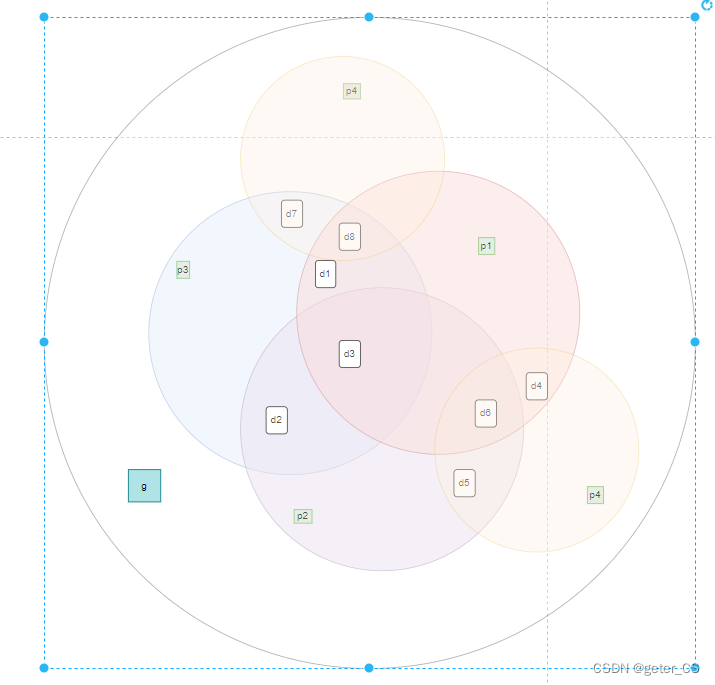
从这个错码表可以知道,实际上可以通过错码表来生成校验和生成矩阵,而且错码表示可以任意的,只需要保证每一个错码表示唯一一个可能的错位。这样就可以在只有一个bit出错时可以纠正。
五.代码
编码器这个编码器使用的是SECDED,且也不是按照 p
1使用第一位为1的位置,p2使用第二位为1的位置来计算的,可能使用错码表思路。

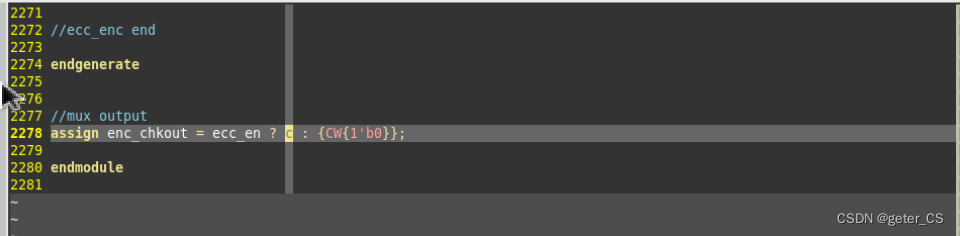
解码器,并进行纠正。
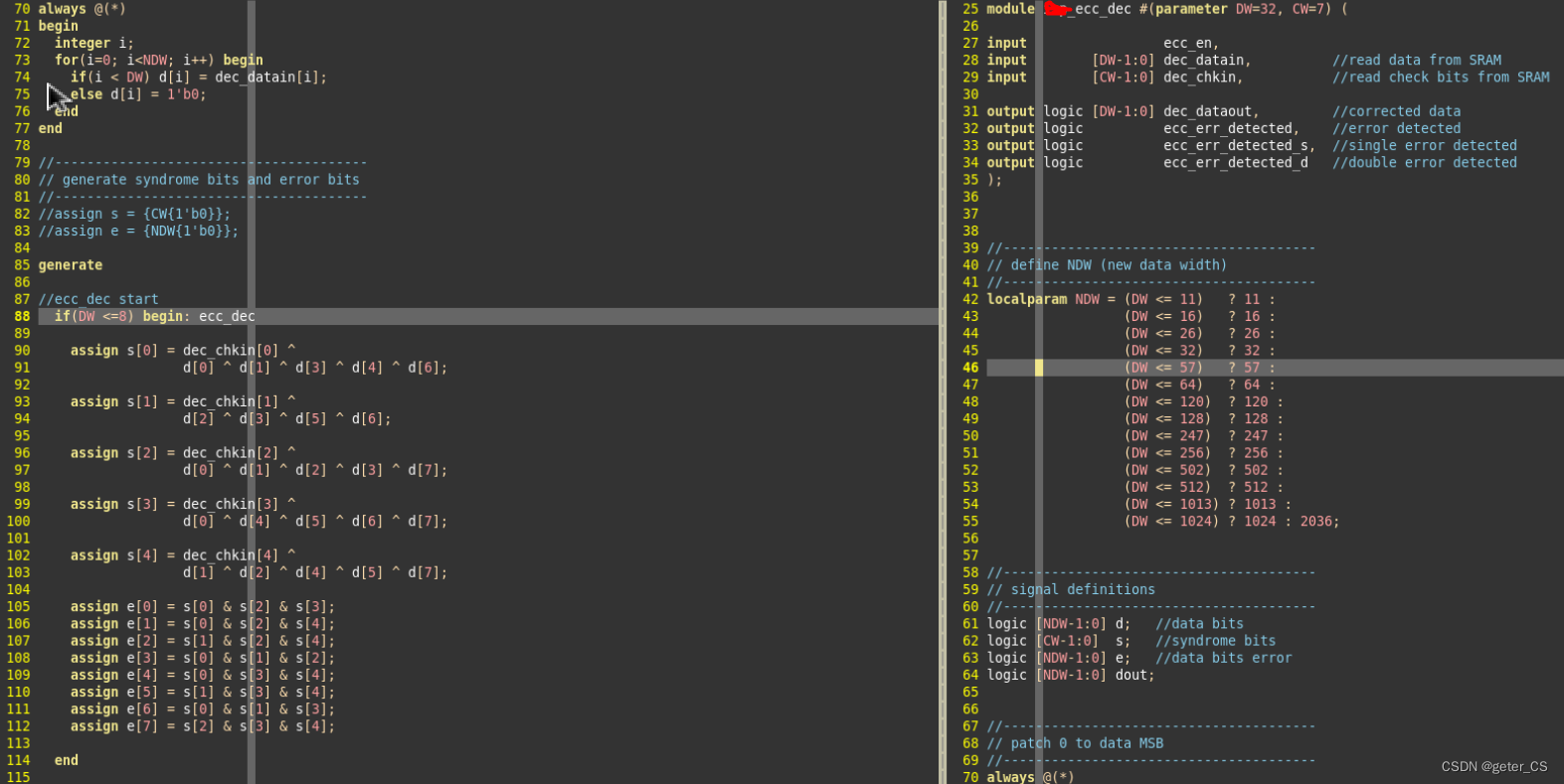
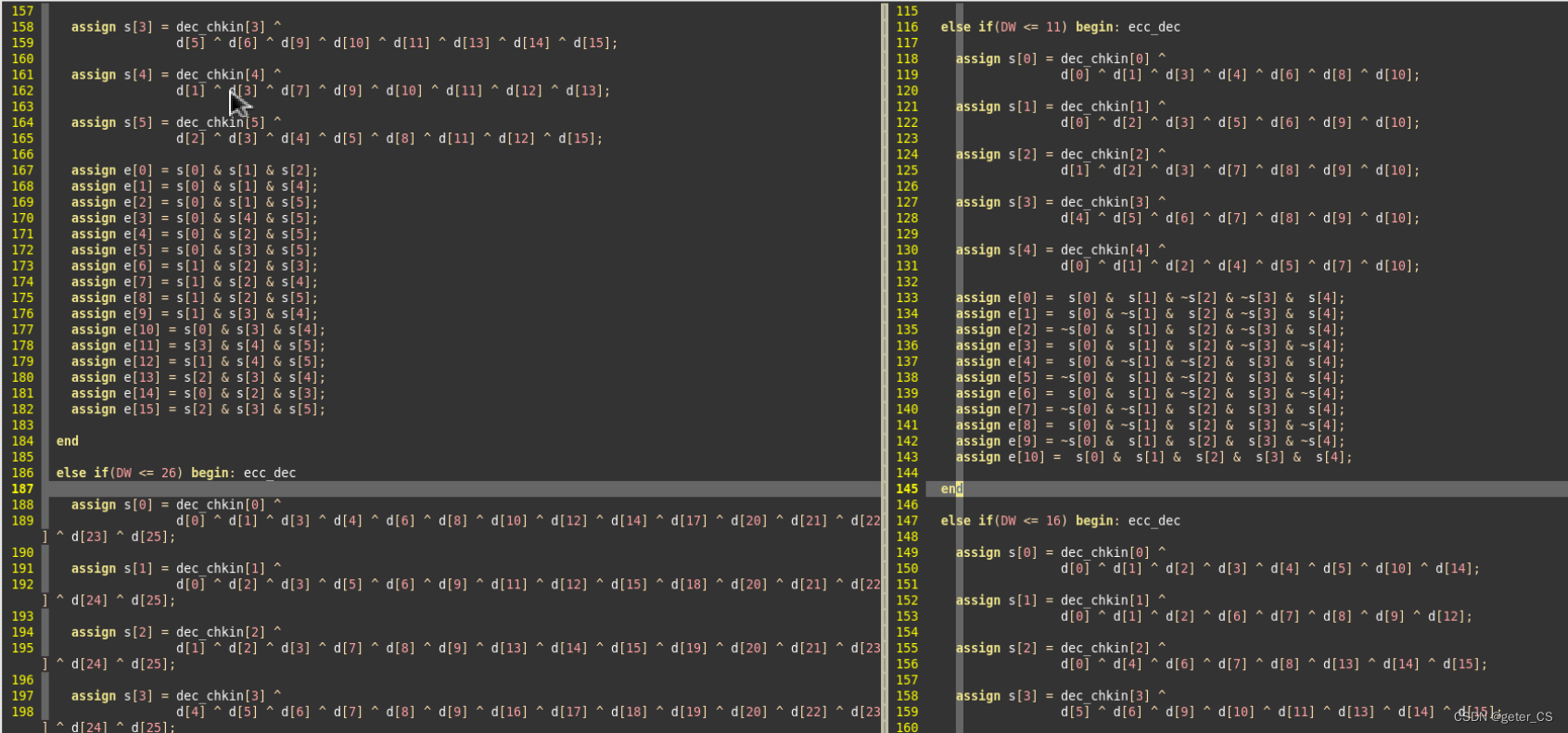
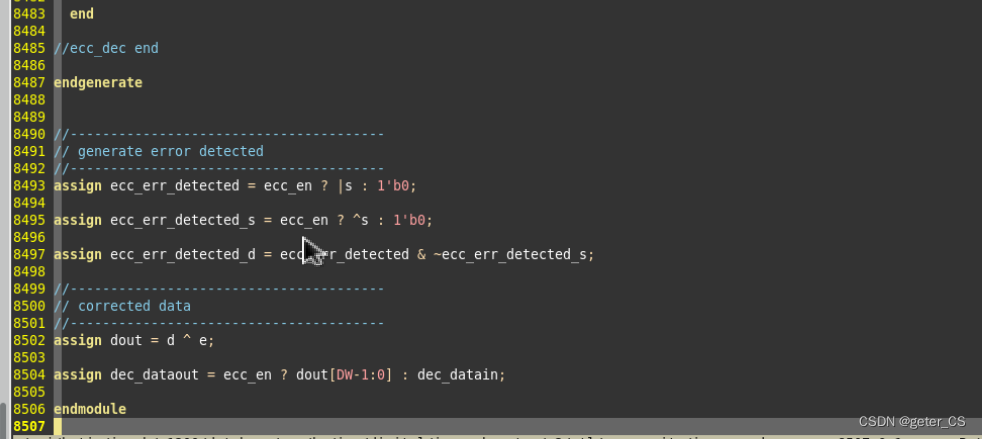
此代码是偶校验的,校验原理是:校验位和数据位的异或结果s[i]需要是0,如果不是0说明有错误。在认为只有小于3bit出错的情况下,此算法的工作会认为:
s中存在bit为1,那么说明有错误,ecc_err_detected拉高
如果s异或结果为1,那么说明有一bit错误,
ecc_err_detected和
ecc_err_detected_s都会拉高
s中存在bit为1,那么说明有错误,ecc_err_detected拉高,且
s异或结果为0,那么说明不是1 bit错误,
ecc_err_detected和
ecc_err_detected_d都会拉高
超过3个bit(包括3bit)后此代码不能纠正也不能判断出错位数,只能判断出错位数的奇偶性。
此代码的纠正原理是:e[0]表示d[0]所在属的三个校验位c[0],c[2],c[3]的校验结果s[0],s[2],s[3]的取&,如果为1表示三个校验位都出错,(按照上面图形解释思想)同时属于这三个校验位的只有d[0],那么就表示d[0]出错了。最后矫正时d[0]^e[0]就是,如果d[0]出错,出错后为0,那么0^1=1,如果出错后为1,那么1^1=0.这样就可以矫正。