C++ -- AVL树插入实现和测试

news2024/12/1 2:24:55

文章目录

  • 1. AVL树概念
  • 2. AVL树满足性质
  • 3. AVL节点结构
  • 4. 插入操作
  • 5. 检测
  • 6. 完整代码

1. AVL树概念

AVL树就是自平衡二叉查找树，为了解决二叉树退化为单链表，使得增删查改时间度为O(N)，这里采用控制平衡策略达到效率是O(logN)。

2. AVL树满足性质

  • 每个节点的左右子树高度之差绝对不能超过1
    • 左边插入（父节点高度差-1）
    • 右边插入（父节点高度差+1）
    • 不插入（自身节点高度差为0）

3. AVL节点结构

template <class KEY, class VAULE>
struct AVLtree_node
{
	AVLtree_node<KEY, VAULE>* _left; //左节点指向
	AVLtree_node<KEY, VAULE>* _right; //右节点指向
	AVLtree_node<KEY, VAULE>* _parent; //父节点指向

	pair<KEY, VAULE> _couple; //存储key/value
	int _balanceFactor; //平衡因子(左右子树高度差)

	AVLtree_node(const pair<KEY, VAULE>& couple)
		:_left(nullptr)
		:_right(nullptr)
		:_parent(nullptr)
		:_couple(couple)
		:_balanceFactor(0)
	{}
};

4. 插入操作

  1. 插入阶段
    1. 根节点为空
      1. new节点，改变根指向，返回true
    2. 根节点不为空
      1. 找到插入位置
        1. 右查找：当前节点key值 < 插入节点key值
        2. 左查找：当前节点key值 > 插入节点key值
        3. 当前节点key值 = 插入节点key值 ：直接返回false
      2. 在对应待插入位置插入
        1. new节点，当前插入位置指向该节点
        2. 右插入：当前节点key值 < 插入节点key值
        3. 左插入: 当前节点key值 > 插入节点key值
      3. 当前被插入节点父指针指向指向被连接节点
      4. 自动平衡（TODO）
bool insert(const pair<KEY, VAULE>& couple)
{
    //二叉搜索树阶段
	if (_root == nullptr) //根为空:直接new并指向返回
	{
		_root = new node(couple);
		return true;
	}

	/*找插入位置*/
	node* parent = nullptr; //起初根节点的父节点为nullptr
	node* cur = _root; //被插入节点指向
	while (cur)
	{
		if (cur->_couple.first < couple.first) //右查找：当前节点key值 < 插入节点key值
		{
			parent = cur;
			cur = cur->_right;
		}
		else if (cur->_couple.first > couple.first) //左查找: 当前节点key值 > 插入节点key值
		{
			parent = cur;
			cur = cur->_left;
		}
		else //当前节点key值 = 插入节点key值：直接退出
		{
			return false;
		}
	}

	/*在对应位置插入*/
	cur = new node(couple);
	if (parent->_couple.first > couple.first) //左插入: 当前节点key值 > 插入节点key值
	{
		parent->_left = newnode;
	}
	else //右插入：当前节点key值 < 插入节点key值
	{
		parent->_right = newnode;
	}
	cur->_parent = parent; //反向链接

	/*自动平衡 TODO*/
    //AVL树阶段

}
  1. 平衡阶段铺垫

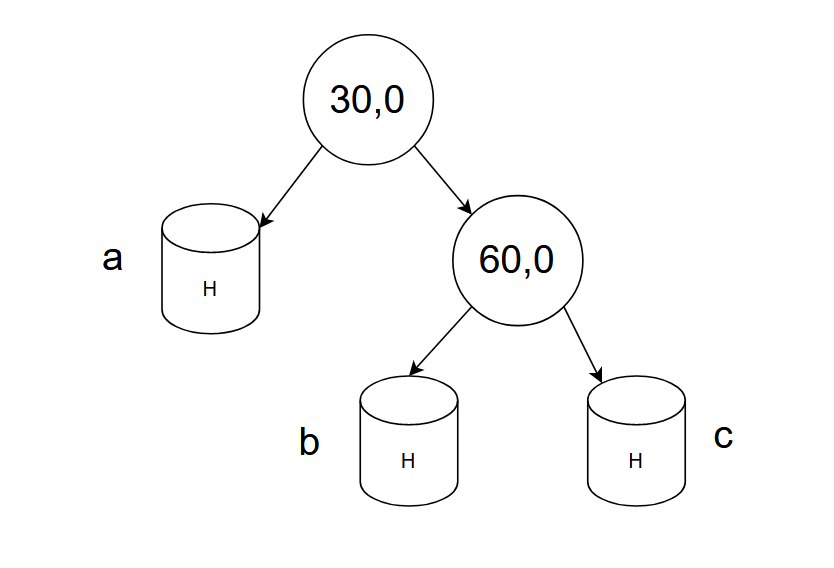
注意：并没有画上父节点指向，为了便于观察所以没有画，默认每个节点是有父节点指向的

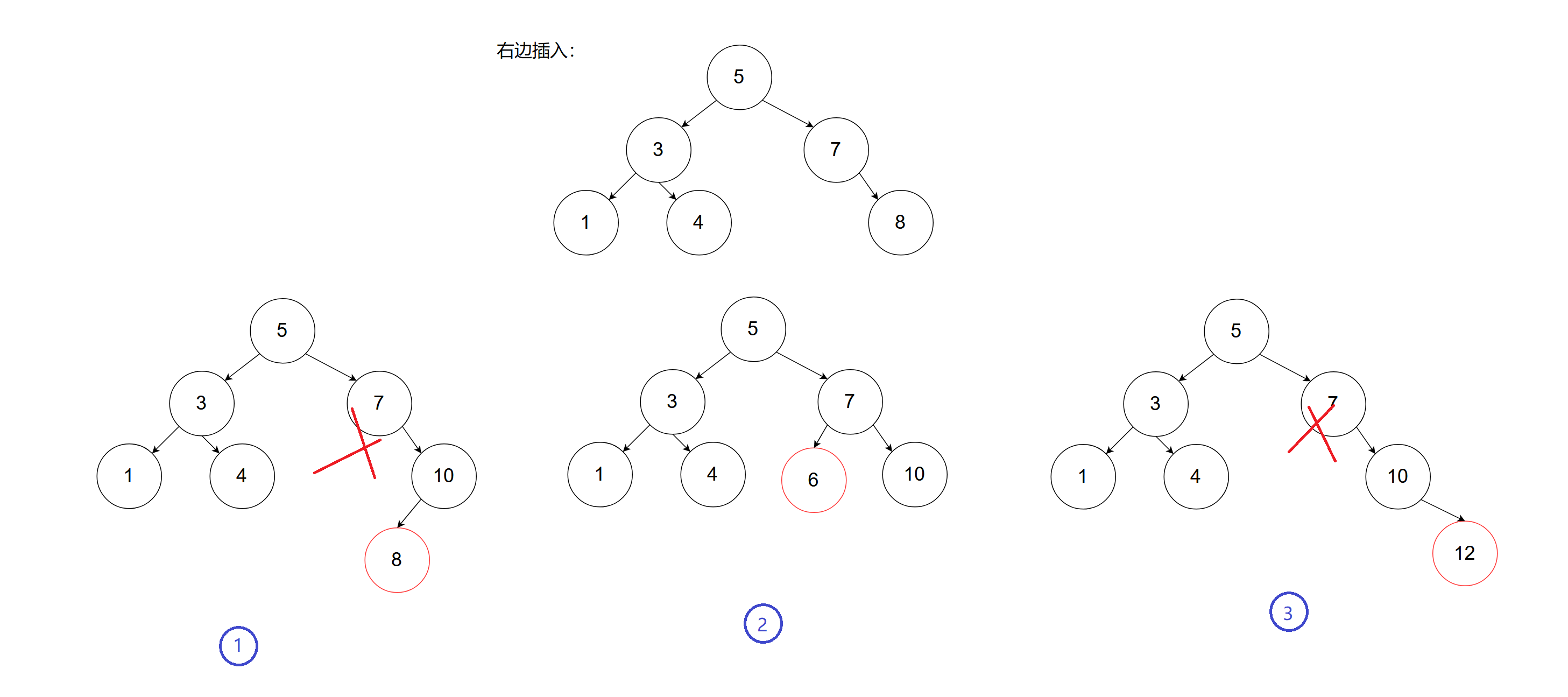
  • 右边插入构图
  • 左边插入构图

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-rGLjZnpU-1684114665514)(https://typora130.oss-cn-nanjing.aliyuncs.com/QQ截图20230513154519.png)]

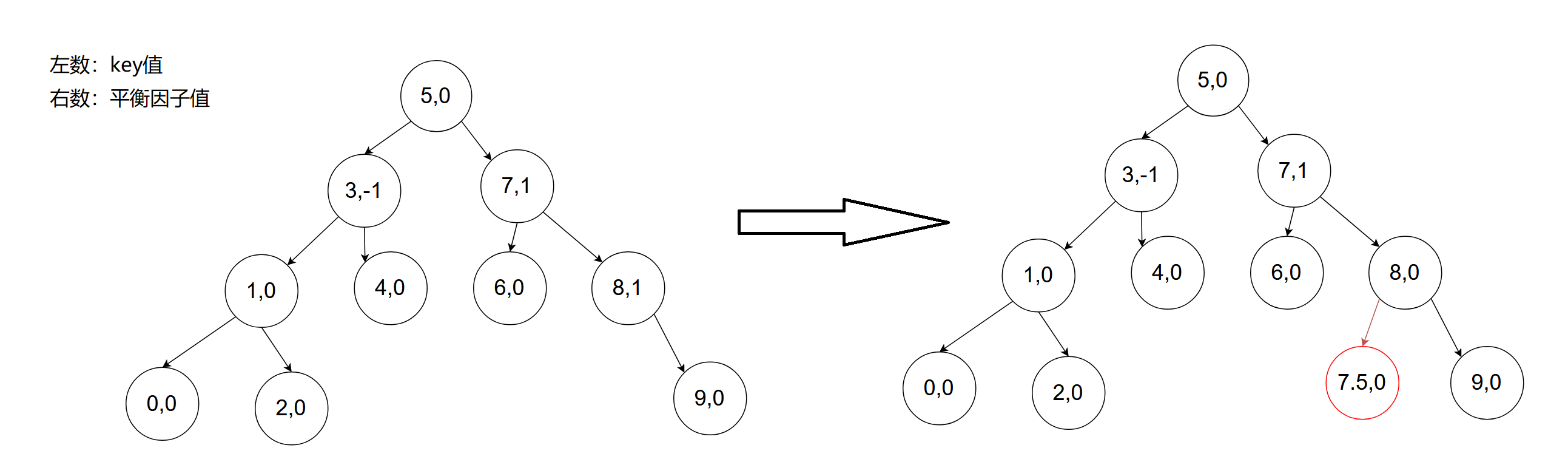
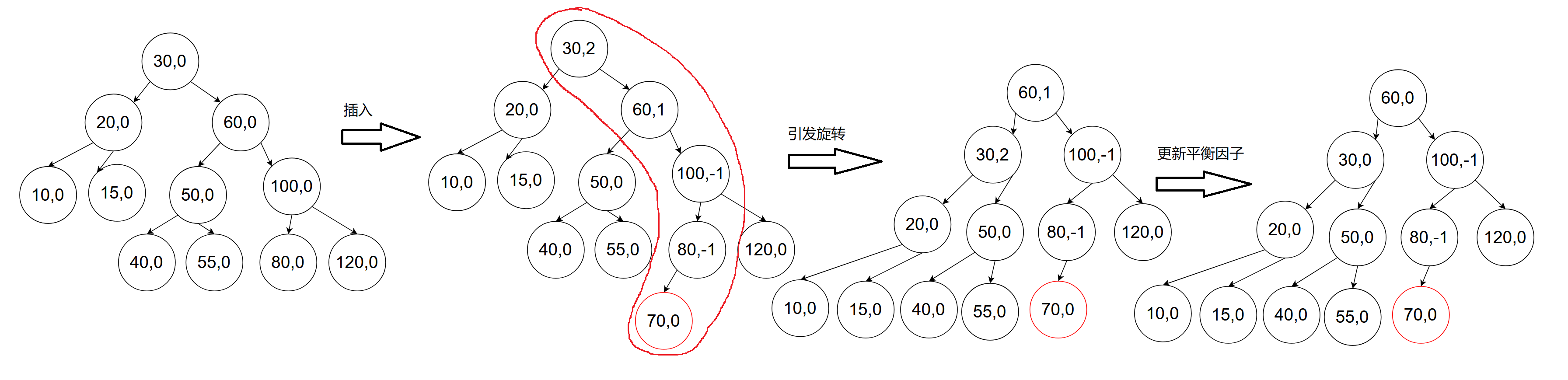
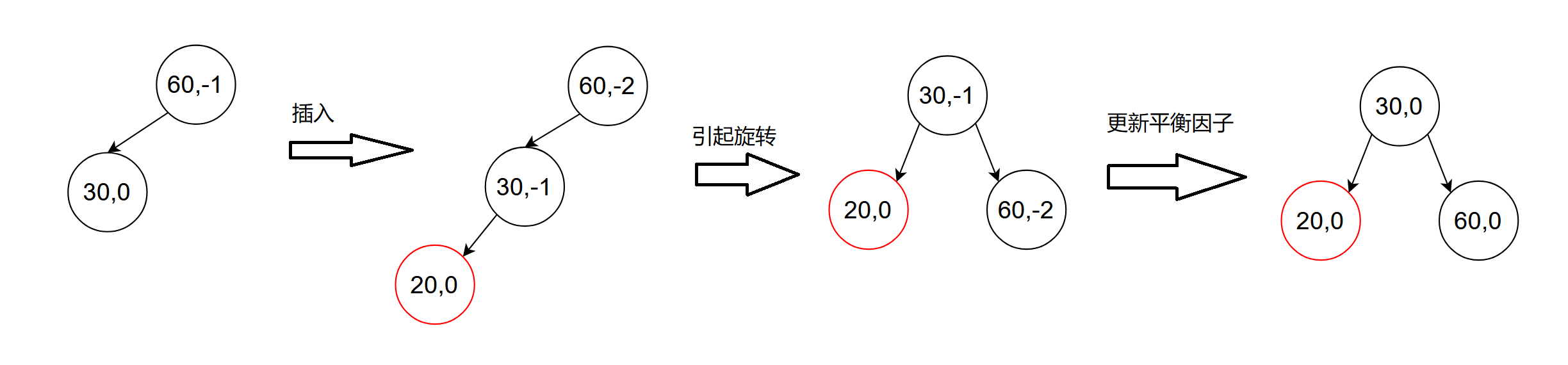
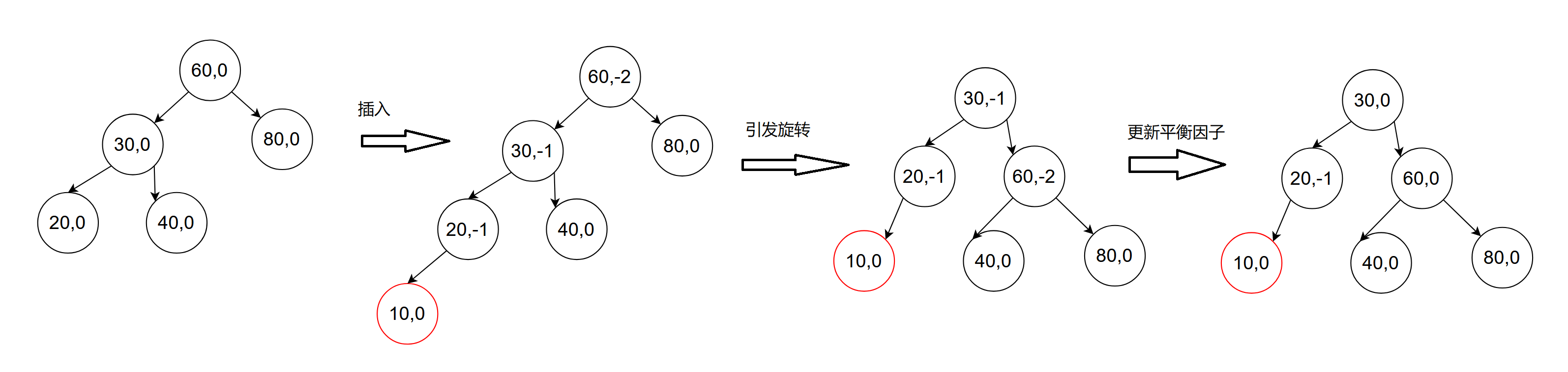
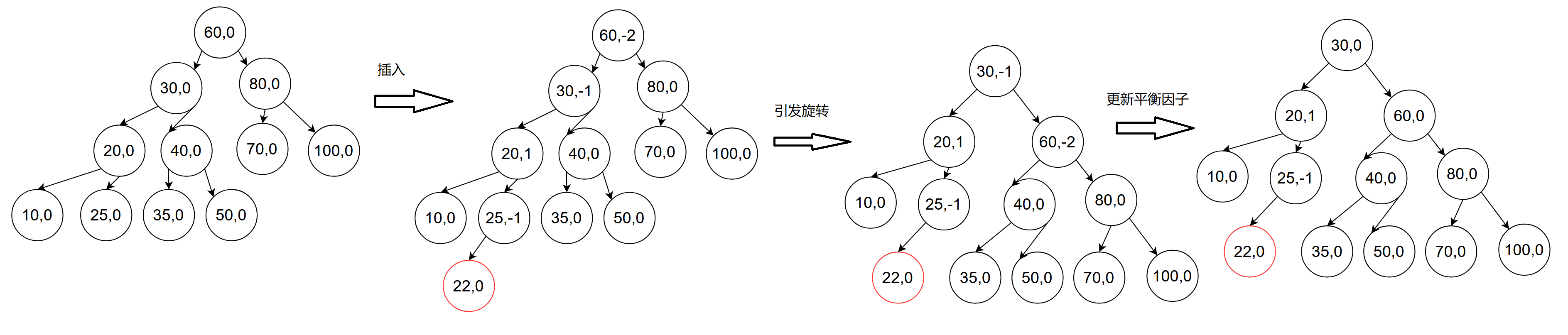
上面左右插入构图示范中，观察发现该节点左右子树高度差超过了1就会形成子树单链表，这样就会影响到效率，那么这里的解决办法就是对其旋转处理（待解），另外观察到上面错误高度差情况，会发现一旦插入其被插入节点的部分祖先的平衡因子（高度差）可能改变，所以，插入新增节点会影响部分或全部祖先的平衡因子，平衡因子怎么来更新呢？如果新增节点在其父节点左边，父节点平衡因子-1，如果新增节点在其父节点右边，父节点平衡因子+1，每个节点的平衡因子初始状态都是0。是什么时候平衡因子更新？当插入节点的父节点的平衡因子变化（不为0），那么就需要对其被插入节点的部分或者全部祖先的平衡因子更新。

观察：右边插入三种情况示范：

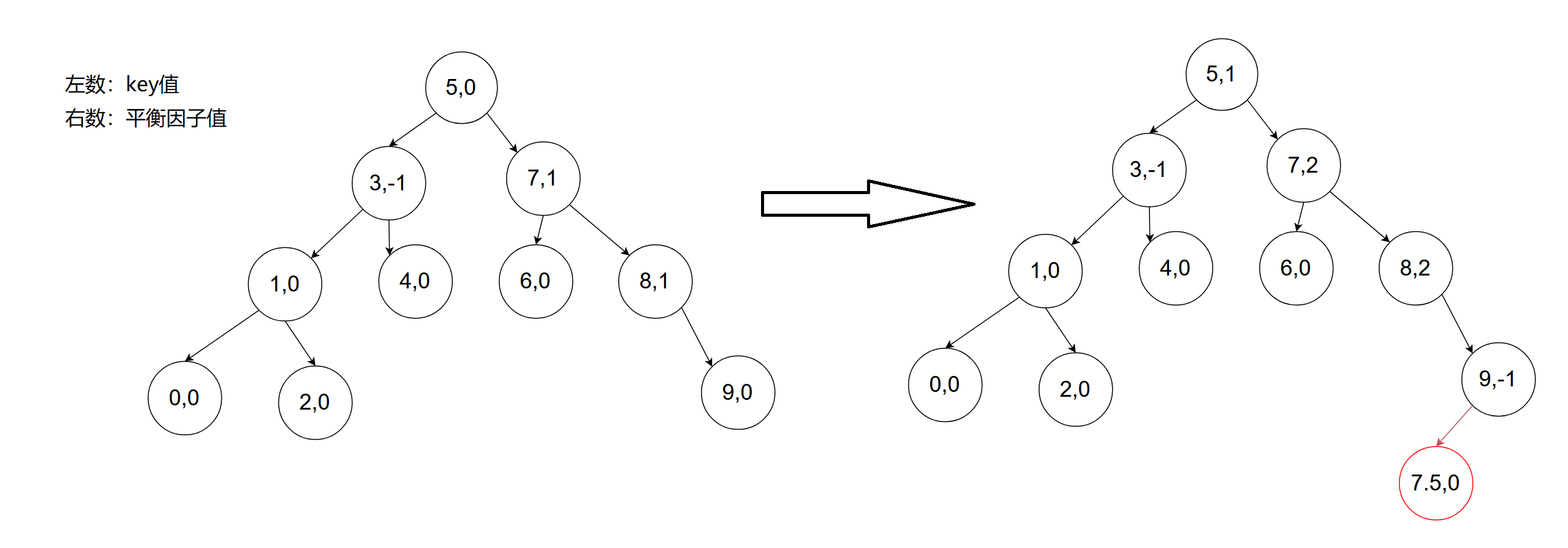
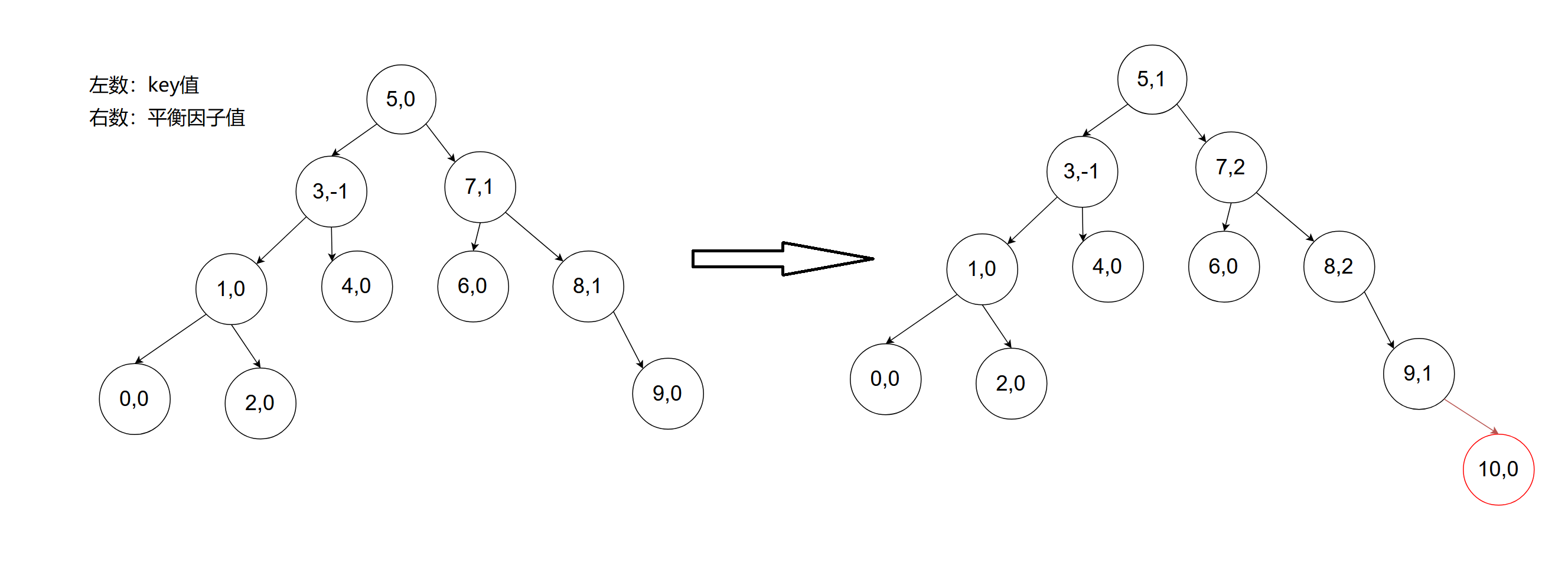
被插入节点父节点平衡高度不为0，就向上更新祖先的平衡因子，向上更新的依据是该节点左右子树高度变化了；如果插入节点父节点平衡高度为0，就无需向上更新平衡因子

后面两种情况观察：当祖先节点的平衡因子为2或者-2时，就不应该再往上层更新平衡因子了（key值为7的节点的平衡因子就没必要更新了），因为此时只要有一个祖先的平衡因子为2说明就已经有问题了，就需要对这部分子树来调整达到一种平衡状态（旋转处理）。

  1. 自动平衡
    1. 更新平衡因子
      1. 改变被插入节点父节点平衡因子
        1. 被插入节点在其父节点右子树中：父节点平衡因子+1
        2. 被插入节点在其父节点左子树中：父节点平衡因子-1
      2. 判断是否继续向上更新平衡因子
        1. 父节点平衡因子为1或者-1，继续更新
        2. 父节点平衡因子为0，无需更新
        3. 父节点平衡因子为2或者-2，子树不平衡，旋转处理使得平衡（TODO）
bool insert(const pair<KEY, VAULE>& couple)
{
	if (_root == nullptr) //根为空:直接new并指向返回
	{
		_root = new node(couple);
		return true;
	}

	/*找插入位置*/
	node* parent = nullptr; //起初根节点的父节点为nullptr
	node* cur = _root; //被插入节点指向
	while (cur)
	{
		if (cur->_couple.first < couple.first) //右查找：当前节点key值 < 插入节点key值
		{
			parent = cur;
			cur = cur->_right;
		}
		else if (cur->_couple.first > couple.first) //左查找: 当前节点key值 > 插入节点key值
		{
			parent = cur;
			cur = cur->_left;
		}
		else //当前节点key值 = 插入节点key值：直接退出
		{
			return false;
		}
	}

	/*在对应位置插入*/
	cur = new node(couple);
	if (parent->_couple.first > couple.first) //左插入: 当前节点key值 > 插入节点key值
	{
		parent->_left = newnode;
	}
	else //右插入：当前节点key值 < 插入节点key值
	{
		parent->_right = newnode;
	}
	cur->_parent = parent; //反向链接

	/*自动平衡 TODO*/

	//更新平衡因子
	while (parent)
	{
		if (cur == parent->_right) //被插入节点在其父节点右子树中
		{
			parent->_balanceFactor++;
		}
		else //被插入节点在其父节点左子树中
		{
			parent->_balanceFactor--;
		}

		if (parent->_balanceFactor == 1 || parent->_balanceFactor == -1) //继续更新平衡因子
		{
			parent = parent->_parent;
			cur = cur->_parent;
		}
		else if (parent->_balanceFactor == 0) //无需更新
		{
			break;
		}
		else if (parent->_balanceFactor == 2 || parent->_balanceFactor == -2) //子树不平衡(旋转处理)
		{
			/*TODO*/
            
            break; //旋转之后达到平衡无需更新平衡因子(操作完后便知)
		}
		else
		{
			assert(false);
		}
	}
}
  1. 平衡阶段旋转处理

旋转目的：让子树平衡并且降低子树高度

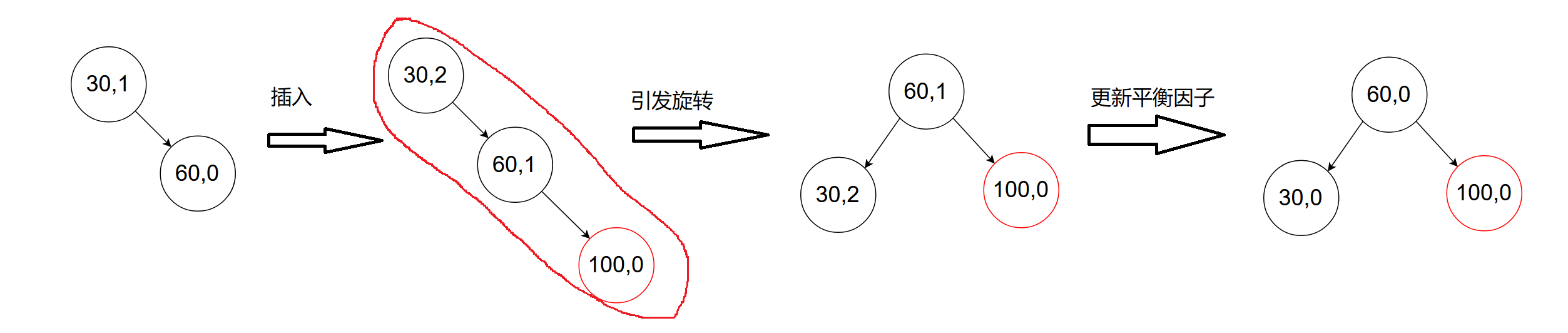
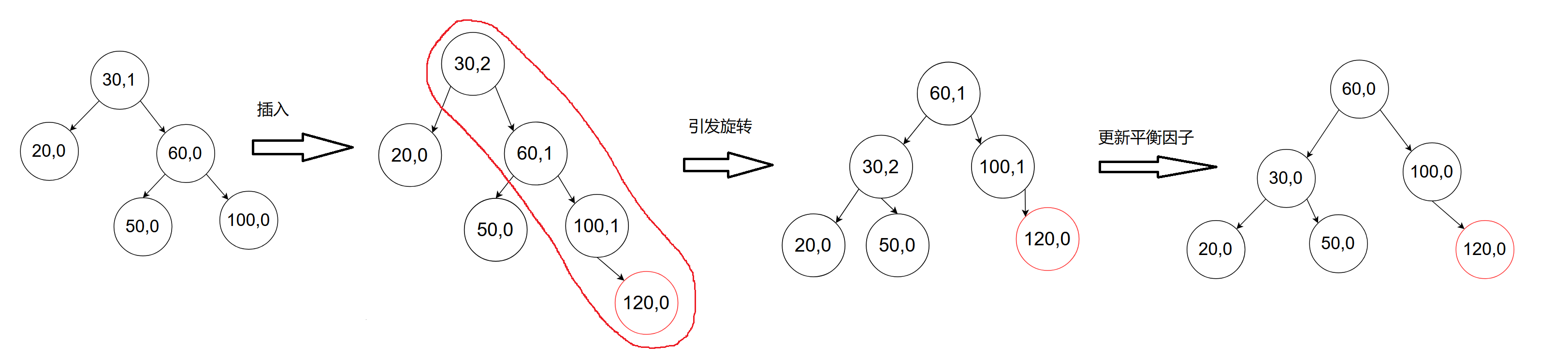
  • 左单旋

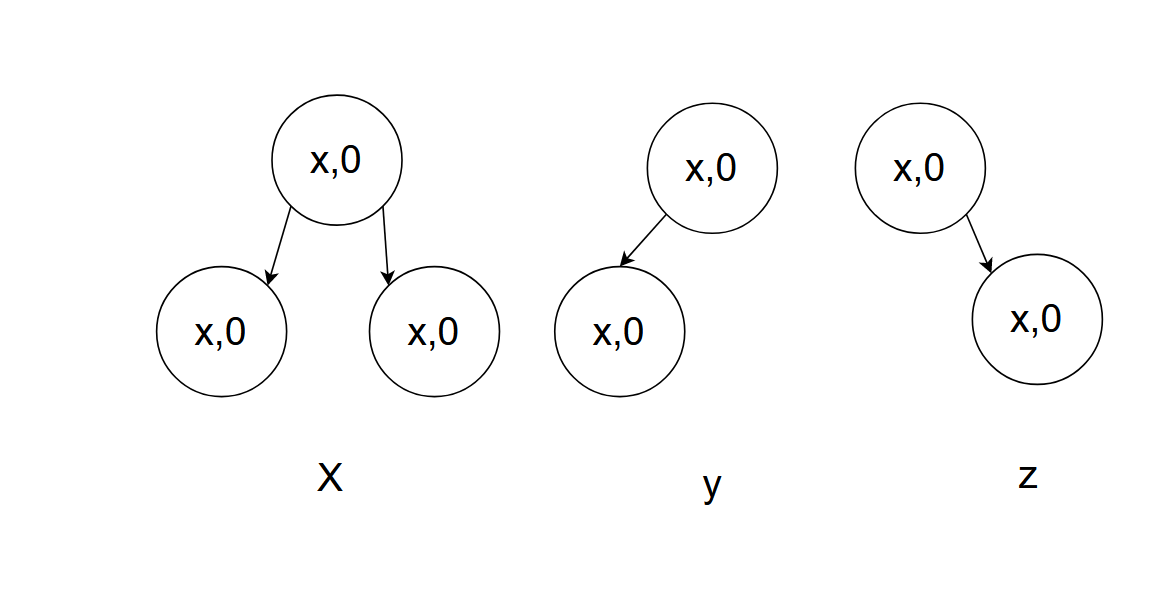
左单旋一定是右高左低

三个举例：

三个举例来抽象得到宏观图：

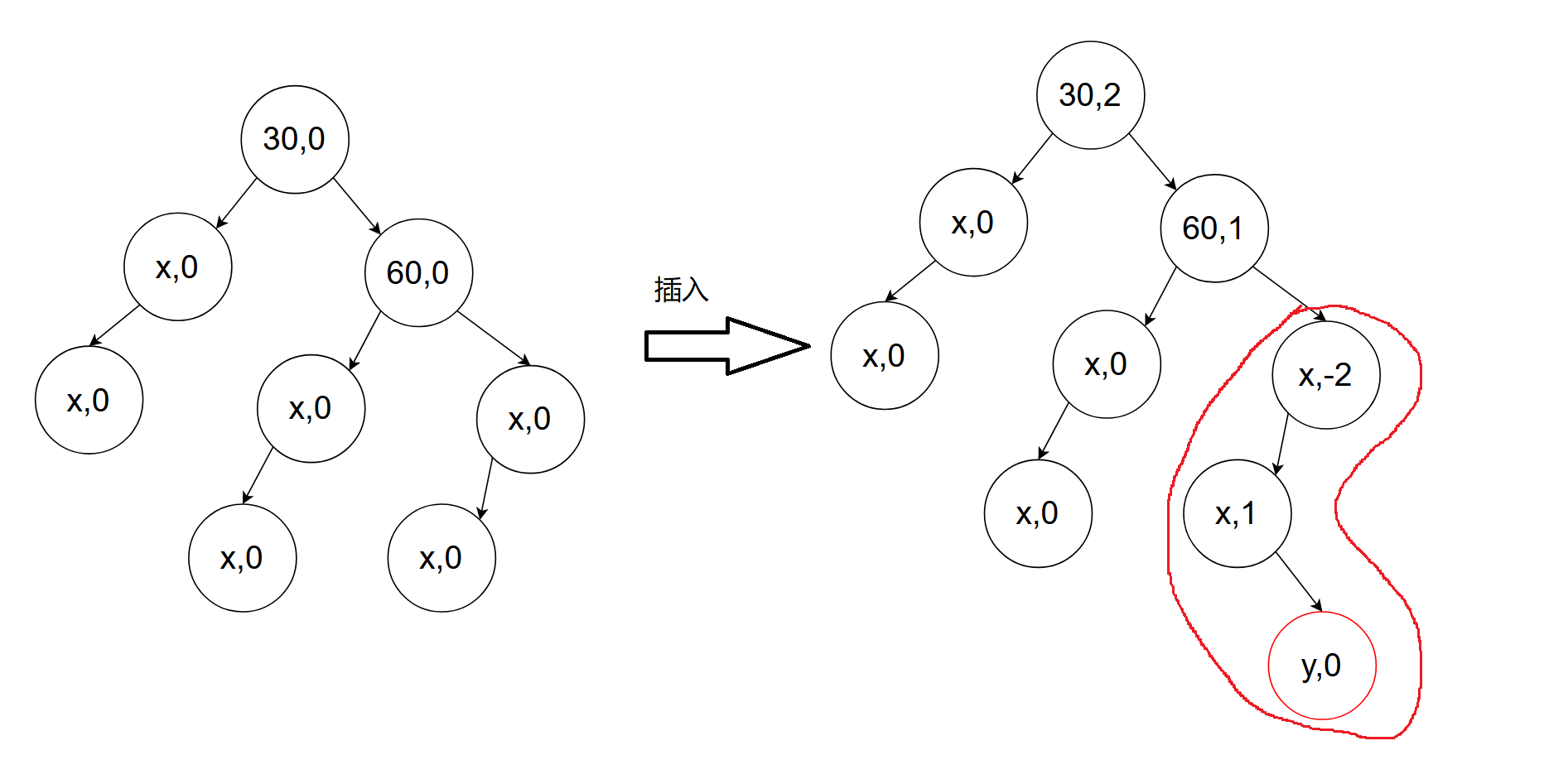
H为这颗子树高度，当H为0，反应就是上述第一个例子；当H为1，反应就是上述第二个例子；当H为2，反应就是上述第三个例子。当H为x时，其调整方法不变。当H为2时，此时有三种情况的高度为2的树：

但是这里c这棵子树必须是x类型的高度为2的树，a,b这两课子树可以是任意一种都可以。为什么c子树必须是x类型的树呢？如果是y型可能插入不会引发旋转，也可能只会局部旋转：

如何旋转？

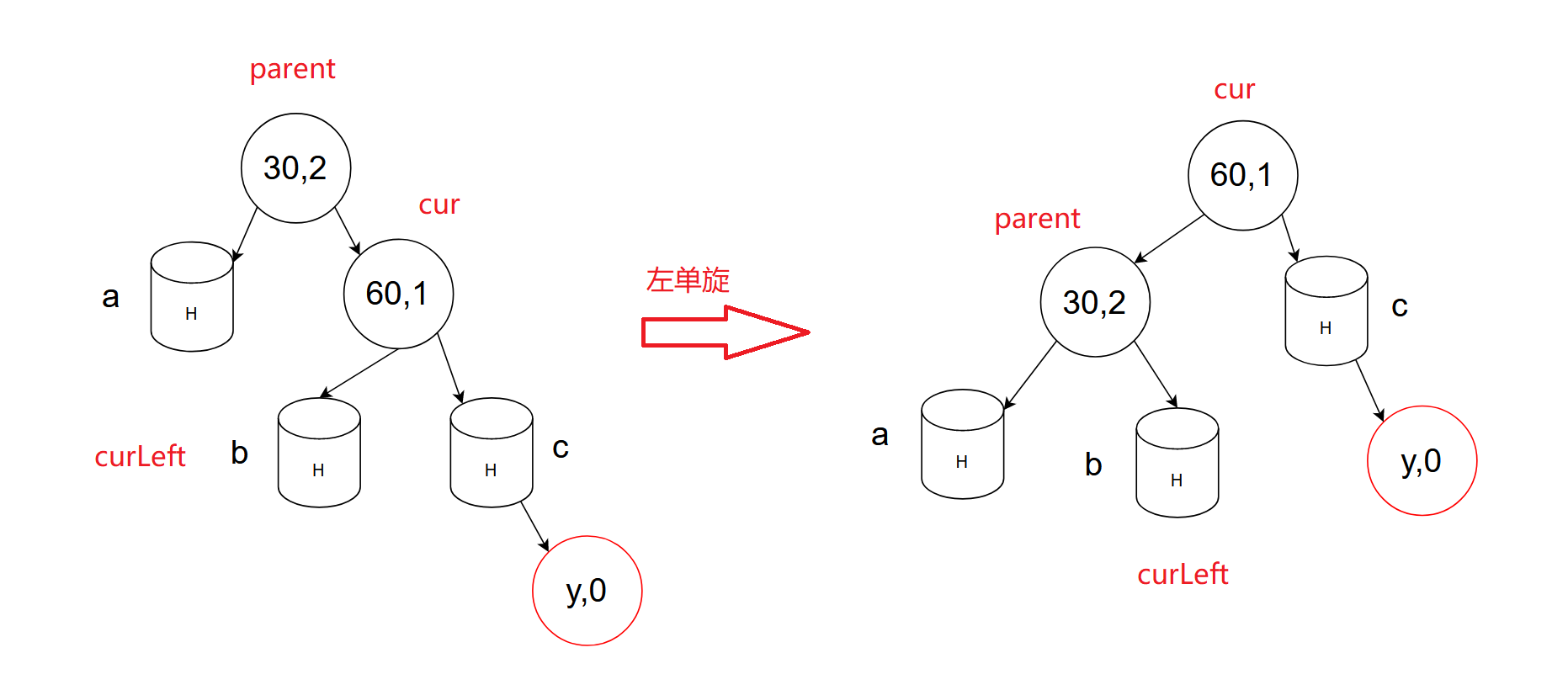
  1. 让cur的左子树(curLeft)放在parent的右子树位置并且curLeft的父节点指向指向parent
  2. 让parent放在cur的左子树位置并且parent的父节点指向指向cur
  3. cur变为子树或者整颗树的根
  4. 更新parent和cur的平衡因子
//parent->_balanceFactor == 2 && cur->_balanceFactor = 1
void leftSingleRotate(node* parent) //左单旋
{
	//记录指针
	node* parent_RightChild = parent->_right; //parent_RightChild = cur
	node* parent_RightChild_LeftChild = parentRightChild->_left; //parent_RightChild_LeftChild = curLeft
	node* parent_parent = parent->_parent; //局部根或整棵树根的父节点

	parent->_right = parent_RightChild_LeftChild; //让cur的左子树(curLeft)放在parent的右子树位置
	if (parent_RightChild_LeftChild != nullptr) //H为0时,parent_RightChild_LeftChild=nullptr
	{
		parent_RightChild_LeftChild->_parent = parent; //curLeft的父节点指向指向parent
	}
	parent_RightChild->_left = parent; //让parent放在cur的左子树位置
	parent->_parent = parent_RightChild; //parent的父节点指向指向cur

	//cur(parent_RightChild)变为子树或者整颗树的根
	if (parent_parent == nullptr) //parent是整颗树的根
	{
		_root = parent_RightChild;
		_root->_parent = nullptr;
	}
	else //parent是局部子树的根
	{
		if (parent_parent->_left == parent) //parent节点在父节点的左子树位置
		{
			parent_parent->_left = parent_RightChild;
		}
		else //parent节点在父节点的右子树位置
		{
			parent_parent->_right = parent_RightChild;
		}
		parent_RightChild->_parent = parent_parent;
	}

	//更新平衡因子
	parent->_balanceFactor = parent_RightChild->_balanceFactor = 0;
}
  • 右单旋

右单旋一定是左高右低

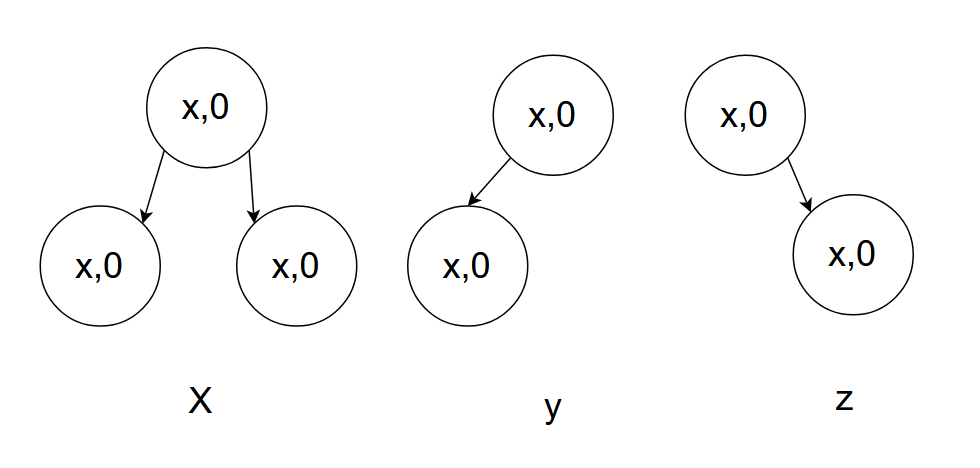
三个举例来抽象得到宏观图：

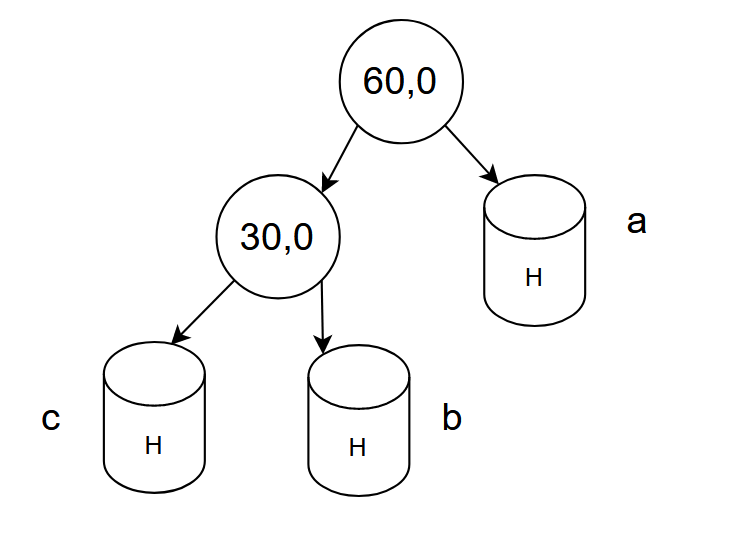
H为这颗子树高度，当H为0，反应就是上述第一个例子；当H为1，反应就是上述第二个例子；当H为2，反应就是上述第三个例子。当H为x时，其调整方法不变。当H为2时，这里的c子树必须是x类型的树，此时有三种情况的高度为2的树：

如何旋转？

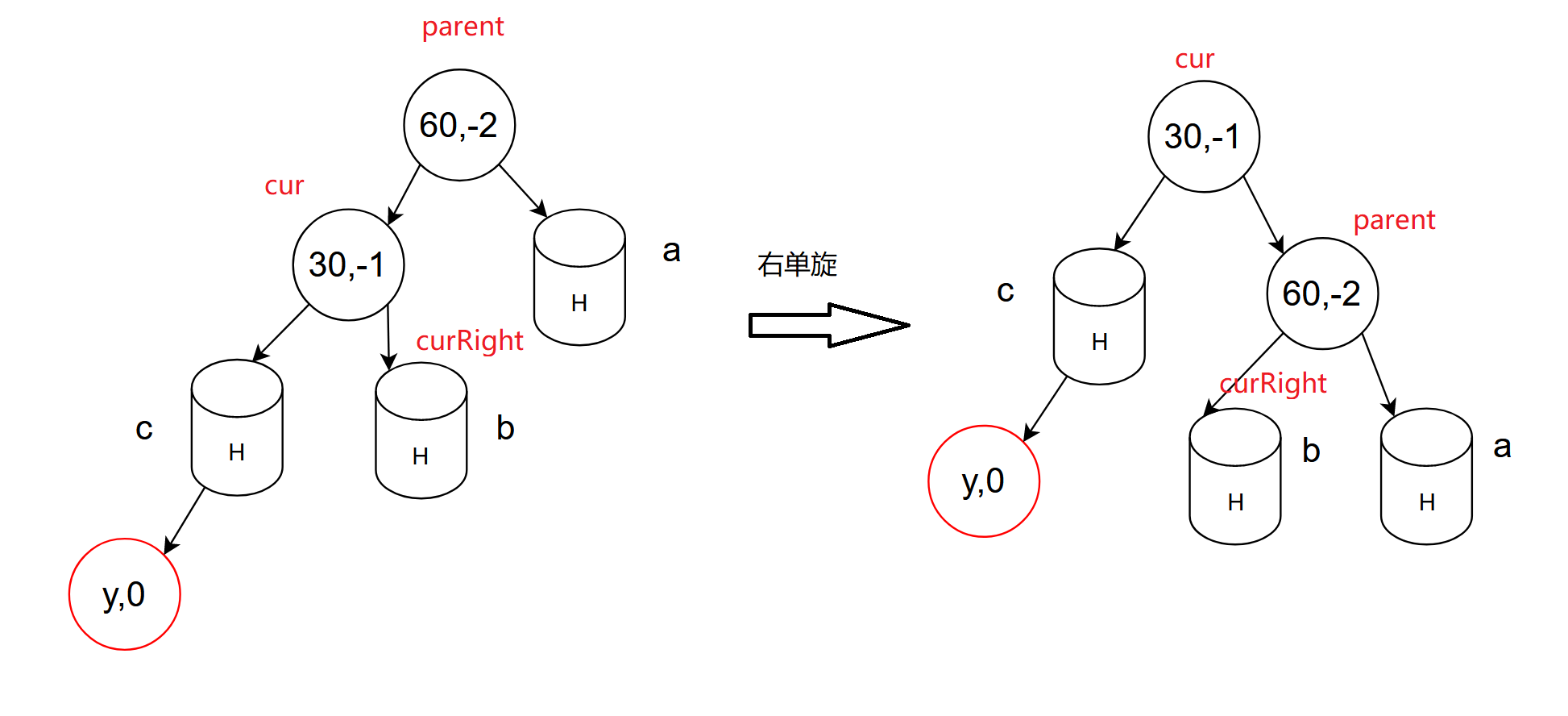
  1. 让cur的右子树(curRight)放在parent的左子树位置并且让curRight父节点的指向指向parent
  2. 让parent放在cur的右子树位置并且让parent的父节点指向指向cur
  3. cur变为子树或者整颗树的根
  4. 更新parent和cur的平衡因子
//parent->_balanceFactor == -2 && cur->_balanceFactor == -1
void rightSingleRotate(node* parent) //右单旋
{
    //记录指针
    node* parent_LeftChild = parent->_left; //parent_LeftChild = cur
    node* parent_LeftChild_RightChild = parent_LeftChild->_right; //parent_LeftChild_RightChild = curRight
    node* parent_parent = parent->_parent; //局部根或整棵树根的父节点

    parent->_left = parent_LeftChild_RightChild; //让cur的右子树(curRight)放在parent的左子树位置
    if (parent_LeftChild_RightChild != nullptr)
    {
        parent_LeftChild_RightChild->_parent = parent; //让curRight父节点的指向指向parent
    }
    parent_LeftChild->_right = parent; //让parent放在cur的右子树位置
    parent->_parent = parent_LeftChild; //让parent的父节点指向指向cur

    //cur(parent_LeftChild)变为子树或者整颗树的根
    if (parent_parent == nullptr) //parent是整颗树的根
    {
        _root = parent_LeftChild; //cur(parent_LeftChild)就是根
        _root->_parent = nullptr;
    }
    else //parent是局部子树的根
    {
        if (parent_parent->_left == parent) //parent节点在父节点的左子树位置
        {
            parent_parent->_left = parent_LeftChild;
        }
        else //parent节点在父节点的右子树位置
        {
            parent_parent->_right = parent_LeftChild;
        }
        parent_LeftChild->_parent = parent_parent; //cur(parent_LeftChild)指向局部根的父节点
    }

    //更新平衡因子
    parent->_balanceFactor = parent_LeftChild->_balanceFactor = 0;
}
  • 先左后右旋

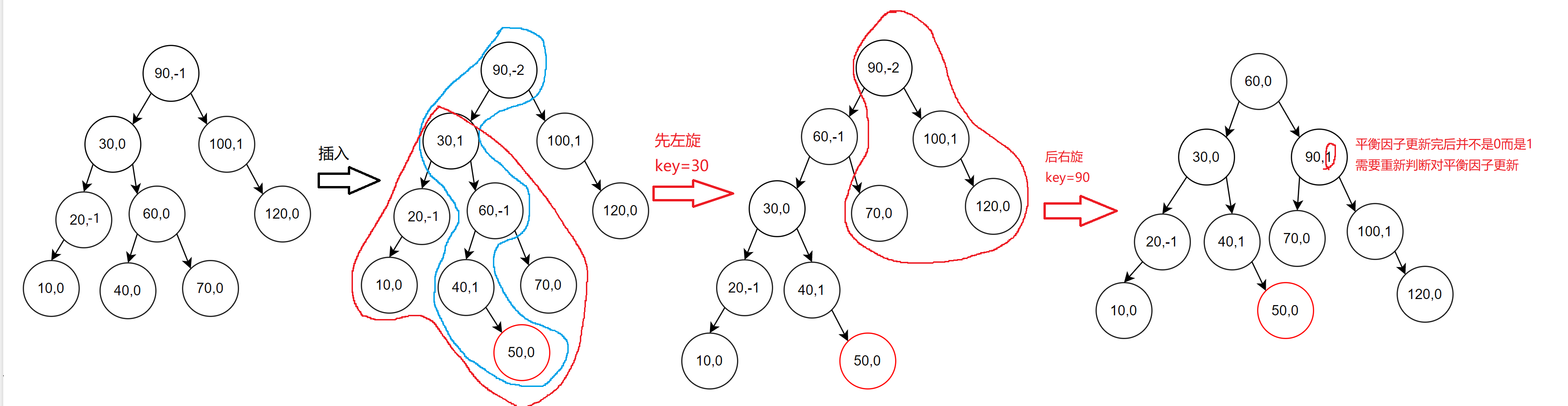
抽象图：

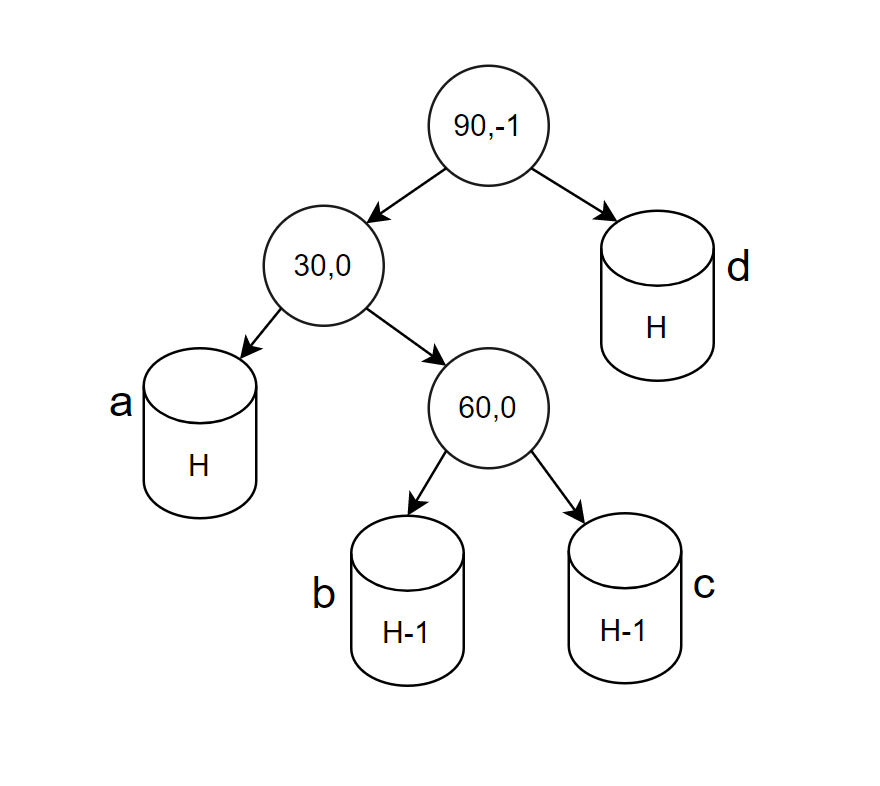
H为子树高度，H为0时，此时60这个节点也不存在，新增节点必须是key为60这个节点位置；H为1，2，3…等等图形这里不再画出，都可以通过抽象达成相同调整方法，这里被插入节点一定是b，c子树位置或者b，c的子树孩子位置。

如何旋转？

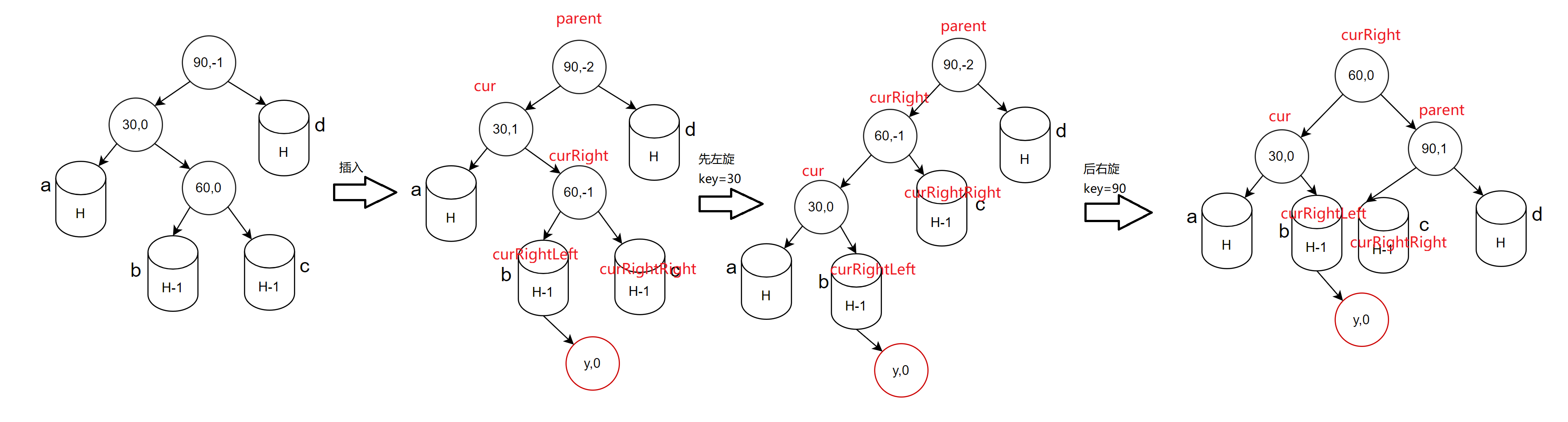
  1. 先左旋cur为根的子树
    1. 让cur的右指向指向curRightLeft并且curRightLeft的父节点的指向指向cur
    2. 让curRight的左指向指向cur并且cur的父节点的指向指向curRight
    3. curRight作为子树根并且改变curRight的父节点的指向指向parent
    4. 更新cur和curRight的平衡因子为0
  2. 后右旋parent为根的子树
    1. 让parent的左指向指向curRightRight并且curRightRight的父节点的指向指向parent
    2. 让curRight的右子树指向parent并且parent的父节点的指向指向curRight
    3. curRight作为树的根并且改变curRight的父节点指向指向空
    4. 更新parent和curRight的平衡因子为0
  3. 更新cur、curRight、parent平衡因子（插入b，c子树不同位置会导致最终平衡因子的变化）
    1. c子树插入(curRight->_balanceFactor=1)：最终cur的平衡因子为-1，parent平衡因子为0，curRight平衡因子为0
    2. b子树插入(curRight->_balanceFactor=-1)：最终cur的平衡因子为0，parent平衡因子为1，curRight平衡因子为0
    3. curRight本身是被插入节点(curRight->_balanceFactor=0，H=0)，最终cur、parent、curRight平衡因子都为0
//parent->_balanceFactor == -2 && cur->_balanceFactor == 1
void leftRightRotate(node* parent)
{
    node* parent_LeftChild = parent->_left; //parent_LeftChild = cur
    node* parent_LeftChild_RightChild = parent_LeftChild->_right; //parent_LeftChild_RightChild = curRight
    int balanceFactor = parent_LeftChild_RightChild->_balanceFactor; //记录curRight的平衡因子值：确定在b子树还是c子树插入

    leftSingleRotate(parent->_left); //左单旋cur为根树
    rightSingleRotate(parent); //右单旋parent为根的树

    //更新cur、curRight、parent平衡因子（插入b，c子树不同位置会导致最终平衡因子的变化）
    if (balanceFactor == 1) //c子树插入
    {
        parent->_balanceFactor = 0;
        parent_LeftChild_RightChild = 0; //curRight->_balanceFactor = 0
        parent_LeftChild = -1; //cur->_balanceFactor = -1
    }
    else if (balanceFactor == -1) //b子树插入
    {
        parent->_balanceFactor = 1;
        parent_LeftChild_RightChild = 0; //curRight->_balanceFactor = 0
        parent_LeftChild = 0;  //cur->_balanceFactor = 0
    }
    else if (balanceFactor == 0) //curRight自身是被插入节点
    {
        parent->_balanceFactor = 0;
        parent_LeftChild_RightChild = 0; //curRight->_balanceFactor = 0
        parent_LeftChild = 0;  //cur->_balanceFactor = 0
    }
    else
    {
        assert(false);
    }
}
  • 先右后左旋

抽象图：

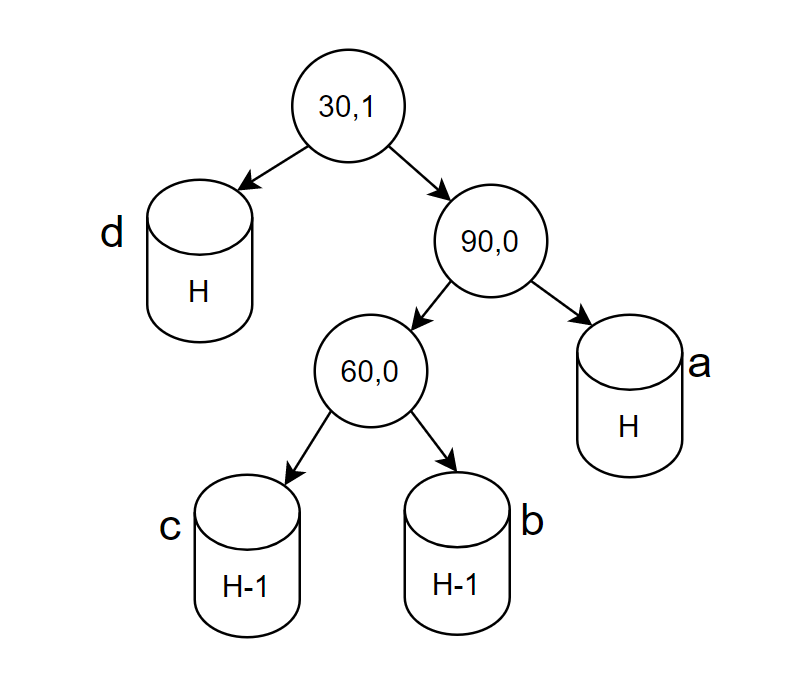
H为子树高度，H为0时，此时60这个节点也不存在，新增节点必须是key为60这个节点位置；H为1，2，3…等等图形这里不再画出，都可以通过抽象达成相同调整方法，这里被插入节点一定是b，c子树位置或者b，c的子树孩子位置。

如何旋转？

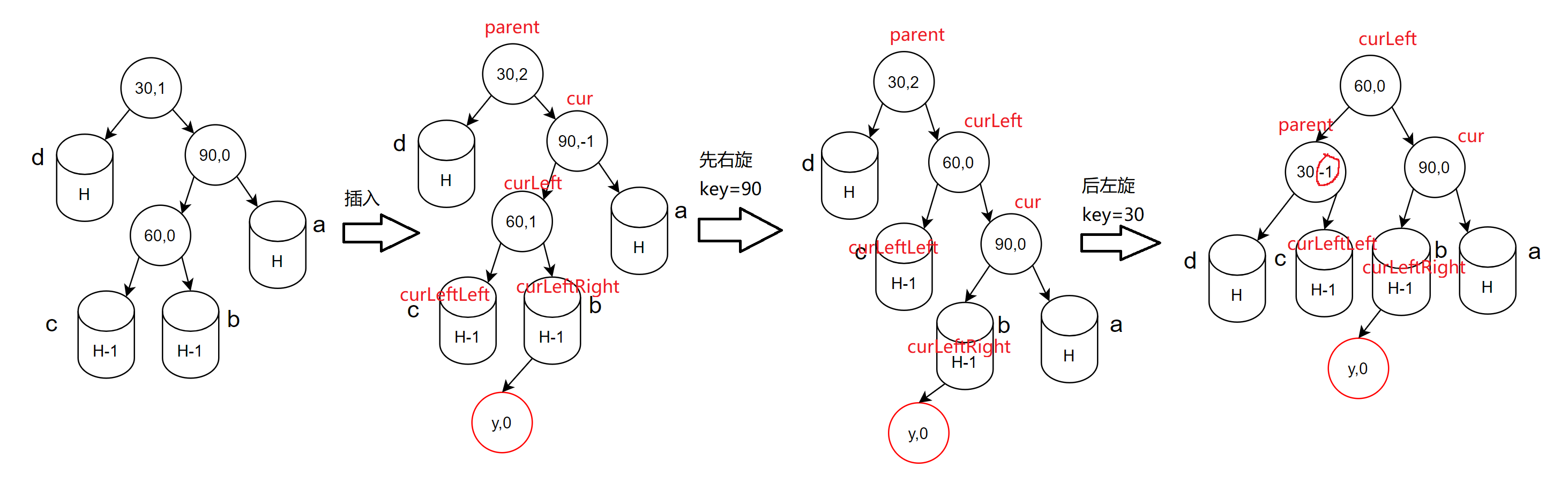
  1. 先右旋cur为根的子树
    1. 让cur的左指向指向curLeftRight并且curLeftRight的父节点的指向指向cur
    2. 让curLeft的右指向指向cur并且cur的父节点的指向指向curLeft
    3. curLeft作为子树的根并且curLeft的父节点的指向指向parent
    4. 更新cur和curLeft的平衡因子为0
  2. 后左旋parent为根的树
    1. 让parent的右指向指向curLeftLeft并且curLeftLeft的父节点的指向指向parent
    2. 让curLeft的左指向指向parent并且paren的父节点的指向指向curLeft
    3. curLeft作为树的根并且改变curLeft的父节点的指向指向nullptr
    4. 更新parent和curLeft的平衡因子为0
  3. 更新cur、curLeft、parent平衡因子（插入b，c子树不同位置会导致最终平衡因子的变化）
    1. b子树插入(curLeft->_balance=1)，最终cur的平衡因子为0，parent平衡因子为-1，curLeft平衡因子为0
    2. c子树插入(curLeft->_balance=-1)，最终cur的平衡因子为1，parent平衡因子为0，curLeft平衡因子为0
    3. curLeft本身是被插入节点(curLeft->_balanceFactor=0，H=0)，最终cur、parent、curRight平衡因子都为0
//parent->_balanceFactor == 2 && cur->_balanceFactor == -1
void rightLeftRotate(node* parent) //先右后左旋
{
    node* parent_RightChild = parent->_right; //parent_RightChild = cur
    node* parent_RightChild_LeftChild = parent_RightChild->_left; //parent_RightChild_LeftChild = curLeft
    int balanceFactor = parent_RightChild_LeftChild->_balanceFactor; 记录curLeft的平衡因子值：确定在b子树还是c子树插入

    rightSingleRotate(parent_RightChild); //右单旋cur为根的树
    leftSingleRotate(parent); //左单旋parent为根的树

    //更新cur、curRight、parent平衡因子（插入b，c子树不同位置会导致最终平衡因子的变化）
    if (balanceFactor == 1) //b子树插入
    {
        parent_RightChild->_balanceFactor = 0; //cur->_balanceFactor = 0
        parent->_balanceFactor = -1;
        parent_RightChild_LeftChild->_balanceFactor = 0; //curLeft->_balanceFactor = 0;
    }
    else if (balanceFactor == -1) //c子树插入
    {
        parent_RightChild->_balanceFactor = 1; //cur->_balanceFactor = 1
        parent->_balanceFactor = 0;
        parent_RightChild_LeftChild->_balanceFactor = 0; //curLeft->_balanceFactor = 0;
    }
    else if (balanceFactor == 0) //curLeft本身是被插入节点
    {
        parent_RightChild->_balanceFactor = 0; //cur->_balanceFactor = 0
        parent->_balanceFactor = 0;
        parent_RightChild_LeftChild->_balanceFactor = 0; //curLeft->_balanceFactor = 0;
    }
    else
    {
        assert(false);
    }
}

5. 检测

  1. 中序遍历是否升序
void inOrder() //中序遍历
{
    _inOrder(_root);
   	cout << endl;
}
void _inOrder(node* root) //中序遍历
{
 	if (root == nullptr)
    {
        return;
    }
    _inOrder(root->_left);
    cout << root->_couple.first << " ";
    _inOrder(root->_right);
}
  1. 是否平衡
bool isBalance() //判断树是否为平衡树
{
    return _isBalance(_root);
}
int heightDiffer(node* root)
{
    if (root == nullptr)
        return 0;
    int leftHeight = heightDiffer(root->_left);
    int rightHeight = heightDiffer(root->_right);

    return leftHeight > rightHeight ? leftHeight + 1 : rightHeight + 1; 
}

bool _isBalance(node* root) //判断树是否为平衡树(检查每个节点的左右子树高度差)
{
    if (root == nullptr)
        return true;

    int leftHeight = heightDiffer(root->_left);
    int rightHeight = heightDiffer(root->_right);
    if (rightHeight - leftHeight != root->_balanceFactor) //不只是对高度检查还应该对平衡因子检查
    {
        cout << "key:" << root->_couple.first << " node balanceFactor exception!" << endl;
        return false;
    }

    return abs(leftHeight - rightHeight) < 2 
        && _isBalance(root->_left) 
        && _isBalance(root->_right);
}

6. 完整代码

插入阶段

  1. 根节点为空
    1. new节点，改变根指向，返回true
  2. 根节点不为空
    1. 找到插入位置
      1. 右查找：当前节点key值 < 插入节点key值
      2. 左查找：当前节点key值 > 插入节点key值
      3. 当前节点key值 = 插入节点key值 ：直接返回false
    2. 在对应待插入位置插入
      1. new节点，当前插入位置指向该节点
      2. 右插入：当前节点key值 < 插入节点key值
      3. 左插入: 当前节点key值 > 插入节点key值
    3. 当前被插入节点父指针指向指向被连接节点
    4. 自动平衡
      1. 更新平衡因子
        1. 改变被插入节点父节点平衡因子
          1. 被插入节点在其父节点右子树中：父节点平衡因子+1
          2. 被插入节点在其父节点左子树中：父节点平衡因子-1
        2. 判断是否继续向上更新平衡因子
          1. 父节点平衡因子为1或者-1，继续更新
          2. 父节点平衡因子为0，无需更新
          3. 父节点平衡因子为2或者-2，子树不平衡，旋转处理使得平衡（旋转处理）
            1. parent->_balanceFactor == 2 && cur->_balanceFactor == 1 --> 左单旋
            2. parent->_balanceFactor == -2 && cur->_balanceFactor == -1 --> 右单旋
            3. parent->_balanceFactor == -2 && cur->_balanceFactor == 1 --> 先左后右旋
            4. parent->_balanceFactor == 2 && cur->_balanceFactor == -1 --> 先右后左旋
#pragma once
#include <iostream>
#include <utility>
#include <cassert>
using namespace std;

template <class KEY, class VAULE>
struct AVLtree_node
{
    AVLtree_node<KEY, VAULE>* _left; //左节点指向
    AVLtree_node<KEY, VAULE>* _right; //右节点指向
    AVLtree_node<KEY, VAULE>* _parent; //父节点指向

    pair<KEY, VAULE> _couple; //存储key/value
    int _balanceFactor; //平衡因子(左右子树高度差)

    AVLtree_node(const pair<KEY, VAULE>& couple)
        :_left(nullptr)
        ,_right(nullptr)
        ,_parent(nullptr)
        ,_couple(couple)
        ,_balanceFactor(0)
    {}
};

template <class KEY, class VAULE>
class AVLtree
{
    typedef AVLtree_node<KEY, VAULE> node;
public:
    bool insert(const pair<KEY, VAULE>& couple)
    {
        if (_root == nullptr) //根为空:直接new并指向返回
        {
            _root = new node(couple);
            return true;
        }

        /*找插入位置*/
        node* parent = nullptr; //起初根节点的父节点为nullptr
        node* cur = _root; //被插入节点指向
        while (cur)
        {
            if (cur->_couple.first < couple.first) //右查找：当前节点key值 < 插入节点key值
            {
                parent = cur;
                cur = cur->_right;
            }
            else if (cur->_couple.first > couple.first) //左查找: 当前节点key值 > 插入节点key值
            {
                parent = cur;
                cur = cur->_left;
            }
            else //当前节点key值 = 插入节点key值：直接退出
            {
                return false;
            }
        }

        /*在对应位置插入*/
        cur = new node(couple);
        if (parent->_couple.first > couple.first) //左插入: 当前节点key值 > 插入节点key值
        {
            parent->_left = cur;
        }
        else //右插入：当前节点key值 < 插入节点key值
        {
            parent->_right = cur;
        }
        cur->_parent = parent; //反向链接

        /*自动平衡 TODO*/

        //更新平衡因子
        while (parent)
        {
            if (cur == parent->_right) //被插入节点在其父节点右子树中
            {
                parent->_balanceFactor++;
            }
            else //被插入节点在其父节点左子树中
            {
                parent->_balanceFactor--;
            }

            if (parent->_balanceFactor == 1 || parent->_balanceFactor == -1) //继续更新平衡因子
            {
                parent = parent->_parent;
                cur = cur->_parent;
            }
            else if (parent->_balanceFactor == 0)
            {
                break;
            }
            else if (parent->_balanceFactor == 2 || parent->_balanceFactor == -2) //子树不平衡(旋转处理)
            {
                if (parent->_balanceFactor == 2 && cur->_balanceFactor == 1) //左单旋
                {
                    leftSingleRotate(parent);
                }
                else if (parent->_balanceFactor == -2 && cur->_balanceFactor == -1) //右单旋
                {
                    rightSingleRotate(parent);
                }
                else if (parent->_balanceFactor == -2 && cur->_balanceFactor == 1) //先左后右旋
                {
                    leftRightRotate(parent);
                }
                else if (parent->_balanceFactor == 2 && cur->_balanceFactor == -1) //先右后左旋
                {
                    rightLeftRotate(parent);
                }
                else
                {
                    assert(false);
                }

                //旋转可以达到左右子树平衡并且降低高度
                break;
            }
            else
            {
                assert(false);
            }
        }

        return true;
    }

    void inOrder() //中序遍历
    {
        _inOrder(_root);
        cout << endl;
    }

    bool isBalance() //判断树是否为平衡树
    {
        return _isBalance(_root);
    }

private:
    void leftSingleRotate(node* parent) //左单旋
    {
        //记录指针
        node* parent_RightChild = parent->_right; //parent_RightChild = cur
        node* parent_RightChild_LeftChild = parent_RightChild->_left; //parent_RightChild_LeftChild = curLeft
        node* parent_parent = parent->_parent; //局部根或整棵树根的父节点

        parent->_right = parent_RightChild_LeftChild; //让cur的左子树(curLeft)放在parent的右子树位置
        if (parent_RightChild_LeftChild != nullptr) //H为0时,parent_RightChild_LeftChild=nullptr
        {
            parent_RightChild_LeftChild->_parent = parent; //curLeft的父节点指向指向parent
        }
        parent_RightChild->_left = parent; //让parent放在cur的左子树位置
        parent->_parent = parent_RightChild; //parent的父节点指向指向cur
        
        //cur(parent_RightChild)变为子树或者整颗树的根
        if (parent_parent == nullptr) //parent是整颗树的根
        {
            _root = parent_RightChild; //cur(parent_RightChild)就是根
            _root->_parent = nullptr;
        }
        else //parent是局部子树的根
        {
            if (parent_parent->_left == parent) //parent节点在父节点的左子树位置
            {
                parent_parent->_left = parent_RightChild;
            }
            else //parent节点在父节点的右子树位置
            {
                parent_parent->_right = parent_RightChild;
            }
            parent_RightChild->_parent = parent_parent; //cur(parent_RightChild)指向局部根的父节点
        }

        //更新平衡因子
        parent->_balanceFactor = parent_RightChild->_balanceFactor = 0;
    }

    void rightSingleRotate(node* parent) //右单旋
    {
        //记录指针
        node* parent_LeftChild = parent->_left; //parent_LeftChild = cur
        node* parent_LeftChild_RightChild = parent_LeftChild->_right; //parent_LeftChild_RightChild = curRight
        node* parent_parent = parent->_parent; //局部根或整棵树根的父节点

        parent->_left = parent_LeftChild_RightChild; //让cur的右子树(curRight)放在parent的左子树位置
        if (parent_LeftChild_RightChild != nullptr)
        {
            parent_LeftChild_RightChild->_parent = parent; //让curRight父节点的指向指向parent
        }
        parent_LeftChild->_right = parent; //让parent放在cur的右子树位置
        parent->_parent = parent_LeftChild; //让parent的父节点指向指向cur

        //cur(parent_LeftChild)变为子树或者整颗树的根
        if (parent_parent == nullptr) //parent是整颗树的根
        {
            _root = parent_LeftChild; //cur(parent_LeftChild)就是根
            _root->_parent = nullptr;
        }
        else //parent是局部子树的根
        {
            if (parent_parent->_left == parent) //parent节点在父节点的左子树位置
            {
                parent_parent->_left = parent_LeftChild;
            }
            else //parent节点在父节点的右子树位置
            {
                parent_parent->_right = parent_LeftChild;
            }
            parent_LeftChild->_parent = parent_parent; //cur(parent_LeftChild)指向局部根的父节点
        }

        //更新平衡因子
        parent->_balanceFactor = parent_LeftChild->_balanceFactor = 0;
    }

    void leftRightRotate(node* parent) //先左后右旋
    {
        node* parent_LeftChild = parent->_left; //parent_LeftChild = cur
        node* parent_LeftChild_RightChild = parent_LeftChild->_right; //parent_LeftChild_RightChild = curRight
        int balanceFactor = parent_LeftChild_RightChild->_balanceFactor; //记录curRight的平衡因子值：确定在b子树还是c子树插入

        leftSingleRotate(parent->_left); //左单旋cur为根的树
        rightSingleRotate(parent); //右单旋parent为根的树

        //更新cur、curRight、parent平衡因子（插入b，c子树不同位置会导致最终平衡因子的变化）
        if (balanceFactor == 1) //c子树插入
        {
            parent->_balanceFactor = 0; 
            parent_LeftChild_RightChild = 0; //curRight->_balanceFactor = 0
            parent_LeftChild->_balanceFactor = -1; //cur->_balanceFactor = -1
        }
        else if (balanceFactor == -1) //b子树插入
        {
            parent->_balanceFactor = 1;
            parent_LeftChild_RightChild = 0; //curRight->_balanceFactor = 0
            parent_LeftChild->_balanceFactor = 0;  //cur->_balanceFactor = 0
        }
        else if (balanceFactor == 0) //curRight自身是被插入节点
        {
            parent->_balanceFactor = 0;
            parent_LeftChild_RightChild = 0; //curRight->_balanceFactor = 0
            parent_LeftChild->_balanceFactor = 0;  //cur->_balanceFactor = 0
        }
        else
        {
            assert(false);
        }
    }

    void rightLeftRotate(node* parent) //先右后左旋
    {
        node* parent_RightChild = parent->_right; //parent_RightChild = cur
        node* parent_RightChild_LeftChild = parent_RightChild->_left; //parent_RightChild_LeftChild = curLeft
        int balanceFactor = parent_RightChild_LeftChild->_balanceFactor; 记录curLeft的平衡因子值：确定在b子树还是c子树插入

        rightSingleRotate(parent_RightChild); //右单旋cur为根的树
        leftSingleRotate(parent); //左单旋parent为根的树

        //更新cur、curRight、parent平衡因子（插入b，c子树不同位置会导致最终平衡因子的变化）
        if (balanceFactor == 1) //b子树插入
        {
            parent_RightChild->_balanceFactor = 0; //cur->_balanceFactor = 0
            parent->_balanceFactor = -1;
            parent_RightChild_LeftChild->_balanceFactor = 0; //curLeft->_balanceFactor = 0;
        }
        else if (balanceFactor == -1) //c子树插入
        {
            parent_RightChild->_balanceFactor = 1; //cur->_balanceFactor = 1
            parent->_balanceFactor = 0; 
            parent_RightChild_LeftChild->_balanceFactor = 0; //curLeft->_balanceFactor = 0;
        }
        else if (balanceFactor == 0) //curLeft本身是被插入节点
        {
            parent_RightChild->_balanceFactor = 0; //cur->_balanceFactor = 0
            parent->_balanceFactor = 0;
            parent_RightChild_LeftChild->_balanceFactor = 0; //curLeft->_balanceFactor = 0;
        }
        else
        {
            assert(false);
        }
    }


    void _inOrder(node* root) //中序遍历
    {
        if (root == nullptr)
        {
            return;
        }
        _inOrder(root->_left);
        cout << root->_couple.first << " ";
        _inOrder(root->_right);
    }

    int heightDiffer(node* root)
    {
        if (root == nullptr)
            return 0;
        int leftHeight = heightDiffer(root->_left);
        int rightHeight = heightDiffer(root->_right);

        return leftHeight > rightHeight ? leftHeight + 1 : rightHeight + 1; 
    }

    bool _isBalance(node* root) //判断树是否为平衡树(检查每个节点的左右子树高度差)
    {
        if (root == nullptr)
            return true;

        int leftHeight = heightDiffer(root->_left);
        int rightHeight = heightDiffer(root->_right);
        if (rightHeight - leftHeight != root->_balanceFactor) //不只是对高度检查还应该对平衡因子检查
        {
            cout << "key:" << root->_couple.first << " node balanceFactor exception!" << endl;
            return false;
        }

        return abs(leftHeight - rightHeight) < 2 
            && _isBalance(root->_left) 
            && _isBalance(root->_right);
    }


private:
    node* _root = nullptr;
};


/*测试*/
void test_AVLtree1()
{
    //int arr[] = { 16, 3, 7, 11, 9, 26, 18, 14, 15 };
    int arr[] = { 4, 2, 6, 1, 3, 5, 15, 7, 16, 14};
    AVLtree<int, int> tree;
    for (auto x : arr)
    {
        tree.insert(make_pair(x, x));
    }

    tree.inOrder(); //中序遍历

    cout << tree.isBalance() << endl; //判断是否为平衡树

}

void test_perfermance() //测试性能
{
    srand(time(nullptr));
    const size_t N = 100000;
    AVLtree<int, int> tree;
    for (size_t i = 0; i < N; ++i)
    {
        size_t x = rand();
        tree.insert(make_pair(x, x));
    }

    cout << tree.isBalance() << endl; 

}

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/527634.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

Golang结构体入门

Golang结构体入门

目录 结构体基础 结构体示例 为结构体定义方法 组合结构体 嵌套结构体 指针结构体 匿名字段 面向对象 封装 继承 多态 结构体基础 1.结构体是值类型&#xff1a;在Go语言中&#xff0c;结构体是一种值类型&#xff0c;与数组和基本数据类型一样。当结构体被赋值给一…
阅读更多...
【MySQL】MySQL批量插入测试数据的几种方式

【MySQL】MySQL批量插入测试数据的几种方式

文章目录 前言一、表二、使用函数生成设置允许创建函数产生随机字符串产生随机数字 三、创建存储过程插入角色表插入用户表 四、执行存储过程小结五、使用 Navicat自带的数据生成 前言 在开发过程中我们不管是用来测试性能还是在生产环境中页面展示好看一点, 又或者学习验证某…
阅读更多...
企业为什么要数字化转型？

企业为什么要数字化转型？

数字化转型是使用数字技术从根本上改变企业运营方式并为客户创造价值的过程。企业进行数字化转型&#xff0c;常见因素包括&#xff1a; 提高效率&#xff1a;数字化转型可以简化流程并自动执行重复性任务&#xff0c;从而减少执行这些任务所需的时间和精力。可以节省成本并提高…
阅读更多...
网页三剑客之 Javascript

网页三剑客之 Javascript

JavaScript (简称 JS) 是世界上最流行的编程语言之一是一个脚本语言, 通过解释器运行主要在客户端(浏览器)上运行, 现在也可以基于 node.js 在服务器端运行 其实&#xff0c;语言都是触类旁通的&#xff0c;我们学过了C语言和JavaSE&#xff0c;那么学起其他任何语言都不难&a…
阅读更多...
CSS 中的常用属性(图文详解版)

CSS 中的常用属性(图文详解版)

CSS 中的常用属性 &#x1f50e;引入方式&#x1f50e;CSS 选择器&#x1f50e;字体&#x1f50e;文本&#x1f50e;背景&#x1f50e;圆角矩形&#x1f50e;元素的显示模式&#x1f50e;CSS 盒模型&#x1f50e;弹性布局&#x1f50e;结尾 CSS 中的属性有很多 本文列举了一些较…
阅读更多...
Spark大数据处理讲课笔记4.4 Spark SQL数据源 - JSON数据集

Spark大数据处理讲课笔记4.4 Spark SQL数据源 - JSON数据集

文章目录 零、本讲学习目标一、读取JSON文件概述二、读取JSON文件案例演示&#xff08;一&#xff09;创建JSON文件并上传到HDFS&#xff08;二&#xff09;读取JSON文件&#xff0c;创建临时表&#xff0c;进行关联查询1、读取user.json文件&#xff0c;创建临时表t_user2、读…
阅读更多...
Liunx下的进程信号

Liunx下的进程信号

文章目录 前言1.信号初识前置知识2.信号产生的方式1.键盘产生信号2.系统调用产生信号3.软件条件产生的信号4.硬件异常 3.信号的保存4.信号的处理1.用户态和内核态2.用户态和内核态的切换方式3.内核中信号的捕捉流程4.volatile关键字 前言 本文主要是对Liunx中进程信息进行讲解…
阅读更多...
Spark大数据处理讲课笔记4.5 Spark SQL数据源 - Hive表

Spark大数据处理讲课笔记4.5 Spark SQL数据源 - Hive表

文章目录 零、本讲学习目标一、Spark SQL支持读写Hive二、Spark配置hive-site.xml三、准备工作&#xff08;一&#xff09;启动Hive的metastore&#xff08;二&#xff09;启动Spark Shell 四、Spark读写Hive数据&#xff08;一&#xff09;导入SparkSession&#xff08;二&…
阅读更多...
Spark大数据处理讲课笔记4.8 Spark SQL典型案例

Spark大数据处理讲课笔记4.8 Spark SQL典型案例

文章目录 零、本讲学习目标一、使用Spark SQL实现词频统计&#xff08;一&#xff09;数据源 - words.txt&#xff08;二&#xff09;创建Maven项目&#xff08;三&#xff09;添加依赖和构建插件&#xff08;四&#xff09;修改源目录名称&#xff08;五&#xff09;创建日志属…
阅读更多...
Linux——线程2|线程控制

Linux——线程2|线程控制

什么是线程 在一个程序里的一个执行路线就叫做线程&#xff08;thread&#xff09;。更准确的定义是&#xff1a;线程是“一个进程内部的控制序列”。 一切进程至少都有一个执行线程 线程在进程内部运行&#xff0c;本质是在进程地址空间内运行 在Linux系统中&#xff0c;在CPU…
阅读更多...
基于Java+SpringBoot+vue+node.js的智能农场管理系统详细设计和实现

基于Java+SpringBoot+vue+node.js的智能农场管理系统详细设计和实现

基于JavaSpringBootvuenode.js的智能农场管理系统详细设计和实现 博主介绍&#xff1a;5年java开发经验&#xff0c;专注Java开发、定制、远程、指导等,csdn特邀作者、专注于Java技术领域 作者主页 超级帅帅吴 Java项目精品实战案例《500套》 欢迎点赞 收藏 ⭐留言 文末获取源码…
阅读更多...
报表设计器Stimulsoft 2023.2提供深色主题和 Monoline 图标包

报表设计器Stimulsoft 2023.2提供深色主题和 Monoline 图标包

Stimulsoft Reports 是一款报告编写器&#xff0c;主要用于在桌面和Web上从头开始创建任何复杂的报告。可以在大多数平台上轻松实现部署&#xff0c;如ASP.NET, WinForms, .NET Core, JavaScript, WPF, Angular, Blazor, PHP, Java等&#xff0c;在你的应用程序中嵌入报告设计器…
阅读更多...
【Vue】学习笔记-消息的订阅与发布

【Vue】学习笔记-消息的订阅与发布

消息的订阅与发布(基本不用) 消息订阅与发布(pubsub)消息订阅与发布是一种组件间的通信的方式&#xff0c;适用于任意组件间通信 消息订阅与发布 1.订阅消息∶消息名 2.发布消息︰消息内容 消息订阅与发布的工作流程&#xff1a; &#xff08;A是订阅者&#xff0c;B是发布…
阅读更多...
软件安全开发意识

软件安全开发意识

国务院印发的《“十四五”数字经济发展规划》中指出数字经济是继农业经济、工业经济之后的主要经济形态&#xff0c;是以数据资源为关键要素&#xff0c;以现代信息网络为主要载体&#xff0c;以信息通信技术融合应用、全要素数字化转型为重要推动力&#xff0c;促进公平与效率…
阅读更多...
MYSQL高可用配置（MHA）

MYSQL高可用配置（MHA）

1、什么是MHA MHA&#xff08;Master High Availability&#xff09;是一套优秀的MySQL高可用环境下故障切换和主从复制的软件。 MHA 的出现就是解决MySQL 单点的问题。 MySQL故障切换过程中&#xff0c;MHA能做到0-30秒内自动完成故障切换操作。 MHA能在故障切换的过程中最大…
阅读更多...
fastapi高性能异步框架，极速上手

fastapi高性能异步框架，极速上手

fastapi项目开发快速上手 简介 FastAPI 是一个用于构建 API 的现代、快速&#xff08;高性能&#xff09;的 web 框架&#xff0c;使用 Python 3.6 并基于标准的 Python 类型提示。 特性: 快速&#xff1a;可与 NodeJS 和 Go 比肩的极高性能&#xff08;归功于 Starlette 和…
阅读更多...
全流程各工程类型地下水环境影响评价【一级】方法与MODFLOW Flex建模

全流程各工程类型地下水环境影响评价【一级】方法与MODFLOW Flex建模

目录 专题一 地下水基础知识学习 专题二 地下水环境影响评价过程讲解 专题三 地下水数值软件的学习及操作 专题四 相关专业软件&#xff08;Surfer、Aquifer test&#xff09;的学习 专题五 化工类建设项目地下水环评关键技术处理及上机操作 专题六 化工类建设项目地下水…
阅读更多...
顶象助力如祺出行打造高品质服务

顶象助力如祺出行打造高品质服务

近日&#xff0c;广东省自然资源厅审批通过了如祺出行提交的测绘资质申请&#xff0c;如祺出行获得地理信息系统工程和互联网地图服务两个专业的乙级测绘资质。此次获批意味着&#xff0c;如祺出行能够在许可区域内依法合规开展数据标注和场景仿真等相关业务&#xff0c;构建全…
阅读更多...
Oracle11g全新讲解之触发器和视图索引

Oracle11g全新讲解之触发器和视图索引

触发器 1.触发器的基本讲解 当特定事件出现时自动执行的存储过程 语法结构 CREATE [OR REPLACE] TRIGGER trigger_name AFTER | BEFORE | INSTEAD OF [INSERT] [[OR] UPDATE [OF column_list]] [[OR] DELETE] ON table_or_view_name [REFERENCING {OLD [AS] old / NEW [AS]…
阅读更多...
探索Jetpack Compose的Material You主题

探索Jetpack Compose的Material You主题

探索Jetpack Compose的Material You主题 在本文中&#xff0c;我们将了解可用于 Jetpack Compose 的新 Material You 库&#xff0c;并了解我们如何将其动态颜色应用到 Stream Chat Compose SDK&#xff0c;以获得有趣、多彩和个性化的消息传递体验。 在本文中&#xff0c;您…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023