学习之前需要知道以下内容:
1. 递归
2. 二叉树
文章目录
- 线段树
- 介绍
- 用途
- 建树
- 修改
- 单点修改
- 区间修改
- 查询
- 代码实现。
- 建树
- 更新
- lazy传递
- 查询
- 练习
- 洛谷 P3372 【模板】线段树 1
- 题目描述
- 题解
线段树
介绍
线段树是一种二叉树,也可以归类为二叉搜索树。可以将区间的修改、维护和查询的时间复杂度优化为log级别的。
构成
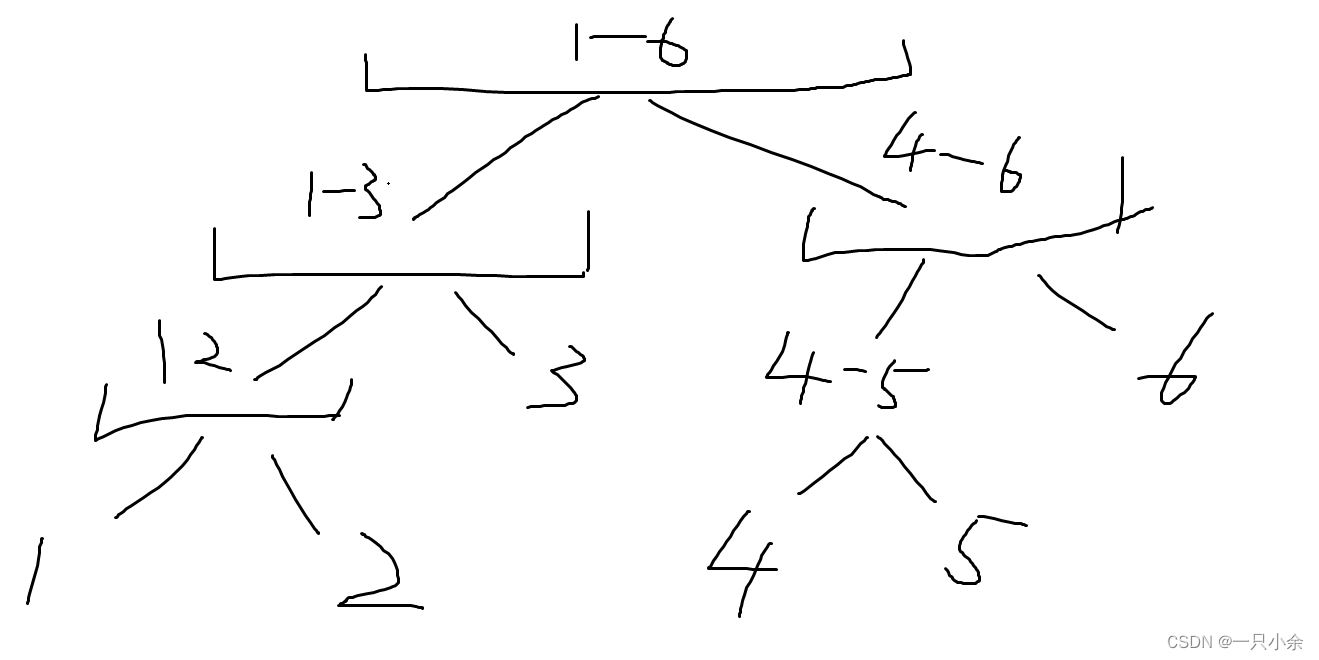
如一段1-6区间

可以分开为1-3和4-6然后继续放下拆分直到拆分为一个数的时候。
也就可以用树的标识。
用途
区间的加法
也可以结合 扫描线 用于二维面积并问题。
建树
存储方式我们使用数组来进行建树。这个要用到的就是二叉树的知识了。(对于 i i i 下标节点,左儿子下标为 2 ∗ i 2*i 2∗i,右儿子下标为 2 ∗ i + 1 2*i +1 2∗i+1 父节点下标为 i / / 2 i//2 i//2)
修改
单点修改
通过二叉树查询下标在进行修改。(二叉树查询为log级别)
然后更新大区间的值。

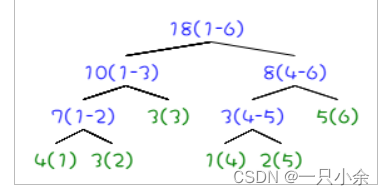
如修改下标2为数字3那么则需要更新为
区间修改
如将1-5的的值+2
则下面部分都需要+2
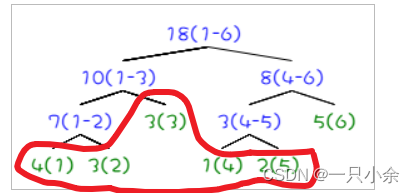
但是这样好像也没有啥优势,和数组一个个+2是一样的甚至,还多一些。
我们可以在这加一个缓存技术。
1-5就只需要更新这2个就可以了,然后在其lazy数组上设置为+2.
更新的值为长度*加的值
这里
10
10
10 就是
+
2
∗
3
+2*3
+2∗3 而
3
3
3 加上
2
∗
2
2*2
2∗2
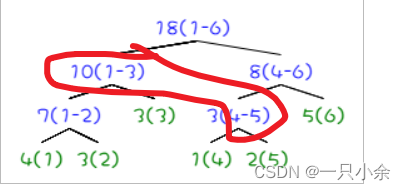
每次当要用到子节点的时候就需要将lazy标记下存了。
如现在
[
1
−
3
]
[1-3]
[1−3]的标记为
2
2
2 当我们要用到
[
1
]
[1]
[1]的时候
[
3
]
[3]
[3]就+2
[
1
−
2
]
[1-2]
[1−2]也+2
而
[
1
−
3
]
[1-3]
[1−3] 设置为0
然后继续递归
查询
这里和二叉树查询一样
不过需要注意的是。lazy标记下存的操作,在这里也是需要的。
如查询
[
1
−
2
]
[1-2]
[1−2]的值。
首先在
[
1
−
6
]
[1-6]
[1−6]的左,然后发现在
[
1
−
3
]
[1-3]
[1−3]的左,但是lazy为+2
所以
l
z
a
y
[
1
−
3
]
=
0
,
l
z
a
y
[
1
−
2
]
=
2
,
l
a
z
y
[
3
]
=
2
lzay[1-3] = 0,lzay[1-2]=2,lazy[3]=2
lzay[1−3]=0,lzay[1−2]=2,lazy[3]=2.
所以
[
1
−
2
]
=
l
z
a
y
[
1
−
2
]
+
[
1
−
2
]
=
2
+
7
=
9
[1-2] = lzay[1-2]+[1-2] = 2+7=9
[1−2]=lzay[1−2]+[1−2]=2+7=9
代码实现。
建树
使用递归来实现
/**
* 建树
* @param l 左边界
* @param r 右边界
* @param pos 当前位置
* @return 当前位置的值
*/
public long build(int l, int r, int pos) {
if (l == r) {
return tree[pos] = mapping[l - 1];
} else {
int mid = (l + r) >> 1;
return tree[pos] = build(l, mid, pos << 1)
+ build(mid + 1, r, pos << 1 | 1);
}
}
更新
每次从根节点开始进行。
如果查询和边界没有交点的时候停止递归

如果完全包括,那么就将这个区间更新。
更新规则:
- 区间值+value*长度
- 区间lazy +value

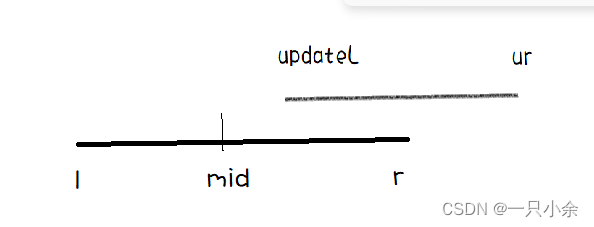
其他情况就是一部分在一部分不在,那么就进行向子节点查询
注意如果该节点lazy值不为空则需要向下传递。
向下查找完后,需要将子节点添加的值向本节点更新。
/**
* 更新
* @param l 左边界
* @param r 右边界
* @param pos 当前位置
* @param value 更新值
* @return 当前位置的值
*/
public long getUpdate(int l, int r, int pos, int value) {
if (r < updateL || l > updateR)
return 0;
if (l >= updateL && r <= updateR) {
lazy[pos] += value;
long v = (long) value * (r - l + 1);
tree[pos] += v;
return v;
} else {
int mid = (l + r) >> 1;
updateLazy(l, r, pos, mid);
long ul = getUpdate(l, mid, pos << 1, value);
long ur = getUpdate(mid + 1, r, pos << 1 | 1, value);
tree[pos] += ul + ur;
return ul + ur;
}
}
lazy传递
更新规则如下,
- 子节点的lazy设置为本节点的lazy
- 子节点数值更新
- 本节点lazy设置为0
/**
* 更新懒标记
* @param l 左边界
* @param r 右边界
* @param pos 当前位置
* @param mid 中间位置
*/
private void updateLazy(int l, int r, int pos, int mid) {
if (lazy[pos] != 0) {
lazy[pos << 1] += lazy[pos];
lazy[pos << 1 | 1] += lazy[pos];
tree[pos << 1] += lazy[pos] * (mid - l + 1);
tree[pos << 1 | 1] += lazy[pos] * (r - mid);
lazy[pos] = 0;
}
}
查询
这个没有太多好说的,和更新挺像的
一样需要注意的是lazy值的下移。
/**
* 查询
* @param l 左边界
* @param r 右边界
* @param pos 当前位置
* @return 当前位置的值
*/
public long getN(int l, int r, int pos) {
if (l > getR || r < getL)
return 0;
if (l >= getL && r <= getR) {
return tree[pos];
} else {
int mid = (l + r) >> 1;
int i = pos << 1;
int j = i | 1;
updateLazy(l,r,pos,mid);
return getN(l, mid, i) +
getN(mid + 1, r, j);
}
}
练习
洛谷 P3372 【模板】线段树 1
题目描述
如题,已知一个数列,你需要进行下面两种操作:
- 将某区间每一个数加上 k k k。
- 求出某区间每一个数的和。
输入格式
第一行包含两个整数 n , m n, m n,m,分别表示该数列数字的个数和操作的总个数。
第二行包含 n n n 个用空格分隔的整数,其中第 i i i 个数字表示数列第 i i i 项的初始值。
接下来 m m m 行每行包含 3 3 3 或 4 4 4 个整数,表示一个操作,具体如下:
1 x y k:将区间 [ x , y ] [x, y] [x,y] 内每个数加上 k k k。2 x y:输出区间 [ x , y ] [x, y] [x,y] 内每个数的和。
输出格式
输出包含若干行整数,即为所有操作 2 的结果。
样例 #1
样例输入 #1
5 5
1 5 4 2 3
2 2 4
1 2 3 2
2 3 4
1 1 5 1
2 1 4
样例输出 #1
11
8
20
提示
对于
30
%
30\%
30% 的数据:
n
≤
8
n \le 8
n≤8,
m
≤
10
m \le 10
m≤10。
对于
70
%
70\%
70% 的数据:
n
≤
10
3
n \le {10}^3
n≤103,
m
≤
10
4
m \le {10}^4
m≤104。
对于
100
%
100\%
100% 的数据:
1
≤
n
,
m
≤
10
5
1 \le n, m \le {10}^5
1≤n,m≤105。
保证任意时刻数列中所有元素的绝对值之和 ≤ 10 18 \le {10}^{18} ≤1018。
【样例解释】
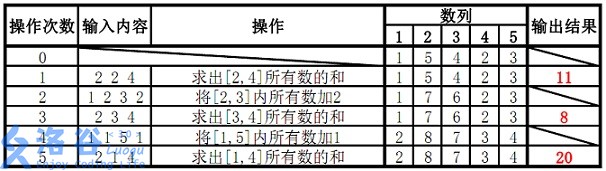
题解
import java.io.*;
public class Main {
static final StreamTokenizer st = new StreamTokenizer(new BufferedReader(new InputStreamReader(System.in)));
static final PrintWriter print = new PrintWriter(System.out);
public static int nextInt() throws IOException {
st.nextToken();
return (int) st.nval;
}
public static void main(String[] args) throws IOException {
int n = nextInt();
int m = nextInt();
int[] a = new int[n];
for (int i = 0; i < n; i++) {
a[i] = nextInt();
}
SegmentTrees s = new SegmentTrees(a);
for (int i = 0; i < m; i++) {
int j = nextInt();
if (j == 1) {
s.update(nextInt(), nextInt(), nextInt());
} else
print.println(s.get(nextInt(), nextInt()));
}
print.flush();
}
}
class SegmentTrees {
private final long[] tree;//线段树
private final int size;
private final int[] mapping;
private final long[] lazy;
public SegmentTrees(int[] mapping) {
this.size = mapping.length;
this.mapping = mapping;
this.tree = new long[size * 3 + 1];
this.lazy = new long[size * 3 + 1];
build(1, size, 1);
}
/**
* 建树
* @param l 左边界
* @param r 右边界
* @param pos 当前位置
* @return 当前位置的值
*/
public long build(int l, int r, int pos) {
if (l == r) {
return tree[pos] = mapping[l - 1];
} else {
int mid = (l + r) >> 1;
return tree[pos] = build(l, mid, pos << 1)
+ build(mid + 1, r, pos << 1 | 1);
}
}
public void update(int l, int r, int value) {
this.updateL = l;
this.updateR = r;
getUpdate(1, size, 1, value);
}
private int updateL;
private int updateR;
/**
* 更新
* @param l 左边界
* @param r 右边界
* @param pos 当前位置
* @param value 更新值
* @return 当前位置的值
*/
public long getUpdate(int l, int r, int pos, int value) {
if (r < updateL || l > updateR)
return 0;
if (l >= updateL && r <= updateR) {
lazy[pos] += value;
long v = (long) value * (r - l + 1);
tree[pos] += v;
return v;
} else {
int mid = (l + r) >> 1;
updateLazy(l, r, pos, mid);
long ul = getUpdate(l, mid, pos << 1, value);
long ur = getUpdate(mid + 1, r, pos << 1 | 1, value);
tree[pos] += ul + ur;
return ul + ur;
}
}
/**
* 更新懒标记
* @param l 左边界
* @param r 右边界
* @param pos 当前位置
* @param mid 中间位置
*/
private void updateLazy(int l, int r, int pos, int mid) {
if (lazy[pos] != 0) {
lazy[pos << 1] += lazy[pos];
lazy[pos << 1 | 1] += lazy[pos];
tree[pos << 1] += lazy[pos] * (mid - l + 1);
tree[pos << 1 | 1] += lazy[pos] * (r - mid);
lazy[pos] = 0;
}
}
public long get(int l, int r) {
this.getL = l;
this.getR = r;
return getN(1, size, 1);
}
private int getL;
private int getR;
/**
* 查询
* @param l 左边界
* @param r 右边界
* @param pos 当前位置
* @return 当前位置的值
*/
public long getN(int l, int r, int pos) {
if (l > getR || r < getL)
return 0;
if (l >= getL && r <= getR) {
return tree[pos];
} else {
int mid = (l + r) >> 1;
int i = pos << 1;
int j = i | 1;
updateLazy(l,r,pos,mid);
return getN(l, mid, i) +
getN(mid + 1, r, j);
}
}
}