参考资料:主动配电网网络分析与运行调控 (sciencereading.cn)
配电网重构是指在满足配电网运行基本约束的前提下,通过改变配电网中一个或多个开关的状态对配电网中一个或多个指标进行优化。通过配电网重构,可以在不增加设备投资的情况下,充分发挥配电系统的潜力,提高系统的性能指标,具有较好的经济效益。配电网重构的算法有许多,包括数学规划方法,如分支定界法、0-1 整数规划、单纯形法等;启发式算法,如最优流算法、开关交换法等;智能优化算法,如模拟退火算法、遗传算法、蚁群算法、粒子群算法、禁忌搜索算法等。这篇博客将采用混合整数二阶锥(Mixed-integer second-order cone programming, MISOCP)实现配电网重构问题的求解。
一、算例信息
以IEEE33节点测试系统作为算例,数据来源于matpower工具箱,数据文件如下:
function mpc = IEEE33
%% MATPOWER Case Format : Version 2
mpc.version = '2';
%%----- Power Flow Data -----%%
%% system MVA base
mpc.baseMVA = 10;
%% bus data
% bus_i type Pd Qd Gs Bs area Vm Va baseKV zone Vmax Vmin
mpc.bus = [ %% (Pd and Qd are specified in kW & kVAr here, converted to MW & MVAr below)
1 3 0 0 0 0 1 1 0 12.66 1 1 1;
2 1 100 60 0 0 1 1 0 12.66 1 1.1 0.9;
3 1 90 40 0 0 1 1 0 12.66 1 1.1 0.9;
4 1 120 80 0 0 1 1 0 12.66 1 1.1 0.9;
5 1 60 30 0 0 1 1 0 12.66 1 1.1 0.9;
6 1 60 20 0 0 1 1 0 12.66 1 1.1 0.9;
7 1 200 100 0 0 1 1 0 12.66 1 1.1 0.9;
8 1 200 100 0 0 1 1 0 12.66 1 1.1 0.9;
9 1 60 20 0 0 1 1 0 12.66 1 1.1 0.9;
10 1 60 20 0 0 1 1 0 12.66 1 1.1 0.9;
11 1 45 30 0 0 1 1 0 12.66 1 1.1 0.9;
12 1 60 35 0 0 1 1 0 12.66 1 1.1 0.9;
13 1 60 35 0 0 1 1 0 12.66 1 1.1 0.9;
14 1 120 80 0 0 1 1 0 12.66 1 1.1 0.9;
15 1 60 10 0 0 1 1 0 12.66 1 1.1 0.9;
16 1 60 20 0 0 1 1 0 12.66 1 1.1 0.9;
17 1 60 20 0 0 1 1 0 12.66 1 1.1 0.9;
18 1 90 40 0 0 1 1 0 12.66 1 1.1 0.9;
19 1 90 40 0 0 1 1 0 12.66 1 1.1 0.9;
20 1 90 40 0 0 1 1 0 12.66 1 1.1 0.9;
21 1 90 40 0 0 1 1 0 12.66 1 1.1 0.9;
22 1 90 40 0 0 1 1 0 12.66 1 1.1 0.9;
23 1 90 50 0 0 1 1 0 12.66 1 1.1 0.9;
24 1 420 200 0 0 1 1 0 12.66 1 1.1 0.9;
25 1 420 200 0 0 1 1 0 12.66 1 1.1 0.9;
26 1 60 25 0 0 1 1 0 12.66 1 1.1 0.9;
27 1 60 25 0 0 1 1 0 12.66 1 1.1 0.9;
28 1 60 20 0 0 1 1 0 12.66 1 1.1 0.9;
29 1 120 70 0 0 1 1 0 12.66 1 1.1 0.9;
30 1 200 600 0 0 1 1 0 12.66 1 1.1 0.9;
31 1 150 70 0 0 1 1 0 12.66 1 1.1 0.9;
32 1 210 100 0 0 1 1 0 12.66 1 1.1 0.9;
33 1 60 40 0 0 1 1 0 12.66 1 1.1 0.9;
];
%% generator data
% bus Pg Qg Qmax Qmin Vg mBase status Pmax Pmin Pc1 Pc2 Qc1min Qc1max Qc2min Qc2max ramp_agc ramp_10 ramp_30 ramp_q apf
mpc.gen = [
1 0 0 10 -10 1 100 1 10 0 0 0 0 0 0 0 0 0 0 0 0;
];
%% branch data
% fbus tbus r x b rateA rateB rateC ratio angle status angmin angmax
mpc.branch = [ %% (r and x specified in ohms here, converted to p.u. below)
1 2 0.0922 0.0470 0 0 0 0 0 0 1 -360 360;
2 3 0.4930 0.2511 0 0 0 0 0 0 1 -360 360;
3 4 0.3660 0.1864 0 0 0 0 0 0 1 -360 360;
4 5 0.3811 0.1941 0 0 0 0 0 0 1 -360 360;
5 6 0.8190 0.7070 0 0 0 0 0 0 1 -360 360;
6 7 0.1872 0.6188 0 0 0 0 0 0 1 -360 360;
7 8 0.7114 0.2351 0 0 0 0 0 0 1 -360 360;
8 9 1.0300 0.7400 0 0 0 0 0 0 1 -360 360;
9 10 1.0440 0.7400 0 0 0 0 0 0 1 -360 360;
10 11 0.1966 0.0650 0 0 0 0 0 0 1 -360 360;
11 12 0.3744 0.1238 0 0 0 0 0 0 1 -360 360;
12 13 1.4680 1.1550 0 0 0 0 0 0 1 -360 360;
13 14 0.5416 0.7129 0 0 0 0 0 0 1 -360 360;
14 15 0.5910 0.5260 0 0 0 0 0 0 1 -360 360;
15 16 0.7463 0.5450 0 0 0 0 0 0 1 -360 360;
16 17 1.2890 1.7210 0 0 0 0 0 0 1 -360 360;
17 18 0.7320 0.5740 0 0 0 0 0 0 1 -360 360;
2 19 0.1640 0.1565 0 0 0 0 0 0 1 -360 360;
19 20 1.5042 1.3554 0 0 0 0 0 0 1 -360 360;
20 21 0.4095 0.4784 0 0 0 0 0 0 1 -360 360;
21 22 0.7089 0.9373 0 0 0 0 0 0 1 -360 360;
3 23 0.4512 0.3083 0 0 0 0 0 0 1 -360 360;
23 24 0.8980 0.7091 0 0 0 0 0 0 1 -360 360;
24 25 0.8960 0.7011 0 0 0 0 0 0 1 -360 360;
6 26 0.2030 0.1034 0 0 0 0 0 0 1 -360 360;
26 27 0.2842 0.1447 0 0 0 0 0 0 1 -360 360;
27 28 1.0590 0.9337 0 0 0 0 0 0 1 -360 360;
28 29 0.8042 0.7006 0 0 0 0 0 0 1 -360 360;
29 30 0.5075 0.2585 0 0 0 0 0 0 1 -360 360;
30 31 0.9744 0.9630 0 0 0 0 0 0 1 -360 360;
31 32 0.3105 0.3619 0 0 0 0 0 0 1 -360 360;
32 33 0.3410 0.5302 0 0 0 0 0 0 1 -360 360;
21 8 2.0000 2.0000 0 0 0 0 0 0 0 -360 360;
9 15 2.0000 2.0000 0 0 0 0 0 0 0 -360 360;
12 22 2.0000 2.0000 0 0 0 0 0 0 0 -360 360;
18 33 0.5000 0.5000 0 0 0 0 0 0 0 -360 360;
25 29 0.5000 0.5000 0 0 0 0 0 0 0 -360 360;
];
%%----- OPF Data -----%%
%% generator cost data
% 1 startup shutdown n x1 y1 ... xn yn
% 2 startup shutdown n c(n-1) ... c0
mpc.gencost = [
2 0 0 3 0 20 0;
];
%% convert branch impedances from Ohms to p.u.
[PQ, PV, REF, NONE, BUS_I, BUS_TYPE, PD, QD, GS, BS, BUS_AREA, VM, ...
VA, BASE_KV, ZONE, VMAX, VMIN, LAM_P, LAM_Q, MU_VMAX, MU_VMIN] = idx_bus;
[F_BUS, T_BUS, BR_R, BR_X, BR_B, RATE_A, RATE_B, RATE_C, ...
TAP, SHIFT, BR_STATUS, PF, QF, PT, QT, MU_SF, MU_ST, ...
ANGMIN, ANGMAX, MU_ANGMIN, MU_ANGMAX] = idx_brch;
Vbase = mpc.bus(1, BASE_KV) * 1e3; %% in Volts
Sbase = mpc.baseMVA * 1e6; %% in VA
mpc.branch(:, [BR_R BR_X]) = mpc.branch(:, [BR_R BR_X]) / (Vbase^2 / Sbase);
%% convert loads from kW to MW
mpc.bus(:, [PD, QD]) = mpc.bus(:, [PD, QD]) / 1e3;二、基于yalmip构建数学模型
YALMIP是一个开源的 MATLAB工具箱,用于建模与求解优化问题,包括线性规划、混合整数线性规划、二次规划、半正定规划、凸优化等。该工具箱提供了高层次的优化接口,支持使用 MATLAB 的熟悉语法来描述优化问题,使得用户能够快速地尝试不同的建模和算法选择,从而便于对优化问题进行建模、求解和验证。此外,YALMIP工具箱还支持多种开源的优化求解器,包括 MOSEK、CPLEX、GLPK、SDPT3等,使得用户在对优化问题求解时具有多种选择。
使用yalmip工具箱求解优化问题的第一步就是需要定义决策变量,配电网重构问题中,决策变量包括支路状态,节点电压、支路有功/无功功率、电源有功/无功出力等。
首先需要设置系统相关的参数:
%% 系统参数
mpc0 = IEEE33;
nb=33; % 节点数
ns=1; % 电源节点数
nl=37; % 支路数
P_load=mpc0.bus(:,3)/mpc0.baseMVA; % 有功负荷
Q_load=mpc0.bus(:,4)/mpc0.baseMVA; % 无功负荷
r_ij=mpc0.branch(:,3); % 线路电阻
x_ij=mpc0.branch(:,4); % 线路电抗
M=1.06*1.06 - 0.94*0.94;
% 电源功率最大值
P_g_max=zeros(nb,1);
P_g_max(1)=10/mpc0.baseMVA;
Q_g_max=zeros(nb,1);
Q_g_max(1)=10/mpc0.baseMVA;
% 电源功率最小值
P_g_min=zeros(nb,1);
Q_g_min=[-10/mpc0.baseMVA;zeros(nb-1,1)];
% 支路功率最大值
Sij_max=15/mpc0.baseMVA;
% 最大电压
Vmax=[1;1.1*ones(32,1)];
Vmin=[1;0.9*ones(32,1)];
% 流入节点的支路
branch_to_node=zeros(nb,nl);
% 流出节点的支路
branch_from_node=zeros(nb,nl);
for k=1:nl
branch_to_node(mpc0.branch(k,2),k)=1;
branch_from_node(mpc0.branch(k,1),k)=1;
end随后需要定义决策变量:
%% 优化变量
z_ij=binvar(nl,1);% 支路开断情况
V_i=sdpvar(nb,1);% 节点电压
I_ij=sdpvar(nl,1);% 支路电流
P_ij=sdpvar(nl,1);% 线路有功功率
Q_ij=sdpvar(nl,1);% 线路无功功率
P_g=sdpvar(nb,1);% 电源有功出力
Q_g=sdpvar(nb,1);% 电源无功功率对于优化问题的约束条件,可以直接使用matlab语句添加到yalmip工具箱中,举个例子,如果我们要对一组变量x1, x2和x3进行优化,我们可能会需要满足以下两个约束条件:
1.x1 + x2 <= 10
2.2x2 + 3x3 >= 20
在yalmip中,我们可以使用 <= 或 >= 符号来表示这些限制条件,具体实现方法如下:
% 定义变量
x = sdpvar(3, 1);
% 定义约束条件
Constraints = [x(1) + x(2) <= 10, 2*x(2) + 3*x(3) >= 20];这样,我们就将这两个约束条件表达出来,并存放在Constraints变量中。在之后的优化求解中,yalmip会自动地考虑这些限制条件,并找到满足这些条件的最优解。
三、配电网重构基本原理
本博客将用数学规划的形式对网络重构问题进行描述,但由于严格的数学模型属于非线性非凸规划,理论上是一个NP难题而缺乏有效的求解方法。对此,可以根据需要引人二阶锥凸松弛技术和线性化方法,将原优化模型转化为具有凸可行域的形式以便求解。下面将针对网络重构问题,建立其对应的混合整数二阶锥规划模型。
1.1 目标函数
主动配电网进行网络重构的目标有多种,主要包括:降低网络有功损耗,降低系统一定时间段内能量损耗,使线路负载均衡,提高系统供电可靠性,以及提高电压稳定性等。假设目标函数选择为降低系统网络损耗:

使用matlab代码可表示为:
objective = sum(I_ij.^2*r_ij);或者:
objective =sum((P_ij.^2+Q_ij.^2)/V_i.^2.*r_ij);1.2拓扑约束
为了保护整定和减小短路电流,一般要求配电网呈辐射状运行,即网络中不存在环状拓扑结构。可以表示为:

Matlab代码表示为:
Constraints = [Constraints , sum(z_ij) == nb-ns];1.3电压安全约束

Matlab代码表示为:
Constraints = [Constraints, Vmin <= V_i,V_i <= Vmax];1.4 支路容量约束
配电网的每条线路都具有一定的传输容量,若实际传输电量过大,将使得电线发热量剧增,导致线路损耗增加且损伤输电线。线路容量可用视在功率的平方限值进行描述:

Matlab代码表示为:
Constraints = [Constraints, Sij_max'.^2.*z_ij >= P_ij.^2+Q_ij.^2];1.5 DistFlow潮流约束

对于网络重构而言,基本的 DistFlow潮流约束并不完善,仍存在以下三个问题需要解决。
(1)防止零注入孤立节点的存在。
零注入节点是指本身没有净流出或净注入功率的节点,即P_L和Q_L均为0。
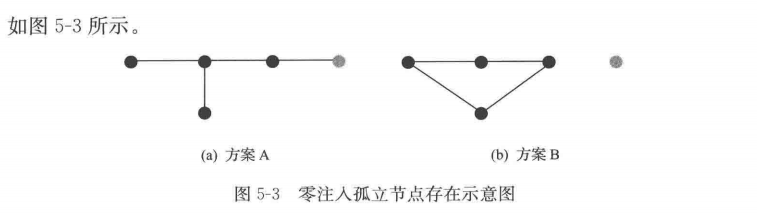
图中浅灰色节点表示零注入节点。重构方案A和B均满足辐射状约束式(5-38)和潮流约束,但方案B中却出现了孤立节点和环状结构并存的情况,显然不符合要求。为了防止这样的零注入孤立节点的存在,将式(5-42)和式(5-43)分别改进为

倘若支路ij处于断开状态,约束条件式(5-41)会将Pij和Qij限制为0,而此时式(5-44)将强制不相连支路两端的电压幅值相等,这是不合理的。对此,需要引入 big-M方法,将式(5-44)转变为如下形式:
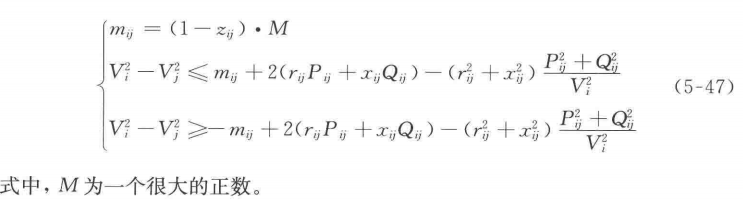
使用matlab代码表示为:
m_ij=(1-z_ij)*M;
Constraints = [Constraints, P_g-P_load+branch_to_node*P_ij-branch_to_node*(I_ij.*r_ij)-branch_from_node*P_ij == 0];
Constraints = [Constraints, Q_g-Q_load+branch_to_node*Q_ij-branch_to_node*(I_ij.*x_ij)-branch_from_node*Q_ij == 0];
Constraints = [Constraints,U_i(mpc0.branch(:,1))-U_i(mpc0.branch(:,2))<= m_ij + 2*r_ij.*P_ij + 2*x_ij.*Q_ij - ((r_ij.^2 + x_ij.^2)).*I_ij];
Constraints = [Constraints,U_i(mpc0.branch(:,1))-U_i(mpc0.branch(:,2))>= -m_ij + 2*r_ij.*P_ij + 2*x_ij.*Q_ij - ((r_ij.^2 + x_ij.^2)).*I_ij];
Constraints = [Constraints, U_i(mpc0.branch(:,1),:).*I_ij == P_ij.^2+Q_ij.^2];1.6 非凸约束的二阶锥松弛
由于式(5-45)、式(5-46)和式(5-47)的强非凸形式,该网络重构模型是一个非凸规划,属于NP难题而不易求解。为此,需要引入二阶锥松弛技术,将原模型转化为一个MISOCP问题。

在模型中添加式(5-48)和式(5-49)这两个新约束,用新变量替代原目标函数和约束条件中的对应项,并将支路容量约束式(5-41)用电流幅值约束式(5-50)替代:
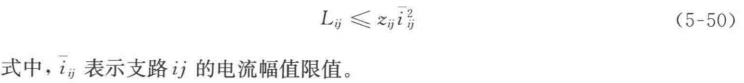
Matlab代码:
U_i=sdpvar(nb,1);% 电压的平方
L_ij=sdpvar(nl,1);% 电流的平方对于式(5-49)的非凸形式,在满足目标函数是L_ij的严格增函数及节点负荷无上界等条件下,可作如下变形:
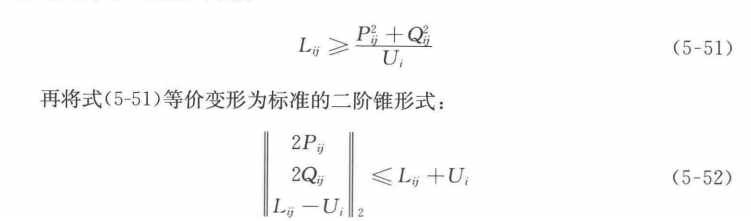
在yalmip中,标准二阶锥可以使用cone函数进行表示:
for k=1:nl
Constraints = [Constraints, cone([2*P_ij(k) 2*Q_ij(k) L_ij(k)-U_i(mpc0.branch(k,1))],L_ij(k)+U_i(mpc0.branch(k,1)))];
end最终,网络重构的MISOCP模型如下所示。
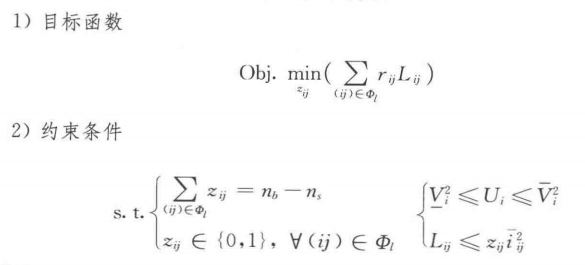
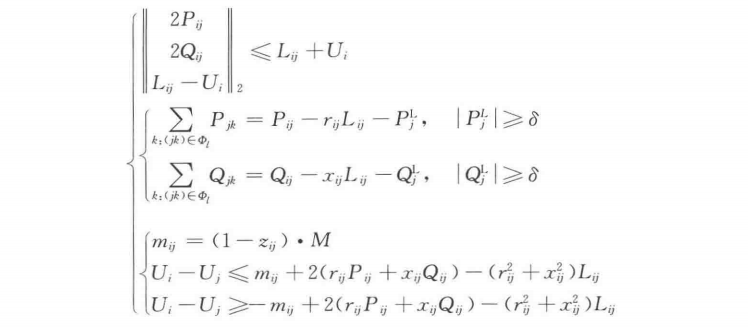
四、运行结果

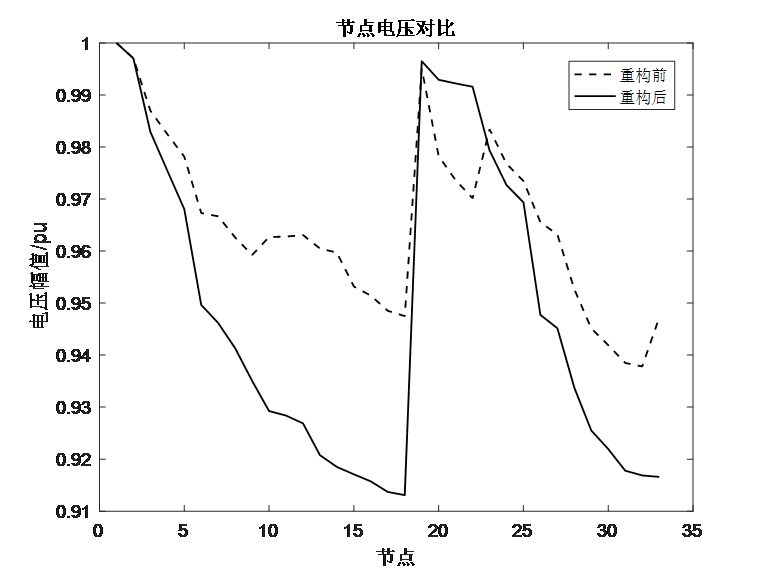
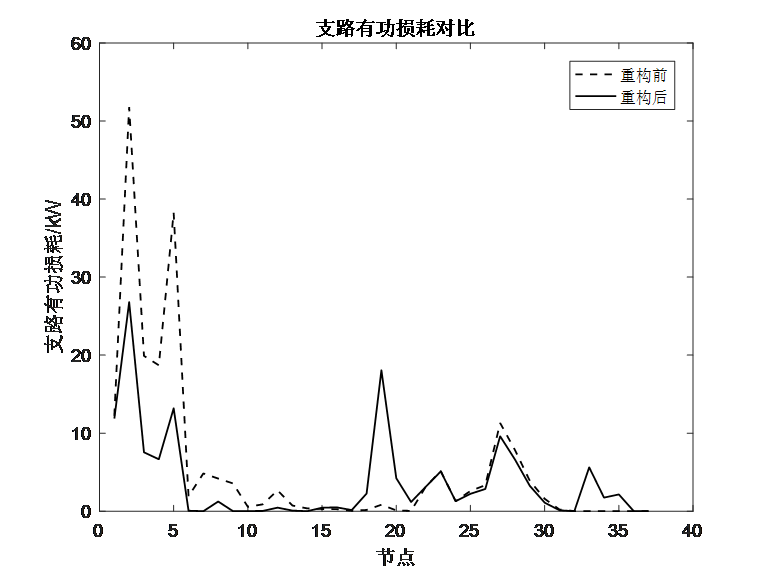
五、完整matlab代码
这个链接可以获取完整matlab代码:
基于混合整数二阶锥(MISOCP)的配电网重构的matlab代码