动态规划专题(1)
- 1.糖果(状压dp)
- 2.调手表(状压dp)
- 3.矩阵计数(状压dp)
- 4.蒙德里安的梦想(状压dp模板题)
- 5.跳跃(动态规划,搜索)
- 5.字符排序(逆序对(难))
- 6.子串分值和(哈希表+子串小推导)
- 7.游园安排(最长不上升子序列dp)
1.糖果(状压dp)
方法:状态压缩+简单dp(简称:状压dp)
状压dp方法步骤:
1.预处理好状态
2.使用处理好的状态进行dp
思路:对于每袋糖果,要么选,要么不选。对于当前选择的一袋糖果,如果
这袋糖果里面有之前没有尝过的,那么选择它,如果这袋糖果所有的口味都已经尝过,那么就不要这一袋。那么只需要将当前的尝过的口味的状态表示处理,就可以用简单的01背包去完成这道题。
#include <iostream>
#include<cstring>
#include<algorithm>
using namespace std;
const int N=(1<<20)+10,INF=0x3f3f3f3f;
int w[N]; //存放每一袋糖果的状态
int dp[N]; //dp[i]=j表示状态为i的情况下最少尝多少袋糖果
int n,m,k;
int main()
{
cin>>n>>m>>k; //袋数,口味种类,每袋的数量
memset(dp,-1,sizeof dp);
for(int i=1;i<=n;i++)
{
for(int j=0;j<k;j++)
{
int c;
cin>>c;
w[i]|=(1<<(c-1)); //运算符‘|’的规则是有1则1。
//解释一下这句话.
//1<<c表示1往左移动c-1个位置,表示第c位有糖果。
//然后利用‘|’运算符将这个位上的1添加到w[i]上面。
}
dp[w[i]]=1; //表示w[i]这个状态只需要1袋糖果就可以到达
}
dp[0]=0; //初始化dp,dp的第一步一定要初始化!!!初始化根据实际定义来。这里表示0种口味的状态的最少袋数,就是0
for(int i=1;i<=n;i++) //枚举袋数
{
for(int j=0;j<(1<<m);j++) //枚举状态
{
if(dp[j]!=-1) //如果当前状态存在,那么说明这个可以由这个状态去转移。
{
if((dp[j|w[i]])==-1) //选择第i袋糖果的状态没有存在,则说明找到了新口味,选它!
dp[j|w[i]]=dp[j]+1;
else //如果选了第i袋的状态和没有选i的状态是一样的。说明(j|w[i])这个状态的最小数之前算过了,那么比较一下选这一袋和之前的袋数哪个小
dp[j|w[i]]=min(dp[j]+1,dp[j|w[i]]);
}
else //否则这个状态一定是第第一次出现
{
continue;
}
}
}
cout<<dp[(1<<m)-1]<<endl;
return 0;
}
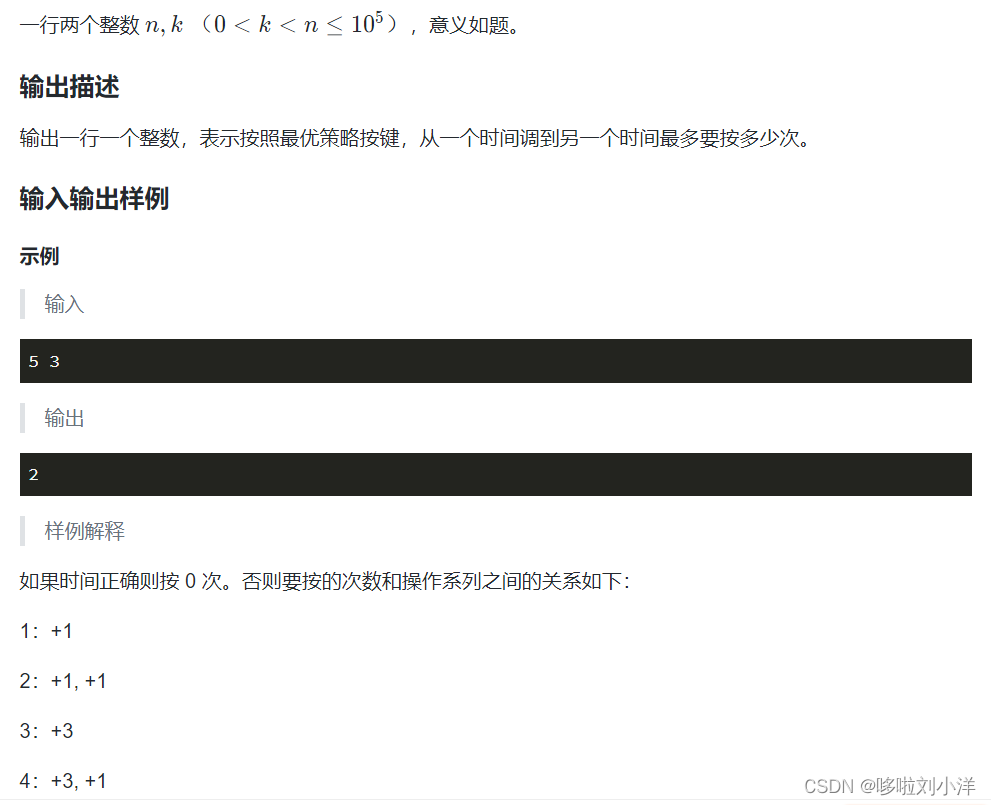
2.调手表(状压dp)
简单dp+预处理

#include<iostream>
#include<cstring>
#include<algorithm>
using namespace std;
const int N=100100;
int dp[N];
long long int n,k,j;
int main()
{
cin>>n>>k;
dp[0]=0;
for(int i=1;i<n;i++) //先算出调k不超过当前小时的情况
{
dp[i]=i;
if(i%k==0&&i>=k)dp[i]=i/k;
}
for(int i=1;i<n;i++) //考虑调k步的和之前的比较求出较小值
{
j=i*k%n;
dp[j]=min(dp[j],i);
}
for(int i=2;i<n;i++) //现在对于dp来说,每一个值要么只走k,要么走1和k,但是即走1又走k的情况只存在一个小时内,没有考虑完整
{
//要考虑是否走若干1,又调k绕圈到达某分钟步数最小
dp[i]=min(dp[i],min(dp[(i+n-k)%n],dp[i-1]))+1;
}
int res=0;
for(int i=1;i<n;i++)
res=max(res,dp[i]);
cout<<res<<endl;
return 0;
}
3.矩阵计数(状压dp)

思路:搜索或者状压dp
状压dp:(1)预处理合法状态。(2)定义dp。 (3)根据dp定义求状态转移方程
这道题的dp定义:dp[i][j][k]表示前i层,第i层的状态是j,第i-1层的状态是j-1的合法方案数
#include <iostream>
#include<cstring>
#include<algorithm>
#include<vector>
using namespace std;
const int N=1<<6;
vector<int>state; //存放合法状态
int dp[N][N][N]; //dp[i][j][k]表示前i层,第i层状态j,第i-1层状态时k的合理方案数量
int res=0;
int n,m;
bool check(int x) //挑选出合法状态
{
//不能有连续3个1
int sum=0; //记录1的个数
while(x)
{
if(x&1) //‘|‘:同1则1
{
sum++;
if(sum>=3)
return false;
}
else
sum=0;
x>>=1;
}
return true;
}
int main()
{
cin>>n>>m;
//预处理状态
//0表示0,1表示x
for(int i=0;i<1<<m;i++)
{
if(check(i))
state.push_back(i);
}
memset(dp,0,sizeof dp);
for(int i=0;i<state.size();i++) //初始化dp
dp[0][state[i]][0]=1; //表示第1层状态i时的方案,因为是第一层,所以只要该层的状态合法就行
for(int i=1;i<n;i++)
{
for(int j=0;j<state.size();j++) //第i层
for(int k=0;k<state.size();k++) //i-1层
for(int L=0;L<state.size();L++) //i-2层
{
if((state[j]&state[k]&state[L])==0) //表示合法状态
dp[i][state[j]][state[k]]+=dp[i-1][state[k]][state[L]];
}
}
int ans=0;
for(int i=0;i<state.size();i++)
for(int j=0;j<state.size();j++)
ans+=dp[n-1][state[i]][state[j]];
cout<<ans<<endl;
return 0;
}
用搜索来做
#include<iostream>
#include<cstring>
#include<algorithm>
#include<cmath>
using namespace std;
const int N=1<<6;
int v[N][N];
int n,m;
int ans=0;
bool check() //检查当前矩阵是否合法
{
for(int i=1;i<=n;i++)//考虑到可能每一行不足三个数
{
for(int j=1;j<=m;j++)
{
if(j+2<=m)
{
if(v[i][j]==1&&v[i][j+1]==1&&v[i][j+2]==1)
return false;
}
if(i+2<=n)
{
if(v[i][j]==1&&v[i+1][j]==1&&v[i+2][j]==1)
return false;
}
}
}
return true;
}
void dfs(int x,int y) //一个一个枚举
{
if(x==n&&y==m+1)
{
if(check())ans++;
return;
}
if(y==m+1) //说明该行已经枚举完,下一行
{
y=1; //从新的一行第一列开始
x++;
}
v[x][y]=0;
dfs(x,y+1);
v[x][y]=1;
dfs(x,y+1);
}
int main()
{
cin>>n>>m;
//用搜索来做
//一行一行来枚举
dfs(1,1); //从1行1列开始枚举
cout<<ans<<endl;
return 0;
//
}
4.蒙德里安的梦想(状压dp模板题)
5.跳跃(动态规划,搜索)


最基本的dp问题。递推即可。对于任意一格,有9种走法。实际上将题目简化一下就是对于任意一步只有两种走法。但是本质是一样的
#include <iostream>
#include<cstring>
#include<algorithm>
using namespace std;
const int N=110;
int w[N][N];
int dp[N][N]; //dp[i][j]表示当前位于(i,j)的位置上的总价值
int n,m;
int main()
{
cin>>n>>m;
for(int i=0;i<n;i++) //记录每一点的权值
for(int j=0;j<m;j++)
cin>>w[i][j];
//定义dp,推出dp方程
//dp[i][j]=max(以(i,j)为等腰三角形顶点,三角形内所有点都是前一步可能的点,注意这个等腰三角形和往前走的三角形是倒着的)
memset(dp,-0x3f,sizeof dp);
dp[0][0]=w[0][0];
for(int i=0;i<n;i++)
for(int j=0;j<m;j++)
{
//每一步都有9种走法
//往上走3个,往左走3个,斜着走3个
for(int a=1;a<=3;a++)
{
if(i>=a)
dp[i][j]=max(dp[i][j],dp[i-a][j]);
if(j>=a)
dp[i][j]=max(dp[i][j],dp[i][j-a]);
}
if(i>=1&&j>=1)
dp[i][j]=max(dp[i][j],dp[i-1][j-1]);
if(i>=1&&j>=2)
dp[i][j]=max(dp[i][j],dp[i-1][j-2]);
if(i>=2&&j>=1)
dp[i][j]=max(dp[i][j],dp[i-2][j-1]);
if(!(i==0&&j==0))
dp[i][j]+=w[i][j];
}
cout<<dp[n-1][m-1]<<endl;
return 0;
}
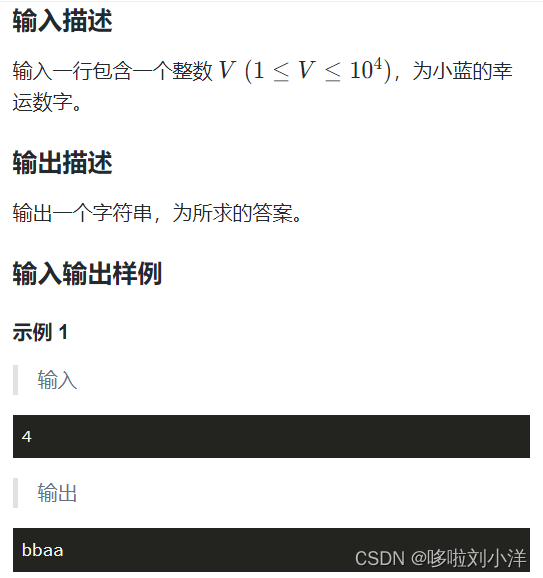
5.字符排序(逆序对(难))

#include<bits/stdc++.h>
using namespace std;
int V , len , now , cnt[27] , sum[27];
int get_max(int len){
return ((len - (len / 26 + 1)) * (len / 26 + 1) * (len % 26) + (26 - len % 26) * (len / 26) * (len - len / 26)) / 2;
}
bool check(int x , int n){//当前位置i放x字母后,后面的n个位置是否符合要求
memset(cnt , 0 , sizeof(cnt));//cnt记录后面n个位置放置的对应字符数量
int add1 = 0 , add2 = 0;
for(int j = 26 ; j >= x + 1 ; j --) add1 += sum[j];//1~i-1里边比当前插入字符大的字符数量
sum[x] ++ ;//当前字符数量增加1
for(int L = 1 ; L <= n ; L ++){//当前位置i放了x,看当前位置i后面剩下的n个位置能不能放好字母使得达到V的条件,这是一个预测过程
//ma保存i位置后面的n个位置能增加的最大逆序对个数 L-1-cnt[j]+num
//L-1-cnt[j]是当前字符之后的比当前字符小的字符数量的最大值
//num是1~pos+L-1前的比当前放置字符字典序大的字符数量
int ma = -1 , pos = 0 , num = 0;
for(int j = 26 ; j >= 1 ; j --){//枚举i位置后面的n个位置,每个位置放什么字母
if(L - 1 - cnt[j] + num > ma){//L - 1是算i+1到i+L的个数(不算i+L自己)
// - cnt[j] 如果在i+1到当前位置i+L前有放过字母j,然后当前位置i+L也尝试放j,
//那当前位置不和前面放j的位置构成逆序对 要减掉前面放j的位置个数
ma = L - 1 - cnt[j] + num;
pos = j;//在L这个位置放上字母j
}
num += sum[j];//num是从1-i位置里大于等于j的数的个数
//因为j是从26逆着放到1的 到下一轮循环时,j--假设记为j',那要求的1-i里比j'大的数就是num
//那么这个j'会和前面已经确定好的所有属于26~(j'+1)的数构成逆序对
//其实最后的num是算的所有大于等于1的个数,但是没关系,它不会更新到ma里
}
add2 += ma , cnt[pos] ++;//L这个位置确定下来,放pos这个字母
}
if(now + add1 + add2 >= V) {//now是i这个位置以前的所有逆序对个数,
//add1是i位置放进x后,x与前面所有字母构成的逆序对
//add2是i位置放进x后,后面的位置的所有数能增加的逆序对个数,分为2部分,
//1、后面位置所有的数与1~i部分的数构成的逆序对个数
//2、后面所有位置L,分别与从i+1~i+L-1之间的数构成的逆序对个数,然后这些逆序对的和
now += add1;//now更新i位置确定好放字母x后,从1~i位置所有逆序对个数
return true;
}
else {//i这个位置放x不能使逆序对个数>=V
sum[x] -- ;
return false;
}
}
signed main()
{
string ans = "";
cin >> V;
for(int i = 1 ; ; i ++) {
if(get_max(i) >= V){//i这个长度的字符串最多能有get_max(i)个逆序对 如果get_max(i) >= V,
//那么i这个长度就是我们需要的最短长度
len = i;
break ;
}
}
for(int i = 1 ; i <= len ; i ++){//按长度从左往右尝试放字母
for(int j = 1 ; j <= 26 ; j ++){//按顺序'a'-'z' 26个字母放 先用1-26代表这26个字母
if(check(j , len - i)){//现在是在第i位放j字母 看i后面的len-i个字母能否符合条件
ans += char(j + 'a' - 1);//符合条件就把j放在i这个位置
break ;//然后尝试放下一个位置
}
}
}
cout << ans << '\n';
return 0;
}
6.子串分值和(哈希表+子串小推导)

思路:
原始思路是枚举所有的子串,然后对每个子串进行求值,最后求和。但是这样会超时。
换个方法:枚举所有字符,累加另包含当前字符的子串数目。
#include <iostream>
#include<cstring>
#include<algorithm>
#include<cstdio>
using namespace std;
const int N = 1e6 + 10,INF=0x3f3f3f3f;
int visited[1000];
long long int sum = 0;
int main()
{
string s;
cin >> s;
memset(visited, -INF, sizeof visited);
//我们要算出每个字母的贡献值累加即可
//(1)当前字母如果在前面出现过,那么以最近一次出现该字母后面的一个字母为起点,字符串最后一格字符为终点。当前字母将
//起点到终点分为两个部分,两个部分相乘即可
for (int i = 0; i < s.length(); i++)
{
//枚举到当前字符,以当前字符为中心将字符串分为两个部分
long long int L, R; //L表示左边的字符个数,R右边.左右相乘
if (visited[s[i]] <0) //说明该字符前面没有出现过。
{
L = i + 1;
R = s.length() - i;
}
else //否则出先过,应该从最近一次出现的后一个字符作为起始字符
{
L = i - visited[s[i]];
R = s.length() - i;
}
sum += L * R; //左右相乘
visited[s[i]] = i; //更新当前字符的位置
}
cout << sum << endl;
return 0;
}
7.游园安排(最长不上升子序列dp)


#include <iostream>
#include<cstring>
#include<algorithm>
using namespace std;
const int N = 1e5 + 10;
int dp[N]; //dp[i]=j表示
string s[N]; //s[1]表示第一个名字
int path[N]; //存放路径
int a[N]; //存放路径
int main()
{
string str;
cin >> str;
int k = -1;
for (int i = 0; i < str.length(); i++) //预处理字符串 ,先预处理一下名字,将其放入一个string数组
{
if (str[i] >= 'A' && str[i] <= 'Z')
{
k = k + 1;
s[k]+=str[i];
}
else
s[k]+=str[i];
}
//初始化dp
for (int i = 0; i <= k; i++) //k个名字
dp[i] = 1;
memset(path, -1, sizeof path);
memset(a, -1, sizeof a);
int start = 0;
int res = 0;
for (int i = 0; i <= k; i++)
{
string temp="";
for (int j = 0; j < i; j++)
{
if (s[i]>s[j]) //要严格满足s[i]>s[j]才行
{
if (dp[j] + 1 > dp[i])
{
dp[i] = dp[j] + 1;
path[i] = j;
temp = s[j]; //将最新的s[j]保存
}
else
if (dp[j] + 1 == dp[i]) //如果等于,取最小的s[j]
{
if (temp>s[j]) //如果temp>s[j],说明temp比当前的s[j]大,我们要取小的
{
path[i] = j;
temp = s[j];
}
}
}
}
if (dp[i] > res)
{
res = dp[i];
start = i;
}
else
if (dp[i] == res) // 可能有相同长度的子序列,需要挑选出字典序最小的
{
if(s[start]>s[i]) //如果之前的最小字典序的子序列大于等于当前的子序列,我们优先选择小的
start = i;
}
}
int i = 0;
while (start != -1)
{
a[i++] = start;
start = path[start];
}
for (i = res - 1; i >= 0; i--)
cout<<s[a[i]];
return 0;
}