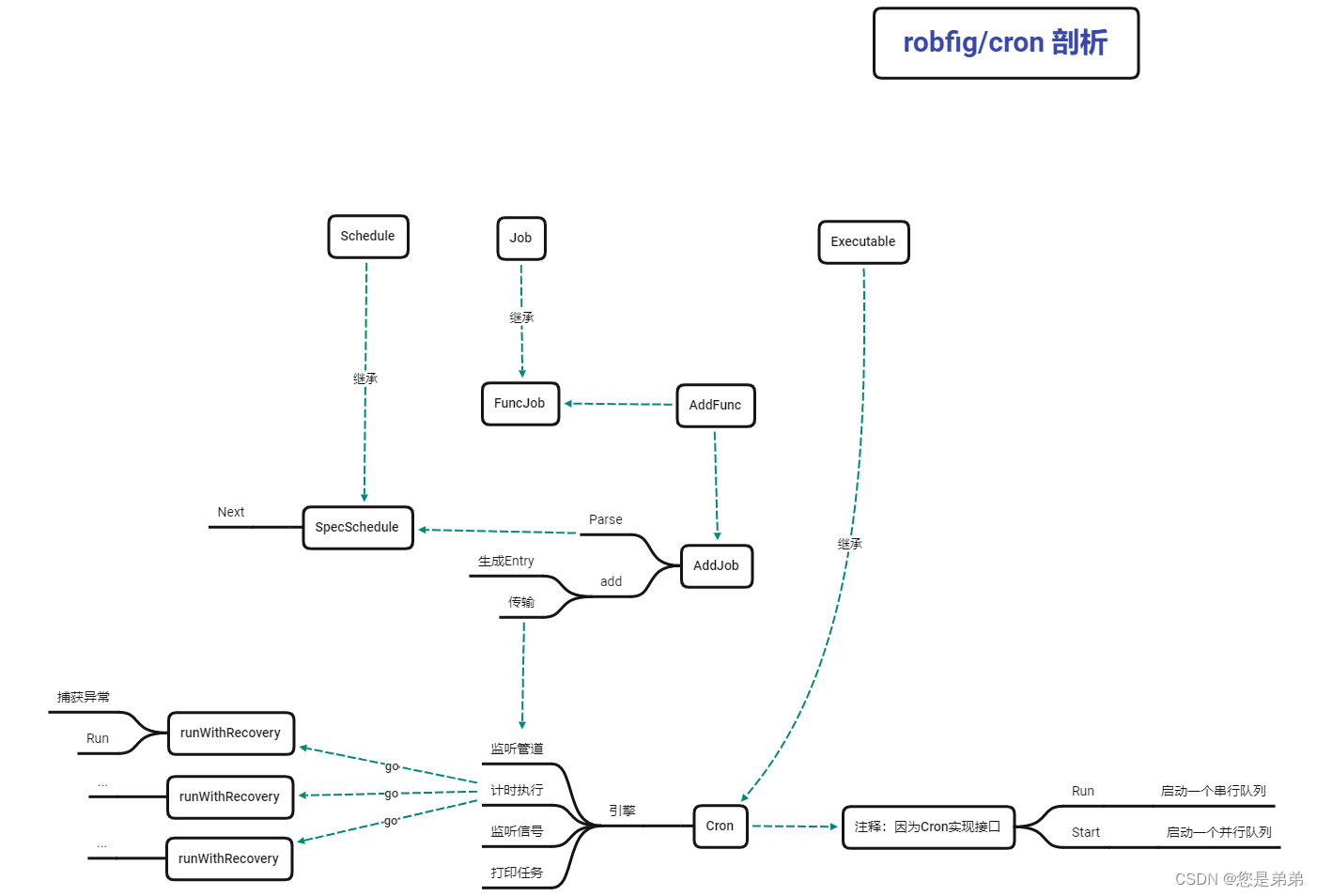
7.1.概述
平衡二叉树是要求任意结点的左右子树高度差不超过1,因此在AVL中用旋转来保证树的绝对平衡,但是这些旋转操作步骤繁多很耗时间,所以在面对经常会有数据插入的场景时,AVL不是一个性能优秀的选择。这时候反过来思考一个问题,旋转是为了保证树的绝对平衡,但是树的绝对平衡是必须的吗?显然不是,树的高度差只要不是太高从而退化成斜二叉树其实就能接受。
红黑树就是一种不严格平衡的,实现平很二叉树思想的二叉树,其通过对结点的染色+少量的旋转操作来保证树的相对平衡,保证树的高度差不会太高,提升了树在数据插入时的效率。
红黑树需要满足以下性质:
- 整棵树上单个结点的颜色,要么是红色,要么是黑色。
- 根节点必须为黑色。
- 父子不能同为红色。
- 从任何节点出发,到达叶节点经过的黑色节点数量一致。
7.2.操作
7.2.1.插入
插入技巧总结为:
根节点必为黑色,任何调整动作都无法将根节点染红
- 新插入节点的父节点和uncle节点同为红色,直接染黑父节点和uncle节点,染红祖父节点(如果祖父节点为根节点,就免疫)。
- 新插入节点的父节点为红色,uncle节点为空或者黑色分以下两种情况处理:
- 连续红节点同侧(即父节点如果在树的右子树,子节点也是父节点的右节点),以父节点为基准,左旋。
- 连续红节点异侧,先将祖父节点、父节点变色,然后以祖父节点为基准右旋。
- 旋转动作后变为叶子节点的节点染红,变为根节点的节点染黑。
(图盗自之前自己的上一个ID的博客,偷个懒了,不想画了,哈哈哈哈~~~)

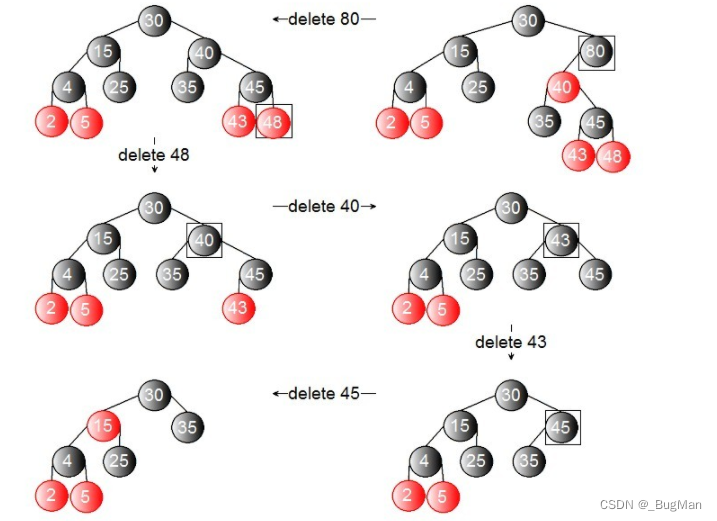
7.2.2.删除
1.概述
红黑树的删除其实就是基于二叉搜索树的删除上加入一个调色过程。
在弄清楚红黑树的删除操作之前,需要明白二叉搜索树的删除方法。
首先要明白几个概念:
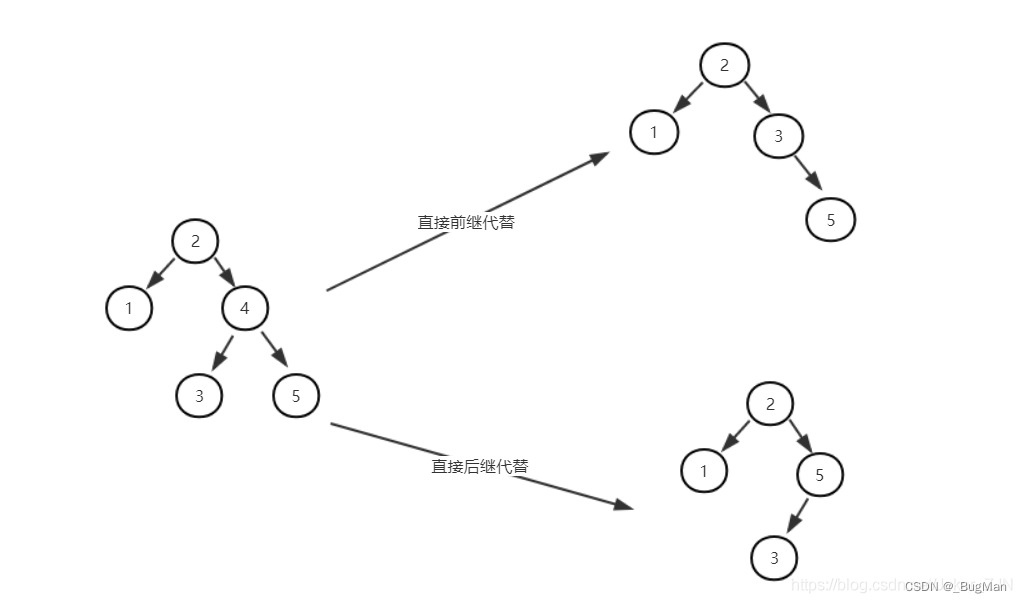
- 直接前继
- 直接后继
直接前继:
当前节点左子树的最右节点。此节点是当前节点左子树中的最大值,也就是左子树区间中值最接近当前节点的节点。
直接后继:
当前节点右子树的最左节点。此节点是当前节点右子树中的最小值,也就是右子树区间中值最接近当前节点的节点。
所以,二叉搜索树的删除思路就是用所要删除的直接前继或者直接后继节点来代替该节点即可。这样整颗二叉搜索树仍然会保持有序。
2.删除过程
删除技巧总结为:
- 当被删除元素为红时,直接删除。
- 当被删除元素为黑且为根节点时,直接删除。
- 当被删除元素为黑,且有一个右子节点为红时,将右子节点涂黑放到被删除元素的位置。
- 当被删除元素为黑,且兄弟节点为黑,兄弟节点两个孩子也为黑,父节点为红,此时,交换兄弟节点与父节点的颜色;NIL元素是指每个叶节点都有两个空的,颜色为黑的NIL元素,需要他的时候就可以把它看成两个黑元素,不需要的时候可以忽视他。
- 当被删除元素为黑、并且为父节点的左支,且兄弟颜色为黑,兄弟的右支为红色,这个时候需要交换兄弟与父亲的颜色,并把父亲涂黑、兄弟的右支涂黑,并以父节点为中心左转。
- 当被删除元素为黑、并且为父节点的左支,且兄弟颜色为黑,兄弟的左支为红色,这个时候需要先把兄弟与兄弟的左子节点颜色互换,进行右转,然后就变成了规则5一样了,在按照规则5进行旋转。
- 当被删除元素为黑且为父元素的右支时,跟情况5.情况6 互为镜像。
- 被删除元素为黑且兄弟节点为黑,兄弟节点的孩子为黑,父亲为黑,这个时候需要将兄弟节点变为红,再把父亲看做那个被删除的元素(只是看做,实际上不删除),看看父亲符和哪一条删除规则。