本篇文章是我在2022年阅读完distill上一篇文章"A Gentle Introduction to Graph Neural Networks"后自己的一些心得。

目录

一、不同类型的数据如何以图的形式保存

二、图结构可以处理的问题

三、图机器学习的挑战

四、图神经网络

一、不同类型的数据如何以图的形式保存

1. 用图来表示图像

​ 图像是具有色彩通道的矩形网格，它通常由长、宽以及色彩通道数三部分组成。图像也可以看作是一个规则的图，其中每个像素点(pixel)表示为一个节点，每个节点有一个3维的向量来表示该像素点的RGB像素值。另外，如下图所示，每个节点与它相邻的节点之间有一条边相连，每个非边界的节点都有8个节点来与其相连。

2.用图来表示文本

​ 我们可以将文本以每个字符、每个单词的形式划分为多个切片，然后用多个切片作为一个序列来表示文本。因此可以用有向图来表示这个文本，每一个切片作为一个节点，并且在它与它后面的一个节点连接一条有向边。下图所示为一段文本以图表示的邻接矩阵。

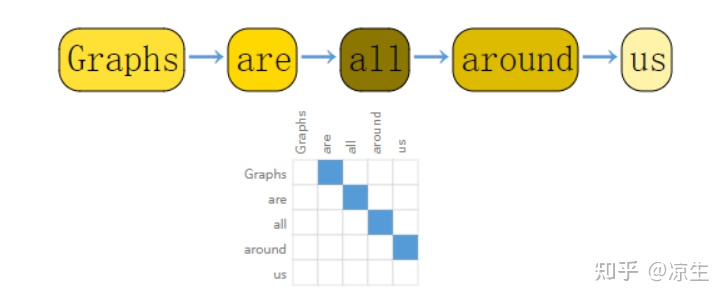
当然，以这种方式来表示图和文本具有很大的冗余性，比如图的邻接矩阵是一个对称矩阵，而文本的矩阵每个节点至多只有一条有向边连接到它和一条边由它连出。而且我认为图神经网络目前最大的用处还是用来处理图数据，对于cv和nlp领域只能说是可以处理，但是处理效果还不是很好。

3.用图来表示分子和社交网络

图很适合用来表示分子和社交网络，因为分子以及社交网络，他们都具有大小不固定，邻居数量不固定等特点。借助图来表示分子和社交网络，我们可以利用处理这些图来进行一些分子的毒性预测、人物社交关系预测等任务。下图是分子和社交网络用图表示的两个例子。

二、图结构可以处理的问题

1. 图水平的任务(Graph-level task)

​ 在图水平的任务中，我们的目标是预测一张完整的图。在上文已经提到过，一个分子可以用一张图来表示，我们可以通过分子的图结构来预测分子的气味，或者是否能与疾病中的受体相结合。

2.节点水平的任务(Node-level task)

​ 在节点水平的任务中，我们的任务是预测图中的某些节点。一个经典的节点预测问题是扎克的空手道俱乐部。这个数据集是一个单一的社交网络，其中每个节点表示单个的空手道练习者，边表示他们之间相互认识并且有互动。在某一天Hi教练和John管理员发生了分歧，所有的空手道练习者需要选择支持的一方。这个预测问题就是分类每一个节点，也就是空手道练习者会支持教练或者管理员的哪一方，这个就与节点到教练和管理员之间的边联系程度高度相关。

3.边水平的任务(Edge-level task)

​ 在边水平的任务中，我们的任务是预测边的属性。其中一个例子就是图像场景预测。在图像中，节点用来表示图像中的每一个对象，例如不同的人或动物等。我们希望预测这些节点对中边的值为多少来表示对象与对象之间的关系，如下图所示。

三、图机器学习的挑战

1.很难表示图的连通性

​ 图中的连通性很难表示，一个直观的想法是用邻接矩阵来表示图的连通性，但是这应用到机器学习中是不现实的，因为在数据集中，每一个图的节点数量不是固定的，也就是说每个数据的邻接矩阵大小不定。除此之外，在大型的图网络中，节点数量可能有几百万甚至几千万，这就导致图的邻接矩阵非常大，根本无法直接扔到网络中去进行运算。

2.节点的置换不变性

​ 对于图像来说，每一个像素的位置是确定的。而图中的节点并没有顺序一说，因此许多不同的邻接矩阵具有相同的连通性，他们可以表示为同一张图，这些邻接矩阵进入图神经网络后应该有相同的表示，其中一个例子如下所示，下面的邻接矩阵都表示上面同一个图。

四、图神经网络(GNN)

​ 图的描述是一种以排列不变的矩阵格式，因此GNN要保留图的对称性(排列不变性)来对图的所有属性(节点、边、全局上下文)来进行可优化变换。GNN采用了图输入、图输出的方式，将信息存储在节点、边或全局上下文中，通过改变这些信息的嵌入来进行一些相关的操作。

1.简单的GNN

最简单的图神经网络首先是将节点、边和全局表示为一个向量(图嵌入)，然后在每一个维度都使用单独的多层感知器(MLP)来进行训练，从而更新每一个属性的嵌入，如下图所示。

2.利用简单的GNN进行预测

二分类情况

​ 如果只是对节点进行二分类任务，并且图中每一个节点都有对应的信息，那很容易可以对于每一个节点的嵌入应用线性分类器进行分类，如下图所示。

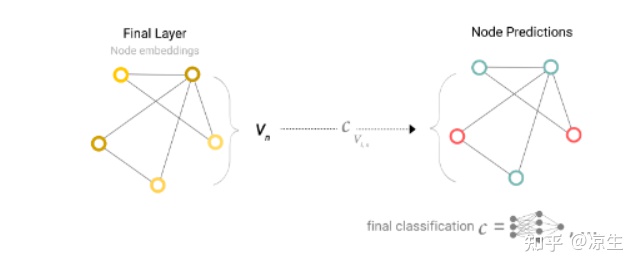
​ 但是有时候信息可能存储在边中，但仍要对节点进行划分，这时候就需要将边的信息收集提供给节点，一个简单的方法是用一个求和运算来聚集边的信息，对于每一个节点，将其连接的边的信息以及本身的信息进行求和，从而作为节点的表示。

​ 如果我们只有节点特征，但是需要对全局属性进行分类，那么我们可以将所有节点的属性收集在一起并进行聚合，这一步类似于CNN的全局平均池化层。

​ 在这个简单的GNN中，我们对于每一个属性都是独立处理的，并没有利用图的连通性，只有在汇集信息进行预测的时候才使用了连通性

3.添加全局表达

​ 到目前为止所描述的网络有一个缺陷，即使我们有多次应用消息传递，图中彼此远离的节点可能永远都无法互相传递信息，对于一个节点，如果有k层，那么消息最多传递K步。这种问题的一个解决方法是使用图的全局表示(U)，它是由一个图嵌入向量组成，它连接到网络中的所有其他节点和边，可以充当他们之间传递信息的桥梁，每次更新节点属性时，将全局信息也聚集到节点属性中进行更新，就可以获得更好的效果，如下图所示。

4.图神经网络参数的影响

​ 上图横坐标表示参数个数，纵坐标表示测试精度，可以看到，随着参数的增多，测试精度也在整体增高。但与此同时也可以看到，即使拥有少量的参数，也可以找到一个具有高性能的模型，这取决于不同图属性进行图嵌入时的图维度选择。

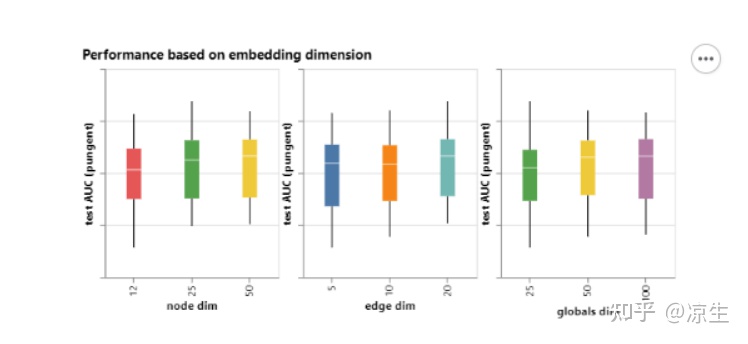
​ 我们可以注意到，具有较高维度的模型往往具有更好的平均值和下限性能，但对于最大值没有发现相同的趋势。一些性能最好的模型可以用于较小的尺寸。由于更高的维度也将涉及更多的参数，因此这些观察结果与前面的数字一致。

5.图采样

​ 训练神经网络常用的一种方法就是将训练数据划分为多个小批量，进行批量梯度更新。由于彼此相邻的节点和边的数量变化，这一实践对图形提出了挑战，这意味着我们不能拥有恒定的批量大小。

​ 如何对图表进行采样是一个开放的研究问题。如果我们关心在邻域级别上保留结构，一种方法是随机抽取统一数量的节点，即我们的节点集。然后添加与节点集相邻的距离为k的相邻节点，包括它们的边。每个邻域可以被认为是一个单独的图，GNN可以在这些子图的批次上训练。由于所有相邻节点都有不完整的邻域，因此可以屏蔽损失以仅考虑节点集。一种更有效的策略可能是首先随机采样单个节点，将其邻域扩展到距离k，然后在扩展集中选择另一个节点。一旦构建了一定数量的节点、边或子图，这些操作就可以终止。如果上下文允许，我们可以通过选择一个初始节点集，然后对恒定数量的节点进行子采样（例如，随机或通过随机漫游或Metropolis算法）来构建恒定大小的邻域。