1. 原理介绍

并查集是一种用于维护集合关系的数据结构，它支持合并集合和查询元素所在的集合。它的基本思想是将元素分组，每个组称为一个集合，最终目的是实现高效地判断两个元素是否在同一集合中。并查集维护的是一棵树，其中每个节点代表一个元素，节点之间的边表示它们属于同一个集合。初始时，每个元素都是一个独立的集合，也就是一棵只有一个节点的树。合并两个集合时，只需要将其中一个集合的根节点挂在另一个集合的根节点下面即可。查询元素所在的集合时，只需要一直向上找到根节点即可。并查集的时间复杂度取决于路径压缩和按秩合并这两种优化策略。路径压缩是指在查询根节点的过程中，将路径上的所有节点都直接挂在根节点下面，以减少下次查询的时间。按秩合并是指在合并两个集合的时候，将元素个数少的集合挂在元素个数多的集合下面，以保持树的平衡性。

2. 并查集的应用

并查集常用于解决图论中的连通性问题，例如判断无向图是否连通，求图的最小生成树等。另外，它还可以用于离散化处理等场景。

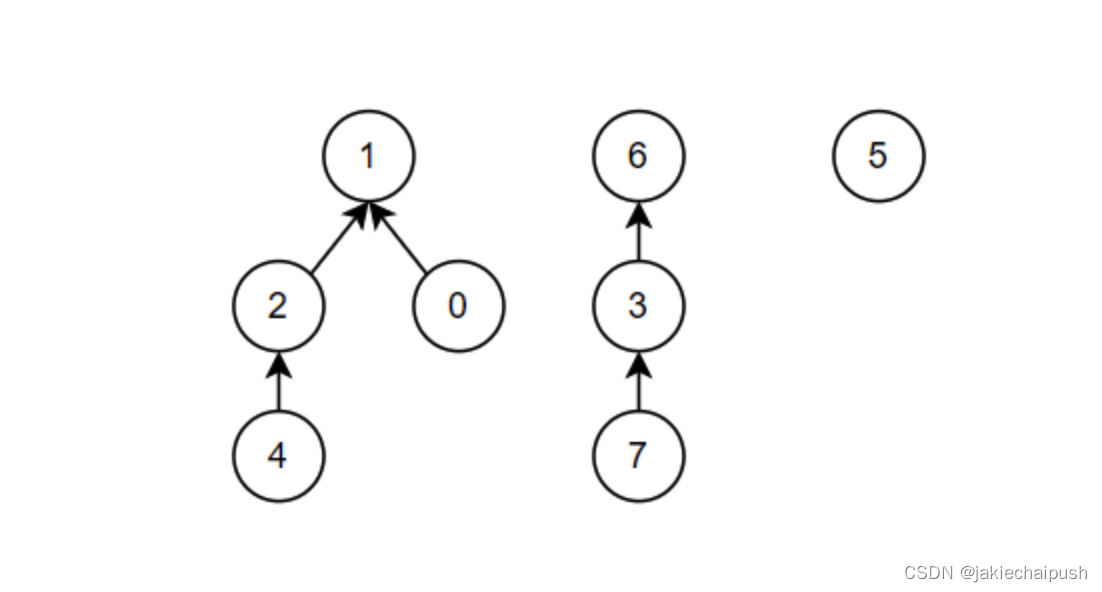
3. find()函数的定义与实现

前面在介绍原理的时候说到，并查集的基本思想是将元素分组，每个组称为一个集合，最终目的是实现高效地判断两个元素是否在同一个集合中。而find函数的作用就是判断一个元素是否属于一个组，而所谓的一组实际上就是一棵树。那么find函数是如何实现判断一个元素是否属于一个组的？原理其实很简单，其实每个组都会有个代表元（这个代表元通常是更节点），只要两个元素拥有共同的代表元它们就属于同一个组。下面我们基于代码分析一下，find函数的原理：

public int find(int x) {
    while (parent[x] != x) {
        x = parent[x];
    }
    return x;
}

在该实现中，我们使用一个while循环来一直向上查找，直到找到该元素所在组的根节点为止。在查找的过程中，我们每次都将当前元素的父节点（parent[x])作为下一个元素进行查找。当找到根节点时，循环终止，返回该节点即可。然而，当并查集的规模比较大时，这种实现的时间复杂度会很高，为$O(n)$，其中$n$是并查集中元素的总数。而优化后的实现可以将时间复杂度降低到$O(\alpha (n))$，其中$\alpha$是阿克曼函数的反函数，可以认为它是一个极小的值，因此可以近似地看作是常数时间复杂度。因此，路径压缩优化对于并查集的性能提升非常显著。

4. 并查集的join函数

并查集（Union-Find Set）中的 join() 函数用于将两个元素所在的组合并成一个大组，它的实现原理很简单，即将其中一个元素的根节点指向另一个元素的根节点即可。具体来说，它的实现可以分为以下两个步骤：

• 找到两个元素所在组的根节点。我们可以使用并查集中的 find() 函数来查找两个元素所在组的根节点。如果它们的根节点相同，则说明它们已经在同一个组中，不需要再合并了。

• 合并两个组。如果两个元素不在同一个组中，则需要将它们所在的组合并成一个大组。具体来说，我们可以将其中一个元素的根节点指向另一个元素的根节点，从而将两个组合并成一个大组。

以下是并查集中 join() 函数的 Java 代码实现：

public void join(int x, int y) {
    int rootX = find(x);
    int rootY = find(y);
    if (rootX != rootY) {
        parent[rootX] = rootY;
    }
}

其中，parent 是一个数组，用于存储每个元素所在组的根节点。初始时，每个元素的父节点都是它自己，即 parent[i] = i。在 join() 函数中，我们首先使用 find() 函数来找到 x 和 y 所在组的根节点。如果它们的根节点相同，说明它们已经在同一个组中，不需要再合并了。如果它们的根节点不同，说明它们不在同一个组中，需要将它们所在的组合并成一个大组。为了实现这一点，我们将其中一个元素的根节点指向另一个元素的根节点即可，这里我们选择将 x 所在组的根节点 rootX 指向 y 所在组的根节点 rootY。具体来说，我们可以将 parent[rootX] 的值赋为 rootY，从而将 x 所在组的所有元素的根节点都指向 y 所在组的根节点 rootY，从而将两个组合并成一个大组。需要注意的是，这里的 join() 函数只是简单地将其中一个元素的根节点指向另一个元素的根节点，并不考虑各组的大小和深度等因素，因此可能会导致并查集出现深度不平衡的情况。针对这个问题，可以使用一些其他的优化策略，例如按秩合并和路径压缩等，以提高并查集的性能和稳定性。

5. 路径压缩优化算法-优化find

前面我们说到，原始的find函数的查找根节点的时间复杂度较高，这里我们考虑将其进行优化。路径压缩是并查集中一种常用的优化技术，它通过修改树的结构来减少后续查找所需经过的节点数量，从而提高并查集的性能。在并查集中，每个元素都有一个父节点，用于表示它所在的组的根节点。当我们查找一个元素所在的组时，实际上就是在不断向上查找该元素的父节点，直到找到根节点为止。路径压缩就是在这个查找的过程中，将沿途经过的所有节点的父节点直接指向根节点，从而降低后续查找所需经过的节点数量。

具体来说，路径压缩的原理可以分为两个步骤：

• 查找根节点：我们首先使用递归调用的方式，不断查找当前元素的父节点，直到找到根节点为止。在查找过程中，如果当前元素的父节点不是根节点，那么我们就将其父节点设置为下一次查找的元素。

• 路径压缩：当我们找到根节点后，就会得到整个树的结构。此时，为了减少后续查找所需经过的节点数量，我们可以将沿途经过的所有节点的父节点都直接指向根节点。这个过程可以在递归调用的返回过程中完成，具体来说就是在返回前将当前元素的父节点设置为根节点即可。

以下是基于路径压缩优化的并查集中find()函数的Java实现：

public int find(int x) {
    if (parent[x] != x) {
        parent[x] = find(parent[x]); // 路径压缩
    }
    return parent[x];
}

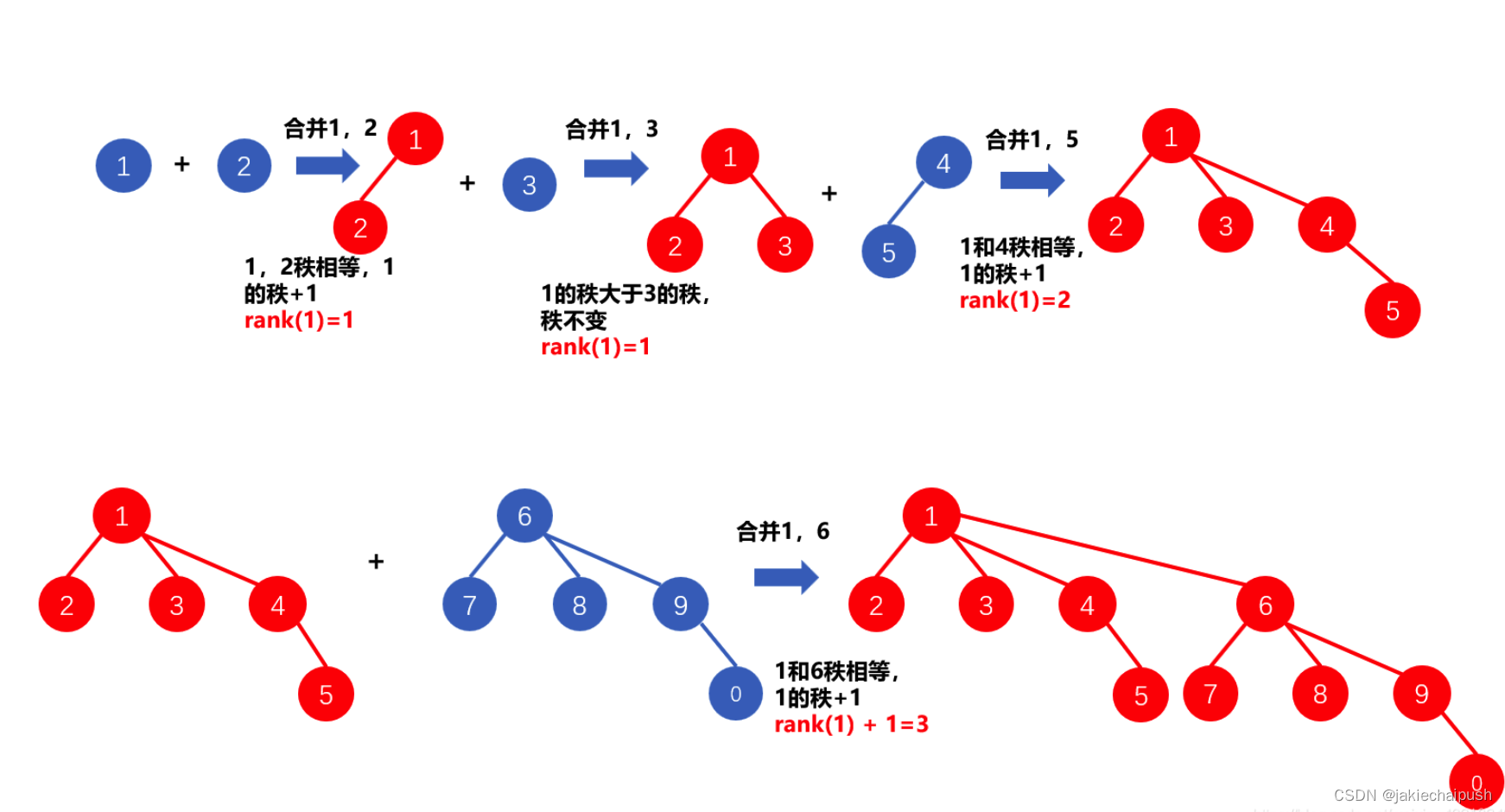
6. 路径压缩优化算法+按秩合并算法

路径压缩算法还可以与按秩合并算法结合起来，以进一步提高并查集的性能和稳定性。具体来说，可以在每个节点上增加一个权值，表示该节点所在组的大小或深度等信息，从而实现按秩合并算法的功能。在进行路径压缩的同时，还可以更新节点的权值信息，从而保证并查集的平衡性和稳定性。在路径压缩算法中，为了避免对并查集中所有节点都进行路径压缩操作，可能会出现一些节点的父节点指向了自己的情况。为了避免这种情况，可以在进行路径压缩时，同时对节点进行加权标记，表示该节点已经进行了路径压缩操作。具体来说，可以在 find() 函数中增加一个参数 compress，表示是否进行路径压缩，同时在每个节点上增加一个标记 compressed，表示该节点是否已经进行了路径压缩。修改后的 find() 函数实现如下：

public int find(int x, boolean compress) {
    if (parent[x] != x) {
        if (compress && !compressed[x]) {
            // 路径压缩，并更新节点的权值信息
            parent[x] = find(parent[x], compress);
            size[x] = size[parent[x]];
            compressed[x] = true;
        } else {
            // 递归查找根节点
            parent[x] = find(parent[x], compress);
        }
    }
    return parent[x];
}