目录

前言

1.系统描述

2.控制器设计

3.模糊推理估计不确定f

3.1构造模糊系统

3.2模糊推理过程

3.3 自适应律设计

4.仿真分析

4.1仿真模型

4.2仿真结果

5.总结

---

前言

在一般的建模仿真中，我们假设模型都是可以用数学模型描述出来的是确定的，称为理想系统。但是在实际中，系统大都是不确定的，得到我们更接近实际的系统，称为名义系统或者标称系统，如果能对于不确定项进行较为精准的估计，再利用对逼近的系统进行控制器设计，那么我们的实际系统在这样的控制器下将实现更佳的性能水准，从上篇文章利用模糊控制估计不确定扰动用于实现自适应变切换增益，有效降低滑膜控制的抖振问题，证实了模糊理论具有万能逼近特性，链接如下：

VSC/SMC(十五)——基于模糊逼近的积分滑模控制_Mr. 邹的博客-CSDN博客_积分滑模面的优势

本文再次利用模糊控制理论逼近系统的不确定项，为控制器设计自适应律，实现一种简单的自适应滑膜控制。

1.系统描述

其中，f和g均为有界不确定项，dt为扰动。

2.控制器设计

定义误差变量e=x-xd，为上述系统设计一种简单的滑模面：

有了前面滑膜理论的基础，采用等速趋近律，很容易得到控制律：

但是f和g此时是未知的，也就是控制器直接无法实现，所以必须要得到一个近似估计的f^和g^，由于方法类似，这里为了简化假设g已知，只需要估计f，所以下面利用模糊推理对f进行估计。

3.模糊推理估计不确定f

3.1构造模糊系统

①分别为x1和x2设计5个模糊集，分别为μ1和μ2

②采用如下模糊规则：

 设计25条上述模糊规则构造模糊系统逼近f。

3.2模糊推理过程

①利用乘机推理实现规则的前提推理

②利用模糊器求出隶属度函数对应的f大小

③结合①和②得到推理结果，并对模糊规则进行运算，得到模糊系统的输出

④利用平均解模糊器得到f的估计值f^：

 其中：θ^为自由参数，也是自适应律的状态变量；ξ为5*5=25维的模糊基向量，第l1l2个元素为：

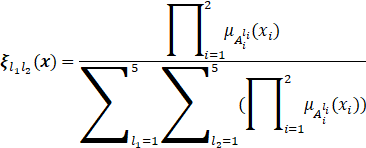
3.3 自适应律设计

设估计f对应的最优参数θ*为：

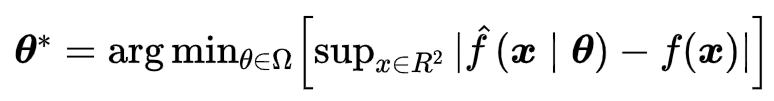
得到逼近的f^:

其中ε为逼近误差。

定义如下形式的Lyapunov函数：

其中

求导有：

此时上述系统控制律为：

 将控制律代入V'，有：

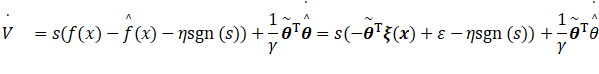
取η>|ε|max，得到自适应律：

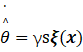
​​​​​​​4.仿真分析

为了简化我们直接在这里定义g=1，则上述二阶系统为：

 相应的滑膜控制律为：

 其中：

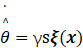
4.1仿真模型

xd=sin(t)，dt为随机白噪声。

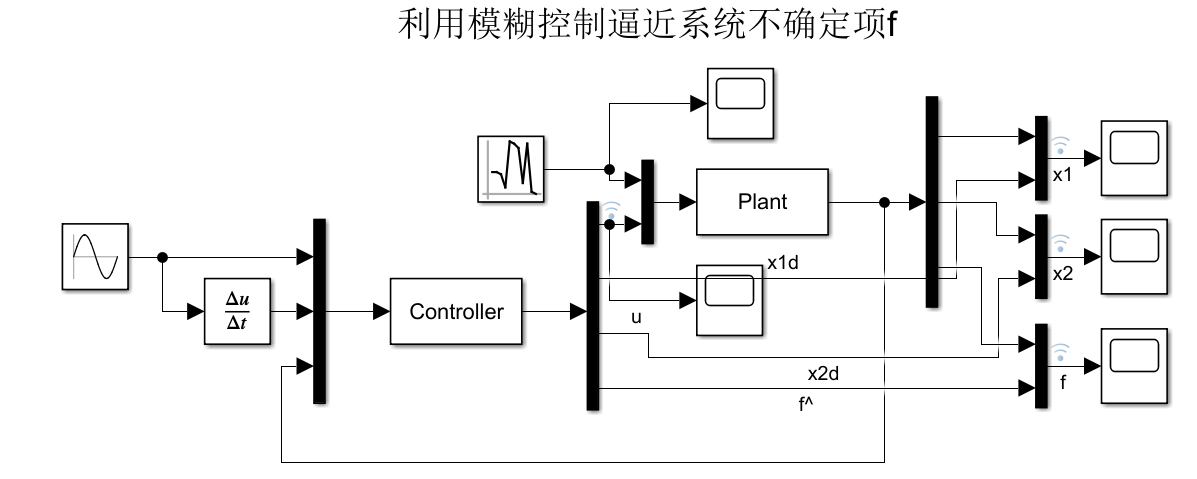
4.2仿真结果

γ=5000

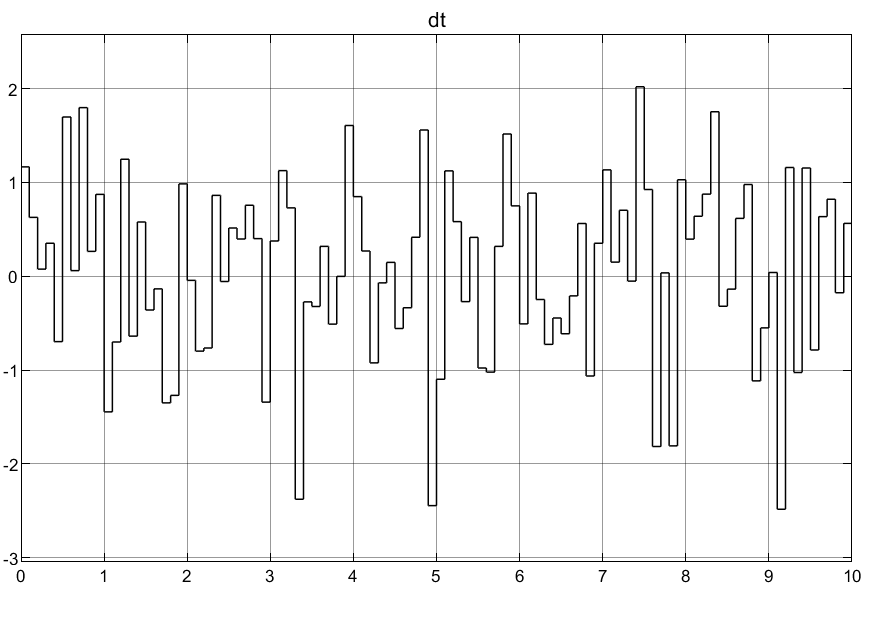
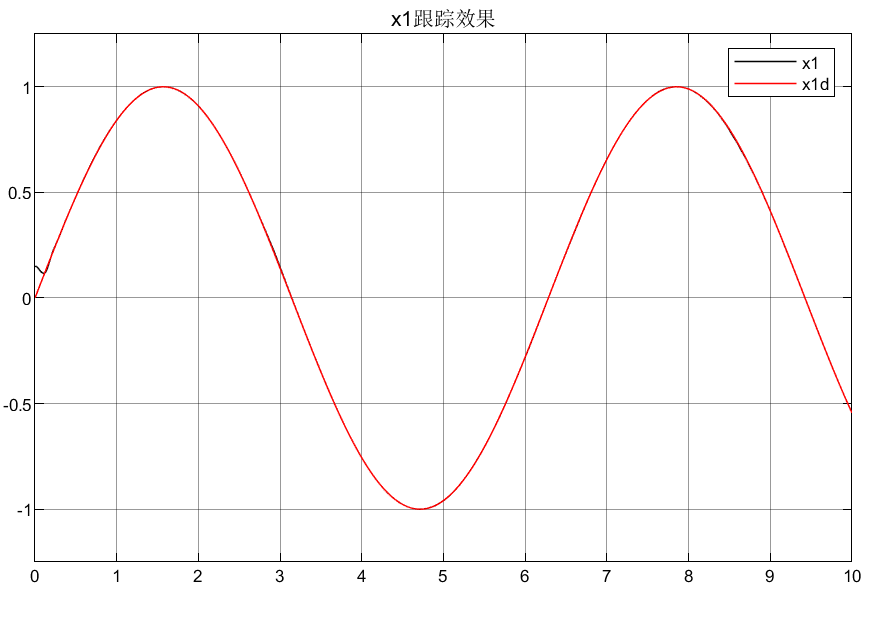
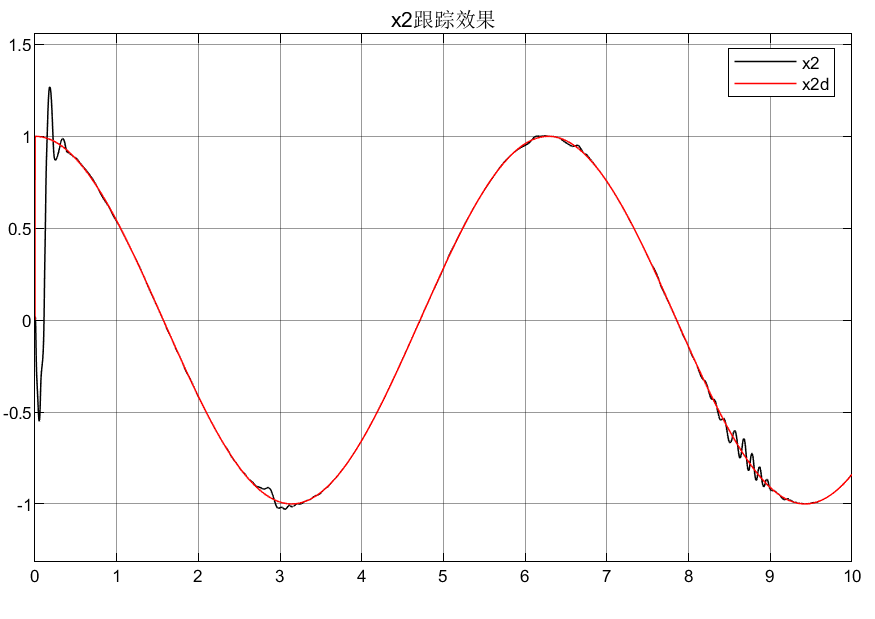
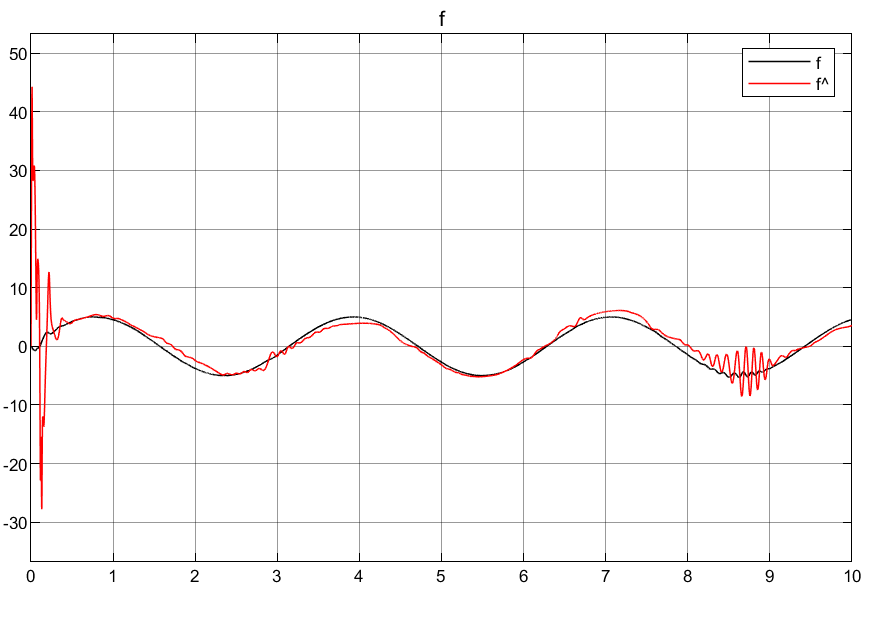
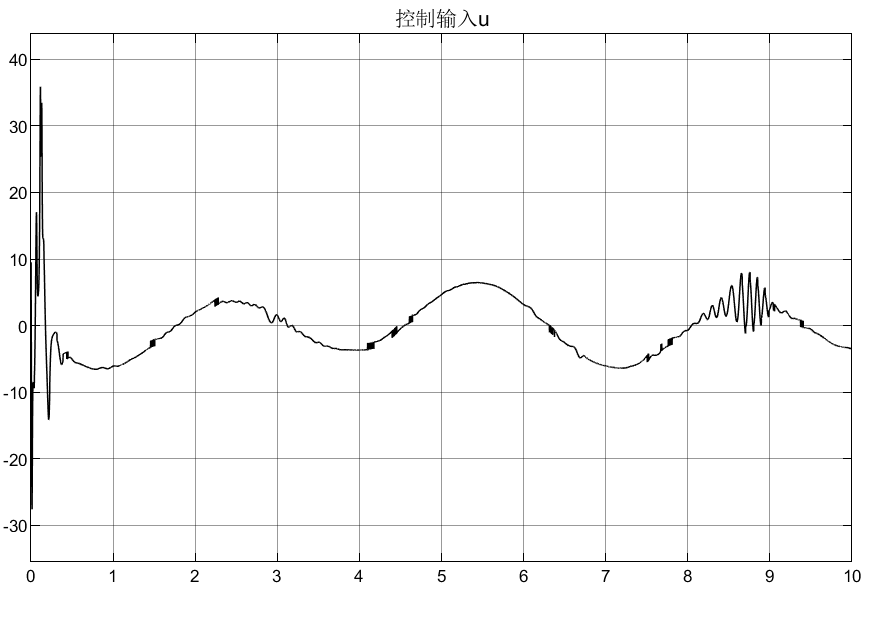
γ取值大一点误差估计更加准确，如下第一行图像结果为γ=2000是x'的跟踪效果和f的估计效果，第二行为γ=200取值效果对比：

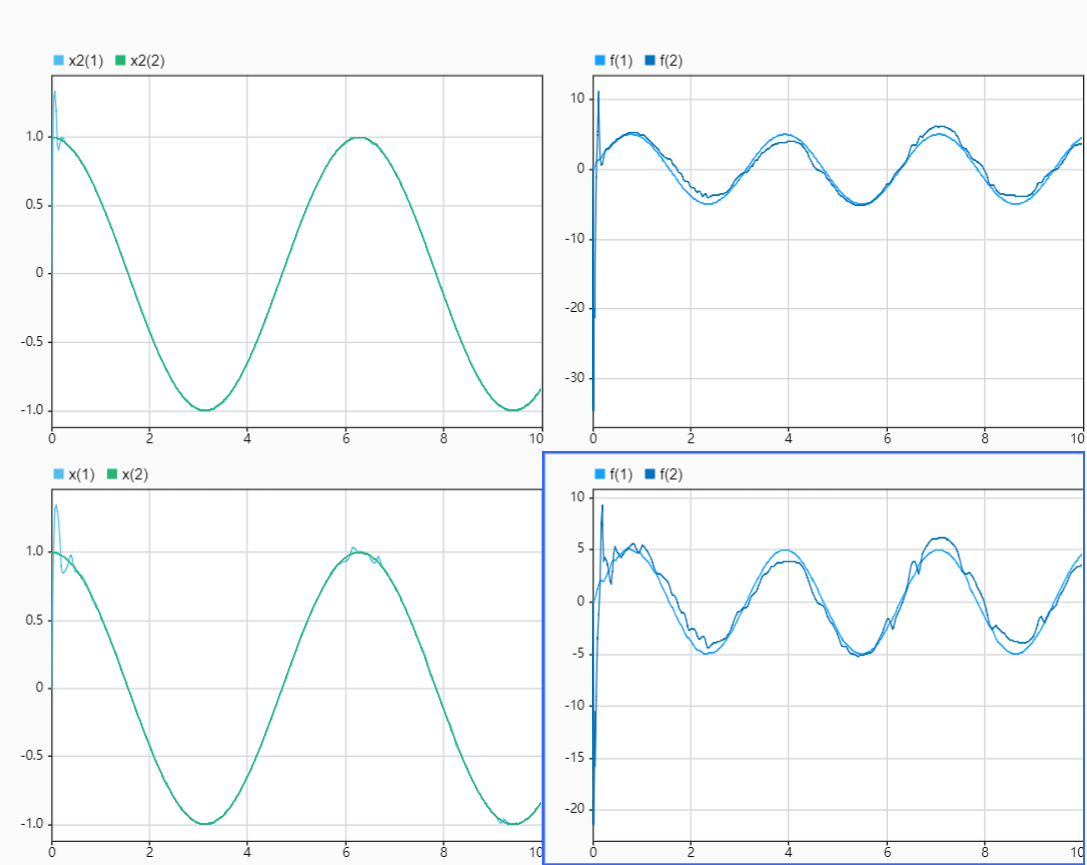
5.总结

①使用模糊逼近估计不确定项f，从而实现对实际系统更加精准的估计，并且在外部扰动下，系统能保持良好的跟踪效果，证实了基于模糊控制逼近不确定项的滑膜控制算法有效性。

②本文中γ取值大一些估计精度更高，但是会导致初始峰值变大。

③本文选择的是gaussmf(x,[pi/12,[-pi/3;-pi/6;0;pi/6;pi/3]])隶属度函数，而且发现隶属度函数的选择以及隶属度函数的参数对估计的影响很大！

前面的文章也使用观测器进行对扰动的估计，读者可以自行体会，链接：

VSC/SMC（七）——基于高增益观测器的滑模控制(含程序模型)_Mr. 邹的博客-CSDN博客_滑膜观测器c语言代码

VSC/SMC（八）——基于慢时变干扰观测器的滑模控制(含程序模型)_Mr. 邹的博客-CSDN博客_慢时变

基于扩张观测器(LESO)的滑模控制_Mr. 邹的博客-CSDN博客_leso观测器