1.题目链接：

40. 组合总和 II

2.解题思路：

树层：同层遍历

树枝：递归遍历

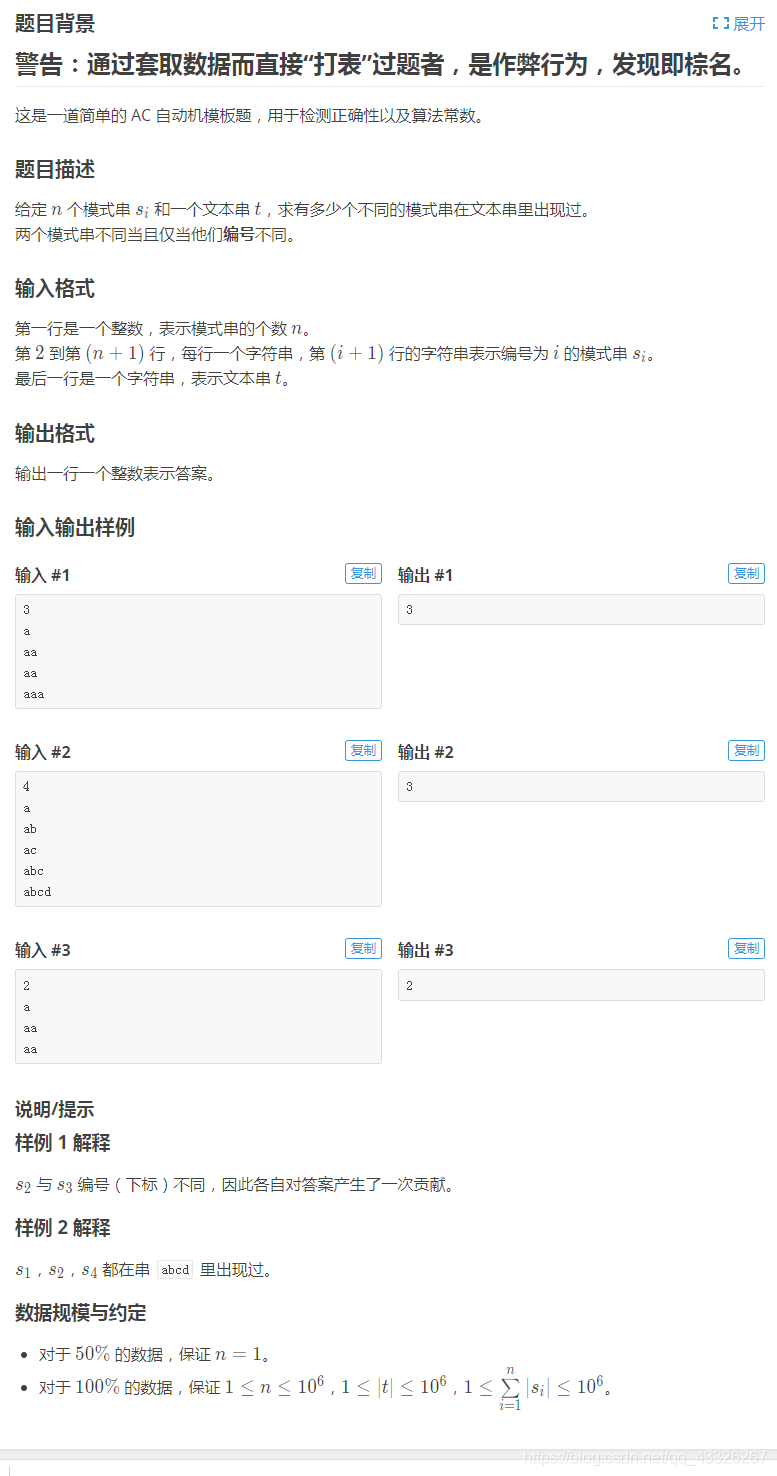
2.1.题目要求：

给定一个数组 candidates 和一个目标数 target ，找出 candidates 中所有可以使数字和为 target 的组合。

candidates 中的每个数字在每个组合中只能使用一次。

注意：解集不能包含重复的组合。

示例：输入: candidates = [2,5,2,1,2], target = 5, 所求解集为: [ [1,2,2], [5] ]

2.2.思路：

这也是构造一颗n叉树，for循环里面套递归，不过这里题目的要求有变化，

输入的数组 candidates 的每一个数字只能用一次，但是数组里又有重复值的元素。

比如 [2,5,2,1,2]的输出[1,2,2]，里面的两个 2 用了 [2,5,2,1,2] 里的随机两个，是满足题目的定义的

而且要求输出的组合不能重复

比如：组合（1，2，2）再输出一个（1，2，2）或者（2，2，1）是不行的。

在这个条件怎么让输出的组合不重复？（去重操作）

去重的是同一树层上的“使用过”的数字，同一树枝上的都是一个组合里的元素，不用去重

总体思路就是：

在 “构造一颗n叉树，for循环里面套递归” 的基础上，加上去重操作

流程如图：

2.3.回溯三部曲：

先给数组排个序，用于剪枝和数层去重判断。

2.3.1.确定回溯函数参数

用used数组来去重（后面说明）

vector<vector<int>> result; // 存放组合集合
vector<int> path;           // 符合条件的组合
void backtracking(vector<int>& candidates, int target, int sum, int startIndex,
 vector<bool>& used) {

2.3.2.确定终止条件

这里sum > target ，在剪枝的时候会去掉（剪枝的时候说明）

if (sum > target) { // 这个条件其实可以省略
    return;
}
if (sum == target) {
    result.push_back(path);
    return;
}

2.3.3.确定单层遍历逻辑

1.used的目的是跳过同一树层使用过的元素，怎么操作的？（数组已排序）

利用数组 candidates [ i ] 和 [ i-1 ] 的关系，判断前后是否是重复的数字，

然后由usd的值对其 [ i-1 ] 进行判断（i-1是当前树枝的上一层），used到了一个树枝的时候其对应的used[ i ]就会变成 1 ，回溯的时候变成 0 。

2.used判断的依据是：

当进行树枝搜索的时候，其上面一层used的 [ i-1 ] 永远是 1，

而进行树层搜索的时候，其上面一层的used [ i-1 ] 永远是 0。（只有它本层的use [i] = 1 ）

这样的话，

当遇见candidates 的 [ i ] 等于 [ i-1 ] 的时候，用used [ i-1 ] 判断其是树层还是树枝，再做相应的去重操作就好了

3.流程如图：

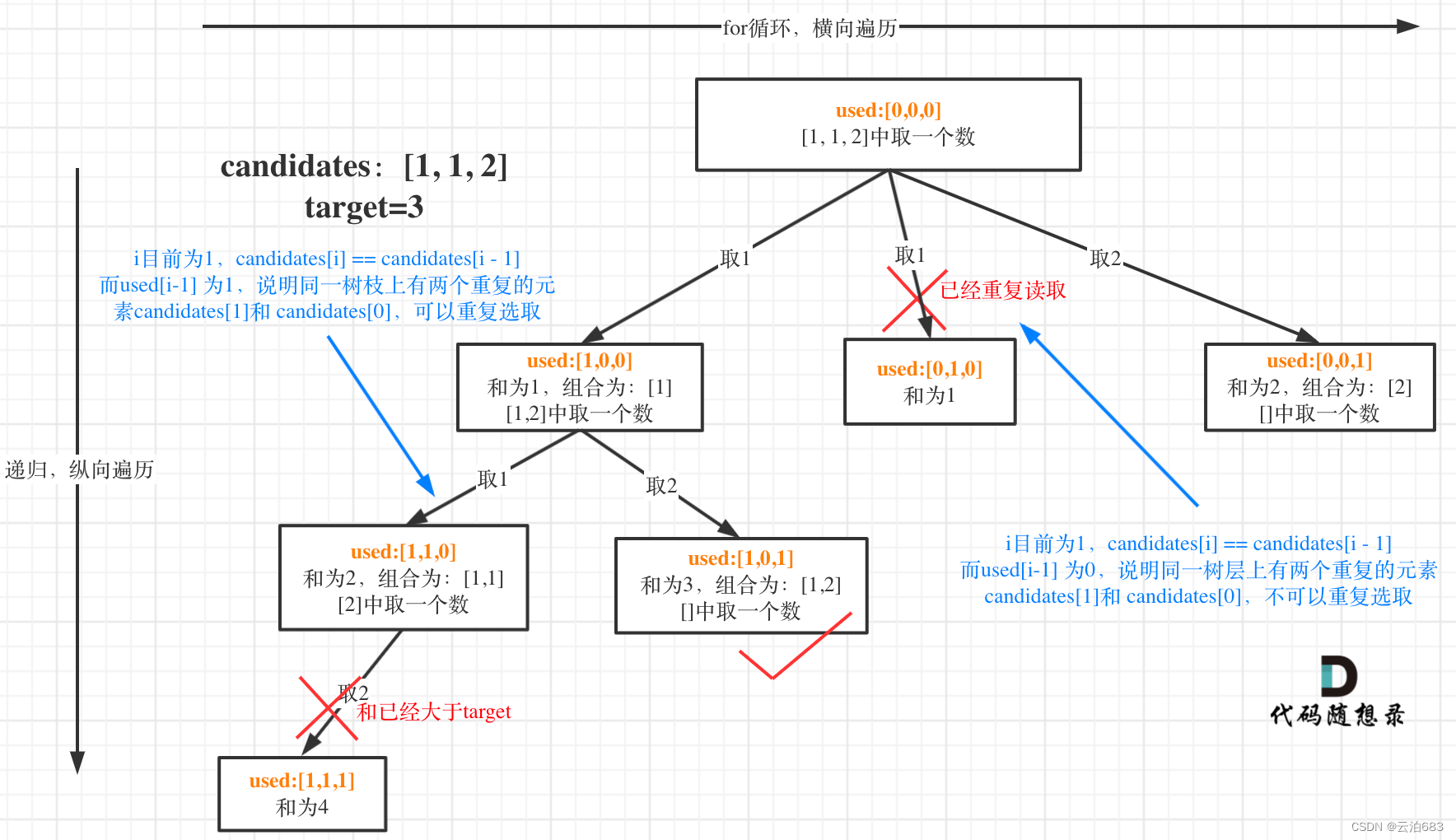
4.used代码中对应的大概操作：

    // 用于终止条件，对同一树层使用过的元素进行跳过
    if (i > 0 && candidates[i] == candidates[i - 1] && used[i - 1] == false) continue;
    //用于for循环，添加递归一层为1，回溯一层为0的逻辑
    for(){
    used[i] = true;
    backtracking(candidates, target, sum, i + 1, used);//做隔开
    used[i] = false;
    }

5.完整片段代码：

for (int i = startIndex; i < candidates.size() && sum + candidates[i] <= target; i++) {
    // used[i - 1] == true，说明同一树枝candidates[i - 1]使用过
    // used[i - 1] == false，说明同一树层candidates[i - 1]使用过
    // 要对同一树层使用过的元素进行跳过
    if (i > 0 && candidates[i] == candidates[i - 1] && used[i - 1] == false) {
        continue;
    }
    sum += candidates[i];
    path.push_back(candidates[i]);
    used[i] = true;
    backtracking(candidates, target, sum, i + 1, used);
    // 和39.组合总和的区别1：这里是i+1，每个数字在每个组合中只能使用一次
    used[i] = false;
    sum -= candidates[i];
    path.pop_back();
}

2.4. 总代码：

class Solution {
private:
    vector<vector<int>> result;
    vector<int> path;
    void backtracking(vector<int>& candidates, int target, int sum, int startIndex, vector<bool>& used) {
        if (sum == target) {
            result.push_back(path);
            return;
        }
        for (int i = startIndex; i < candidates.size() && sum + candidates[i] <= target; i++) {
            // used[i - 1] == true，说明同一树枝candidates[i - 1]使用过
            // used[i - 1] == false，说明同一树层candidates[i - 1]使用过
            // 要对同一树层使用过的元素进行跳过
            if (i > 0 && candidates[i] == candidates[i - 1] && used[i - 1] == false) {
                continue;
            }
            sum += candidates[i];
            path.push_back(candidates[i]);
            used[i] = true;
            backtracking(candidates, target, sum, i + 1, used); // 和39.组合总和的区别1，这里是i+1，每个数字在每个组合中只能使用一次
            used[i] = false;
            sum -= candidates[i];
            path.pop_back();
        }
    }

public:
    vector<vector<int>> combinationSum2(vector<int>& candidates, int target) {
        vector<bool> used(candidates.size(), false);
        path.clear();
        result.clear();
        // 首先把给candidates排序，让其相同的元素都挨在一起。
        sort(candidates.begin(), candidates.end());
        backtracking(candidates, target, 0, 0, used);
        return result;
    }
};