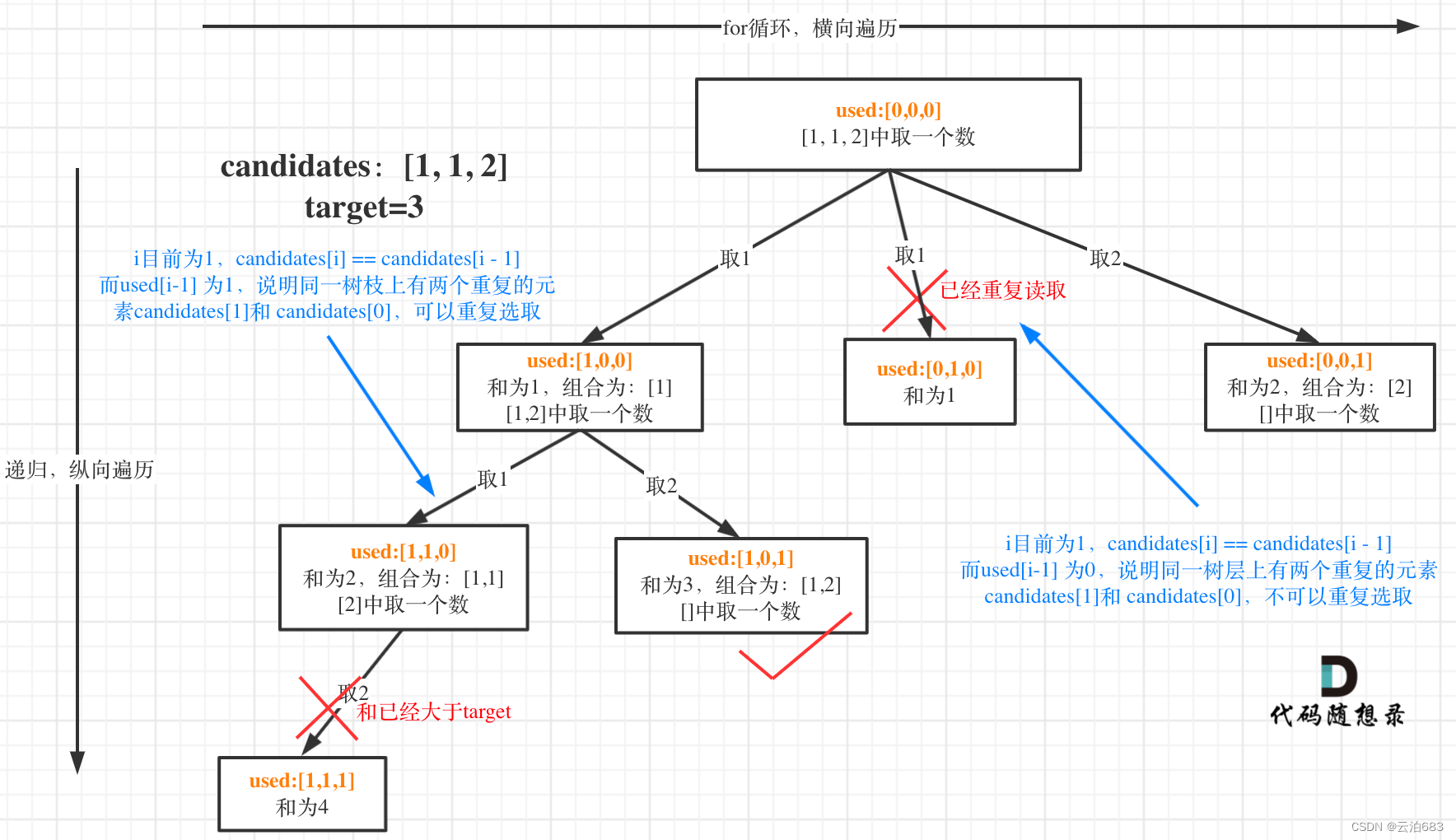
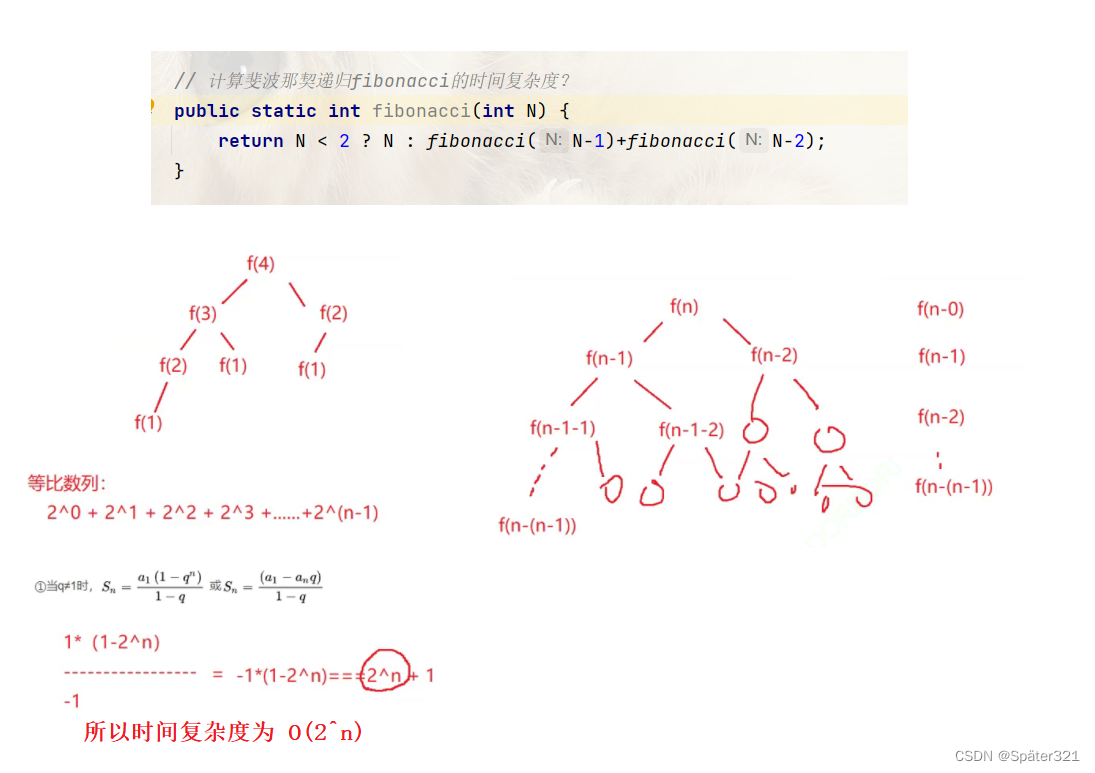
1.普通树
A为整个树的根节点。而B,C,D可以看做子树的根节点,在下面分别长出三棵子树。
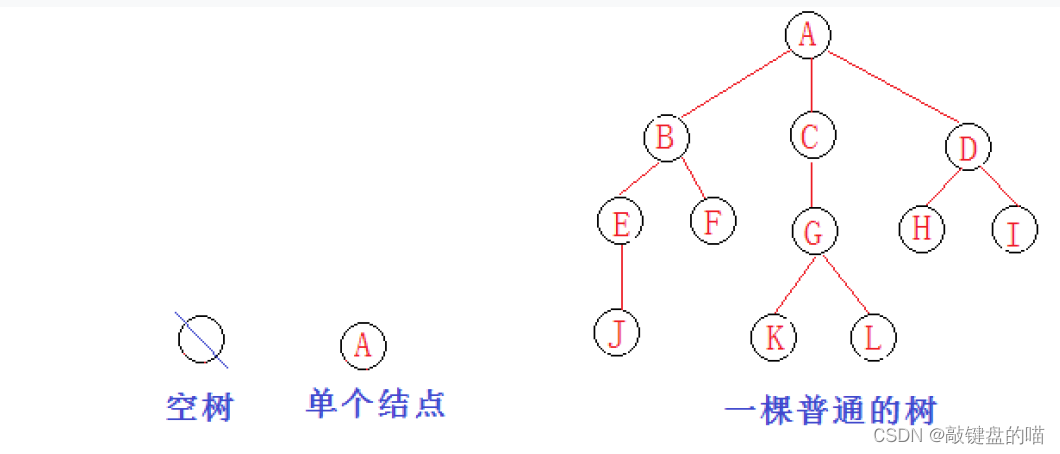
二、二叉树概念及结构
1.概念
一棵二叉树是结点的一个有限集合,该集合或者为空,或者是由一个根节点加上两棵别称为左子树和右子树的二叉树组成。
二叉树的特点:
- 如果它的左子树非空,则左子树中的所有结点的值都小于根节点的值
- 反之,若右子树非空,则右子树上所有的结点的值都大于等于根节点的值
- 其左右子树本身也是二叉排序树
- 二叉树的子树有左右之分,且左右不能颠倒。
- 每个节点最多有两棵子树,即不存在超过度为2的节点。

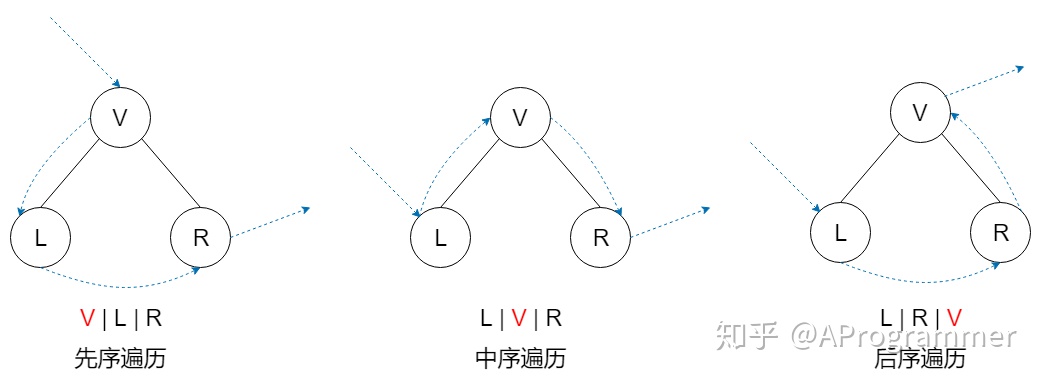
一、顺序存储
优点:读取某个指定的节点的时候效率比较高O(0)
缺点:会浪费空间(在非完全二叉树的时候)
二、链式存储
优点:读取某个指定节点的时候效率偏低O(nlogn)
缺点:相对二叉树比较大的时候浪费空间较少
二叉树的顺序存储,寻找后代节点和祖先节点都非常方便,但对于普通的二叉树,顺序存储浪费大量的存储空间,同样也不利于节点的插入和删除。因此顺序存储一般用于存储完全二叉树。
链式存储相对顺序存储节省存储空间,插入删除节点时只需修改指针,但寻找指定节点时很不方便。不过普通的二叉树一般是用链式存储结构。
【顺序存储】
查找速度快
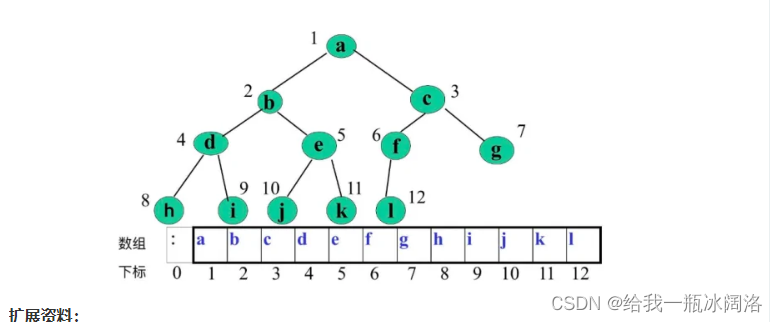
三、特殊的二叉树
1. 满二叉树:一个二叉树,如果每一个层的结点数都达到最大值,则这个二叉树就是满二叉树。也就是说,如果一个二叉树的层数为K,且结点总数是(2^k) -1 ,则它就是满二叉树。
2、完全二叉树:完全二叉树是由满二叉树引出的。满二叉树要求每一层的节点数都达到最大值,完全二叉树仅要求除最后一层外的节点数达到最大值,也就是说最后一层可以不满。我们可以把满二叉树看错特殊的完全二叉树。

四,二叉排序树
二叉排序树也叫二叉查找树、二叉搜索树,既然名字都不一般,那它显然和普通的二叉树不同。那到底有什么不同,它的特点或者优点在哪里呢?不妨,我们来构建一棵二叉树。
1,二分搜索树的优缺点
(1)⭐优势⭐
查找元素、插入元素、删除元素的时间复杂度都是O(logn)。还可以方便的回答很多数据之间关系的问题:min,max,floor,ceil,rank,select
(2)⭐局限性⭐
当将一组数据以近乎有序的顺序插入空二分搜索树中时,几乎每一个节点都是父节点的右孩子,二分搜索树近乎退化成了一个链表,相关算法时间复杂度都退化成了O(N)。因此有了平衡二叉树,不会退化成链表,如:红黑树等。
构建二叉排序树

中序遍历后

二叉排序树查找

删除节点


五,平衡二叉树
什么是平衡二叉树(AVL) - 知乎
平衡二叉树,又称AVL树,用于解决二叉排序树高度不确定的情况,如果二叉排序树的子树间的高度相差太大,就会让二叉排序树操作的时间复杂度升级为O(n),为了避免这一情况,为最坏的情况做准备,就出现了平衡二叉树,使树的高度尽可能的小,其本质还是一棵二叉搜索树。
平衡二叉树的性质:
- 每个节点最多只有两个子节点(二叉)
- 规则2:每个节点的值比它的左子树所有的节点大,比它的右子树所有节点小(有序)
左子树和右子树的高度之差的绝对值小于等于1
左子树和右子树也是平衡二叉树
为了方便起见,给树上的每个结点附加一个数字,给出该结点左子树与右子树的高度差,这个数字称为结点的平衡因子(BF)
平衡二叉树的目的是为了减少二叉查找树层次,提高查找速度。
平衡二叉树或为空树,或为如下性质的二叉排序树:
(1)左右子树深度之差的绝对值不超过1;
(2)左右子树仍然为平衡二叉树.

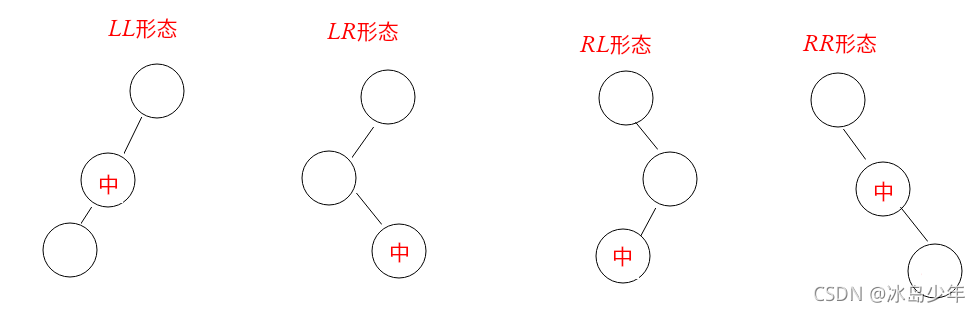
二叉树失衡的四种状态
左子树与右子树高度差的绝对值小于或等于1
例如图 2.1 不是平衡二叉树,因为结点 60 的左子树不是平衡二叉树。

图 2.2 也不是平衡二叉树,因为虽然任何一个结点的左子树与右子树都是平衡二叉树,但高度之差已经超过 1 。

图 2.3 不是平衡二叉树

AVL树插入时的失衡与调整
图 5.1 是一颗平衡二叉树在此平衡二叉树插入节点 99 ,树结构变为:

在此平衡二叉树插入节点 99 ,树结构变为:
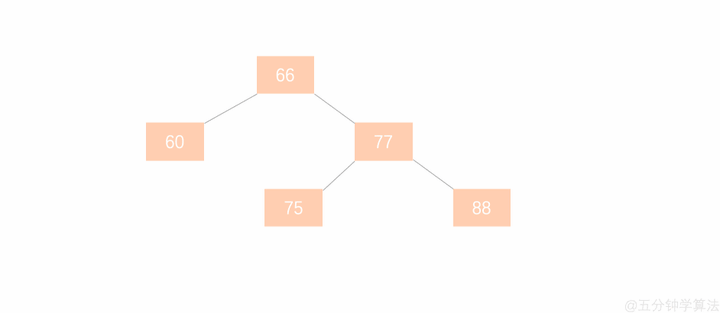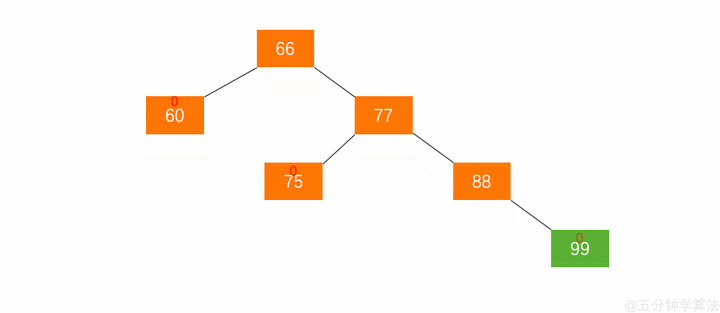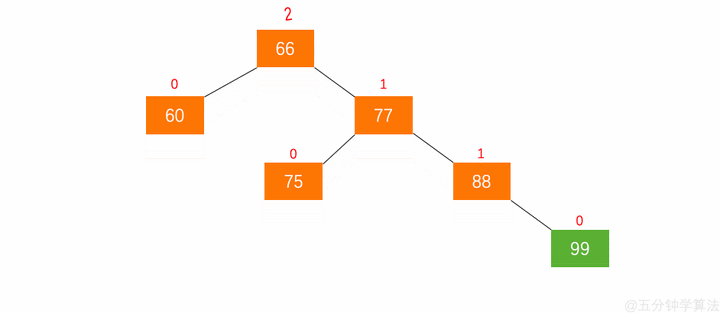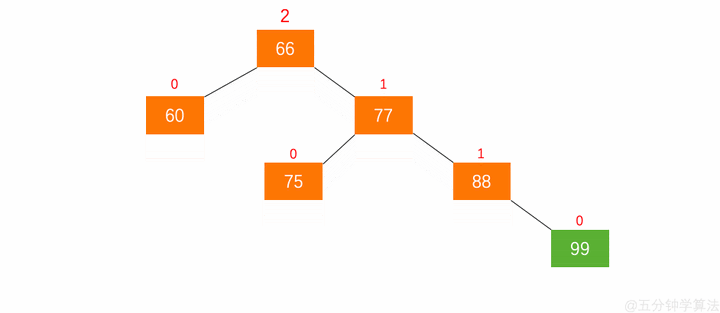
在动图 5.2 中,节点 66 的左子树高度为 1,右子树高度为 3,此时平衡因子为 -2,树失去平衡。
在动图 5.2 中,以节点 66 为父节点的那颗树就称为 最小失衡子树。
最小失衡子树:在新插入的结点向上查找,以第一个平衡因子的绝对值超过 1 的结点为根的子树称为最小不平衡子树。也就是说,一棵失衡的树,是有可能有多棵子树同时失衡的。而这个时候,我们只要调整最小的不平衡子树,就能够将不平衡的树调整为平衡的树。
平衡二叉树的失衡调整主要是通过旋转最小失衡子树来实现的。根据旋转的方向有两种处理方式,左旋 与 右旋 。
旋转的目的就是减少高度,通过降低整棵树的高度来平衡。哪边的树高,就把那边的树向上旋转
红黑树
红黑树的规则:
- 性质1:每个节点要么是红色,要么是黑色。
- 性质2:根节点永远是黑色的。
- 性质3:所有的叶子节点都是空节点(即null),并且是黑色的。
- 性质4:每个红色节点的两个子节点都是黑色。(从每个叶子到根的路径上不会有两个连续的红色节点。)
- 性质5:从任一节点到其子树中每个叶子节点的路径都包含相同数量的黑色节点。
平衡二叉树和红黑树的区别
- 平衡二叉树的左右子树的高度差绝对值不超过1,但是红黑树在某些时刻可能会超过1,只要符合红黑树的五个条件即可。
- 二叉树只要不平衡就会进行旋转,而红黑树不符合规则时,有些情况只用改变颜色不用旋转,就能达到平衡