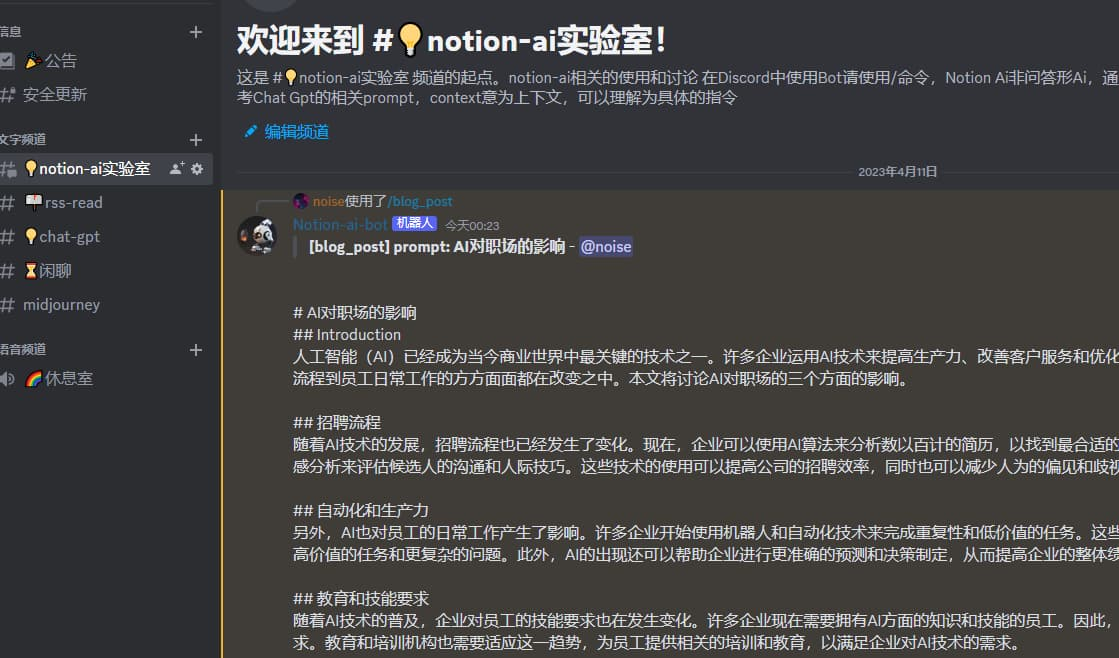
G. Hits Different

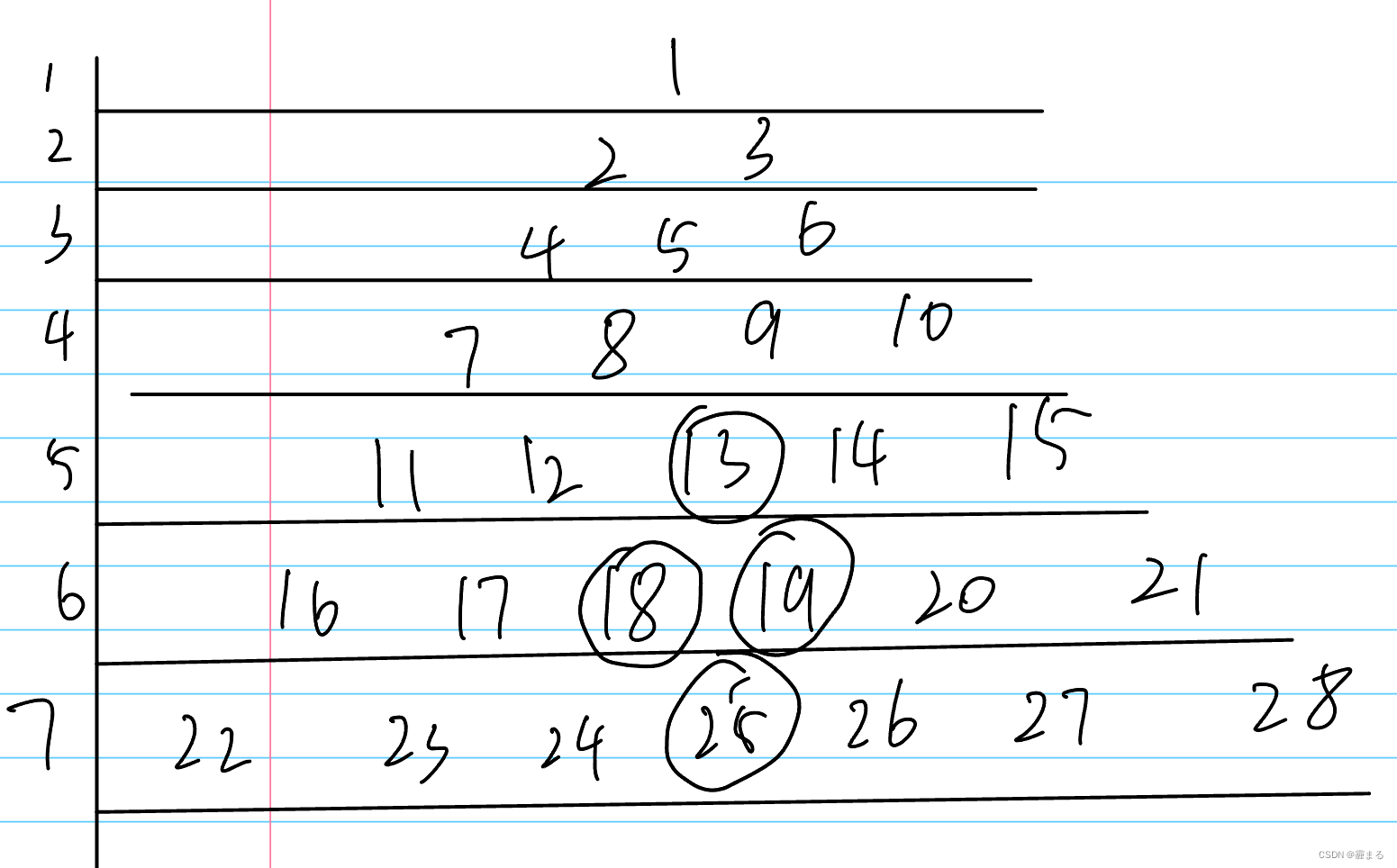
记dp数组为答案数组
首先

dp[2]=$2^2$+$1^2$
dp[3]=$3^2$+$1^2$
dp[5]=$2^2$+$3^2$+$1^2$
不难发现dp[5]=dp[2]+dp[3]-dp[1]
同理dp[25]=dp[18]+dp[19]-dp[13]

接下来就是愉快的找公式时间
观察到题目中给的每一层塔的级数 (易得级数公式为$\frac{n\ast (n+1}{2}$)
找到当前数字x所对应的级数为$pos$, 此时$x-pos$就是这个数字头上左边的数字, 易得$x-pos+1$就是头上右边的数
同理可得$x-pos+1$头上左边的数字就是$x-2\ast pos+2$
所以公式就是$x\ast x+dp[x-pos]+dp[x-pos+1]+dp[x-2\ast pos+2]$

但是! 公式并不完全适用
此公式不适用于左右两端的情况

数字在金字塔左端时, 级数计算调整-1(至于为什么调整可以自己找找看), 且不能加左上方的数(不存在这个位置的数字), 也不需要减去重复的值, 因为重复的值是在加了两项dp值后产生的, 此时不存在这个位置的数因此也不需要减去重复的值
数字在金字塔右端时, 级数正常计算, 其他同上

明白了公式后, 仍然有一个难题在面前, 那就是如何找到这个数所在的金字塔层数

其实很简单: 只需要预处理出来所有1e6以下的级数($\frac{n\ast (n+1}{2}$), 在查找时候进行lower_bound二分即可

代码

#include<bits/stdc++.h>
using namespace std;
#define ll long long
#define endl "\n"

ll cnt,n,m,t,ans,ant;
const int N=1e6+10;
const int INF=0x3f3f3f3f;
const ll llINF=0x3f3f3f3f3f3f3f3f;
ll arr[N];
string str;
vector<ll>vis(N);
vector<ll>ks;

ll dfs(ll x)
{
    if(x<=0) return 0;
    if(x==0) return 0;
    if(vis[x]) return vis[x];
    ll pos=0;

    pos=lower_bound(ks.begin(),ks.end(),x)-ks.begin();

    ll fuck=pos*(pos+1)>>1;
    if(x==fuck)
    {
        vis[x]+=x*x+dfs(x-pos);
        return vis[x];
    }
    if(x==fuck-pos+1)
    {
        pos--;
        vis[x]+=x*x+dfs(x-pos);
        return vis[x];
    }
    vis[x]+=x*x+dfs(x-pos)+dfs(x-pos+1)-dfs(x-2*pos+2);
    return vis[x];
}

void solve()
{
    cin>>n;
    cout<<dfs(n)<<endl;
    return;
}

int main()
{
    ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);
    //所有输入用cin
    //所有输出用cout
	vis[1]=1;
    vis[2]=5;
    vis[3]=10;
    ks.push_back(0);
    for(int i=1;i<=1000000;i++)
    {
        cnt=i*(i+1)>>1;
        if(cnt>=1000000) break;
        // cout<<cnt<<endl;
        ks.push_back(cnt);
    }

    cin>>t;
    while(t--)
        solve();
    return 0;
}

记得开longlong